the doctor recommended that Matt increase the number of calories you consume from 2000 to 2800 by what percent did the number of calories increase
Answers
Answer:
40% number of calories have increased
Step-by-step explanation:
Old Value ( Calories consume before) = 2000
New Value (increase in Calories consumed) = 2800
We need to find by what percent did the number of calories increase
To find percent increase, the formula used is:
\(Percent\: increase=\frac{New\:Value-Old\:Value}{Old\:Value}\times 100%\)
Putting values in formula and finding percent increase
\(Percent\: increase=\frac{New\:Value-Old\:Value}{Old\:Value}\times 100\%\:\\Percent\: increase=\frac{2800-2000}{2000}\times 100\%\: \\Percent\: increase=\frac{800}{2000}\times 100\%\: \\Percent\: increase=0.4\times 100\%\: \\Percent\: increase=40\%\)
So, 40% number of calories have increased
Related Questions
Is 604,892 divisible by 4?
Answers
Answer:
yes it is 604892÷4=151,223
Given the rectangle below, write a simplified expression that represents the perimeter and terms of x. Use your expression to solve for x, given that the perimeter is 62.
If you give the wrong answer I will report you

Answers
The expression representing the perimeter is 6x + 39
x = 3. 8
What is the perimeter?The formula for perimeter of a rectangle is given as;
Perimeter = 2 ( length + width)
From the image shown, we have that:
length = 2xwidth = x + 13Now, let's substitute the value
Perimeter = 2 ( 2x + x + 13)
collect like terms
Perimeter = 2 ( 3x + 13)
Expand the bracket
Perimeter = 6x + 39
If perimeter = 62
62 = 6x + 39
6x = 62 - 39
6x = 23
x = 23/ 6
x = 3. 8
Thus, the expression representing the perimeter is 6x + 39
Learn more about perimeter here:
https://brainly.com/question/24571594
#SPJ1
10000 is times as great as what number?
Answers
Answer:
24691861.
Step-by-step explanation:
:)
Use the definition to calculate the derivative of the following function. Then find the values of the derivative as specified.

Answers
Answer:
Refer to the step-by-step explanation, please follow along very carefully. Answers are encased in two boxes.
Step-by-step explanation:
Given the following function, find it's derivative using the definition of derivatives. Evaluate the function when θ=1, 11, and 3/11
\(p(\theta)=\sqrt{11\theta}\)
\(\hrulefill\)
The definition of derivatives states that the derivative of a function at a specific point measures the rate of change of the function at that point. It is defined as the limit of the difference quotient as the change in the input variable approaches zero.
\(f'(x) = \lim_{{h \to 0}} \dfrac{{f(x+h) - f(x)}}{{h}}\)\(\hrulefill\)
To apply the definition of derivatives to this problem, follow these step-by-step instructions:
Step 1: Identify the function: Determine the function for which you want to find the derivative. In out case the function is denoted as p(θ).
\(p(\theta)=\sqrt{11\theta}\)
Step 2: Write the difference quotient: Using the definition of derivatives, write down the difference quotient. The general form of the difference quotient is (f(x+h) - f(x))/h, where "x" is the point at which you want to find the derivative, and "h" represents a small change in the input variable. In our case:
\(p'(\theta) = \lim_{{h \to 0}} \dfrac{{p(\theta+h) - p(\theta)}}{{h}}\\\\\\\Longrightarrow p'(\theta)= \lim_{h \to 0} \dfrac{\sqrt{11(\theta + h)} - \sqrt{11\theta} }{h}\)
Step 3: Take the limit:
We need to rationalize the numerator. Rewriting using radical rules.
\(p'(\theta)= \lim_{h \to 0} \dfrac{\sqrt{11(\theta + h)} - \sqrt{11\theta} }{h} \\\\\\\Longrightarrow p'(\theta)= \lim_{h \to 0} \dfrac{\sqrt{11\theta + 11h} - \sqrt{11\theta} }{h}\\\\\\\Longrightarrow p'(\theta)= \lim_{h \to 0} \dfrac{\sqrt{11}\sqrt{\theta+h} - \sqrt{11}\sqrt{\theta} }{h}\)
Now multiply by the conjugate.
\(p'(\theta)= \lim_{h \to 0} \dfrac{\sqrt{11}\sqrt{\theta+h} - \sqrt{11}\sqrt{\theta} }{h} \cdot \dfrac{\sqrt{11}\sqrt{\theta+h} + \sqrt{11}\sqrt{\theta} }{\sqrt{11}\sqrt{\theta+h} + \sqrt{11}\sqrt{\theta} } \\\\\\\Longrightarrow p'(\theta)= \lim_{h \to 0} \dfrac{(\sqrt{11}\sqrt{\theta+h} - \sqrt{11}\sqrt{\theta} )(\sqrt{11}\sqrt{\theta+h} + \sqrt{11}\sqrt{\theta} )}{h(\sqrt{11}\sqrt{\theta+h} + \sqrt{11}\sqrt{\theta} )} \\\\\\\)
\(\Longrightarrow p'(\theta)= \lim_{h \to 0} \dfrac{11h}{h(\sqrt{11}\sqrt{\theta+h} + \sqrt{11}\sqrt{\theta} )}\\\\\\\Longrightarrow p'(\theta)= \lim_{h \to 0} \dfrac{11}{\sqrt{11}\sqrt{\theta+h} + \sqrt{11}\sqrt{\theta} }\)
Step 4: Simplify the expression: Evaluate the limit by substituting the value of h=0 into the difference quotient. Simplify the expression as much as possible.
\(p'(\theta)= \lim_{h \to 0} \dfrac{11}{\sqrt{11}\sqrt{\theta+h} + \sqrt{11}\sqrt{\theta} }\\\\\\\Longrightarrow p'(\theta)= \dfrac{11}{\sqrt{11}\sqrt{\theta+(0)} + \sqrt{11}\sqrt{\theta} }\\\\\\\Longrightarrow p'(\theta)= \dfrac{11}{\sqrt{11}\sqrt{\theta} + \sqrt{11}\sqrt{\theta} }\\\\\\\Longrightarrow p'(\theta)= \dfrac{11}{2\sqrt{11}\sqrt{\theta} }\\\\\\\Longrightarrow p'(\theta)= \dfrac{11}{2\sqrt{11\theta} }\\\\\\\Longrightarrow p'(\theta)= \dfrac{11}{2\sqrt{11\theta} }\)
\(\therefore \boxed{\boxed{p'(\theta)= \dfrac{\sqrt{11} }{2\sqrt{\theta} }}}\)
Thus, we have found the derivative on the function using the definition.
It's important to note that in practice, finding derivatives using the definition can be a tedious process, especially for more complex functions. However, the definition lays the foundation for understanding the concept of derivatives and its applications. In practice, there are various rules and techniques, such as the power rule, product rule, and chain rule, that can be applied to find derivatives more efficiently.\(\hrulefill\)
Now evaluating the function at the given points.
\(p'(\theta)= \dfrac{\sqrt{11} }{2\sqrt{\theta}}; \ p'(1)=??, \ p'(11)=??, \ p'(\frac{3}{11} )=??\)
When θ=1:
\(p'(\theta)= \dfrac{\sqrt{11} }{2\sqrt{\theta}}\\\\\\\Longrightarrow p'(1)= \dfrac{\sqrt{11} }{2\sqrt{1}}\\\\\\\therefore \boxed{\boxed{p'(1)= \dfrac{\sqrt{11} }{2}}}\)
When θ=11:
\(p'(\theta)= \dfrac{\sqrt{11} }{2\sqrt{\theta}}\\\\\\\Longrightarrow p'(11)= \dfrac{\sqrt{11} }{2\sqrt{11}}\\\\\\\therefore \boxed{\boxed{p'(11)= \dfrac{1}{2}}}\)
When θ=3/11:
\(p'(\theta)= \dfrac{\sqrt{11} }{2\sqrt{\theta}}\\\\\\\Longrightarrow p'(\frac{3}{11} )= \dfrac{\sqrt{11} }{2\sqrt{\frac{3}{11} }}\\\\\\\therefore \boxed{\boxed{p'(\frac{3}{11} )= \dfrac{11\sqrt{3} }{6}}}\)
Thus, all parts are solved.
WILL GIVE BRIANLEST IM WATCHING
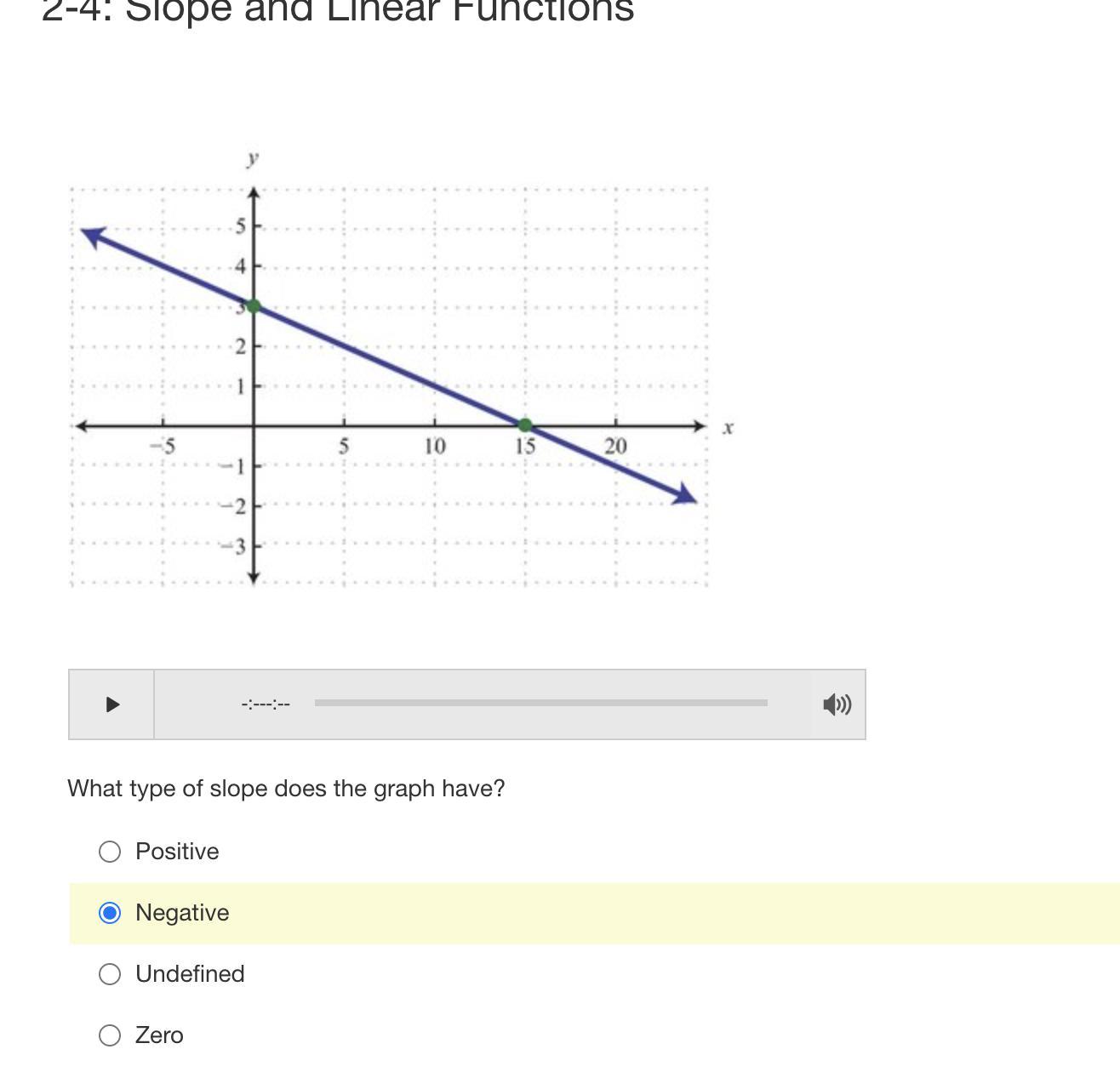
Answers
Answer:
negative
Step-by-step explanation:
♪\(*^▽^*)/\(*^▽^*)/
Which equation shows the point-slope form of the line that passes through (3, 2) and has a slope of y plus StartFraction one-half EndFraction equals 3 left-parenthesis x minus 2 right-parenthesis.?
y + 2 =y plus 2 equals StartFraction one-third EndFraction left-parenthesis x plus 3 right-parenthesis.(x + 3)
y – 2 = y minus 2 equals StartFraction one-third EndFraction left-parenthesis x minus 3 right-parenthesis.(x – 3)
y + 3 = y plus 3 equals StartFraction one-third EndFraction left-parenthesis x plus 2 right-parenthesis.(x + 2)
y – 3 = y plus StartFraction one-half EndFraction equals 2 left-parenthesis x minus 3 right-parenthesis.(x – 2)
Answers
The equation that shows the point-slope form of the line passing through (3, 2) with a slope of (1/2) is:
y - 2 = (1/2)(x - 3)
In the point-slope form of a linear equation, the formula is y - y1 = m(x - x1), where (x1, y1) represents a point on the line, and m represents the slope of the line. By substituting the given values into the formula, we can determine the correct equation.
In this case, the given point is (3, 2) and the slope is (1/2). Plugging these values into the formula, we get:
y - 2 = (1/2)(x - 3)
This equation represents the line passing through the point (3, 2) with a slope of (1/2). It is in the point-slope form, which allows us to easily determine the equation of a line based on a given point and slope.
Therefore, the correct equation is y - 2 = (1/2)(x - 3).
For more such answers on Point slope
https://brainly.com/question/29797287
#SPJ8
Answer: B
Step-by-step explanation:
Consider strings of four decimal digits. Which rule must be used to find the number of strings of four decimal digits that have exactly three digits that are 9s? multiple choice the sum rule the subtraction rule the product rule the division rule How many strings of four decimal digits have exactly three digits that are 9s?
Answers
Answer:
36 possible ways
Step-by-step explanation:
Range of digit : 0 up to 9
To obtain the number of strings of 4 decimal digits that have exactly 3 digits that are 9s ; we use the multiplication rule :
In other to have exactly 3 digits from 4 that are 9s :
Say:
We have 3 9s and the last number could be any of the 10 possible digits except 9
First 9 = 1 possible way (since we have only one 9 between (0 to 9)
Second 9 = 1 possible way
Third 9 = 1 possible way
4th digit = 9 ways (could be any digit between 0 and 9, except 9)
Also, we consider the 4th digit's position ; as it could take up any of different positions in between the 9s = 4 ways
Using the product rule :
1 * 1 * 1 * 9 * 4 = 36 possible ways
Write an equation in standard form of the line that passes through (-4,-4) and has the slope -3/2
Answers
Answer:
y=-1.5x-10
Step-by-step explanation:
standard form is y=mx+b m here is -1.5 -1.5*-4=6 6-10=-4
y=-1.5x-10
What is the value of the expression -3(3+2)
Answers
Answer:
-15
Step-by-step explanation:
write an equation for the line through the point (-7,-4) and parallel to the line y=8x-4 in point-slope form
Answers
The equation for the line through the point (-7,-4) and parallel to the line y = 8x - 4 in point-slope form is y = 8x + 52
How to determine the equation of the second line?The first equation is given as
y = 8x - 4
The slope of the above equation is
m = 8
Parallel lines have equal slope
So, the slope of the other line is
m = 8
The equation is then calculated as
y = m(x - x1) + y1
Where
m = 8
(x1, y1) = (-7, -4)
So, we have
y = 8(x + 7) - 4
Expand
y = 8x + 56 - 4
Evaluate the difference
y = 8x + 52
Hence, the equation for the line through the point (-7,-4) and parallel to the line y = 8x - 4 in point-slope form is y = 8x + 52
Read more about linear equation at:
brainly.com/question/14323743
#SPJ1
evaluate one third of the sum of 15 and 6
Answers
Answer:
7
Step-by-step explanation:
15 plus 6 equals 21
21 divided by 3 is 7
Answer:7
Step-by-step explanation:
sum of 15 and 6
15+6=21
1/3 Of The sum
1/3 of 21
1/3 x 21
(1x21)/3
21/3=7
can someone help me with this

Answers
Answer:
2nd answer option : 6^(13/4)
Step-by-step explanation:
what are we doing, when 2 equal base terms with exponents are multiplied ? we add the exponents !
this is like 3⁴×3³ = 3⁷
because
3×3×3×3 × 3×3×3 = 3×3×3×3×3×3×3 = 3⁷
it is that simple.
and that concept is also valid for any kind of number as exponent. even for fractions and so on.
so,
6^3 × 6^(1/4) = 6^(3 + 1/4) = 6^(12/4 + 1/4) = 6^(13/4)
Solve the compound inequality.
4x-5<-2 or x+1>3
Answers
The solution of the compound inequality is x < 3/4 or x >2.
What is inequality?In mathematics, "inequality" refers to a relationship between two expressions or values that are not equal to each other. To solve the inequality, you may multiply or divide each side by the same positive number, add the same amount to each side, take the same amount away from each side, and more. You must flip the inequality sign if you multiply or divide either side by a negative number.
Given:
A compound inequality:
4x - 5 < -2 or x + 1 > 3.
Solving inequality,
4x < -2 + 5 or x > 2
4x < 3 or x > 2.
x < 3/4 or x >2.
Therefore, the solution is x < 3/4 or x >2.
To learn more about inequality;
brainly.com/question/28823603
#SPJ1
Find the volume of each composite figure to the nearest whole number.

Answers
The volume of the composite figure in this problem is given as follows:
76 ft³.
How to obtain the volume of a rectangular prism?The volume of a rectangular prism, with dimensions defined as length, width and height, is given by the multiplication of these three defined dimensions, according to the equation presented as follows:
Volume = length x width x height.
The figure in this problem is composed by two prisms, with dimensions given as follows:
2 ft, 6 ft and 3 ft.2 ft, 4 ft and 8 - 3 = 5 ft.Hence the volume is given as follows:
2 x 6 x 3 + 2 x 4 x 5 = 76 ft³.
A similar problem about the volume of rectangular prisms is presented at brainly.com/question/22070273
#SPJ1
a histogram showing u.s. household income is highly skewed right. which of following statistics would best describe the center of the distribution? question 10 options: 1) median 2) variance 3) mean 4) mode
Answers
......,,........,.....-.......
The median would best describe the centre of the distribution for a highly skewed right histogram of US household income. The correct option is A.
What is the median?The median is the value that separates the distribution into two equal parts and is less influenced by extreme values than the mean.
Since a highly skewed right distribution has a long tail on the right side, the mean is likely to be pulled towards that tail, making it an unreliable measure of the centre.
The mode, or most frequently occurring value, may not be useful for describing the centre of a skewed distribution. The variance is a measure of the spread or dispersion of the data, not its centre.
To know more about the median follow
https://brainly.com/question/12967310
#SPJ2
Assume that by contributing your education you increase your yearly earning potential from 21,484 to 39,746 if the additional education cost $36,000 in about many years, will a it pay for itself
Answers
Yes, the additional education costing $36,000 will pay for itself in less than 2 years based on the increased earning potential.
To determine whether the additional education costing $36,000 will pay for itself, we need to consider the time it takes to recover the investment through the increased earning potential.
The additional yearly earning potential is the difference between the post-education income ($39,746) and the pre-education income ($21,484), which is $18,262.
To calculate the payback period, we divide the cost of education ($36,000) by the annual increase in earning potential ($18,262).
Payback Period = Cost of Education / Annual Increase in Earning Potential
Payback Period = $36,000 / $18,262
The payback period is approximately 1.97 years, meaning that it would take approximately 1.97 years to recover the cost of education through the increased earning potential.
If the time required to recover the cost is less than the time in which the increased earning potential will be realized, then the additional education would be considered to have paid for itself.
In this case, since the payback period is less than 2 years and the increased earning potential will continue for subsequent years, it can be concluded that the additional education costing $36,000 will pay for itself over time.
For more question on earning visit:
https://brainly.com/question/31903552
#SPJ8
1. Which set of ordered pairs DOES NOT represent a function?
a. (0, 1), (2,3), (3,4), (5,6)
b. (1, 1), (2, 2), (3,3), (4,4)
c. (1,4), (1, 5), (1,6), (1,8)
d. (0,7), (2, 4), (4,7), (5,7)
Answers
Answer:
C.
Step-by-step explanation:
because x value cannot be repeated in an ordered pair
The equation 5y=6 represents purchasing 5 tubs of yogurt for $6 In this
equation, what does the solution represent?
Answers
$6-how much the yogurt costed in total
Please explain how to do it too ill give brainliest

Answers
Answer:
x = 90
Step-by-step explanation:
The given diagram shows a circle with intersecting chords, KM and JL.
To find the value of x, we can use the Angles of Intersecting Chords Theorem.
According to the Angles of Intersecting Chords Theorem, if two chords intersect within a circle, the angle formed at the intersection point is equal to half the sum of the measures of the arcs intercepted by the angle and its corresponding vertical angle.
Let the point of intersection of chords KM and JL be point P.
As the chords are straight lines, angle x° forms a linear pair with angle JPM.
Note: We cannot use the Angles of Intersecting Chords Theorem to find the value of x directly, since we have not been given the measures of the arcs KJ and ML. Therefore, we need to use the theorem to find m∠JPM first.
From inspection of the given diagram:
\(m\overset\frown{JM}=30^{\circ}\)\(m\overset\frown{LK}=(2x - 30)^{\circ}\)Using the Angles of Intersecting Chords Theorem, we can calculate the measure of angle JPM (shown in orange on the attached diagram):
\(\begin{aligned}m \angle JPM &=\dfrac{1}{2}\left(m\overset\frown{JM}+m\overset\frown{LK}\right)\\\\&=\dfrac{1}{2}\left(30^{\circ}+(2x-30)^{\circ}\right)\\\\&=\dfrac{1}{2}\left(30^{\circ}+2x^{\circ}-30^{\circ}\right)\\\\&=\dfrac{1}{2}\left(2x^{\circ}\right)\\\\&=x^{\circ}\end{aligned}\)
As angle JPM forms a linear pair with angle x°, the sum of the two angles equals 180°:
\(\begin{aligned}m \angle JPM+x^{\circ}&=180^{\circ}\\\\x^{\circ}+x^{\circ}&=180^{\circ}\\\\2x^{\circ}&=180^{\circ}\\\\\dfrac{2x^{\circ}}{2}&=\dfrac{180^{\circ}}{2}\\\\x^{\circ}&=90^{\circ}\\\\x&=90\end{aligned}\)
Therefore, the value of x is 90, which means that the two chords intersect at right angles.

Jake has $120 to spend for a party. Juice costs $8. Pizza costs $12. Write the standard equ.
how much juice and pizza Jake can buy?
Answers
Answer:
$8x + $12y = $120
Step-by-step explanation:
x = amount of juice
y = amount of pizza
$120 = his total money
NO LINKS!! URGENT HELP PLEASE!!!
1. Find an exponential function of the form f(x) = ba^-1 + c that has the given horizontal asymptote and y-intercept and passes through P
y = 33; y-intercept 408; P(2, 93)
Answers
Answer:
\(\bold{f(x) = 375(2.5)^{-x}+ 33}\)
Step-by-step explanation:
An exponential function of form f(x) = ba^(-x) + c has a horizontal asymptote of y = c as x approaches infinity, and a y-intercept of (0, b + c). We can use the given information to set up a system of equations and solve for the unknowns.
The horizontal asymptote is given as y = 33, so we have:
c = 33
The y-intercept is given as (0, 408), so we have:
b + c = 408
Substituting c = 33, we get:
b + 33 = 408
b = 375
So the function we're looking for is of the form:
\(\bold{f(x) = 375a^{-x}+ 33}\)
To find a, we use the fact that the function passes through P(2, 93):
93 = 375a^(-2) + 33
60 = 375a^(-2)
a^2 = 375/60
a^2 = 6.25
a = \(\sqrt{6.25 } =2.5\)
Therefore, the exponential function that satisfies the given conditions is:
\(\bold{f(x) = 375(2.5)^{-x}+ 33}\)
What is the value of X? Thanks for the help.
No links please!!

Answers
Answer:
11.5
Step-by-step explanation:
Using pythagoras theorem
whoever answers the question first I'll choose them as brainliest

Answers
derivate (cos(3x^2). (5x^3 -1)^1/3 +sin 4x^3)^4
\( \: \: \: \: find \: first \: derivative \\ ( cos(3x {}^{2} ) \times ( \sqrt[3]{5x {}^{3} - 1} ) + \sin(4x {}^{3} ) {}^{4} \)
Answers
Answer:
Step-by-step explanation:
\(\frac{d}{dx} [cos(3x^2) \sqrt[3]{5x^3 -1} +sin(4x^3)]^4\\\\=4[cos(3x^2) \sqrt[3]{5x^3 -1} +sin(4x^3)]^3\; \frac{d}{dx} [cos(3x^2) \sqrt[3]{5x^3 -1} +sin(4x^3)] --- eq(1)\)
Lets look at the derivative part:
\(\frac{d}{dx} [cos(3x^2) \sqrt[3]{5x^3 -1} +sin(4x^3)] \\\\= \frac{d}{dx}[cos(3x^2) \sqrt[3]{5x^3 -1} ] + \frac{d}{dx}[sin(4x^3)]\\\\=cos(3x^2) \frac{d}{dx}[ \sqrt[3]{5x^3 -1} ] + \sqrt[3]{5x^3 -1}\frac{d}{dx}[ cos(3x^2) ] + cos(4x^3) \frac{d}{dx}[4x^3]\\\\=cos(3x^2) \frac{1}{3} (5x^3 -1)^{\frac{1}{3} -1} \frac{d}{dx}[5x^3 -1] + \sqrt[3]{5x^3 -1} (-sin(3x^2))\frac{d}{dx}[ 3x^2] + cos(4x^3)[(4)(3)x^2]\)
\(=\frac{cos(3x^2) 5(3)x^2}{3(5x^3 - 1)^{\frac{2}{3} }} -\sqrt[3]{5x^3 -1}\; sin(3x^2) (3)(2)x + 12x^2 cos(4x^3)\\\\=\frac{5x^2cos(3x^2) }{(5x^3 - 1)^{\frac{2}{3} }} -6x\sqrt[3]{5x^3 -1}\; sin(3x^2) + 12x^2 cos(4x^3)\)
Substituting in eq(1), we have:
\(\frac{d}{dx} [cos(3x^2) \sqrt[3]{5x^3 -1} +sin(4x^3)]^4\\\\=4[cos(3x^2) \sqrt[3]{5x^3 -1} +sin(4x^3)]^3\; [\frac{5x^2cos(3x^2) }{(5x^3 - 1)^{\frac{2}{3} }} -6x\sqrt[3]{5x^3 -1}\; sin(3x^2) + 12x^2 cos(4x^3)]\)
i need help with this
3:7 = ___: 49
Answers
Answer:
3 : 7 = 21 : 49
Step-by-step explanation:
i need help with this
3:7 = ___: 49
3 : 7 = x : 49
x = 3 × 49 ÷ 7
x = 147 ÷ 7
x = 21
3 : 7 = 21 : 49 (your answer)
7. What is the y-intercept for the equation 5x-2y = -4?
о
(0,-2)
(0,2)
(0, -1/3)
(0,4/5)
Answers
Answer:
(0, 2)
Step-by-step explanation:

Another social worker, who works at a community development organization, makes a different claim. They claim that the average number of children who drop out of high school each day in a particular city is different than 15 children. They would like to carry out a hypothesis test and test the claim that the average number of children who drop out of high school each day in a particular city is different than 15 children. Why is this hypothesis test two-tailed?
Answers
The alternative hypothesis for this hypothesis test is that the average number of children who drop out of high school each day in a particular city is different than 15 children, this is a two-tailed hypothesis test.
This hypothesis test is two-tailed because the alternative hypothesis, which represents the claim made by the social worker, is that the average number of children who drop out of high school each day in a particular city is different than 15 children. This alternative hypothesis is not specifying whether the average is greater or less than 15, but only that it is different. Therefore, the null hypothesis is that the average number of children who drop out of high school each day in a particular city is equal to 15, and the alternative hypothesis is that it is different from 15.
In a two-tailed hypothesis test, the rejection region is split into two parts, one in each tail of the distribution. The significance level is split between the two tails, with half of the significance level in each tail. The critical values are calculated based on the split significance level, and the test statistic is compared to the critical values to determine whether to reject or fail to reject the null hypothesis.
Learn more about average here:
https://brainly.com/question/14402983
#SPJ1
100 POINTS
A gazebo in the shape of a regular octagon has equal sides of 9 feet and an apothem of 10.9 feet.
a. If one side of a gazebo is open, and the other sides have a railing, find the cost of the railing if it sells for $7.90 per foot.
b. Find the area of the gazebo in square feet.
c. Find the cost of the gazebo's flooring if it costs $3 per square foot. Round to the nearest hundred dollars.
Answers
Answer:
a) $497.70
b) 392.4 square feet
c) $1,200
Step-by-step explanation:
Part (a)A regular octagon has 8 sides of equal length.
Given each side of the octagon measures 9 feet in length, and one side does not have a railing, the total length of the railing is 7 times the length of one side:
\(\textsf{Total length of railing}=\sf 7 \times 9\; ft=63\;ft\)
If the railing sells for $7.90 per foot, the total cost of the railing can be calculated by multiplying the total length by the cost per foot:
\(\textsf{Total cost of railing}=\sf 63\;ft \times \dfrac{\$7.90}{ft}=\$497.70\)
Therefore, the cost of the railing is $497.70.
\(\hrulefill\)
Part (b)To find the area of the regular octagonal gazebo, given the side length and apothem, we can use the area of a regular polygon formula:
\(\boxed{\begin{minipage}{6cm}\underline{Area of a regular polygon}\\\\$A=\dfrac{n\;s\;a}{2}$\\\\where:\\\phantom{ww}$\bullet$ $n$ is the number of sides.\\ \phantom{ww}$\bullet$ $s$ is the length of one side.\\ \phantom{ww}$\bullet$ $a$ is the apothem.\\\end{minipage}}\)
Substitute n = 8, s = 9, and a = 10.9 into the formula and solve for A:
\(\begin{aligned}\textsf{Area of the gazebo}&=\sf \dfrac{8 \times 9\:ft \times10.9\:ft}{2}\\\\&=\sf \dfrac{784.8\;ft^2}{2}\\\\&=\sf 392.4\; \sf ft^2\end{aligned}\)
Therefore, the area of the gazebo is 392.4 square feet.
\(\hrulefill\)
Part (c)To calculate the cost of the gazebo's flooring if it costs $3 square foot, multiply the area of the gazebo found in part (b) by the cost per square foot:
\(\begin{aligned}\textsf{Total cost of flooring}&=\sf 392.4\; ft^2 \times \dfrac{\$3}{ft^2}\\&=\sf \$1177.2\\&=\sf \$1200\; (nearest\;hundred\;dollars)\end{aligned}\)
Therefore, the cost of the gazebo's flooring to the nearest hundred dollars is $1,200.
a. To find the perimeter of the gazebo, we can use the formula P = 8s, where s is the length of one side. Substituting s = 9, we get:
P = 8s = 8(9) = 72 feet
Since one side is open, we only need to find the cost of railing for 7 sides. Multiplying the perimeter by 7, we get:
Cost = 7P($7.90/foot) = 7(72 feet)($7.90/foot) = $4,939.20
Therefore, the cost of the railing is $4,939.20.
b. To find the area of the gazebo, we can use the formula A = (1/2)ap, where a is the apothem and p is the perimeter. Substituting a = 10.9 and p = 72, we get:
A = (1/2)(10.9)(72) = 394.56 square feet
Therefore, the area of the gazebo is 394.56 square feet.
c. To find the cost of the flooring, we need to multiply the area by the cost per square foot. Substituting A = 394.56 and the cost per square foot as $3, we get:
Cost = A($3/square foot) = 394.56($3/square foot) = $1,183.68
Rounding to the nearest hundred dollars, the cost of the flooring is $1,184. Therefore, the cost of the gazebo's flooring is $1,184.
#SPJ1
I need help please help me with my math

Answers
A....
B....
C....
D....

Answers
Answer:
B
Step-by-step explanation:
whenever we add 1 to the number of team wins, the attendance number goes up by 15. that is a constant rate.
a constant percentage would change the absolute number of people attending every time.
e.g. let's say there were 100 people attending last time. and the audience increases by 10%. so, next time there are 100 + 10% = 100 + 10 = 110 people attending.
they win again, and the constant percentage of 10% would add now 10% of 110 people = 11 people.
and so on.
the linear function "attendance" would be for x as the number of team wins :
attendance(x) = 15x + c
with c being a starting number of people attending at the first game.