The end behaviour for the polynomial function h(x)=−x3+x4−2x+1 h ( x ) = - x 3 + x 4 - 2 x + 1 is: x→−[infinity], y→−[infinity] x → - [infinity] , y → - [infinity] and x→[infinity], y→[infinity] x → [infinity] , y → [infinity] x→−[infinity], y→[infinity] x → - [infinity] , y → [infinity] and x→[infinity], y→[infinity] x → [infinity] , y → [infinity] x→−[infinity], y→−[infinity] x → - [infinity] , y → - [infinity] and x→[infinity], y→−[infinity] x → [infinity] , y → - [infinity] Unable to tell.
Answers
Answer:
\(\text{As } x \to \infty, y \to \infty,$and as x \to -\infty, y \to \infty\)
Step-by-step explanation:
Given the polynomial function: \(h(x)=-x^3+x^4-2x+1\)
To examine its end behavior, we create a table of values that we can then examine.
\(\left|\begin{array}{c|c}x&h(x)\\--&--\\-4&329\\-3&115\\-2&29\\-1&5\\0&1\\1&-1\\2&5\\3&49\\4&185\end{array}\right|\)
From the table, we see a repeating pattern of positive values of h(x) with h(1)=-1 being an axis of symmetry.
Therefore, as:
\(x \to \infty, h(x) \to \infty\\x \to -\infty, h(x) \to \infty\)
Related Questions
(vi) any current larger than 15 ma will permanently damage the led.
the resistor in the circuit has a resistance of 270 n.
use the results from the investigation to determine the maximum voltage of
the power supply without damaging the led.
(4)
Answers
To determine the maximum voltage of the power supply without damaging the LED, we need more information about the LED's specifications. The resistance of the resistor alone cannot provide enough information to calculate the maximum voltage.
How the current damage led permanently?LEDs have a maximum forward voltage rating, beyond which excessive voltage can damage them. This rating varies depending on the type and color of the LED. Additionally, LEDs typically require a current-limiting resistor to prevent excessive current flow.
To calculate the appropriate current-limiting resistor value and maximum voltage for the LED, we need the following information:
Forward voltage (Vf) rating of the LED: This is the voltage required for the LED to operate correctly. It can typically be found in the LED's datasheet or product specifications.
Forward current (If) rating of the LED: This is the recommended operating current for the LED, usually specified in milliamperes (mA) or amperes (A).
With these values, we can determine the maximum voltage of the power supply using Ohm's law and the LED's characteristics:
Calculate the current (I) flowing through the LED:
I = If (recommended forward current)
Calculate the resistance value (R) for the current-limiting resistor:
R = (Vp - Vf) / I
Where Vp is the power supply voltage and Vf is the forward voltage of the LED.
Use the resistance value (R) obtained to find the maximum voltage:
Vp(max) = Vf + I x R
Please provide the forward voltage and forward current ratings of the LED for a more accurate calculation.
Learn more about: power supply
brainly.com/question/32151541
#SPY11
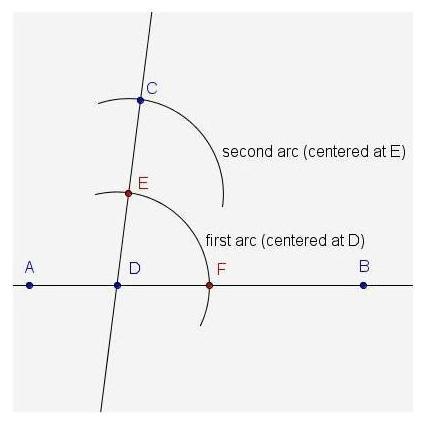
What needs to be corrected in this construction of a line parallel to line AB passing through C?
A and B endpoints of line segment is intersected at point D with a transversal. D as center, arc 1 is drawn above intersecting transversal at point E, and at point F on the segment. E as center, arc 2 is drawn intersecting the transversal at point C.
A.
The first arc should pass through C.
B.
The first arc should be centered at C.
C.
The second arc should be centered at C.
D.
The second arc should cross the first arc.
E.
The second arc should be centered at F.
Answers
The option that needs to be corrected in this construction of a line parallel to line AB passing through C is C: the second arc should be centered at C.
Why should the second arc be centered at C?The second arc should be centered at C because as it crosses passing through Line C, it is seen that it was not touching or intersecting AB and so one can say that it is parallel to it.
Looking at the other lines, we will see that they are all touching AB and are not running parallel to it.
Hence, The option that needs to be corrected in this construction of a line parallel to line AB passing through C is C: the second arc should be centered at C.
Learn more about line parallel;
brainly.com/question/1439525
#SPJ1
Anna does sit-ups to get ready for her first triathlon. When she starts, she does a sit-up every 2 seconds. But, as she gets tired, each sit-up takes longer and longer to do.
Answers
Answer:
the answer is no
Step-by-step explanation:
khan acadmy
Answer:
no
Step-by-step explanation:
did it on khan
Hi, I cannot figure out this question, can anyone help?

Answers
Answer:
(8+-4)(6+-2)(5+-1)
Step-by-step explanation:
i.) 8+(-4)
8-4=4
ii) 6+(-2)
6-2=4
iii) 5+(-1)
5-1 = 4
HOPE THIS HELPS
Answer:
(8+-4)(6+-2)(5+-1)
Step-by-step explanation:
Find all the missing elements:
15
38°
42°
A
C С
b

Answers
Answer:
m∠B = 100°
a = 4.6
b = 7.36
Step-by-step explanation:
By applying sine rule in the given triangle,
\(\frac{\text{sin(A)}}{a}= \frac{\text{sin(B)}}{b}= \frac{\text{sin(C)}}{c}\)
Now substitute the values in the expression,
\(\frac{\text{sin(38)}}{a}= \frac{\text{sin(B)}}{b}= \frac{\text{sin(42)}}{5}\)
\(\frac{\text{sin(38)}}{a}= \frac{\text{sin(42)}}{5}\)
\(a=\frac{5\text{sin(38)}}{\text{sin(42)}}\)
a = 4.6
By applying triangle sum theorem in ΔABC,
m∠A + m∠B + m∠C = 180°
38° + m∠B + 42° = 180°
m∠B = 180° - 80°
m∠B = 100°
\(\frac{\text{sin(100)}}{b}= \frac{\text{sin(42)}}{5}\)
\(b=\frac{5\text{sin(100)}}{\text{sin(42)}}\)
b = 7.36
Deepa needed to get her computer fixed. She took it to the repair store. The technician at the store worked on the computer for 4. 25 hours and charged her $167 for parts. The total was $655. 75. Write and solve an equation which can be used to determine xx, the cost of the labor per hour.
Answers
The cost of the labor per hour is 115 hours.
The equation is going to be:
4.25x + 167 = 655.75
your x is going to be:115
The duration was 4.25 hours.
The parts cost 167.
Cost in full: 655.75
so the price per hour is x.
As a result, when you write your equation, the total number of hours (multiplied by the cost per hour) will be added to the cost of the parts, and the sum of these two amounts will be your total cost.
In order to solve the problem, you must deduct the cost of each component from the total cost. This should give you the following result: 4.25x = 488.75
After that, divide 4.25 by each side as you normally would.
The cost of labor per hour follows. 115
Know more about Equations at:
https://brainly.com/question/26310043
#SPJ4
Write in slope-intercept form (solve for y): 5x - 2y = 8
Answers
Answer:
y = 5/2 x - 4
Step-by-step explanation:
For slope-intercept form, just solve for y:
5x - 2y = 8
\(\frac{5x}{2} - \frac{8}{2} = \frac{2y}{2}\)
5/2 x - 4 = y or
y = 5/2 x - 4
The slope intercept form is y= 5/2x - 4.
What is Slope?A line's slope is determined by how its y coordinate changes in relation to how its x coordinate changes. y and x are the net changes in the y and x coordinates, respectively. Therefore, it is possible to write the
change in y coordinate with respect to the change in x coordinate as,
m = Δy/Δx where, m is the slope
We have the Equation
5x - 2y = 8.
As, we know from the slope intercept form
y= mx + b
So, 5x - 2y = 8
5x - 8 = 2y
5/2x - 8/2 = y
y= 5/2x - 4
where slope is 5/2 and y intercept is -4.
Learn more about Slope here:
https://brainly.com/question/3605446
#SPJ2
use the drag-and-drop tiles to determine whether the number is rational or not rational
Answers
Answer:
The correct answer is not rational.
Step-by-step explanation:
Can someone explain to me what 8√42 ÷ 2√7 is?
Answers
Answer:
Step-by-step explanation:
8√42 ÷ 2√7 is 8√42/2√7 in a fraction form
you want to take the square root out of the denominator, and so you would multiply the denominator by the numerator and itself.
8√42/2√7 * 2√7/2√7 = 4√6
Complete the work to find the length of HD.

Answers
Answer:
\(HD=5.5\)
Step-by-step explanation:
\(4(HD)=22 \implies HD=5.5\)
For each generated solid, find the volume, and sketch the solid. 1. The region between the line y = 1 and the graph of y=√x+1, 05.x≤ 4 is revolved about the x-axis. 2. The region between the lines x = 4, y=x-2 and the x-axis in the first quadrant is revolved about the y-axis. 3. The region between the x-axis and the line y=-x+6 in the first quadrant is revolved about the y-axis 4. The region between the x-axis and the graph of y=sinx, 0≤x≤ is revolved about the line x=2.
Answers
The region between the line y = 1 and the graph of y = √(x + 1), 0 ≤ x ≤ 4 is revolved about the x-axis.We need to integrate this using the washer method. We start by finding the volume of the individual washers:V = π(R^2 - r^2)hWe need to find R, r, and h for this.
We can express the volume of the solid as follows:
V = ∫(πy^2)dx
Let's put it to the test now:
π∫[0,4][1 - (√(x + 1))^2]dx= π∫[0,4](1 - x + 1)dx= π∫[0,4](2 - x)dx= π[x(2 - x) - (1/2)(x^2)]|[0,4]= π(4 - (1/2)(16) - 0 + (1/2)(0))= (3π)/2
The volume of the region between the line y = 1 and the graph of y = √(x + 1), 0 ≤ x ≤ 4 is revolved about the x-axis is (3π)/2.2. The region between the lines x = 4, y = x - 2, and the x-axis in the first quadrant is revolved about the y-axis.We can express the volume of the solid as follows:
V = ∫(2πx)(x - 4)dx
Let's put it to the test now:
2π∫[0,2](x^2 - 4x)dx= 2π[((1/3)(2^3) - 4(1/2)(2^2)) - 0]= (4π)/3
The volume of the region between the lines x = 4, y = x - 2, and the x-axis in the first quadrant is revolved about the y-axis is (4π)/3.
The region between the x-axis and the line y = -x + 6 in the first quadrant is revolved about the y-axis.The volume of the solid is calculated as follows:
V = ∫(2πx)(-x + 6)dx
Let's put it to the test now:
2π∫[0,6](x^2 - 6x)dx= 2π[((1/3)(6^3) - 6(1/2)(6^2)) - 0]= (36π)/3= 12π
The volume of the region between the x-axis and the line y = -x + 6 in the first quadrant is revolved about the y-axis is 12π.4. The region between the x-axis and the graph of y = sin x, 0 ≤ x ≤ π is revolved about the line x = 2.Using the washer method, we can evaluate the volume of the solid. The equation we'll use is:
V = ∫(πR^2 - πr^2)dx
Let's put it to the test now:
π∫[0,π]((2 + sin x)^2 - 4)dx= π∫[0,π](4 + 4sin x + sin^2x - 4)dx= π∫[0,π](4sin x + sin^2x)dx= π(-4cos x - (1/3)cos^3x)|[0,π]= (16π/3)
The volume of the region between the x-axis and the graph of y = sin x, 0 ≤ x ≤ π is revolved about the line x = 2 is (16π/3).
To learn more about washer method visit:
brainly.com/question/30637777
#SPJ11
a 65 foot ladder is leaning against a well. Its lower end is 25 feet away from the wall. How much farther away will it be if upper end is moved down 8 feet?
Answers
=====================================================
Explanation:
Check out the diagrams below.
We'll start with the left diagram (marked "before") which is a right triangle with the horizontal leg of 25 feet and hypotenuse 65 feet.
Use the pythagorean theorem to find the vertical side x.
a^2 + b^2 = c^2
25^2 + x^2 = 65^2
625 + x^2 = 4225
x^2 = 4225 - 625
x^2 = 3600
x = sqrt(3600)
x = 60
The top of the ladder is 60 feet high when placed against the wall in this configuration.
------------------
If the upper end is moved down 8 feet, then x-8 = 60-8 = 52 feet is the new height of the ladder. Refer to the "after" in the diagram below.
Like earlier, we'll use the pythagorean theorem to find the missing side.
a^2 + b^2 = c^2
y^2 + 52^2 = 65^2
y^2 + 2704 = 4225
y^2 = 4225 - 2704
y^2 = 1521
y = sqrt(1521)
y = 39
The horizontal distance from the ladder base to the wall is now 39 feet.
Earlier it was 25 feet, so it has increased by 39-25 = 14 feet.

It takes Jada 20 minutes to walk to school. It takes Andre 80% as long to walk to school. How many minutes does it take Andre to walk to school?
Answers
Answer: 19.2 is how long
Step-by-step explanation:
Answer:
16 minutes
Step-by-step explanation:
Basically I just found out what 10 percent of 20 was, which is 2, then multiplied 2 by 8, to get 16 minutes.
hi I don't understand what to do here pls help
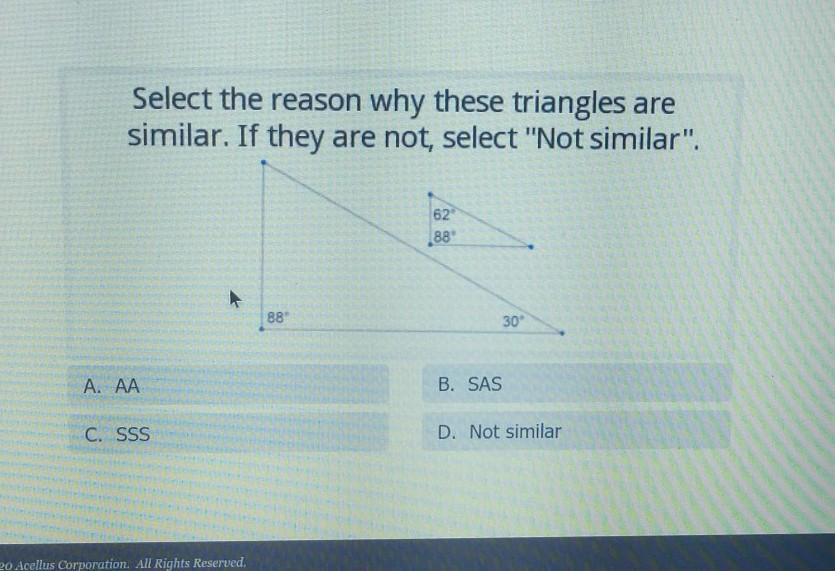
Answers
Answer:
heres what i think..
Step-by-step explanation:
the triangles can be similar as long as they have the same angle,but different measurements, a similar triangle could be a translation,dilation, or enlargement, as long as they are at the same angle (not rotated, reflected, or transformed ect.).
.The FBI wants to determine the effectiveness of their 10 Most Wanted list. To do so, they need to find out the fraction of people who appear on the list that are actually caught.
Step 1 of 2:
Suppose a sample of 434 suspected criminals is drawn. Of these people, 169 were captured. Using the data, estimate the proportion of people who were caught after being on the 10 Most Wanted list. Enter your answer as a fraction or a decimal number rounded to three decimal places.
Step 2 of 2:
Suppose a sample of 434 suspected criminals is drawn. Of these people, 169 were captured. Using the data, construct the 80% confidence interval for the population proportion of people who are captured after appearing on the 10 Most Wanted list. Round your answers to three decimal places.
Answers
Answer:
Step 1:
The proportion of people who were caught after being on the 10 Most Wanted list can be estimated as:
(number of people caught) / (total number of suspected criminals)
Substituting the given values, we get:
169 / 434 ≈ 0.389 (rounded to three decimal places)
So the estimated proportion of people caught after being on the 10 Most Wanted list is 0.389.
Step 2:
To construct an 80% confidence interval for the population proportion of people caught, we can use the following formula:
p ± z* sqrt(p*(1-p)/n)
where p is the sample proportion, z* is the z-score corresponding to the desired confidence level (80% in this case), and n is the sample size.
Substituting the given values, we get:
0.389 ± 1.282 * sqrt(0.389*(1-0.389)/434)
Simplifying this expression, we get:
0.389 ± 0.049
Therefore, the 80% confidence interval for the population proportion of people caught is:
(0.340, 0.438)
Rounded to three decimal places, this becomes:
(0.340, 0.438)
Step-by-step explanation:
What is the best way to study ( in particular for an Algebra test ) ?
Answers
By reviewing your class notes.
Sure hope this helps!
Answer:
Step-by-step explanation:
Learn the material with examples, and do lots of problems. The more problems you solve, the more familiar you become with the problems and the faster and better you will answer the questions.
Find the domain and range of the following rational function. Use any notation. f(x)=(3)/(x-1) f(x)=(2x)/(x-4) f(x)=(x+3)/(5x-5) f(x)=(2+x)/(2x) f(x)=((x^(2)+4x+3))/(x^(2)-9)
Answers
Domain and Range of the given rational functions are:Given rational function f(x) = 3/(x-1)The denominator of f(x) cannot be zero.x ≠ 1 Therefore the domain of f(x) is {x | x ≠ 1}
The range of f(x) is all real numbers except zero.Given rational function f(x) = (2x)/(x-4)The denominator of f(x) cannot be zero.x ≠ 4 Therefore the domain of f(x) is {x | x ≠ 4}The range of f(x) is all real numbers except zero.Given rational function f(x) = (x+3)/(5x-5)The denominator of f(x) cannot be zero.5x - 5 ≠ 0x ≠ 1 Therefore the domain of f(x) is {x | x ≠ 1}The range of f(x) is all real numbers except 1/5.Given rational function f(x) = (2+x)/(2x)The denominator of f(x) cannot be zero.x ≠ 0 Therefore the domain of f(x) is {x | x ≠ 0}The range of f(x) is all real numbers except zero.Given rational function f(x) = (x^2+4x+3)/(x^2-9)For the denominator of f(x) to exist,x ≠ 3, -3
Therefore the domain of f(x) is {x | x ≠ 3, x ≠ -3}The range of f(x) is all real numbers except 1, -1. Function Domain Rangef(x) = 3/(x-1) {x | x ≠ 1} All real numbers except zerof(x) = (2x)/(x-4) {x | x ≠ 4} All real numbers except zerof(x) = (x+3)/(5x-5) {x | x ≠ 1} All real numbers except 1/5f(x) = (2+x)/(2x) {x | x ≠ 0} All real numbers except zerof(x) = (x^2+4x+3)/(x^2-9) {x | x ≠ 3, x ≠ -3} All real numbers except 1, -1
To know more about rational functions visit:
https://brainly.com/question/27914791
#SPJ11
28 In the diagram below of circle O, secant ABC and tangent AD are drawn.
If CA=12.5 and CB=4.5 determine and state the length of DA
Answers
The length of the side DA from secant theorem is; 10
How to find the length of a Tangent?
From the cyclic diagram attached;
Since CA = 12.5 and CB = 4.5, it means that;
BA = 12.5 - 4.5 = 8
From the secant theorem, we know that;
The product of the secant and its exterior segment is equal to the square of the tangent segment.
Thus;
Length of DA = √(8 * 12.5)
Length of DA = 10
Read more about Length of Tangent at; https://brainly.com/question/9132922
#SPJ1

The measure of angle CDE is
degrees.

Answers
CDE = CDB + BDA + ADE
CDE = 42° + 37° + 20°
CDE = 99°
hope it helps...!!!
Answer:99 degrees
Step-by-step explanation:
Angle CDB + Angle BDA + Angle ADE= Angle CDE
42+37+20=99
A scientist uses a submarine to study ocean life.
• She begins at sea level, which is an elevation of o
feet.
. She travels down 20.6 feet.
. She then rises 12.5 feet.
• Next, she descends a second time, 32.4 feet.
How many feet must she now ascend to get back to
sea level?
Answers
Based on the illustration given above, the feet that she now need to ascend to get back to sea level is 40.5.
What is the sea level about?Note that the first descend was 20.6 - 12.5 =
8.1 feet
Then she drop 32.4 feet again
So to get back up she need to add:
= 32.4 feet + 8.1 feet
= 40.5
Therefore, based on the calculation given above, the feet that she now need to ascend to get back to sea level is 40.5.
Learn more about sea level from
https://brainly.com/question/2092614
#SPJ1
let a and b be integers. prove that if ab = 4, then (a – b)3 – 9(a – b) = 0.
Answers
Let \(\(a\)\) and \(\(b\)\) be integers such that \(\(ab = 4\)\). We want to prove that \(\((a - b)^3 - 9(a - b) = 0\).\)
Starting with the left side of the equation, we have:
\(\((a - b)^3 - 9(a - b)\)\)
Using the identity \(\((x - y)^3 = x^3 - 3x^2y + 3xy^2 - y^3\)\), we can expand the cube of the binomial \((a - b)\):
\(\(a^3 - 3a^2b + 3ab^2 - b^3 - 9(a - b)\)\)
Rearranging the terms, we have:
\(\(a^3 - b^3 - 3a^2b + 3ab^2 - 9a + 9b\)\)
Since \(\(ab = 4\)\), we can substitute \(\(4\)\) for \(\(ab\)\) in the equation:
\(\(a^3 - b^3 - 3a^2(4) + 3a(4^2) - 9a + 9b\)\)
Simplifying further, we get:
\(\(a^3 - b^3 - 12a^2 + 48a - 9a + 9b\)\)
Now, notice that \(\(a^3 - b^3\)\) can be factored as \(\((a - b)(a^2 + ab + b^2)\):\)
\(\((a - b)(a^2 + ab + b^2) - 12a^2 + 48a - 9a + 9b\)\)
Since \(\(ab = 4\)\), we can substitute \(\(4\)\) for \(\(ab\)\) in the equation:
\(\((a - b)(a^2 + 4 + b^2) - 12a^2 + 48a - 9a + 9b\)\)
Simplifying further, we get:
\(\((a - b)(a^2 + 4 + b^2) - 12a^2 + 39a + 9b\)\)
Now, we can observe that \(\(a^2 + 4 + b^2\)\) is always greater than or equal to \(\(0\)\) since it involves the sum of squares, which is non-negative.
Therefore, \(\((a - b)(a^2 + 4 + b^2) - 12a^2 + 39a + 9b\)\) will be equal to \(\(0\)\) if and only if \(\(a - b = 0\)\) since the expression \(\((a - b)(a^2 + 4 + b^2)\)\) will be equal to \(\(0\)\) only when \(\(a - b = 0\).\)
Hence, we have proved that if \(\(ab = 4\)\), then \(\((a - b)^3 - 9(a - b) = 0\).\)
To know more about satisfies visit-
brainly.com/question/16993710
#SPJ11
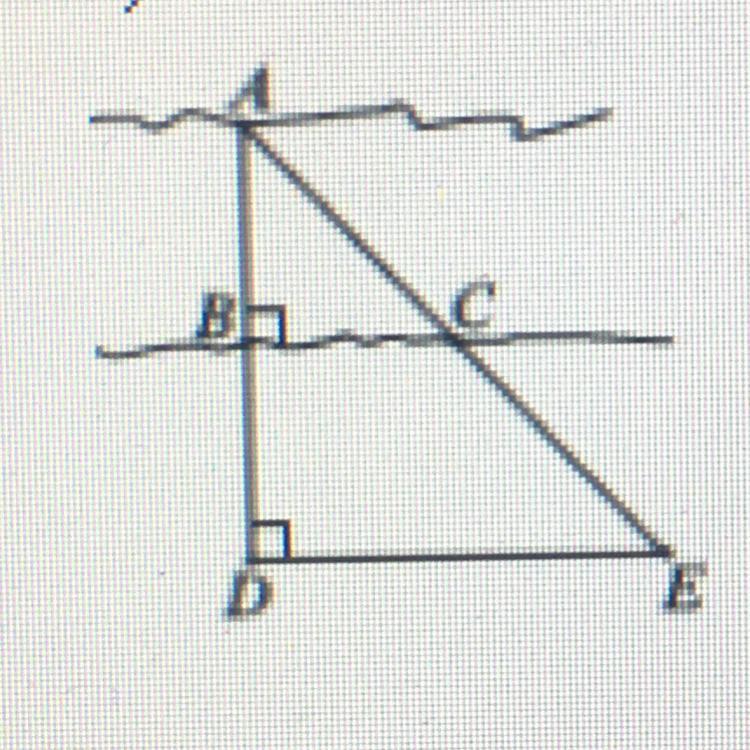
BD = 21 m,
RC = 25 m.
DE = 40 m.
AB = ? m.
Find AB
Answers
Given:
Consider the given sides are,
\(BD=21m\)
\(BC=25m\)
\(DE=40m\)
\(AB=xm\)
To find:
The measure of AB.
Solution:
Let x be the measure of AB.
From the given figure it is clear that,
\(\angle ADE \cong \angle ABC\) (Right angles)
\(\angle ADE \cong \angle ABC\) (Corresponding angles)
Two corresponding angles are congruent. So, by AA property of similarity,
\(\Delta ABC\sim \Delta ADE\)
Corresponding sides of similar triangle are proportional.
\(\dfrac{AB}{BC}=\dfrac{AD}{DE}\)
\(\dfrac{x}{25}=\dfrac{(x+21)}{40}\)
\(40x=25(x+21)\)
\(40x=25x+525\)
Isolating x, we get
\(40x-25x=525\)
\(15x=525\)
\(x=\dfrac{525}{15}\)
\(x=35\)
Therefore, the measure of AB is 35 m.
A plane traveled 3355 miles with the wind in 5.5 hours and 2585 miles against the wind in the same amount of time. Find the speed of the plane in still air and the speed of the wind.
HELP QUICKKKKK
Answers
Answer:
Speed of the plane in still air is 540 mph,Speed of the wind is 70 mph
=======================
Let the speed of plane is x and speed of the wind is y.
The speed of the plane with the wind is x + y and speed of the plane against the wind is x - y.
Equation for speed:
speed = distance / timeSince the same amount of time spent in both cases, we can set equations:
x + y = 3355/5.5 ⇒ x + y = 610x - y = 2585/5.5 ⇒ x - y = 470Add up the two equations and solve for x:
x + y + x - y = 610 + 4702x = 1080x = 540Find y:
540 + y = 610y = 610 - 540y = 70how many solutions does y=x+4 and y=2x+4 have?
Answers
Answer:
x = 0
Step-by-step explanation:
y = x + 4 and y = 2x + 4
Let's solve
x + 4 = 2x + 4
-x + 4 = 4
-x = 0
x = 0
So, there is only one solution is x = 0
The two lines have the same y-intercept, and therefore, that’s one solution there. But because the line will never cross other than at y=4, the two equations will only have 1 solution.
Hope this helped!
Solve the equation 1/2(2x+2)-1/4(3x-1)=15
Answers
Answer:
it is algebraic expression
Alex, Sara and Henry share £112 in a ratio 3:3:2. How much money does each person get?
Answers
Answer:
Step-by-step explanation:
3:3:2 = 3x +2x +3x = 8x
112 = 8x
x = 14
alex = 3x = 3(14) = 42
sara = alex = 42
henry = 2x = 28
(4 points) Find the auxiliary equation for the following DE: y"" - 4y" + 3y' - 12y = 0.
Answers
a. To solve the given initial value problem (IVP) using Laplace transforms, we can apply the Laplace transform to the differential equation and solve for the Laplace transform of the solution.
Taking the Laplace transform of the equation y'(t) + y(t) = (1-3), we have:
sY(s) - y(0) + Y(s) = (1-3)/s
Substituting the initial condition y(0) = 2, we have:
sY(s) - 2 + Y(s) = (1-3)/s
Now, rearranging the equation to solve for Y(s), we get:
Y(s) = (1-3)/s + 2/(s+1)
Simplifying further, we have:
Y(s) = (-2)/s + 2/(s+1)
b. To obtain the solution y(t), we can apply the inverse Laplace transform to Y(s) obtained in part (a).
Taking the inverse Laplace transform, we have:
y(t) = -2 + 2e^(-t)
Therefore, the solution to the given initial value problem is y(t) = -2 + 2e^(-t).
Explanation:
In the first part, we applied the Laplace transform to the differential equation and obtained the equation in terms of the Laplace transform Y(s). By rearranging the equation, we solved for Y(s) in terms of the given Laplace transform expression.
In the second part, we applied the inverse Laplace transform to Y(s) to obtain the solution y(t). The inverse Laplace transform of -2/s gives us a constant term of -2, while the inverse Laplace transform of 2/(s+1) gives us the exponential term 2e^(-t).
Therefore, the solution y(t) = -2 + 2e^(-t) satisfies the differential equation y'(t) + y(t) = (1-3) and the initial condition y(0) = 2.
a. To find the auxiliary equation for the given differential equation y'' - 4y' + 3y' - 12y = 0, we can substitute y = e^(rt) into the equation, where r is an unknown constant.
Substituting y = e^(rt) into the differential equation, we get:
r²e^(rt) - 4re^(rt) + 3e^(rt) - 12e^(rt) = 0
Factoring out e^(rt), we have:
e^(rt)(r² - 4r + 3 - 12) = 0
Simplifying further, we obtain:
e^(rt)(r² - 4r - 9) = 0
Therefore, the auxiliary equation for the given differential equation is r² - 4r - 9 = 0.
b. The auxiliary equation plays a crucial role in finding the solutions to the given differential equation. By solving the auxiliary equation, we can determine the types of solutions and their behavior.
The auxiliary equation for the given differential equation y'' - 4y' + 3y' - 12y = 0 is r² - 4r - 9 = 0. This is a quadratic equation in terms of the unknown constant r.
To solve the quadratic equation, we can use various methods such as factoring, completing the square, or using the quadratic formula. In this case, the quadratic equation does not factor easily, so we can use the quadratic formula:
r = (-(-4) ± √((-4)² - 4(1)(-9))) / (2(1))
Simplifying further, we have:
r = (4 ± √(16 + 36)) / 2
r = (4 ± √52) / 2
r = (4 ± 2√13) / 2
r = 2 ± √13
Therefore, the solutions to the auxiliary equation are r₁ = 2 + √13 and r₂ = 2 - √13.
To learn more about auxiliary equation
brainly.com/question/31605695
#SPJ11
acellus algebra 2. piece wised functions.
find f(-2) for the piece wised function

Answers
\(f(-2) = -4\) for the given piecewise function by using the equation \(f(x) = x - 2\) if \(x < 3.\)
What is the piecewise function?A piecewise function is a mathematical function that is defined differently on different parts of its domain.
Instead of having a single formula that applies to the entire domain, a piecewise function has multiple formulas, each applying to a specific interval or subset of the domain.
To find f(-2) for the given piecewise function, we need to determine which piece applies to the input value o \(f -2\), which is less than 3. Therefore, we use the first piece of the function, which is\(f(x) = x - 2 if x < 3.\)
Substituting x = -2 into this piece, we get:
\(f(-2) = (-2) - 2 = -4\)
Therefore, f(-2) = -4 for the given piecewise function.
Learn more about the equations here :
brainly.com/question/12788590
#SPJ1
certain kind of sheet metal has, on average, 7 defects per 20 square feet. assuming a poisson distribution, find the probability that a 34 square foot metal sheet has at least 9 defects. round your answer to four decimals.
Answers
The probability that a 34 square foot metal sheet has at least 9 defects is 0.4308, rounded to four decimals.
Given that the sheet metal has an average of 7 defects per 20 square feet, we can find the rate parameter (λ) of the Poisson distribution as follows:
λ = (7 defects / 20 sq ft) = 0.35 defects per square foot
Let X be the number of defects in a 34 square foot metal sheet. Since X follows a Poisson distribution with rate parameter λ, we can find the probability that X is at least 9 defects using the cumulative distribution function (CDF) of the Poisson distribution:
P(X ≥ 9) = 1 - P(X < 9) = 1 - F(8)
where F(k) is the CDF of the Poisson distribution with rate parameter λ evaluated at k.
Using the Poisson distribution formula for F(k), we have:
F(k) = P(X ≤ k) = ∑(i=0 to k) [(λ^i * e^(-λ)) / i!]
Using a calculator or software, we can find that:
F(8) = P(X ≤ 8) = 0.5692
Therefore, we have:
P(X ≥ 9) = 1 - F(8) = 1 - 0.5692 = 0.4308
To learn more about probability here:
https://brainly.com/question/30034780
#SPJ4
You are the owner of the biggest and newest roller coaster called the Gentle Giant. The roller coaster costs $6 to ride. The operator of the ride must pay $200 per day for the ride rental and $65 per day for a safety inspection. If you want to make a profit of at least $1,000 each day, what is the minimum number of people that must ride the roller coaster? Write an inequality that can be used to find the minimum number of people, , which must ride the roller coaster each day to make the daily profit.
Answers
Answer:
Inequality: 6r - 200 - 65 \(\geq\) 1000 and minimum of 211 people
Step-by-step explanation:
Let r = rides
6r - 200 - 65 \(\geq\) 1000
6r - 265 \(\geq\) 1000
6r \(\geq\) 1265
r \(\geq\) 210 \(\frac{5}{6}\)
Needs 211 people to make a profit of at least $1000