The finding that average IQ has increased steadily over the 20th century is referred to as the ______________.
Answers
The finding that average IQ has increased steadily over the 20th century is referred to as the Flynn effect.
The Flynn effect is the observation that the average IQ has risen continuously over the 20th century.The Flynn effect is what?The Flynn effect is the finding that IQ levels in the general population rise over time and across generations.
For instance, during the past century, IQ scores have continuously risen in industrialised nations by about 3 points every decade. James R. Flynn, a political scientist from New Zealand who first observed this pattern, created the phrase "Flynn effect" in 1987.
The Flynn effect is significant because it demonstrates that IQ levels are not constant but can alter due to environmental factors. It also emphasises how challenging it is to define and assess intelligence, particularly when contrasting populations from various historical periods or cultural backgrounds.
To know more about Flynn effect refer here:
https://brainly.com/question/11772792#
#SPJ11
Related Questions
A student has money in three accounts that pay 5%, 7%, and 8%, in annual simple (i.e. compounded once per year) interest. She has three times as much invested at 8% as she does at 5%. If the total amount she has invested is $1600 and her interest for the year comes to $115, how much money does she have in each account
Answers
Answer:
Amount invested in account with 5% annual interest = $300
Amount invested in account with 7% annual interest = $400
Amount invested in account with 8% annual interest = $900
Step-by-step explanation:
Let the money invested in account with 5% annual interest = \(x\)
As per question statement,
Money invested in account with 8% annual interest = \(3x\)
Given that total amount invested in three accounts = $1600
So, Money invested in account with 7% annual interest = 1600- \(3x\) -\(x\) = 1600- \(4x\)
For one year, the compound interest is same as that of Simple Interest.
Formula for simple interest is given as:
\(SI =\dfrac{PRT}{100}\)
Where, P is the amount invested
R is the annual rate of interest
T is the time for which the amount is invested.
As per question statement:
\(\dfrac{x\times 5\times 1}{100}+\dfrac{(1600-4x)\times 7\times 1}{100}+\dfrac{3x\times 8\times 1}{100} =115\\\Rightarrow 5x\times +1600\times 7-28x+24x=11500\\\Rightarrow 29x-28x = 11500-11200\\\Rightarrow \bold{x =\$300}\)
Amount invested in account with 5% annual interest = $300
Amount invested in account with 7% annual interest = $1600-$1200 = $400
Amount invested in account with 8% annual interest = $900
calculate the coefficient of variation for a sample of cereal boxes with a mean weight of 340 grams and a standard deviation of 5.2 grams.? 0.15% A
1.53% B
15.29% C
0.65% D
Answers
The coefficient of variation (CV) is a measure of relative variability and is calculated by dividing the standard deviation by the mean, and then multiplying by 100 to express it as a percentage.
In this case, the mean weight is 340 grams, and the standard deviation is 5.2 grams.
CV = (Standard Deviation / Mean) * 100
CV = (5.2 / 340) * 100
CV ≈ 1.53%
Therefore, the correct answer is option B: 1.53%.
To know more about Mean visit-
brainly.com/question/26062194
#SPJ11
AC is a diameter of OE, the area of
the
circle is 2897 units², and AB = 16 units.
Find BC and mBC.
B
A
C
E

Answers
Given that AC is a diameter of the circle, we can conclude that triangle ABC is a right triangle, with AC being the hypotenuse. The area of the circle is not directly related to finding the lengths of BC or AB, so we will focus on the given information: AB = 16 units.
Using the Pythagorean theorem, we can find BC. The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse (AC) is equal to the sum of the squares of the other two sides (AB and BC):
AC² = AB² + BC²
Substituting the given values, we have:
(AC)² = (AB)² + (BC)²
(AC)² = 16² + (BC)²
(AC)² = 256 + (BC)²
Now, we need to find the length of AC. Since AC is a diameter of the circle, the length of AC is equal to twice the radius of the circle.
AC = 2 * radius
To find the radius, we can use the formula for the area of a circle:
Area = π * radius²
Given that the area of the circle is 2897 units², we can solve for the radius:
2897 = π * radius²
radius² = 2897 / π
radius = √(2897 / π)
Now we have the length of AC, which is equal to twice the radius. We can substitute this value into the equation:
(2 * radius)² = 256 + (BC)²
4 * radius² = 256 + (BC)²
Substituting the value of radius, we have:
4 * (√(2897 / π))² = 256 + (BC)²
4 * (2897 / π) = 256 + (BC)²
Simplifying the equation gives:
(4 * 2897) / π = 256 + (BC)²
BC² = (4 * 2897) / π - 256
Now we can solve for BC by taking the square root of both sides:
BC = √((4 * 2897) / π - 256)
To find the measure of angle BC (mBC), we know that triangle ABC is a right triangle, so angle B will be 90 degrees.
In summary:
BC = √((4 * 2897) / π - 256)
mBC = 90 degrees
for similar questions on area of the circle.
https://brainly.com/question/14068861
#SPJ8
Do ALL These Questions CORRECT And You Get Brainliest And 35 Points! Also ill Follow You!

Answers
The image doesn't load for me.
Please help asap, correct answer will get brainliest

Answers
Answer:
im not sure if my answer is correct
Select the correct answer. If function f has zeros at -3 and 4, which graph could represent function f?

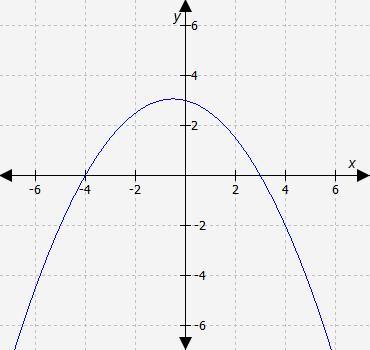


Answers
Answer:
first one
Step-by-step explanation:
The graph intersects x-axis at (4,0) and (-3,0)
If function f has zeros at -3 and 4 then the first graph represents the function f.
When a function has zeros at -3 and 4, it means that the function's value is equal to zero at those x-values.
In other words, when x = -3 and x = 4, the function f(x) becomes 0.
To represent this on a graph, you should look for two points where the graph intersects the x-axis at -3 and 4.
When the graph crosses the x-axis at these points, it indicates that the function has zeros at those x-values.
When we observe the graphs, the first graph has zeros at -3 and 4.
Hence, the first graph could represent the function f with zeros at -3 and 4.
To learn more on Functions click:
https://brainly.com/question/30721594
#SPJ4
i'm really confused, usually i'm good with this stuff but this is confusing :/



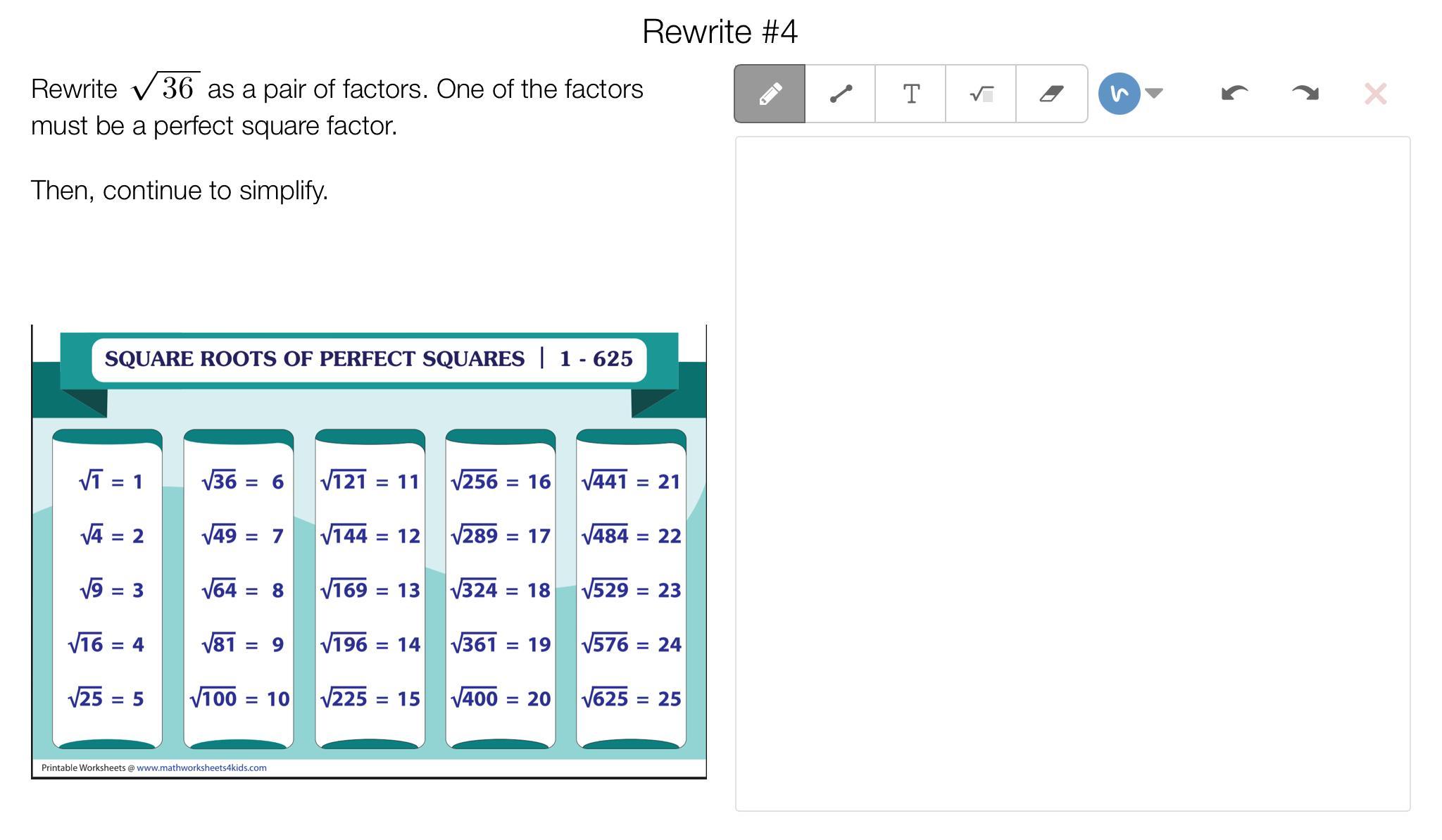
Answers
Rewrite 3:
/45
We know that one pair of factors of 45 is 9 and 5. 9 is a perfect square— 3x3. Therefore, you will write it as 3/5
The number inside the sign cannot be squared in a while number while the number outside is already squared.
So you will rewrite inside the radical sign 9 • 5. To simplify it, you will find the square root of the perfect square. 3 *radical sign* 5
I hope that makes sense, feel free to shoot me a message if you’re confused. I’ll write the rest of the answers down below. Again, I will use / as the radical sign and rewrite 3 to make it easier.
Rewrite 3
/45
= /9•5
= /3•3•5
= 3/5
Rewrite 2
/28
= /4•7
= /2•2•7
= 2/7
Rewrite 1
/20
= /4•5
= /2•2•5
= 2/5
Rewrite 4
/36
= /6•6
= 6
^— This one is different because 36 is already a perfect square. 6•6=36
I had written out the multiplications of the squares because that was the way we were taught. We would cross out the same numbers and then write it outside the radical sign. Hope that helps :)
What distance did the bus travel???

Answers
Answer:
495km
Step-by-step explanation:
180 km in 4 hours means x km in 11 hours.
Cross multiply and you'll find x as 495 km
On a coordinate plane, 2 triangles are shown. Triangle D E F has points (6, 4), (5, 8) and (1, 2). Triangle R S U has points (negative 2, 4), (negative 3, 0), and (2, negative 2).
Triangle DEF is reflected over the y-axis, and then translated down 4 units and right 3 units. Which congruency statement describes the figures?
ΔDEF ≅ ΔSUR
ΔDEF ≅ ΔSRU
ΔDEF ≅ ΔRSU
ΔDEF ≅ ΔRUS
Answers
The congruency statement that describes the figures is:
ΔDEF ≅ ΔRSU
To answer your question, let's first find the image of triangle DEF after reflecting over the y-axis and then translating down 4 units and right 3 units.
1. Reflect ΔDEF over the y-axis:
D'(−6, 4), E'(−5, 8), F'(−1, 2)
2. Translate ΔD'E'F' down 4 units and right 3 units:
D''(−3, 0), E''(−2, 4), F''(2, −2)
Now, we have ΔD''E''F'' with points (−3, 0), (−2, 4), and (2, −2). Comparing this to ΔRSU with points (−2, 4), (−3, 0), and (2, −2), we can see that:
ΔD''E''F'' ≅ ΔRSU
To learn more about : congruency statement
https://brainly.com/question/30534292
#SPJ11

Answer:
ΔDEF ≅ ΔRSU
Step-by-step explanation:
3 Simplify 3e - e + 4e
Answers
Step 6 1- - cos(x) After applying L'Hospital's Rule twice, we have lim X-0 48x2 The derivative of 1 cos(x) with respect to x is sin(x) The derivative of 48x2 with respect to x is 96x ✓ 96x Step 7 Since the derivative of 1 - cos(x) is sin(x) and the derivative of 48x² is 96x, sin(x) 1 - cos(x) lim X-0 48x² = lim x-0 96x Analyzing this we see that as x→ 0, sin(x) → 0 and 9 0 Step 8 After applying L'Hospital's Rule three times, we have lim So, we still 1 The derivative of sin(x) with respect to x is 96 The derivative of 96x with respect to x is 1 96 sin(x) x-0 96x X . x So, we still sin(x 1- cos(x) So, we still have an indeterminate limit of type T We will apply L'Hos lim X→0 48x² s sin(x) sin(x) 96x the derivative of 48x² is 96x, applying L'Hospital's Rule a third time gives us the follow 0 and 96x → 0 0 sin(x) ve have lim . So, we still have an indeterminate limit of type. We will apply L'H 1 96 6 x-0 96x X bly L'Hospital's Rule for a third time. To do so, we need to find additional derivatives. the following. I apply Hospital's Rule for a fourth time. To do so, we need to find additional derivatives.
Answers
Therefore, The limit of the given function is evaluated using L'Hospital's Rule repeatedly. The final answer is 1.
Explanation:
The given problem involves finding the limit of a function as x approaches 0. To evaluate the limit, L'Hospital's Rule is applied repeatedly to simplify the function. The derivative of 1-cos(x) with respect to x is sin(x), and the derivative of 48x² with respect to x is 96x. Using these derivatives, the limit is reduced to an indeterminate form of 0/0, which is resolved by applying L'Hospital's Rule again. This process is repeated multiple times until a final expression for the limit is obtained. The final answer is that the limit is equal to 1.
Therefore, The limit of the given function is evaluated using L'Hospital's Rule repeatedly. The final answer is 1.
To know more about function visit :
https://brainly.com/question/11624077
#SPJ11
marcos is planning to travel from phoenix to flagstaff. let t represent the number of hours since marcos left phoenix and let d represent the number of miles marcos has traveled from phoenix.
Answers
In this scenario, Marcos is planning to travel from Phoenix to Flagstaff, and we are using variables to represent different aspects of his journey.
The variable t represents the number of hours since Marcos left Phoenix, which serves as a measure of time elapsed since the start of the journey. It allows us to track the progress of Marcos over time and analyze various time-related aspects such as the duration of the journey or the rate at which he is traveling. On the other hand, the variable d represents the number of miles Marcos has traveled from Phoenix. It serves as a measure of distance covered, indicating how far Marcos has progressed on his route. By monitoring the value of d, we can determine the distance remaining to reach Flagstaff or calculate other distance-related parameters such as average speed or total distance traveled.
By using these variables, we can establish a relationship between time and distance traveled by Marcos. This relationship can be represented by a function or equation that describes Marcos' progress over time, such as a velocity equation or a distance-time equation. These variables and their relationship allow us to analyze and make predictions about Marcos' journey. We can determine when he is expected to reach certain milestones, calculate his average speed or rate of travel, and estimate the time required to complete the journey. Additionally, these variables provide a framework for solving various problems or making decisions related to Marcos' travel, such as optimizing his route or estimating fuel consumption based on distance traveled.
In summary, by using the variables t and d to represent time and distance traveled, respectively, we can effectively describe and analyze Marcos' journey from Phoenix to Flagstaff, enabling us to make informed decisions and predictions about his travel experience.
Learn more about variables here: brainly.com/question/32263664
#SPJ11
2. if a cylinder has a volume of 2908.33 in^3 and a radius of 11.5 in. what is the height of the cylinder
Answers
Answer:
\(\huge\boxed{\sf h \approx 7\ in}\)
Step-by-step explanation:
Given:Volume = V = 2908.33 in³
Radius = r = 11.5 in.
π = 3.14
To find:Height = h = ?
Formula:\(V= \pi r^2 h\)
Solution:Put the given data in the above formula.
2908.33 = (3.14)(11.5)²(h)
2908.33 = (3.14)(132.25)(h)
2908.33 = 415.265 (h)
Divide both sides by 415.2652908.33/415.265 = h
h ≈ 7 in\(\rule[225]{225}{2}\)
What is
-5 = m + 11 ?
Answers
Answer:
-16
Step-by-step explanation:
-16+11=-5 that's it lol
Answer:
m= -16
Step-by-step explanation:
subtract 11 from both sides
-5 - 11 =m + 11 - 11
combine like terms (-5 - 11 and 11 - 11)
m= -16
quiz 8-1 pythagorean theorem, special right triangles
14 and 16.

Answers
14.
x is equal to y because they have the same angle 45 degrees.
a²+b²=c²
x²+x²=6²
a = 4.24
b = 4.24
16.
x = 27.71
y = 13.85
z = 24
14) The values of x and y for the right triangle are \(3\sqrt{2}\).
15) The values of x, y, and z for the right triangle are \(x=8\sqrt{3}\), \(y=16\sqrt{3}\), and \(z=24\).
Given are right triangles.
14) Here, the length of the hypotenuse is 6.
It is required to find the length of the two legs.
The angle opposite the hypotenuse is 90°.
Another angle = 45°.
So, by the angle sum property of triangles, the third angle is also 45°.
So, the sides opposite these angles will be equal.
So, x = y.
By the Pythagorean theorem:
\(\sqrt{x^2+y^2} =6\)
Since x = y,
\(\sqrt{2x^2} =6\)
Square both sides.
\(2x^2=36\)
Divide both sides by 2.
\(x^2=18\)
Take the square root on both sides.
\(x=3\sqrt{2}=y\)
15) There are two right triangles given.
Consider the right triangle on the left.
Hypotenuse = \(24\sqrt{2}\).
Let m denote the unnamed side of this triangle which is common to both right triangles.
Since one of the angles is 45°, the other is also 45°.
So, m = z.
So, using the Pythagorean theorem:
\(2z^2=(24\sqrt{2} )^2\)
\(2z^2=1152\)
Divide both sides by 2.
\(z^2=576\)
Take the square root on both sides.
\(z=24\)
From the other triangle, using the angle sum property, the third angle = 30°.
The side opposite 60° = z = 24.
The ratio of the sides for the 30°-60°-90° triangle is 1 : √3 : 2.
Here, \(\sqrt{3} x=24\).
So, \(x=8\sqrt{3}\).
And, \(y=2x\).
So, \(y=16\sqrt{3}\).
Hence the values of x and y are \(3\sqrt{2}\) for the first one, and the values of \(x=8\sqrt{3}\), \(y=16\sqrt{3}\), and \(z=24\).
Learn more about Pythagorean Theorem here :
https://brainly.com/question/14930619
#SPJ6
Resolve the expression \(\frac{(x-2)}{(x^{2} +1)(x-1)^{2} }\) into the simplest partial fractions
Answers
The partial fraction expansion will look like
(x - 2)/((x ² + 1) (x - 1)²) = (ax + b)/(x ² + 1) + c/(x - 1) + d/(x - 1)²
Get everything in terms of a common denominator, and compare the numerators on both sides:
x - 2 = (ax + b) (x - 1)² + c (x ² + 1) (x - 1) + d (x ² + 1)
Expand the right side:
x - 2 = (ax + b) (x - 1)² + c (x ² + 1) (x - 1) + d (x ² + 1)
x - 2 = (a + c) x ³ + (-2a + b - c + d) x ² + (a - 2b + c) x + b - c + d
Match up the coefficients and solve the resulting system of equations:
a + c = 0
-2a + b - c + d = 0
a - 2b + c = 1
b - c + d = -2
==> a = -1, b = -1/2, c = 1, d = -1/2
So the expansion into partial fractions is
(x - 2)/((x ² + 1) (x - 1)²) = (-x - 1/2)/(x ² + 1) + 1/(x - 1) - 1/(2 (x - 1)²)
… = -(2x + 1)/(2 (x ² + 1)) + 1/(x - 1) - 1/(2 (x - 1)²)
The rate at which rainwater flows into a drainpipe is modeled by the function R, where R(t)=20sin(t^2/35) cubic feet per hour, t is measured in hours, and 0 ≤ t ≤ 8. The pipe is partially blocked, allowing water to drain out the other end of the pipe at a rate modeled by D(t) = -0.04t3 + 0.4t2 + 0.96t cubic feet per hour, for 0 ≤ t ≤ 8. There are 30 cubic feet of water in the pipe at time t = 0. (a) How many cubic feet of rainwater flow into the pipe during the 8-hour time interval 0 ≤ t ≤ 8?
Answers
There are 30 cubic feet of water in the pipe at time t = 0. 76.570 cubic feet of rainwater flow into the pipe during the 8-hour time interval 0 ≤ t ≤ 8.
\(\int\limits^8_0\) [R(t) dt = \(\int\limits^8_0\) 20 sin \(\frac{t^2}{35}\) dt = 76.570
What Is Time Interval?
The amount of time between two given times is known as time interval. In other words, it is the amount of time that has passed between the beginning and end of the event. It is also known as elapsed time.
INTERVAL types are divided into two classes: year-month intervals and day-time intervals. A year-month interval can represent a span of years and months, and a day-time interval can represent a span of days, hours, minutes, seconds, and fractions of a second.
Learn more about time interval from brainly, visit: brainly.com/question/15848206
#SPJ4
9/4 is close to the square root of what integer
Answers
The integer whose square root is close to 2.25 is 5, and the correct answer is √5 ≈ 9/4.
The given equation is 9/4 = 2.25, which is equivalent to saying that 2.25 is close to the fraction 9/4.
We can use this information to find an integer whose square root is close to 2.25.
Let's check the square root of some integers to see which one is closest to 2.25:
√1 ≈ 1.00
√2 ≈ 1.41
√3 ≈ 1.73
√4 ≈ 2.00
√5 ≈ 2.24
√6 ≈ 2.45
√7 ≈ 2.65
√8 ≈ 2.83
√9 ≈ 3.00
As we can see, the square root of 5, √5 ≈ 2.24, is the closest integer to 2.25.
So, the integer whose square root is close to 2.25 is 5, and the correct answer is √5 ≈ 2.24.
To learn more on square root click:
brainly.com/question/29286039
#SPJ7
23 people attend a party. Each person shakes hands with at least two other people. What is the minimum possible number of handshakes
Answers
The minimum possible number of handshakes would occur if each person only shakes hands with two other people. In this case, the first person would shake hands with the second and third person, the second person would shake hands with the first and fourth person, the third person would shake hands with the first and fifth person, and so on. This pattern would continue until the 22nd person shakes hands with the 21st and 23rd person, and the 23rd person shakes hands with the 22nd and 21st person. Therefore, the minimum possible number of handshakes would be (23-1) or 22 handshakes.
Hi! To find the minimum possible number of handshakes among the 23 people attending the party, we need to ensure that each person shakes hands with at least two other people. Here's a step-by-step explanation:
1. Have the first person shake hands with two other people. This results in 2 handshakes.
2. For each subsequent person, have them shake hands with the two people that the previous person shook hands with.
Following this pattern, the first person will have 2 handshakes, and the remaining 22 people will each contribute 1 additional handshake, making a total of 22 handshakes.
So, the minimum possible number of handshakes among the 23 people at the party is 22 handshakes.
To know more about probability visit:
https://brainly.com/question/13604758
#SPJ11
Which statement is true regarding the functions on the
graph?
f(2) = g(2)
f(0) = g(0)
f(2) = g(0)
f(0) = g(2)

Answers
Answer:
Im pretty sure its f(0) = g(0)
Step-by-step explanation:
did i get these questions right??? please help! this is 15% of my grade !!!!

Answers
Answer:
yes you got it correct smart
Step-by-step explanation:
Use Elimination to solve the system below, find X and Y and answer as ( x , y )
2x + y = 19
x - y = 11
Answers:
( -1 , 10 )
( 10 , -1 )
( 1 , 10 )
( 10 , 1 )
Answers
11 1 point Solve for the measure < PZQ: RO 120⁰ Ze 170⁰ Type your answer...

Answers
The measure of angle PZQ is equal to 70°.
What is a circle?In Mathematics, a circle can be defined as a closed, two-dimensional curved geometric shape with no edges or corners. Additionally, a circle refers to the set of all points in a plane that are located at a fixed distance (radius) from a fixed point (central axis) with a measure of 360 degrees.
Generally speaking, the sum of all the angles around a point is equal to one full turn, which makes it equal to 360 degrees;
m∠PZR + m∠QZR + m∠PZQ = 360
120 + 170 + m∠PZQ = 360
290 + m∠PZQ = 360
m∠PZQ = 360 - 290
m∠PZQ = 70°.
Read more on angle here: https://brainly.com/question/24024505
#SPJ1
11. Let X 1 ,…,X n,…∼iidBeta(1,β) and let Y n = 1≤i≤n min X i and Z n = 1≤i≤n
max Xi be the sample minimum and maximum of the first n observations. (a) Find the value b such that Yn → pb.
Answers
Therefore , the solution of the given problem of probability comes out to be -y^(β-1)/[(β-1)Β(1, β)] .
What is probability exactly?The primary goal of the structures in the style known as parameters is the determination of the likelihood that a claim is accurate or that a specific event will occur. Any number between 0 and 1, at which 1 typically denotes certainty but also 0 typically denotes potential, can be used to symbolise chance. A probability diagram shows the chance that a specific event will occur.
Here,
We are aware that X's PDF is provided by:
If x is between 0 and 1 and 0 otherwise, f(x) Equals 1/B
where represents the size factor.
The formula for Yn's cumulative distribution function (CDF) is
=> F(y) = P(Yn ≤ y) = [P(Xi > y)]ⁿ = [1 - P(Xi ≤ y)]ⁿ
Using the CDF of the beta distribution, we have:
=> F(y) = [1 - Β(1, β; y)]ⁿ
We can approximate Yn by a normal distribution with mean and variance given by the following formulas using the continuity adjustment and central limit theorem:
=> E(Yn) = Β(2, β; 1)/Β(1, β) and Var(Yn) = E(Yn) - [Β(1, β; 1)/Β(1, β)]²
Therefore, we have:
=> (Yn - E(Yn))/sqrt(Var(Yn)) → N(0,1)
With the formulas for E(Yn) and Var(Yn) substituted, we obtain:
=> (Yn - Β(2, β; 1)/Β(1, β))/sqrt[Β(2, β; 1)/Β(1, β) - [Β(1, β; 1)/Β(1, β)]²] → N(0,1)
We need to work out the solution to determine b:
where is the CDF's usual standard value.
After applying the limit and taking the logarithm of both sides, we obtain:
=> F(y) = lim n log[n] = lim n n log
=> [1 - B(1, β; y)] = lim n -n (y, n)/(1, n)
L'Hopital's law gives us:
=> lim n -d/dy [n -(1, y)/n -(1, y)] = lim nn y(-1), ((1, )) ^2Β(2, β; y)
=> -y^(β-1)/[(β-1)Β(1, β)]
To know more about probability visit:
https://brainly.com/question/11234923
#SPJ1
a right triangle has a height of 27 inches and a base of 30 inches what is the area of the triangle
Answers
Answer:
The answer is 405
Step-by-step explanation:
FIrst you would do 27 times 30 which is 810 then you would divided by 2 which in turn gives you 405
Hope this helped!
an opinion poll on a political issue is taken by a campaign. out of 400 respondents, 210 support issue 1, others are against issue 1. there is a belief that the support of the issue 1 is different from the majority. find the p-value for this situation.
Answers
p-value < 0.0001, reject null hypothesis. Proportion of supporters for issue 1 is significantly different from the majority.
To find the p-an incentive for this present circumstance, we really want to direct a speculation test. We should expect the invalid speculation is that the extent of allies for issue 1 is equivalent to the larger part, and the elective theory is that the extent of allies is not the same as the larger part.
Utilizing a two-followed z-test with an importance level of 0.05, we can work out the z-measurement as:
z = (210/400 - 0.5)/sqrt(0.5 * 0.5/400) = 4.14
The p-an incentive for this test is the likelihood of getting a z-score more noteworthy than 4.14 or not exactly - 4.14, which is tiny (under 0.0001). In this way, we can dismiss the invalid speculation and presume that there is sufficient proof to propose that the extent of allies for issue 1 is altogether not quite the same as the larger part.
To learn more about p-value, refer:
https://brainly.com/question/18523022
#SPJ4
Simplify square root of 250 times Square root of 2
Answers
Answer:
Step-by-step explanation:
22.36067977
what is the answer to 15-2x=-7x= solve for x
Answers
Answer:
-3 is what I got
Step-by-step explanation:
The frog population in a small pond grows exponentially. The current population is 85 frogs and the population grows by 18% each year.
A: Find a function that models the number of frogs after t years.
B: Find the number of years for the frog population to reach 600.
Answers
Answer: Your equation is y=85(1.18)^x and it will take a little under 12 years for the population to reach 600.
Step-by-step explanation:
The equation for an exponential equation is y=ab^x
Change 18% to a decimal and than add 1 to it because it has to be above 1 to increase.
This is your equation ---> y=85(1.18)^x
After 11 years, the population of the frogs would be 525 and for 12 years, the population will be 619. So for the population to reach 600, it will take a little under 12 years.
Len bought 12.3 ounces of cashews and 15.2 ounces of almonds.
He calculates that if he and four friends share all the nuts equally,
each person will receive 5.1 ounces of nuts.
Which is the best explanation for whether or not his answer is reasonable?
A. Not reasonable; 12.3 + 15.2 = 25.5 and 25.5 ÷ 5 = 4.5.
B. Not reasonable; 12.3 + 15.2 = 27.5 and 27.5 ÷ 5 = 5.5.
C. Reasonable; 12.3 + 15.2 = 27.5 and 27.5 ÷ 5 = 5.1.
D. Reasonable; 12.3 + 15.2 = 25.5 and 25.5 ÷ 5 = 5.1.
Answers
Answer:
B
Step-by-step explanation:
Total ounces of nuts is cashews (12.3 ounces) plus almonds (15.2 ounces) is 27.5 ounces. If you divide 27.5 ounces by 5 people, 27.5 / 5 = 5.5 ounces each.