The first term of an arithmetic sequence is six. The fifth term of the sequence is -14. th Write a rule that can be used to find the nth term.
Answers
Answer:
\(a_{n} = 11 - 5n\)
Step-by-step explanation:
use the formula
\(a_{n} = a_{1} + (n - 1)d\)
-14 = 6 + (5 - 1)d
-14 = 6 + 4d
-20 = 4d
d = -5
\(a_{n} = 6 + (n - 1)(-5) = 6 - 5n + 5 = 11 - 5n\)
Related Questions
PLEASE HELP ASAP!! 30 POINTS FOR ANSWERS!!

Answers
Answer:
Step-by-step explanation:
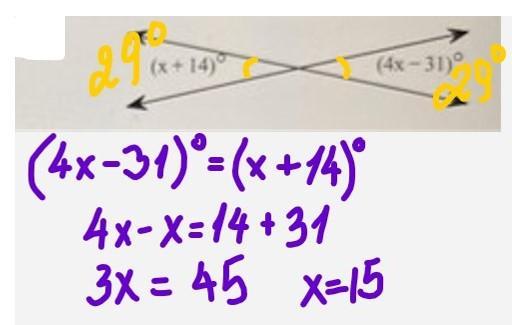
4x-18=x-3 will give ten points for answer asap
Answers
Answer: x=5
Good luck :)
Solve for a side in right triangles

Answers
Answer:
? = 7.45
Step-by-step explanation:
Since this is a right triangle, we can use trig functions
cos theta = adjacent side/ hypotenuse
cos 20 = 7 / ?
Multiply each side by ?
? cos 20 = 7
Divide each side by cos 20
? = 7/ cos 20
? =7.449244407
To the nearest hundredth
? = 7.45
Answer:
7.45 units
Step-by-step explanation:
\(\cos 20\degree = \frac{BC}{AB}\\\\0.939692620 = \frac{7}{AB}\\\\AB = \frac{7}{0.939692620}\\AB = 7.4492\\AB = 7.45 units\)
The water dam is filled up using the first tributary in 1 hour and 10 minutes, using the second
tributary in 60 minutes. How many minutes it takes to fill the half of the dam using both of the
tributaries, if the second tributary will be opened 12 minutes after the first one ?
Answers
Answer:
I would use quaro is is faster.
Step-by-step explanation:
ASAP!!! ITS URGENT
Find the lateral areas and total areas of these right rectangular or triangular prisms.

Answers
The Lateral Area and Total Area of the given shapes are:
2)
LA = 2040cm²
TA = 6360cm².
3)
LA = 324m
TA = 351m
4)
LA = 1000cm²
TA = 3232cm²
5)
LA = 124.71 cm²
TA = 155.90 cm²
What is the calculation for the above?
2) The lateral area of a cuboid is the combined surface area of all the sides of the cuboid excluding the top and bottom faces.
The total surface area of a cuboid is the sum of the lateral area and the area of the top and bottom faces.
To calculate the lateral area of the given cuboid, we need to add the areas of the four lateral faces:
Lateral Area = 2 x Length x Height + 2 x Breadth x Height
Lateral Area = 2 x 38cm x 15cm + 2 x 30cm x 15cm
Lateral Area = 1140cm² + 900cm²
Lateral Area = 2040cm²
To calculate the total surface area of the cuboid, we need to add the area of the top and bottom faces as well:
Total Area = Lateral Area + 2 x Length x Breadth + 2 x Length x Height + 2 x Breadth x Height
Total Area = 2040cm² + 2 x 38cm x 30cm + 2 x 38cm x 15cm + 2 x 30cm x 15cm
Total Area = 2040cm² + 2280cm² + 1140cm² + 900cm²
Total Area = 6360cm²
Therefore, the lateral area of the given cuboid is 2040cm², and the total surface area of the cuboid is 6360cm².
3)
LA = P (L*W)
= (Side 1 + Side 2 + Side 3) (L*W)
= (4m+ 3m + 5m) (9*3)
LA = 324m
TA = P(L*W) + 2(L*W)
TA = (11 (27)) + 2(27)
TA = 321m
4)
The lateral area of a cuboid is the combined surface area of all the sides of the cuboid excluding the top and bottom faces.
The total surface area of a cuboid is the sum of the lateral area and the area of the top and bottom faces.
To calculate the lateral area of the given cuboid, we need to add the areas of the four lateral faces:
Lateral Area = 2 x Length x Height + 2 x Breadth x Height
Lateral Area = 2 x 28cm x 10cm + 2 x 22cm x 10cm
Lateral Area = 560cm² + 440cm²
Lateral Area = 1000cm²
To calculate the total surface area of the cuboid, we need to add the area of the top and bottom faces as well:
Total Area = Lateral Area + 2 x Length x Breadth + 2 x Length x Height + 2 x Breadth x Height
Total Area = 1000cm² + 2 x 28cm x 22cm + 2 x 28cm x 10cm + 2 x 22cm x 10cm
Total Area = 1000cm² + 1232cm² + 560cm² + 440cm²
Total Area = 3232cm²
Therefore, the lateral area of the given cuboid is 1000cm², and the total surface area of the cuboid is 3232cm².
5)
To find the lateral area, we need to find the area of all the rectangular faces and add them together. The area of each rectangular face is:
Area = length x height = 6 cm x (4√3 cm) = 24√3 cm².
Area ≈ 41.57 cm².
There are three rectangular faces, so the total lateral area is:
Lateral area = 3 x 41.57 cm². ≈ 124.71 cm²
To find the total area, we need to add the area of the two equilateral triangles to the lateral area. The area of each equilateral triangle is:
Area = (√3 / 4) x base² = (√3 / 4) x 6² = 9√3 cm²
Area ≈ 15.59 cm²
There are two equilateral triangles, so the total area of both triangles is:
Total area of both triangles = 2 x 15.59 cm² ≈ 31.19 cm².
Therefore, the total area of the prism is:
Total area = lateral area + total area of both triangles
Total area ≈ 124.71 cm² + 31.19 cm² ≈ 155.90 cm²
So, the lateral area of the prism is approximately 124.71 cm² and the total area is approximately 155.90 cm²
Learn more about Lateral Areas:
https://brainly.com/question/14001755
#SPJ1
6. The quadratic functions f(x) =-x+2x+6 and g(x)= x’ +2x are shown graphed below. The positivesolution to f(x)=g(x) is closest to which of the following?Y(1) x=6.5(3) x=1.7(2) x = 3.7(4) x=0.5
Answers
Notice that the intersection between both functions on the positive values of x is near the line x=2. From the provided options, the closest to that value is 1.7
Then, the positive solution to f(x)=g(x) is closest to:
\(x=1.7\)Brainliest if correct!_A particle is projected vertically upwards from a fixed point O. The speed of projection is u m/s. The particle returns to O 4 seconds later. Find:
a) the value of u
b) the greatest height reached by the particle
c) the total time of which the particle is at a height greater than half its greatest height
Thank you so much!
Answers
The value of the velocity, u is 19.6 m/s.
The greatest height reached by the particle is 19.6 m.
The total time during which the particle is at a height greater than half its greatest height is 2.33 s.
What is the value of the velocity, u?a) To find the value of the velocity, u, we can use the formula for the time of flight of a vertically projected particle:
t = 2u/g
Since the particle returns to the same point after 4 seconds, we have:
2t = 4
Substituting the value of t in the first equation, we get:
u = gt/2 = 9.8 x 2
u = 19.6 m/s
b) To find the greatest height reached by the particle, we can use the formula for the maximum height reached by a vertically projected particle:
h = u^2/2g
Substituting the value of u, we get:
h = 19.6^2/(2 x 9.8)
h = 19.6 m
c) To find the total time during which the particle is at a height greater than half its greatest height, we can first find the height at which the particle is at half its greatest height:
h/2 = (u^2/2g)/2 = u^2/4g
Substituting the value of u, we get:
h/2 = 19.6^2/(4 x 9.8) = 24.01 m
So, the particle is at a height greater than half its greatest height when it is above 24.01 m.
Next, we can find the time taken by the particle to reach this height:
h = ut - (1/2)gt^2
24.01 = 19.6t - (1/2)9.8t^2
Solving this quadratic equation, we get:
t = 2.33 s or t = 4.10 s
The particle takes 2.33 s to reach a height of 24.01 m, and it takes another 1.67 s (4 - 2.33) to return to the ground.
Learn more about velocity at: https://brainly.com/question/80295?source=archive
#SPJ1
You have torn a tendon and is facing surgery to repair it. The surgeon explains the risks to you: infection occurs in 4%4% of such operations, the repair fails in 12%,12%, and both infection and failure occur together in 2%.2%. What percentage of these operations succeed and are free from infection
Answers
The percentage of operations that succeed and are free from infection is 86%.
To determine the percentage of operations that succeed and are free from infection, we need to subtract the probabilities of infection and failure from 100%.
Infection occurs in 4% of the operations.
The repair fails in 12% of the operations.
Both infection and failure occur together in 2% of the operations.
Let's calculate the percentage of operations that succeed and are free from infection:
Percentage of operations with infection = 4%
Percentage of operations with failure = 12%
Percentage of operations with both infection and failure = 2%
Percentage of operations without infection = 100% - 4% = 96%
Percentage of operations without failure = 100% - 12% = 88%
Percentage of operations without infection and failure = 100% - (4% + 12% - 2%) = 86%
To know more about percentage:
https://brainly.com/question/16797504
#SPJ4
Emily wants to buy turquoise stones on her trip to New Mexico to give to at least 4 of her friends. The gift shop sells small stones for $4 and large stones for $6. Emily has $30 to spend.
a. write and graph a system of linear inequalities
b. write two possible solutions
Answers
Step-by-step explanation:
s for small stones
l for large
4s+6l<=30 (<= means less or equal to because I couldn't get the sign on here).
s+l>=4. (>= means greater than or equal to).
Possible Answers:
s+l=5 (if she bought 5 stones in total)
answer #1: 5 large stones and 0 small stones.
s+l=6 (if she bought 6 stones in total)
answer #2: 3 large stones and 3 small stones.
so sorry i couldn't do the graphing part...
The two possible solutions are; x = 5, y = 0 and x = 5, y = 1
What is Linear inequality?Linear inequalities are defined as a mathematical expression in which two expressions are compared using the inequality symbol.
Given that, Emily wants to buy turquoise stones on her trip to New Mexico to give to at least 4 of her friends. The gift shop sells small stones for $4 and large stones for $6. Emily has $30 to spend.
Let the number of $4 and $6 stones that Emily can buy be x and y respectively.
According to question,
Since, Emily wants to gift to at least 4 friends, so,
x + y ≥ 4 ............ (i)
Also, she can spend a maximum of $30 only,
4x + 6y ≤ 30 ............... (ii)
Studying graph we get solutions;
x = 5, y = 0
and x = 5, y = 1
Hence, The two possible solutions are; x = 5, y = 0 and x = 5, y = 1
For more references on Linear inequalities, click;
https://brainly.com/question/11897796
#SPJ2

1.) Solve the equation for y.
4x-5y=9
A.y= -4x-9
B.y= 5/4x+9/4
C.y= -5/4x-5/9
D.y= 4/5x-9/5
2. Which ordered pair in the form (a,b) is a solution of this equation?
7a-5b=28
A.(-3,-2)
B.(-2,-3)
C.(4,0)
D.(0,4)
3.Which of the ordered pairs in the form (x,y) is a solution of this equation?
5x-y/3=13 (2,-9),(3,-6)
A.Neither is a solution
B.The first is a solution, but the second is not
C. Both are solution
D. The first is not a solution, but the second is
4. Which ordered pair in the form (x,y) is a solution of this equation?
(x+3)y=14
A.(5,2)
B.(11,1)
C.(7,2)
D.(3,2)
5.)Which pair are solutions to the equation?
4xy+8=36
A.(1,7) and (7,1)
B.(7,1) and (3,2)
C.(4,9) and (3,2)
D.(1,7) and (4,9)
Answers
1. Correct option D. y= 4/5x-9/5
2. option C. (4, 0) is a solution.
3. option B, is the correct answer.
4. option B. (11, 1), is a solution.
5. option A, "(1,7) and (7,1)" is a correct answer.
Define the term equation?A statement proving the equality of two mathematical expressions is known as an equation.
1. Solve the equation for y: 4x - 5y = 9
⇒ 5y = 4x - 9
⇒ y = 4/5 x - 9/5 (correct option D)
2. Solution of this equation: 7a - 5b = 28
from the given options we simply substitute the values of a and b into the equation and check if the equation holds true.
option C. (4, 0);
Substituting a=4 and b=0 into the equation 7a-5b=28, we get:
7(4) - 5(0) = 28, which is equal to 28. So (4, 0) is a solution.
3. we simply substitute the values of x and y into the equation and check if the equation holds true.
Substituting x=2 and y=-9 into the equation 5x-y/3=13, we get:
5(2) - (-9)/3 = 10 + 3 = 13, which is equal to 13. So (2,-9) is a solution.
Substituting x=3 and y=-6 into the equation 5x-y/3=13, we get:
5(3) - (-6)/3 = 15 + 2 = 17, which is not equal to 13. So (3,-6) is not a solution.
Therefore, option B, "The first is a solution, but the second is not" is the correct answer.
4. we simply substitute the values of x and y into the equation and check if the equation holds true.
option B. (11, 1), Substituting x=11 and y=1 into the equation (x+3)y=14, we get: (11+3)(1) = 14(1) = 14, which is equal to 14. So (11,1) is a solution.
5. we substitute each pair into the equation and check if it holds true.
option A. (1,7) and (7,1); Substituting x=1 and y=7 into the equation 4xy+8=36, we get: 4(1)(7) + 8 = 28 + 8 = 36, which is equal to 36. So (1,7) is a solution.
Substituting x=7 and y=1 into the equation 4xy+8=36, we get:
4(7)(1) + 8 = 28 + 8 = 36, which is equal to 36. So (7,1) is also a solution.
Therefore, option A, "(1,7) and (7,1)" is a correct answer.
To know more about equation, visit:
brainly.com/question/2228446
#SPJ1
The answers of the given equations are
1. option D
2.option C
3. option B
4.option B
5.option A.
What is equation?
Equation is basically a mathematical statement where two expressions are connected by a equal sign. It contains atleast one variable that has be determined.
1) Given equation is 4x- 5y= 9
To solve this equation at first we subtract 4x from both sides
-5y= 9-4x
Multiplying by '-' sign to the both sides of the equation we get,
5y= 4x-9
Dividing by 5 on the both sides of equation we get,
y= (4/5)x - (9/5)
Hence option D is correct.
2) Given equation is 7a-5b = 28----------(1)
putting a=4 and b=0 in equation (1) we get,
7× 4- 5×0=28
Hence the ordered pair ( 4,0) is the solution of the equation as the value of a and b satisfies the right side of equation (1). option C.
3) Given equation is 5x- y/3= 13-----------(2)
Putting (2,-9) in equation (2) we get,
10+3=13 which is the RHS of equation (2)
Putting (3,-6) in equation (2) we get,
15+2=17 which is not the RHS of equation (2)
So the first is a solution of the equation but the second is not.
Option B.
4) Given equation is (x+3)y=14---------(3)
Putting the values (11,1) in equation (3) we get,
(11+3)×1= 14 which is the RHS of the equation (3).
So the ordered pair is (11,1).
Option B.
5) Given equation is 4xy+8=36
It can be deduced to,
4xy+8=36
4xy= 36-8
4xy= 28
x y= 7-------(4)
Putting (1,7) and (7,1) in equation (4) we get,
1×7=7×1=7 which is the RHS of equation (4)
So the pair is (1,7) and (7,1). Option A.
Hence, the answers are
1. option D
2.option C
3. option B
4.option B
5.option A.
To learn more about equation
https://brainly.com/question/2228446 from the link.
#SPJ1
what is the estimate of 3,182x5
Answers
Step-by-step explanation:
15,910 like what said of calculator
Using the digits 1 to 9 at most one time each fill in the boxes to create an equation that has a negative solution
[]x+[]=[]x+[]
Answers
Answer:
[4]x+[8]=[1×]+2
Step-by-step explanation:
x will be negative now that the more x you have the higher your number will have to be.
The requried, x is negative, the left-hand side of the equation is positive, but the right-hand side is negative, so the equation has a negative solution as x = -3.5.
What is simplification?The process in mathematics to operate and interpret the function to make the function or expression simple or more understandable is called simplifying and the process is called simplification.
Here,
One possible solution is,
[1]x + [2] = [3]x + [9]
To see that this equation has a negative solution, we can rearrange it to get:
x + 2 = 3x + 9
x - 3x = 9 - 2
-2x = 7
x = -3.5
Since x is negative, the left-hand side of the equation is positive, but the right-hand side is negative, so the equation has a negative solution.
Learn more about simplification here:
https://brainly.com/question/12501526
#SPJ2
4) Haleakela is a 10,000 foot high dormant volcano on Maui, Hawaii. The peak is a horizontal distance of 30,000 feet from the ocean. At what angle would you have to look up to see the peak if you were standing at the edge of the ocean?
Answers
ITS 67 dgrees Step-by-step explanation: NP BRAINLIEST OR NA :)?
The angle that you would have to look up to see the peak if you were standing at the edge of the ocean is 18.4°.
Angle:Let x represent the angle
Tan x=Height/Horizontal distance
Tan x =10,000/30,000
x=Tan^-1 (1/3)
x=18.4°
Inconclusion the angle that you would have to look up to see the peak if you were standing at the edge of the ocean is 18.4°.
Learn more about angle here:https://brainly.com/question/25770607
E is inversely proportional to F3.
Select the correct formula connecting E and F.
• E = kĖ
OE E = KF31
ke
Ο Ε
F13
OE =
k
F
h
Submit Answer
Skip for Now
о
H
Answers
The formula connecting E and F is E = k/F3, where k is a constant. This formula states that the value of E is inversely proportional to the cube of F.
That is, as F increases, the value of E decreases. For example, if F increases from 3 to 4, then the value of E decreases by a factor of 8.
This inverse proportionality between E and F3 is due to the fact that, as F increases, the cube of F increases at a faster rate. In other words, when F doubles, the cube of F increases by a factor of 8. This causes the value of E to decrease by the same factor of 8.
The formula is useful in many applications, such as in physics and engineering. For example, in physics, the formula can be used to calculate the force of an object in a gravitational field. The force is inversely proportional to the cube of the distance between the object and the center of gravity, where the constant k is equal to the gravitational constant. In engineering, the formula can be used to calculate the power of a motor, where the power is inversely proportional to the cube of the speed of the motor.
Overall, the formula E = k/F3 expresses the inverse proportionality between E and F3, and is used in various applications to calculate the value of E given the value of F.
Learn more about inversely proportional here:
https://brainly.com/question/28747940
#SPJ4
Which of the statements about the y-axis are true? I.The y-axis is a vertical number line that passes through the origin.II.The y-axis intersects the x-axis at the point (0 , 0).III.The y-axis is the first coordinate in an ordered pair that describes the vertical distance from the origin.IV.The y-axis is a horizontal number line that passes through the origin.
Answers
Answer:
No i does not well it will be 0,5 or any other number but the x wont change
Step-by-step explanation:
Graph each inequality and graph its solution.
3) n - 11 > -21
Answers
Inequality: n>-10
Interval Notation: (-10,infinity)
On Monday, Duncan skateboard shop received its first shipment of skateboards. Duncan sold 12 skateboards that day. On Thursday, he sold 9 skateboards. On Friday, he received a shipment of 30 more skateboards and sold 10 skate boards. He then had a total of 32 skateboards in a shop. How many skateboards were delivered on Monday?
Answers
Answer:
33
Step-by-step explanation:
find (f+g) (×) and (f-g) (×) and state the domain for each. then evaluate f+g and f-g for the given value of x

Answers
By answering the presented question, we may conclude that Therefore, domain (f+g)(-2) = 17 and (f-g)(-2) = 31.
what is domain?The domain of a function is the range of possible values that it can accept. These numbers represent the x-values of a function such as f. (x). The domain of a function is the range of possible values that can be used with it. This set includes the value returned by the method after adding the x value. A function with y as the dependant variable and x as the independent variable has the formula y = f. (x). When a single value of y can be created successfully from a value of x, that value of x is said to be in the function's domain.
To find (f+g)(x) and (f-g)(x), we need to add and subtract the two functions, respectively, and evaluate the resulting expressions at x.
\((f+g)(x) = f(x) + g(x) = (x^2 - 6x + 8) + (x - 5) = x^2 - 5x + 3\\(f-g)(x) = f(x) - g(x) = (x^2 - 6x + 8) - (x - 5) = x^2 - 7x + 13\\(f+g)(-2) = (-2)^2 - 5(-2) + 3 = 4 + 10 + 3 = 17\\(f-g)(-2) = (-2)^2 - 7(-2) + 13 = 4 + 14 + 13 = 31\\\)
Therefore, (f+g)(-2) = 17 and (f-g)(-2) = 31.
To know more about domain visit:
https://brainly.com/question/28135761
#SPJ1
Plz plz plz plz help

Answers
Answer:
AC is 6.5 cm
Step-by-step explanation:
From trigonometric ratios:
\( \sin( \theta) = \frac{opposite}{hypotenuse} \\ \)
opposite » 3 cm
hypotenuse » AC
angle » 28°
\( \sin(28 \degree) = \frac{3}{AC} \\ \\ AC = \frac{3}{ \sin(28 \degree) } \\ \\ AC = \frac{3}{0.46} \\ \\ AC = 6.5 \: cm\)
Answer:
Here sin28 = perpendicular/hypotenuse
AC = sin28 * 3
AC = 0.46*3
AC = 1.38
f. if a is an m n matrix whose columns do not span rm, then the equation ax d b is inconsistent for some b in rm.
Answers
The statement ''f. if a is an m n matrix whose columns do not span rm, then the equation ax d b is inconsistent for some b in rm '' is TRUE.
Let us assume that a is an m x n matrix that doesn't span rm. It means that the columns of a matrix don't contain all the vectors in the m-dimensional vector space that a is associated with. Therefore, it is not possible to find the linear combination of the columns of a that produces some vectors in rm.
We can also say that a matrix is inconsistent when there is no solution possible for the given linear equation. A system of linear equations is inconsistent when it has no solution.To prove the statement f, we need to prove that if a matrix doesn't span rm, then the given equation ax = b is inconsistent for some b in rm.
Here is a proof:
Let's assume that the columns of the matrix a don't span rm. It means that some vector in rm is not in the column space of a matrix.
Let's assume that vector is v.
Now, let's consider the linear equation ax = v. Since v is not in the column space of matrix a, there is no solution to this equation. It means that the equation ax = v is inconsistent.
Hence, we can say that the statement f. if a is an m n matrix whose columns do not span rm, then the equation ax d b is inconsistent for some b in rm is true
Learn more about matrix at
https://brainly.com/question/29132693
#SPJ11
Help needed ASAP
Please answer without rounding if you need to round

Answers
Answer:
you dont need to round
Step-by-step explanation:
multiply v and U and then add the other numbers and that should work
Answer:
\(\huge\boxed{\sf r = 37\ mm}\)
Step-by-step explanation:
Let the radius be r
UV is tangent to the circle T which means UV is perpendicular to UT, that makes ΔUVT a right-angled triangle.
Which means:
∠TUV = 90°
So, We can use pythagoras theorem to find the radius of the circle.
In the Δ:
Hypotenuse = r + 9
Base = r
Perpendicular = 12
Pythagoras Theorem:
(Hypotenuse)² = (Base)² + (Perpendicular)²
(6 + r)² = (r)² + (22)²
(6)² + 2(6)(r) + (r)² = r² + 484
36 + 12r + r² = r² + 484
Subtract r² to both sides
36 + 12r = 484
Subtract 36 to both sides
12r = 484 - 36
12r = 448
Divide both sides by 12
r = 448/12
r = 37 mm
\(\rule[225]{225}{2}\)
in a distribution with a mean of 100 and a standard deviation of 15, what is the probability that the score will be 120 or higher
Answers
0.0912 is the probability that the score will be 120 or higher .
What is probability explain with an example?
The likelihood that something will occur is the foundation of it. The justification for probability serves as the basic foundation for theoretical probability. A coin is tossed, for instance, and the theoretical likelihood of getting a head is 1 in 2.Zlower = X₁ - μ/σ = 120 - 100/15 = 1.33
the probability is compared as
Pr ( X ≥ 120 ) = Pr(X - 100/15 ≥ 120 - 100/15)
= Pr(Z ≥ 120 - 100/15
= Pr( Z ≥ 1.33)
= 0.0912
Since 0.0912 > 0.05 i.e. this IQ score is not unusual and hence I can believe the claim.
Learn more about probability
brainly.com/question/11234923
#SPJ4
What is the speed of a wave with a frequency of 2 Hz and a wavelength of 87 m

Answers
Answer:
174 m/s
Step-by-step explanation:
Formula: velocity = frequency x wavelength
V = 2 x 87
V = 174
Hope that helps!
Answer:
174
Step-by-step explanation:
Did the test
Use the numbers to place the companies in order of greatest comparative advantage to least comparative advantage in
producing large tubes of toothpaste.
O 2.1.3.4
O 4.1,2,3
O 4,3,1,2
Answers
The companies in order of greatest comparative advantage to least comparative advantage in producing large tubes of toothpaste is 4, 3, 1, 2 that is option C.
Use the numbers to place the companies in order of greatest comparative advantage to least comparative advantage in producing large tubes of toothpaste.
Toothpaste company
Large tubes
Small tubes
1) Sparkling
100 per hour
200 per hour
2) Bright White
100 per hour
250 per hour
3) Fresh!
200 per hour
250 per hour
4) Mint
150 per hour
150 per hour
Formula for comparative advantage is
CA=rate of producing large tubes/rate of producing small tube
For 1 Sparkling:
CA = 100/200
CA = 0.5
For 2 Bright White:
CA = 100/250
CA = 0.5
For 3 Fresh:
CA = 200/250
CA = 0.8
For 4 Mint:
CA = 150/150
CA = 1
thus, to place the companies in order of greatest comparative advantage to least comparative advantage in producing large tubes of toothpaste is 4, 3, 1, 2.
Learn more about Companies:
https://brainly.com/question/28889657
#SPJ4
Complete question:
Use the numbers to place the companies in order of greatest comparative advantage to least comparative advantage in
producing large tubes of toothpaste.
2.1.3.4
4.1,2,3
4,3,1,2
Save and Exit
Next
Submit
Mark this and retum
what is the slope and y-intercept for the line y = -2x
Answers
Answer:
slope = - 2, y- intercept = 0
Step-by-step explanation:
The equation of a line in slope- intercept form is
y = mx + c ( m is the slope and c the y- intercept )
y = - 2x , that is
y = - 2x + 0 ← is in slope- intercept form
with slope m = - 2 and y- intercept c = 0 ( that is the origin )
Which statement is true?
4-8 < 3
55-6
-12 >-6
Answers
Answer:
the first i believe but the one with 50 confuses me
Step-by-step explanation:
Let a,b, and c be real numbers such that 4a+2b+c=0 and ab>0. Then the equation ax 2 +bx+c=0 has
Answers
Since ab > 0, it is clear that the discriminant D > 0. Therefore, the equation ax^2 + bx + c = 0 has two distinct real roots.
Since 4a + 2b + c = 0, we can rewrite c as c = -4a - 2b. Substituting this into the quadratic equation ax^2 + bx + c = 0 gives ax^2 + bx - 4a - 2b = 0. Factoring out an 'a' gives a(x^2 + (b/a)x - 4) - 2b = 0.
Since ab > 0, we know that a and b must have the same sign. This means that either both a and b are positive or both a and b are negative. In either case, (b/a) is negative. So we can rewrite the equation as a(x^2 - |(b/a)|x - 4) - 2b = 0.
To solve for the roots of the equation, we can use the quadratic formula: x = (-b ± √(b^2 - 4ac)) / 2a. Plugging in the coefficients, we get x = (-b ± √(b^2 - 4a(-4a-2b))) / 2a, which simplifies to x = (-b ± √(b^2 + 16ab)) / 2a.
Since ab > 0, we know that b^2 + 16ab > 0. Therefore, the quadratic equation ax^2 + bx + c = 0 has two real roots.
Based on the information provided, let's consider the equation ax^2 + bx + c = 0, where a, b, and c are real numbers and 4a + 2b + c = 0. Since ab > 0, both a and b have the same sign (either both positive or both negative).
The given equation can be rewritten as a quadratic equation in the standard form:
ax^2 + bx + c = 0
Using the discriminant formula, D = b^2 - 4ac, we can analyze the nature of the roots of the quadratic equation. Given that 4a + 2b + c = 0, we can express c as:
c = -4a - 2b
Now, let's plug this value of c into the discriminant formula:
D = b^2 - 4a(-4a - 2b)
D = b^2 + 16a^2 + 8ab
Since ab > 0, it is clear that the discriminant D > 0. Therefore, the equation ax^2 + bx + c = 0 has two distinct real roots.
Visit here to learn more about quadratic equation : https://brainly.com/question/30098550
#SPJ11
PLEASE HELP!!!! 20 POINTS

Answers
Answer:
relative
Step-by-step explanation:
Two step equation help me pls step by step
The questions 36 and 37

Answers
Answer:
Step-by-step explanation:

SOLVING
================================================================
Question 36
6=-2(7-c)
Use distribution to multiply -2 by parenthesis
6=-14+2c
Add to both sides 14
20=2c
Divide 2 into both sides
10=c
Question 375(h-4)=8
Use distribution to multiply 5 by the parenthesis
5h-20=8
Add to both sides 20
5h=28
Divide 5 into both sides
\(h=\frac{28}{5}\)
Learn more;work harder
#Carryonlearning
==============================================================
Hello im in 8th grade and I need to get my grades up so anyone know the answer to
-12 minus 12x = 36
work also needs to be shown if possible thank you
Answers
Answer:
x = 3
Step-by-step explanation:
12x = 36
simply 12 will go to the other side and switches to the opposite sign for example + will be -
× will br ÷
so 36 ÷ 12 =3
x = 3