The function d =
45t gives the distance d Juan traveled in miles after t hours.
is this discrete or continuous data?
Answers
Answer:
Continuous data
Step-by-step explanation:
Given
\(d = 45t\)
Required
Discrete or Continuous?
From the question, we understand that t represents time in hours. This is a continuous data.
When multiplied by 45 to give distance, the resulting data is also continuous.
Hence, \(d = 45t\) is continuous
Answer:
d = 2.5t, continuous
Step-by-step explanation:
Just did it on Edge and got it right
Related Questions
please help!! Choose the system of equations that matches the following graph:

Answers
Answer:
tge answer is
A. x-4y=-4
3x+4y=36
Use the function g(x)=11 to find the following values g(-3), g(5), g(a), g(a+h)
Answers
The evaluated function values are g(-3) = 11, g(5) = 11, g(a) = 11 and g(a+h) = 11
Evaluating the function valuesA composite function is a function that results from combining two or more functions. It is created by using the output of one function as the input of another function.
The function g(x) is defined as g(x) = 11, which means that the output of the function is always 11, no matter what value of x is inputted.
i.e. the function g(x) = 11 always returns the value 11, regardless of the input.
Therefore, we have:
g(-3) = 11
g(5) = 11
g(a) = 11
g(a+h) = 11
So, regardless of the value of a or h, the function g(x) will always return 11.
Read more about function at
https://brainly.com/question/28532394
#SPJ1
pls help me solve this

Answers
The results of operations between vectors are, respectively:
Case A: u + w = <- 3, - 1>
Case B: - 6 · v = <6, 6>
Case C: 3 · v - 6 · w = <- 21, - 15>
Case D: 4 · w + 3 · v - 5 · u = <39, 4>
Case E: |w - v| = √(4² + 3²) = 5
How to determine the operations between vectors
In this problem we must determine the operations between vectors, this can be done by following definitions:
Vector addition
v + u = (x, y) + (x', y') = (x + x', y + y')
Scalar multiplication
α · v = α · (x, y) = (α · x, α · y)
Norm of a vector
|u| = √(x² + y²)
Now we proceed to determine the result of each operation:
Case A:
u + w = <- 6, - 3> + <3, 2>
u + w = <- 3, - 1>
Case B:
- 6 · v = - 6 · <- 1, - 1>
- 6 · v = <6, 6>
Case C:
3 · v - 6 · w = 3 · <- 1, - 1> - 6 · <3, 2>
3 · v - 6 · w = <- 3, - 3> + <- 18, - 12>
3 · v - 6 · w = <- 21, - 15>
Case D:
4 · w + 3 · v - 5 · u = 4 · <3, - 2> + 3 · <- 1, - 1> - 5 · <- 6, - 3>
4 · w + 3 · v - 5 · u = <12, - 8> + <- 3, - 3> + <30, 15>
4 · w + 3 · v - 5 · u = <39, 4>
Case E:
|w - v| = |<3, 2> - <- 1, - 1>|
|w - v| = |<4, 3>|
|w - v| = √(4² + 3²) = 5
To learn more on vectors: https://brainly.com/question/31900604
#SPJ1
7 yards and 2feet equals how many feet?
Answers
Answer:
23 ft
Step-by-step explanation:
a yard is 3 feet multiply it by 7 and you get 21 add 2 and you get 23. 23ft is your answer
Can u please help me with 3&4 I’m giving 20 point please help me

Answers
Answer:
Step-by-step explanation:

Find the equation of line that passes through the points (-2,2) and (10,4)
Answers
Answer:
y=1/6x-3-2
Step-by-step explanation:
rises 2 runs 12
equals rise 1 run 6
1/6x
10, 6 -2 from x =10, 4
-2a-6a-9=-9-6a-2a
help please g
Answers
Answer:
the solution to the equation -2a - 6a - 9 = -9 - 6a - 2a is all real numbers, or (-∞, +∞).
Step-by-step explanation:
To solve this equation for "a", you need to simplify and rearrange the terms so that all the "a" terms are on one side of the equation and all the constant terms are on the other side. Here are the steps:
Start by combining the "a" terms on the left side of the equation: -2a - 6a = -8a. The equation now becomes: -8a - 9 = -9 - 6a - 2a.
Combine the constant terms on the right side of the equation: -9 - 2a - 6a = -9 - 8a. The equation now becomes: -8a - 9 = -9 - 8a.
Notice that the "a" terms cancel out on both sides of the equation. This means that the equation is true for any value of "a". Therefore, the solution is all real numbers, or in interval notation: (-∞, +∞).
In summary, the solution to the equation -2a - 6a - 9 = -9 - 6a - 2a is all real numbers, or (-∞, +∞).
What is the volume of the triangular prism?
please help!! quickly its a test a look at the picture
7th grade math
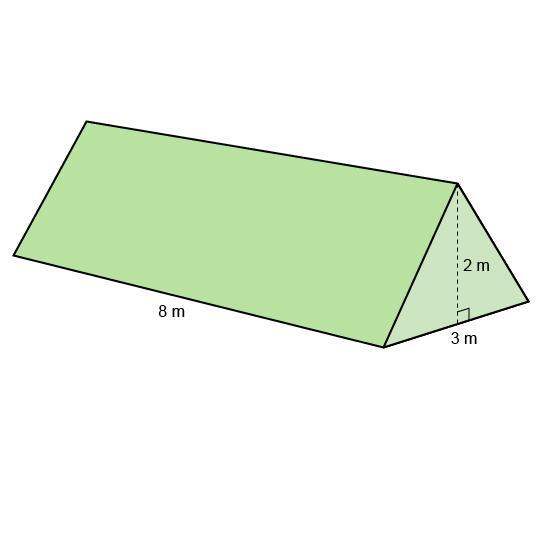
Answers
The area of the triangle is:
A = (base•height) : 2 = (3•2) : 2 = 3 m2
So the volume is:
V = 3 • 8 = 24 m3
Which expression is equivalent to StartRoot 8 x Superscript 7 Baseline y Superscript 8 Baseline EndRoot? Assume x greater-than-or-equal-to 0.
x y squared StartRoot 8 x cubed EndRoot
2 x cubed y cubed StartRoot x y squared EndRoot
2 x cubed y Superscript 4 Baseline StartRoot 2 x EndRoot
4 x cubed y Superscript 4 Baseline StartRoot x EndRoot
Answers
The expression that is equivalent to StartRoot \(8 x^7 y^8\) EndRoot is (\(2 x^3 y^4\) StartRoot 2 x EndRoot)^2.
To understand why this is the case, let's break down each expression and simplify them step by step:
StartRoot \(8 x^7 y^8\) EndRoot:
We can rewrite 8 as \(2^3\), and since the square root can be split over multiplication, we have StartRoot \((2^3) x^7 y^8\) EndRoot. Applying the exponent rule for square roots, we get StartRoot \(2^3\) EndRoot StartRoot \(x^7\) EndRoot StartRoot \(y^8\) EndRoot.
Simplifying further, we have 2 StartRoot \(2 x^3 y^4\) EndRoot StartRoot \(2^2\) EndRoot StartRoot \(x^2\) EndRoot StartRoot \(y^4\) EndRoot. Finally, we obtain 2 \(x^3 y^4\) StartRoot 2 x EndRoot, which is the expression in question.
(\(2 x y^2\) StartRoot 8 x^3 EndRoot)^2:
Expanding the expression inside the parentheses, we have \(2 x y^2\)StartRoot \((2^3) x^3\) EndRoot. Applying the exponent rule for square roots, we get \(2 x y^2\) StartRoot \(2^3\) EndRoot StartRoot \(x^3\) EndRoot.
Simplifying further, we have \(2 x y^2\) StartRoot 2 x EndRoot. Squaring the entire expression, we obtain (\(2 x y^2\) StartRoot 2 x EndRoot)^2.
Therefore, the expression (\(2 x^3 y^4\) StartRoot 2 x EndRoot)^2 is equivalent to StartRoot \(8 x^7 y^8\) EndRoot.
For more such questions on expression
https://brainly.com/question/1859113
#SPJ8
6.258 rounded to the nearest hundredth
Answers
Answer:
6.26
Step-by-step explanation:
Integer Part: 6
Fractional Part: 258
If the last digit in the fractional part of 6.258 is less than 5, then simply remove the last the digit of the fractional part.
If the last digit in the fractional part of 6.258 is 5 or more and the second digit in the fractional part is less than 9, then add 1 to the second digit of the fractional part and remove the third digit.
If the last digit in the fractional part of 6.258 is 5 or more and the second digit in the fractional part is 9, and the first digit in the fractional part is less than 9, then add 1 to the first digit in fractional part and make the second digit in fractional part 0. Then remove the third digit.
If the last digit in the fractional part of 6.258 is 5 or more and the second digit in the fractional part is 9, and the first digit in the fractional part is 9, then add 1 to the integer part and make the fractional part 00.
With 6.258, rule B applies and 6.258 rounded to the nearest hundredth is 2.26
The Boston Celtics have won 16 NBA championships over approximately 50 years. Thus is may seemreasonable to to assume that in a given year the Celtics win the title with probability p = 16=50 = 0:32,independent of any other year. Given such a model, what would be the probability of the Celtics winningeight straight championships
Answers
Answer:
0.0001 = 0.01% probability of the Celtics winning eight straight championships.
Step-by-step explanation:
For each year, there are only two possible outcomes. Either the Celtics are the champions, or they are not. Each year is independent of other years. So we use the binomial probability distribution to solve this question.
Binomial probability distribution
The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.
\(P(X = x) = C_{n,x}.p^{x}.(1-p)^{n-x}\)
In which \(C_{n,x}\) is the number of different combinations of x objects from a set of n elements, given by the following formula.
\(C_{n,x} = \frac{n!}{x!(n-x)!}\)
And p is the probability of X happening.
What would be the probability of the Celtics winning eight straight championships?
Each year, we have that \(p = 0.32\)
Eight straight championships: \(P(X = 8)\) when n = 8. So
\(P(X = x) = C_{n,x}.p^{x}.(1-p)^{n-x}\)
\(P(X = 8) = C_{8,8}.(0.32)^{8}.(0.68)^{0} = 0.0001\)
0.0001 = 0.01% probability of the Celtics winning eight straight championships.
Calculate each compound event probability: a. X ≤ 15, n = 20, π = .70 (Round your answer to 4 decimal places.) b. X > 8, n = 11, π = .65 (Round your answer to 4 decimal places.) c. X ≤ 1, n = 13, π = .40 (Round your answer to 4 decimal places.)
Answers
For X ≤ 15, n = 20, π = .70 ; compound event probability is approximately 0.0008 .
For X > 8, n = 11, π = .65 ; compound event probability is approximately 0.9198.
For X ≤ 1, n = 13, π = .40 ; compound event probability is approximately 0.6646 .
a. To calculate the probability of the event X ≤ 15, n = 20, π = .70, we will use the binomial distribution formula:
P(X ≤ 15)
= ∑_(k=0)¹⁵〖(20Ck)(0.70)^k (0.30)^(20-k) 〗
Using a binomial distribution calculator, we can find this probability to be approximately 0.0008 (rounded to 4 decimal places).
b. To calculate the probability of the event X > 8, n = 11, π = .65, we will first find the probability of X ≤ 8, and then subtract this value from 1 to find the complement probability:
P(X > 8) = 1 - P(X ≤ 8)
= 1 - ∑_(k=0)⁸〖(11Ck)(0.65)^k (0.35)^(11-k)〗
Using a binomial distribution calculator, we can find the probability of X ≤ 8 to be approximately 0.0802.
Therefore, the probability of X > 8 is approximately 0.9198 (rounded to 4 decimal places).
c. To calculate the probability of the event X ≤ 1, n = 13, π = .40, we will use the binomial distribution formula:
P(X ≤ 1)
= ∑_(k=0)¹〖(13Ck)(0.40)^k (0.60)^(13-k)〗
Using a binomial distribution calculator, we can find this probability to be approximately 0.6646 (rounded to 4 decimal places).
For more such questions on event probability visit:
https://brainly.com/question/30390037
#SPJ8
find the area of a rectangle with a length of 10 inches and a width of 4 inches
Answers
Answer:
40 in²---------------------
Formula for area of a rectangle with dimensions l and w is:
A = lwSubstitute 10 for l and 4 for w:
A = 10*4A = 40 in²A space shuttle 275 miles above the earth is orbiting the earth once every 4 hours. How far does the shuttle travel in 1 hour? (Assume the radius of the earth is 4,000 miles.) Answer exactly or round to the nearest mile
Answers
The space shuttle travels about 6713 miles per hour. Rounded to the nearest mile, this is approximately 6713 miles per hour.
What is a radius ?
In mathematics, the radius is a term used to describe the distance from the center of a circle or a sphere to any point on its surface. It is denoted by the letter "r".
The orbit of the space shuttle is circular, so the distance it travels in one orbit is equal to the circumference of the circle with a radius of 275 + 4000 = 4275 miles (275 miles above the Earth's 4000 mile radius).
The circumference of a circle is given by the formula C = 2πr, where r is the radius of the circle and π is the mathematical constant pi (approximately 3.14). Therefore, the distance traveled by the shuttle in one orbit is:
C = 2π(4275) ≈ 26851 miles
Since the shuttle orbits once every 4 hours, its average speed is:
distance/time = 26851/4 ≈ 6713 miles per hour
Therefore, the space shuttle travels about 6713 miles per hour. Rounded to the nearest mile, this is approximately 6713 miles per hour.
To learn more about Radius from given link.
https://brainly.com/question/13449316
#SPJ1
Please help me, due tomorrow!

Answers
Answer:
x=12
Step-by-step explanation:
3x-4=2x+8
-2 +4 -2 +4
x =12
Evalute 5x + 4y; if x = 3 and y = 2
O 54
O 22
ОО
95
23
Answers
The answer is 23 becuase 15+8=23
23
Explanation:
5(3)+4(2)
15+8
you have to plug in the numbers to the given variable. like how x is 3 and y is 2 if that makes sense im not good at explaining math
Find all solutions of each equation on the interval 0≤ x <2pie
tan² x sec² x +2 sec²x - tan²x =2
Answers
The trigonometric equations has the following solutions: x = 0 + j · π or x = 0.352π + j · π or x = - 0.352π + j · π, where j is a non-negative whole number.
How to solve a trigonometric equation
In this problem we find the case of a trigonometric equation, whose solutions on the interval [0, 2π] must be found. This can be done by both algebra properties and trigonometric formulae. First, write the entire expression:
tan² x · sec² x + 2 · sec² x - tan² x = 2
Second, use trigonometric formulas to reduce the number of trigonometric functions:
tan² x · (tan² x + 1) + 2 · (tan² x + 1) - tan² x = 2
Third, expand the equation:
tan⁴ x + tan² x + 2 · tan² x + 2 - tan² x = 2
tan⁴ x + 2 · tan² x = 0
Fourth, factor the expression:
tan² x · (tan² x - 2) = 0
tan² x = 0 or tan² x = 2
tan x = 0 or tan x = ± √2
Fifth, determine the solutions to trigonometric equation:
x = 0 + j · π or x = 0.352π + j · π or x = - 0.352π + j · π, where j is a non-negative whole number.
To learn more on trigonometric equations: https://brainly.com/question/22624805
#SPJ1
3. days B) 5 days C) 4 days A can do a certain work in 15 days and B can do same work in 18 days. They work together but A had left the work after some days, and B finished the remaining work in 7 days. After how many days A had left the work?
Answers
A left the work after 3 days was solved by using work formula.
What is algebraic equation?An algebraic equation is a mathematical statement that asserts that two expressions are equal. These expressions can contain variables, which are represented by letters, and the equation states that the values of the expressions are equal for some particular values of the variables.
What is work formula?The work formula is a mathematical concept used to determine how long it will take two or more workers to complete a job together. The formula is based on the idea that the amount of work done is directly proportional to the time spent working.
In the given question,
Let's assume that A worked for x days, and therefore he left the work unfinished for (15 - x) days. During this time, B finished the remaining work in 7 days.
According to the work formula, the amount of work done by A and B together in one day is:
1/15 + 1/18 = 11/90
This means that in one day, they can complete 11/90th of the work together.
During the x days when A worked, the amount of work he did is:
x * (11/90)
And during the remaining (15 - x) days, the amount of work left undone is:
(15 - x) * (11/90)
When A left, B completed the remaining work in 7 days, so we can set up an equation:
(11/90) * 7 = (15 - x) * (11/90)
Simplifying and solving for x, we get:
x = 3
Therefore, A left the work after 3 days.
To know more about algebraic equations, visit:
https://brainly.com/question/28870584
#SPJ1
PLS HELP TIMED HW WILL GIVE BRAINLEIST

Answers
Answer:
4.8
Step-by-step explanation:
\( V_{sphere} = \frac{4}{3} \pi r^3 \)
\( 144\pi= \frac{4}{3} \pi r^3 \)
\(r^3 = \frac {3 \times 144\pi}{4\pi}\)
\(r^3 = 3 \times 36\)
\(r^3 = 108\)
\(r = \sqrt[3]{108} \\ \\ r = 4.7622031559 \\ \\ r \approx \: 4.8 \: \)
I lost my tutor and I need help on this

Answers
Question: Find the value of t in the given equation h = 2 + 9t - 5t^2 given the height of the ball is 3m.
Solution:
*
Simplify the expression 20+6k-14+k WILL MARK BRAINLIEST
Answers
6+7k
It simplifies to 6+7k
Answer:
7k + 6
Steps:
Subtract the numbers 20+6k-14k+k
6+6k+k
Combine the terms:
6+6k+k
6+7k
Rearange terms:
6+7k
7k+6
SOMEONE HELP ASAP please
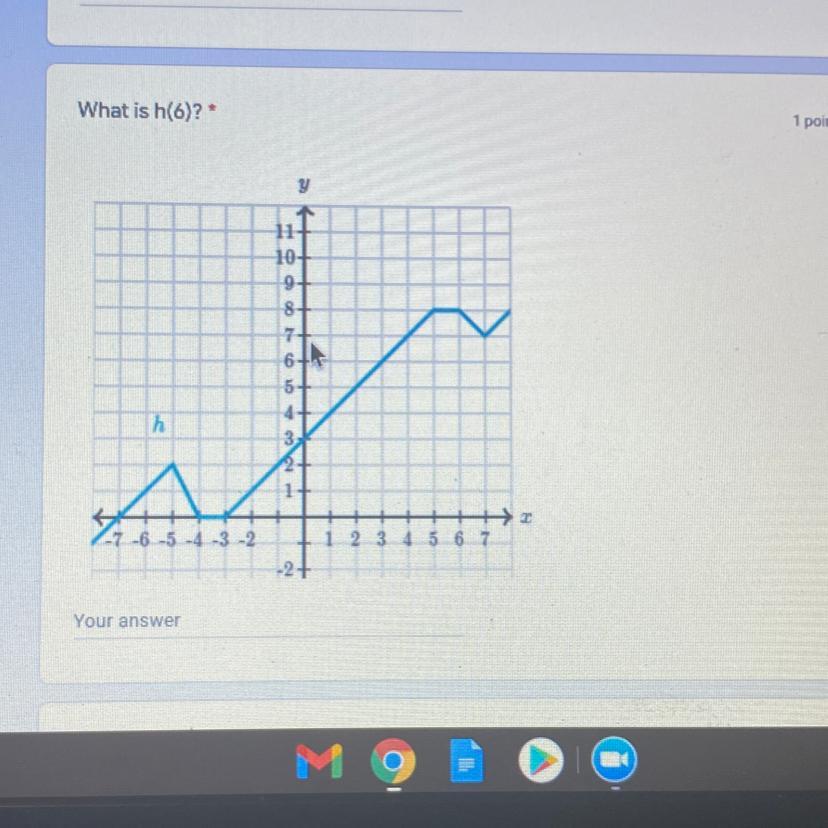
Answers
Answer:
8
Step-by-step explanation:
Look at the graph and notice when h hits 6, y turns out to be 8
Answer:4
Step-by-step explanation:
plwjahajsjwjjee helppppp!!

Answers
Answer:
30% of total students chose snowboarding as their favorite sport.
Step-by-step explanation:
We know that;
=> Total people = 500
=> Snowboarding people = 105
=> Percentage = unknown, so we can say it as x
So we can set up the equation;
x% · 500 = 105
\(\frac{x}{100}\) · 500 = 105
x · 5 = 105
x = 105/5
x = 30
So 30% of total students chose snowboarding as their favorite sport.
Hope this helps!
help please with this assignment

Answers
Answer:
13
Step-by-step explanation:
Cuz the factor of y is angle to the 115° is to the Y value
0+4=?
Help will be needed here
Answers
Answer:
40
you add a 0 to the four and boom
If you are really asking, then the answer is still 4
Answer:
4 is the correct answer
hope it is helpful to you
Last year, Lisa had $30,000 to invest. She invested some of it in an account that paid 10% simple interest per year, and she invested the rest in an account that paid 8% simple interest per year. After one year, she received a total of $2640 in interest. How much did she invest in each account?
Answers
In general, the simple interest formula is
\(A=P(1+rt)\)Where t is given in years.
And the interest is given by
\(\begin{gathered} I=A-P=P((1+rt)-1)=P(rt) \\ \Rightarrow I=P(rt) \end{gathered}\)Let B the initial amount Lisa invested in the 10% interest account and C the amount she invested in the 8% account.
Therefore,
\(\begin{gathered} B+C=30000 \\ I_B+I_C=2640 \end{gathered}\)Expanding the second equation,
\(\begin{gathered} \Rightarrow B(10\%\cdot1)+C(8\%\cdot1)=2640 \\ \Rightarrow B(0.10)+C(0.08)=2640 \end{gathered}\)The system of equations becomes
\(\begin{gathered} B+C=30000 \\ \text{and} \\ 0.1B+0.08C=2640 \end{gathered}\)From the first equation, B=30000-C. Substitute into the second equation as shown below
\(\begin{gathered} B=30000-C \\ \Rightarrow0.1(30000-C)+0.08C=2640 \\ \Rightarrow3000-0.1C+0.08C=2640 \\ \Rightarrow C=\frac{360}{0.02}=18000 \\ \Rightarrow C=18000 \end{gathered}\)And
\(\begin{gathered} C=18000 \\ \Rightarrow B=30000-18000=12000 \\ \Rightarrow B=12000 \end{gathered}\)Therefore, she invested $12000 in the 10% account and $18000 in the 8% account.
help....................

Answers
The unit of the rate of change is (b) dollars per month
How to determine the unit of the rate of changeFrom the question, we have the following parameters that can be used in our computation:
The table of values
Where we have
y = total amount in dollars
x = number of months
The rate of change is calculated as
Rate = y/x
substitute the known values in the above equation, so, we have the following representation
Rate = total amount in dollars/number of months
So, we have
Unit = dollars per month
Read more about rate of change at
https://brainly.com/question/31965106
#SPJ1
Could someone please help me?

Answers
Answer:
Option B
Step-by-step explanation:
Use the formula
\(x = \frac{-b\±\sqrt{b^{2}-4ac } }{2a}\)
now input the values. In equation \(x^{2} - 5x + 7 = 0\), a = 1, b = -5 & c = 7
By taking positive sign we get,
\(x = \frac{-b+\sqrt{b^{2}-4ac } }{2a}\)
⇒\(x = \frac{-(-5)+\sqrt{(-5)^{2}-4.1.7 } }{2.1}\)
⇒\(x = \frac{5+\sqrt{25-28 } }{2}\)
⇒\(x = \frac{5+\sqrt{-3 } }{2}\)
In the same way, by taking minus sign, we get \(x = \frac{5-\sqrt{-3 } }{2}\)
Need help on this question pls help!!!!!!!
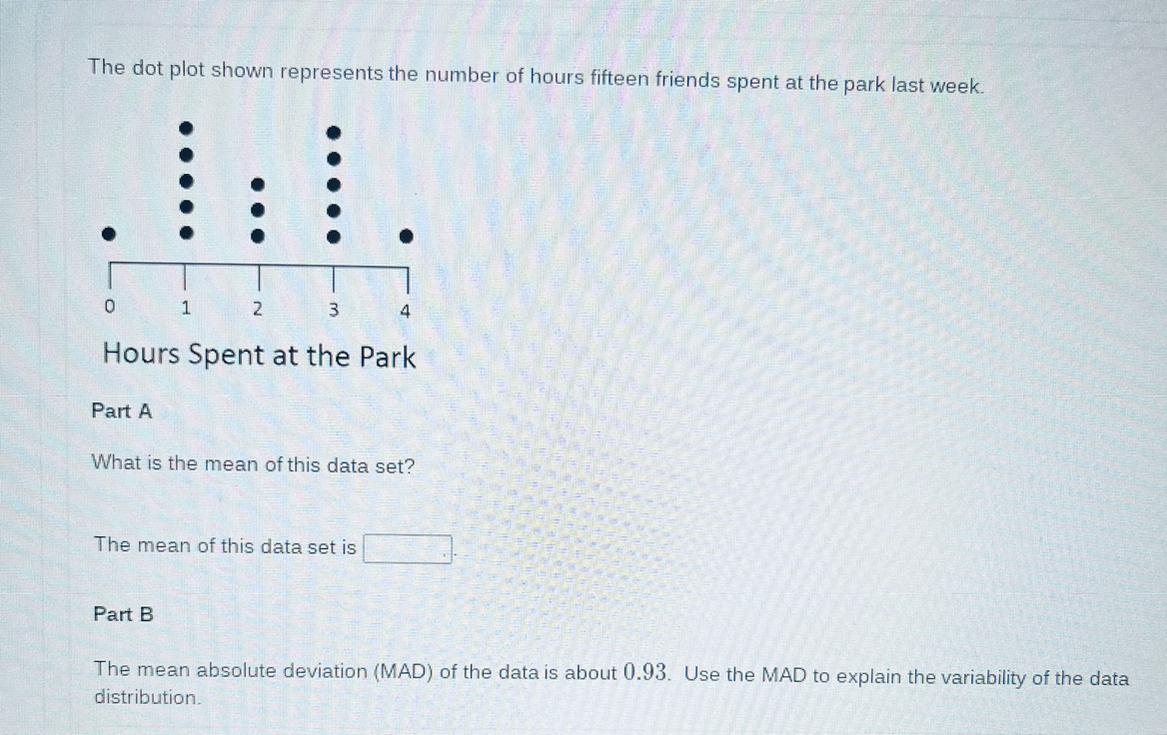
Answers
Explanation for mean:
There are 15 dots total throughout 5 lines. 15/5=3. For the mean you add up the total number of dots and divide it by the amount of categories.
find the steps to find the inverse

Answers
The inverse of f(x) = x^(7/9) using exponential notation is f(x) = x^(9/7)
what are inverse functions?An inverse function in mathematics is a function that "undoes" another function.
In other words, if f(x) yields y, then y entered into the inverse of f yields the output x.
An invertible function is one that has an inverse, and the inverse is represented by the symbol f⁻¹.
How to find the inverse functionThe given function is of the form
f(x) = x^(7/9), this is equivalent to ⁹√x⁷
say f(x) = y, then
f(x) = y = x^(7/9)
y = x^(7/9)
solving for the inverse, of y = x^(7/9)
y = x^(7/9)
y^(9/7) = x
interchanging the letters
y = x^(9/7)
hence the inverse function is solved to be f⁻¹(x) = x^(9/7)
Learn more about inverse function :
https://brainly.com/question/11735394
#SPJ1