The guidance department has reported that of the senior class 2. 3% are members of key club 8. 6% are enrolled in AP physics and 1. 9% are in both
Answers
The percentage is 9.0% of the senior class are either members of the Key Club, enrolled in AP Physics, or both.
We need to find the percentage of seniors who are either members of the Key Club, enrolled in AP Physics, or both. We can use the formula:
Total percentage = Key Club percentage + AP Physics percentage - Both percentage
Step 1: Identify the given percentages
Key Club percentage = 2.3%
AP Physics percentage = 8.6%
Both percentage = 1.9%
Step 2: Apply the formula
Total percentage = 2.3% + 8.6% - 1.9%
Step 3: Calculate the result
Total percentage = 9.0%
So, 9.0% of the senior class are either members of the Key Club, enrolled in AP Physics, or both.
Learn more about percentage,
https://brainly.com/question/24877689
#SPJ11
Related Questions
Write a conjecture that describes the pattern below.
3, 9, 27, 81...
Answers
Answer:
3 times 3 is 9
9 times 3 is 27
27 times 3 is 81
Step-by-step explanation:
how do you solve y= 2x + 3 by using a table of solutions and then graphing?
Answers
Answer:
1. Create a table that has a column for x and a column for y.
2. Plugin values for x and solve for y using the equation.
X | Y
-2 | -1
-1 | 1
0 | 3
1 | 5
2 | 7
3. Plot these values on a coordinate plane to graph them.

A person who is 2 m tall casts a shadow that is 5 m long. At the same time, a building casts a shadow that is
24 m long. How tall is the building? Please show me how u get the answer
Answers
Answer:
9.6
Step-by-step explanation:
First you figure out that the shadow is 2.5 times larger than what is casting it. Then you divide 24 by 2.5.
PLEASE HELP ASAP!!!!!!!
1) If the slope of line a is 5 and the slope of line b is -5, then what is true about lines a and b (assume lines a and b are coplanar)?
A. they are parallel
B. they are perpendicular
C. they are intersecting lines
2) If the slope of line a is 1/4 and the slope of line b is -1/4, then what is true about lines a and b (assume lines a and b are coplanar)?
A. they are parallel
B. they are perpendicular
C. they are intersecting lines
3) If the slope of line a is 3 and the slope of line b is 3, then what is true about lines a and b (assume lines a and b are coplanar)?
A. they are parallel
B. they are perpendicular
C. they are intersecting lines
Answers
On solving the provided question, we got to know that - they are perpendicular, they are perpendicular and they are intersecting lines
what are perpendicular lines?A straight line that intersects another straight line at a 90° angle is said to be perpendicular. A little square is placed in the middle of two vertical lines to represent a 90° angle, often known as a right angle, as illustrated. The two straight lines in this instance are perpendicular to one another since they connect at a right angle.
1) For this case, we have to define perpendicular lines:
\(m1 * m2 = -1\)
\(m1 = 1/5\\m2 = -5\\so, m1*m2 = -1\\\)
they are perpendicular
2) they are perpendicular
3) they are intersecting lines
To know more about perpendicular lines visit:
https://brainly.com/question/18271653
#SPJ1
1. (#1) Find the area of the figure.
8
16
16
8
24
12
12
4
4
Answers
Answer:
80
Step-by-step explanation:
8+8= 16
12+12=24
16+16=32
4+4=8
16+8=24
24+24=48
48+32=80
Explanation:
Trust me ezz
I am so confused, what do I need to do here?

Answers
The radian measure of Angle E should be labeled π/3 or 60 degrees, and F should be labeled 2(π/3) or 120 degrees.
How do we identify the radian measures of each angle?A full circle in radian measures is 2π and half π
If we divide π into 3 equal parts it should be π/3 radian.
Angle EAP would be π/3 radians because E is one-third of the way from A to P.
In degrees, π/3 radians is equal to (180/π) × π/3 = 60°
Angle FAP would be 2×(π/3) radians givn that F is 2/3 of the way from A to P.
In degrees, 2×(π/3) radians is equal to (180/π) × 2(π/3) = 120°.
Find more exercises on radian measure;
https://brainly.com/question/29163166
#SPJ1
Students arrive at the Administrative Services Office at an average of one every 12 minutes, and their requests take on average 10 minutes to be processed. The service counter is staffed by only one clerk, Judy Gumshoes, who works eight hours per day. Assume Poisson arrivals and exponential service times. Required: (a) What percentage of time is Judy idle? (Round your answer to 2 decimal places. Omit the "%" sign in your response.) (b) How much time, on average, does a student spend waiting in line? (Round your answer to the nearest whole number.) (c) How long is the (waiting) line on average? (Round your answer to 2 decimal places.) (d) What is the probability that an arriving student (just before entering the Administrative Services Office) will find at least one other student waiting in line? (Round your answer to 3 decimal places.)
Answers
The probability that an arriving student will find at least one other student waiting in line is approximately 0.167.
To solve this problem, we'll use the M/M/1 queueing model with Poisson arrivals and exponential service times. Let's calculate the required values: (a) Percentage of time Judy is idle: The utilization of the system (ρ) is the ratio of the average service time to the average interarrival time. In this case, the average service time is 10 minutes, and the average interarrival time is 12 minutes. Utilization (ρ) = Average service time / Average interarrival time = 10 / 12 = 5/6 ≈ 0.8333
The percentage of time Judy is idle is given by (1 - ρ) multiplied by 100: Idle percentage = (1 - 0.8333) * 100 ≈ 16.67%. Therefore, Judy is idle approximately 16.67% of the time. (b) Average waiting time for a student:
The average waiting time in a queue (Wq) can be calculated using Little's Law: Wq = Lq / λ, where Lq is the average number of customers in the queue and λ is the arrival rate. In this case, λ (arrival rate) = 1 customer per 12 minutes, and Lq can be calculated using the queuing formula: Lq = ρ^2 / (1 - ρ). Plugging in the values: Lq = (5/6)^2 / (1 - 5/6) = 25/6 ≈ 4.17 customers Wq = Lq / λ = 4.17 / (1/12) = 50 minutes. Therefore, on average, a student spends approximately 50 minutes waiting in line.
(c) Average length of the line: The average number of customers in the system (L) can be calculated using Little's Law: L = λ * W, where W is the average time a customer spends in the system. In this case, λ (arrival rate) = 1 customer per 12 minutes, and W can be calculated as W = Wq + 1/μ, where μ is the service rate (1/10 customers per minute). Plugging in the values: W = 50 + 1/ (1/10) = 50 + 10 = 60 minutes. L = λ * W = (1/12) * 60 = 5 customers. Therefore, on average, the line consists of approximately 5 customers.
(d) Probability of finding at least one student waiting in line: The probability that an arriving student finds at least one other student waiting in line is equal to the probability that the system is not empty. The probability that the system is not empty (P0) can be calculated using the formula: P0 = 1 - ρ, where ρ is the utilization. Plugging in the values:
P0 = 1 - 0.8333 ≈ 0.1667. Therefore, the probability that an arriving student will find at least one other student waiting in line is approximately 0.167.
To learn more about Probability, click here: brainly.com/question/16988487
#SPJ11
what is 0.00002468 to the nearest hundrad thousandth as an estimate
Answers
Answer:
0.00002
Step-by-step explanation:
The value of 0.00002468 after rounding it to the nearest hundred thousandth is 200,000.
Given,
We need to find what is 0.00002468 to the nearest hundred thousandth as an estimate.
What is the place value of a decimal number?234.56789
2 - hundreds place value
3 - tens
4 - ones
5 - tenths
6 - hundredths
7 - thousandths
8 - ten thousandths
9 - hundred thousandths
We have,
0.00002468
Here the value in hundred-thousandths is 2
2468 can be assumed as 246800.
We can round this to either 200,000 or 300,000
If it is greater than 249,000 we will round it to 300,000.
If it is less than 249,000 we will round it to 200,000.
246,800 is less than 249,000 so we will round it to 200,000.
Thus the value of 0.00002468 after rounding it to the nearest hundred thousandth is 200,000.
Learn more about rounding decimal numbers here:
https://brainly.com/question/14890644
#SPJ2
1.) Use the line drawing tool to draw the equation Y=1+1.50X Label your line 'A'. 2.) Use the line drawing tool to draw the equation Y= 18-1.25X Label your line 'B' 3.) Use the point drawing tool to indicate the point where both equations are equal. Label this point 'Equilibrium Carefully follow the instructions above, and only draw the required objects.
Answers
The line drawing tool is used to draw the equations Y=1+1.50X and Y= 18-1.25X and the intersection point is labeled.
To draw the lines and indicate the point of intersection, you can follow these steps:
1. Draw a coordinate system on a piece of paper or using a drawing software.
2. For line A, plot two points on the coordinate system using the equation Y = 1 + 1.50X. Choose any two X values and calculate the corresponding Y values using the equation.
3. Connect the two points with a straight line and label it as line A.
4. For line B, plot two points on the coordinate system using the equation Y = 18 - 1.25X. Choose any two X values and calculate the corresponding Y values using the equation.
5. Connect the two points with a straight line and label it as line B.
6. Find the point of intersection between line A and line B. This is the point where both equations are equal. You can calculate this point by solving the system of equations Y = 1 + 1.50X and Y = 18 - 1.25X simultaneously.
7. Once you find the X and Y values of the point of intersection, mark it on the coordinate system and label it as 'Equilibrium'.
To know more about equations, refer here:
brainly.com/question/31382933
#SPJ4

Classify the numbers as rational or irrational.
6
√2.6
√2+6

Answers
Step-by-step explanation:
\( \sqrt 2, \: \sqrt 2. 6 \: \& \: \sqrt 2 + 6\) are irrational and 6 is the only rational number.
a tanker is being filled with gasoline. at time , the tanker has 70 gallons of gasoline in it. using a left riemann sum, approximate the area under to the t axis for using 4 rectangles. 186.2 correct using a right riemann sum, approximate the area under to the t axis for using 4 rectangles. 202 correct using the right riemann sum, approximately what is the total amount of gallons in the tanker at 10 minutes?
Answers
The right Riemann sum approximation for the total amount of gasoline in the tanker at 10 minutes is 685 gallons.
We are given the area under the curve (AUC) of f(t) from 0 to 10 using 4 rectangles using the right Riemann sum, which is 202. Let's find out what is the total amount of gallons in the tanker at 10 minutes.
Using the right Riemann sum, the total amount of gallons in the tanker at 10 minutes can be calculated as follows:
Firstly, we need to find the width of each rectangle, which can be calculated as follows:
Δt = (b - a) / n, where a = 0, b = 10, and n = 4
Δt = (10 - 0) / 4 = 2.5
This means the width of each rectangle is 2.5 minutes.
Now, we need to find the height of each rectangle. We can do this by calculating the value of f(t) at the right endpoint of each rectangle. Here, we have 4 rectangles, and the right endpoints are 2.5, 5, 7.5, and 10.
Let's calculate the value of f(t) at each endpoint.
f(2.5) = 54
f(5) = 62
f(7.5) = 78
f(10) = 80
Next, we need to calculate the area of each rectangle using the right Riemann sum.
The area of each rectangle is given by:
Area = f(tₐ) * Δt, where tₐ is the right endpoint of the a-th rectangle.
Using the right Riemann sum, we add the area of all rectangles to get the total area under the curve. This can be calculated as follows:
Total area = Area1 + Area2 + Area3 + Area4
Total area = f(2.5) * Δt + f(5) * Δt + f(7.5) * Δt + f(10) * Δt
Total area = 54 * 2.5 + 62 * 2.5 + 78 * 2.5 + 80 * 2.5
Total area = 135 + 155 + 195 + 200
Total area = 685 gallons
This means the total amount of gallons in the tanker at 10 minutes using the right Riemann sum is 685 gallons.
To know more about the "right Riemann sum": https://brainly.com/question/29275224
#SPJ11
determine if each relationship represtents a fuctikn chose yes or no for each relationship

Answers
Answer:
Yes
no
no
yes
Step-by-step explanation:
I hope it's serving
:v
Round 1.3185 to 1 decimal place
Answers
Answer:
1
Step-by-step explanation:
Because 1.38185 is below 1.5 so it rounds to 1
WORTH 20 POINTS
Write an algebraic expression
Eight less than x, times the sum of x and four
Answers

Part II: 2nd Order Initial-Value ODE [20 points) Solve the following initial value problem using Euler's method over the interval from x= 0 to x= 0.4 using 2 integration steps. The initial conditions for this problem is y(0)= 2, and y (O)=- 4. y" + 3y' – 4y + 12e-2x = 0 Hint: Convert the 2nd order ODE into a system of 1st order ODE equations and solve them simultaneously.
Answers
Given 2nd order Initial-Value ODE as, y" + 3y' – 4y + 12e-2x = 0Convert the 2nd order ODE into a system of 1st order ODE equations as follows:Let y'=zdy/dx = dz/dxSo, y" = d²y/dx² = d/dx(dz/dx) = dz²/dx².
Again, the equation becomes, dz²/dx² + 3z – 4y + 12e^(-2x) = 0The given Initial values for the problem is:y(0) = 2y'(0) = -4Therefore, using Euler's Method, over the interval from x = 0 to x = 0.4 and using 2 integration steps,We can say that the h = 0.2 (since we are taking 2 integration steps and the interval is from 0 to 0.4, which gives 0.4/2 = 0.2)So, the Main answer is:
Given y" + 3y' – 4y + 12e-2x = 0 Initial values:y(0) = 2, y'(0) = -4We know that, y'=zdy/dx = dz/dxSo, y" = d²y/dx² = d/dx(dz/dx) = dz²/dx²Now, dz²/dx² + 3z – 4y + 12e^(-2x) = 0.
We need to solve this system of first-order differential equations by applying Euler's method to find out the value of y at x=0.2 and x=0.4.
Substituting h = 0.2 in the above equations and using Euler's Method, we getThe first step is: x = 0, y = 2, z = -4 Therefore, z1 = z0 + h (-4).
Substituting the values we get, z1 = -4 – (0.2) (3) ( -4) – (0.2) (4) ( 2 + 12 e^(-2(0)) ) = -2.12So, the value of z at x=0.2 is -2.12. Similarly, we can get the value of y at x=0.2 using Euler's method.The second step is: x = 0.2, y = 1.56, z = -2.12Therefore, z2 = z1 + h ( -2.12 ).
Substituting the values we get,z2 = -2.12 - (0.2) (3) ( -2.12) - (0.2) (4) ( 1.56 + 12 e^(-2(0.2)) ) = -1.3148So, the value of z at x=0.4 is -1.3148.Similarly, we can get the value of y at x=0.4 using Euler's method.
Hence, the required answer is, y (0.4) = 0.2281
Solve the given initial value problem using Euler's method over the interval from x = 0 to x = 0.4 using 2 integration steps.
The given initial conditions for this problem is y(0) = 2, and y'(0) = -4. The 2nd order ODE is given as y" + 3y' – 4y + 12e-2x = 0.
We need to convert this 2nd order ODE into a system of 1st order ODE equations. Let y' = z. Therefore, dy/dx = dz/dx. So, y" = d²y/dx² = d/dx(dz/dx) = dz²/dx². Substituting these values in the given equation, we get dz²/dx² + 3z – 4y + 12e^(-2x) = 0.
To solve this system of first-order differential equations, we will apply Euler's method to find out the value of y at x=0.2 and x=0.4. Substituting h = 0.2 in the above equations and using Euler's Method, we get the values of y and z at x=0.2 and x=0.4.
Therefore, the required answer is y (0.4) = 0.2281. Hence, the solution to the given problem using Euler's method is y (0.4) = 0.2281.
To know more about Euler's Method :
brainly.com/question/30699690
#SPJ11
Is the average of a sum the sum of the averages?.
Answers
The average of a sum and the sum of the averages are not same.
The average of a sum is mean of sum of data. Total sum divided by total number of sum.
Whereas , The sum of the average is sum of mean of data. Total sum of averages of data.
These two terms are not same.
For example : Assume x₁ , x₂ , x₃ , . . . , xₙ be a data
S₁ , S₂ , . . . , Sₙ be sum of data
A₁ , A₂ , . . . , Aₙ be average of data
where n is total number of sum of data
The Average of sum will be = S₁ + S₂ + . . . + Sₙ / n
The sum of average will be = A₁ + A₂ + . . . + Aₙ
Hence, The average of sum and Sum of average are different.
To know more about Average here
https://brainly.com/question/16612044
#SPJ4
beginning at sea level a scuba diver dove 1 2/3 feet into the water , and then dove an additional 3 2/5 feet at what elevation is the scuba diver
Answers
The given details are illustrations of addition and subtractions of fractions. The scuba driver is at an elevation of \(-5\frac{1}{15}\) ft below the sea level.
Given that:
\(n_1 = 1\frac 23\) --- the first dive
\(n_2 = 3\frac 25\) ---- the additional dive
From the question, we understand that the diver starts at the sea level.
This is represented with 0ft.
So, the diver's elevation (d) is calculated as follows:
\(d = 0 - n_1 - n_2\) --- we use subtraction because the diver is below the sea level
So, we have:
\(d = 0 - 1\frac 23 - 3\frac 25\)
\(d = - 1\frac 23 - 3\frac 25\)
Convert fractions
\(d = - \frac 53 - \frac{17}5\)
Take LCM
\(d = \frac{-5 \times 5 - 17 \times 3}{15}\)
\(d = \frac{-76}{15}\)
Reduce fraction
\(d = -5\frac{1}{15}\)
The above value means that the diver's elevation is at \(-5\frac{1}{15}\) ft below the sea level.
Read more about fractions at:
https://brainly.com/question/18134643
Answer:
The above value means that the diver's elevation is below sea level.
Help me please solve the following equation for x.
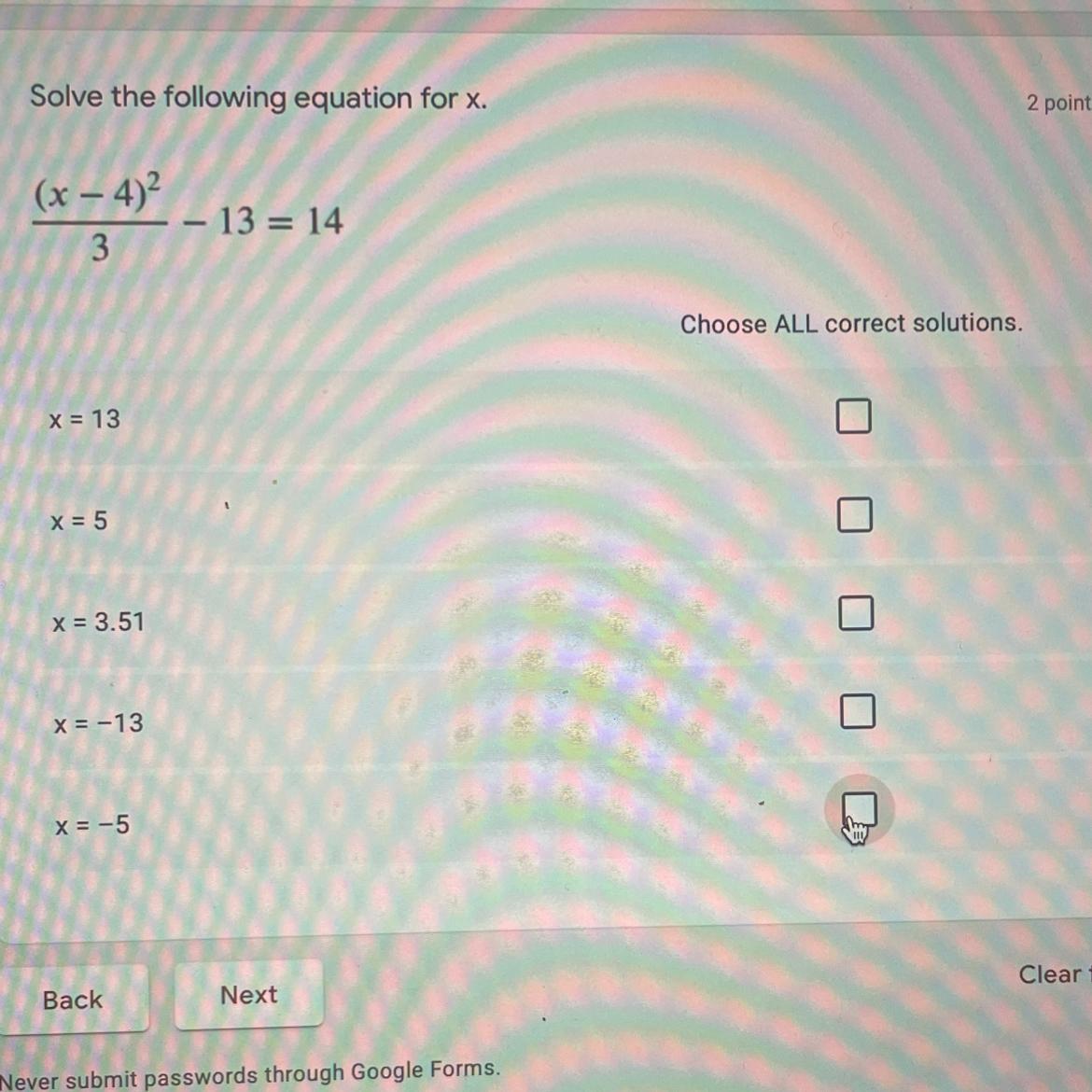
Answers
Answer:
x = 13
x = -5
Step-by-step explanation:
\(\frac{(x-4)^2}{3}-13=14\\\frac{(x-4)^2}{3}=27\\(x-4)^2=81\\x-4=\sqrt{81}\\\\ x-4=9\\x=13\\\\x-4=-9\\x=-5\)
Rewrite the equation below so that it does not have fractions.
Do not use decimals in your answer.

Answers
Answer:
x=17/14
Step-by-step explanation:
(7/9)x+2=(5/6)
18 is the least common multiple between 9 and 6, so we can multiply each fraction by 18.
7 18 126
---- * ------ = -------- = 14
9 1 9
14x+2=(5/6)
5 18 90
---- * ------ = --------- = 15
6 1 6
14x+2=15
+2 +2
14x=17
x=17/14
Hope this helps!
If f(x)=x+7 and g(x)=x²−6, find the following. a. f(g(0)) b. g(f(0)) c. f(g(x)) d. g(f(x)) e. f(f(−7)) f. g(g(4)) g. f(f(x)) h. g(g(x))
Answers
The values of the given expressions are: a. f(g(0)) = 1, b. g(f(0)) = 43, c. f(g(x)) = x² + 1, d. g(f(x)) = x² + 14x + 43, e. f(f(-7)) = 7, f. g(g(4)) = 94, g. f(f(x)) = x + 14, h. g(g(x)) = x⁴ - 12x² + 30
To find the values of the given expressions, let's substitute the functions into each other as necessary:
a. f(g(0)):
First, evaluate g(0):
g(0) = 0² - 6 = -6
Then, substitute g(0) into f(x):
f(g(0)) = f(-6) = -6 + 7 = 1
b. g(f(0)):
First, evaluate f(0):
f(0) = 0 + 7 = 7
Then, substitute f(0) into g(x):
g(f(0)) = g(7) = 7² - 6 = 49 - 6 = 43
c. f(g(x)):
Substitute g(x) into f(x):
f(g(x)) = g(x) + 7 = (x² - 6) + 7 = x² + 1
d. g(f(x)):
Substitute f(x) into g(x):
g(f(x)) = (f(x))² - 6 = (x + 7)² - 6 = x² + 14x + 49 - 6 = x² + 14x + 43
e. f(f(-7)):
Evaluate f(-7):
f(-7) = -7 + 7 = 0
Substitute f(-7) into f(x):
f(f(-7)) = f(0) = 0 + 7 = 7
f. g(g(4)):
Evaluate g(4):
g(4) = 4² - 6 = 16 - 6 = 10
Substitute g(4) into g(x):
g(g(4)) = g(10) = 10² - 6 = 100 - 6 = 94
g. f(f(x)):
Substitute f(x) into f(x):
f(f(x)) = f(x + 7) = (x + 7) + 7 = x + 14
h. g(g(x)):
Substitute g(x) into g(x):
g(g(x)) = (g(x))² - 6 = (x² - 6)² - 6 = x⁴ - 12x² + 36 - 6 = x⁴ - 12x² + 30
To learn more about function: https://brainly.com/question/25638609
#SPJ11
I need help plz I’ll appreciated

Answers
Answer:
y = x -3
Step-by-step explanation:
100 POINTS UP FOR GRABS FOR ANYONE WILLING TO HELP!!!
What are the domain and the range of this graph?
(A) The domain is {x ∈ R|x ≥ −1} and the range is {y|y ∈ R}.
(B) The domain is {x|x ∈ R} and the range is {y ∈ R|y ≥ −1}.
(C) The domain is {x ∈ R|x ≥ −1} and the range is {y ∈ R|y ≥ −1}.
(D) The domain is {x|x ∈ R} and the range is {y|y ∈ R}.

Answers
Answer:
B
Step-by-step explanation:
The domain is the span of x-values covered by the graph, while the range is the span of y-values covered by the graph.
DOMAIN:
From the graph, we can see that the span of x-values covered will be all real numbers. This is because the graph will stretch infinitely in both directions (as indicated by the arrows at the end of the graph), thereby covering all x-values.
So, the domain is all real numbers. In set notation, this is:
\(\{x|x\in \mathbb{R}\}\)
RANGE:
We can see that the span of y-values will always be greater than or equal to -1. This is because the lowest point of the graph is y=-1. The graph will never go below this point. However, it will extend infinitely upwards from this point.
So, our range is all real numbers greater than or equal to -1. In set notation, this is (and we use y because this describes the range):
\(\{y\in\mathbb{R}\ |y\geq -1}\}\)
Therefore, our answer is B.
Answer:
B
Step-by-step explanation:
I just need the answer

Answers
x + y = 1
2x - y = 4
The answer is: (5/3; -2/3)
C. The 3582600 people who quality to vote is 42%. of the total population of the country. Calculate the total population of the country
Answers
The calculated value of the total population of the country is 8530000
Calculating the total population of the country From the question, we have the following parameters that can be used in our computation:
3582600 is 42%. of the total population of the country
This means that
42%. of the total population of the country = 3582600
Express as product
So, we have
42% * the total population of the country = 3582600
Divide both sides by 42%
the total population of the country = 3582600 /42%
Evaluate
the total population of the country = 8530000
Hence, the total population of the country is 8530000
Read more about percentage at
https://brainly.com/question/24877689
#SPJ1
In a running competition, a bronze, silver and gold medal must be given to the top
three girls and top three boys. If 9 boys and 13 girls are competing, how many
different ways could the six medals possibly be given out?
Answers
Answer:
24,024 different ways
Step-by-step explanation:
There are 9 boys and 13 girls competing for the medals. The number of ways to choose 3 boys out of 9 is C(9,3) = 84. The number of ways to choose 3 girls out of 13 is C(13,3) = 286. The total number of ways to choose 6 medals is the product of these two numbers: 84 * 286 = 24024.
Can You Guys Help Me Plz

Answers
Answer:
I'm pretty sure the answer is F
Answer:
IS F
Step-by-step explanation:
I already did this work.
FMECA is a bottom-up (Hardware) or top-down (Functional) approach to risk assessment. It is inductive, or data-driven, linking elements of a failure chain as follows: Effect of Failure, Failure Mode and Causes/ Mechanisms. These elements closely resemble the modern 5 Why technique. Thus answer: To estimate reliability of software, most software prediction models use probability density function to predict, choose one Group of answer choices Mean time between failures Consensus of the team Number of failures observed in each test interval Mean time to failurel
Answers
FMECA is a bottom-up hardware approach to risk assessment. It is an inductive, or data-driven, linking elements of a failure chain as follows: Effect of Failure, Failure Mode, and Causes/Mechanisms. To estimate the reliability of software, most software prediction models use the probability density function to predict "Mean Time To Failure."
FMECA is a systematic and structured analytical methodology used to identify potential failures in a system, equipment, process, or product, and to assess the effect and probability of those failures. FMECA stands for Failure Modes, Effects, and Criticality Analysis. FMECA is similar to FMEA (Failure Modes and Effects Analysis) in that it is used to identify failure modes and assess their risk.
However, FMECA goes beyond FMEA by analyzing the criticality of each failure mode. This makes it an effective tool for identifying the most significant failure modes and prioritizing them for corrective action. A Probability Density Function (PDF) is a function that describes the likelihood of a random variable taking on a particular value.
PDF is used in software prediction models to estimate the reliability of software by predicting "Mean Time To Failure" (MTTF). MTTF is the average time between failures of a system, equipment, process, or product.
You can learn more about hardware at: brainly.com/question/32810334
#SPJ11
What is the solution to
{y=14x+3y=2x+10
Answers
Answer:
The solution is (\(\frac{7}{12}\) , \(\frac{67}{6}\))
Step-by-step explanation:
∵ y = 14x + 3 ⇒ (1)
∵ y = 2x + 10 ⇒ (2)
→ Equate equations (1) and (2) to find x
∵ 14x + 3 = 2x + 10
→ Subtract 2x from both sides
∴ 14x - 2x + 3 = 2x - 2x + 10
∴ 12x + 3 = 10
→ Subtract 3 from both sides
∴ 12x + 3 - 3 = 10 - 3
∴ 12x = 7
→ Divide both sides by 12 to find x
∵ \(\frac{12x}{12}\) \(\frac{7}{12}\)
∴ x = \(\frac{7}{12}\)
→ Substitute the value of x in equation (1) or (2) to find y
∵ y = 2(\(\frac{7}{12}\)) + 10
∴ y = \(\frac{7}{6}\) + 10
∴ y = \(\frac{67}{6}\)
∴ The solution is (\(\frac{7}{12}\) , \(\frac{67}{6}\))
On Wednesdays at Tara's Taquería four tacos are the same price as three
burritos. Last Wednesday the Lunch Bunch ordered five tacos and six
burritos, and their total bill was $8.58 (with no tax or drinks included).
Nobody in the Lunch Bunch can remember the cost of one of Tara's
tacos. Help them figure it out.
Answers
THE ANSWER IS
0.66
Or for fraction 6/10
which of the following basic functions is equivalent to the piecewise-defined function f(x)= x if x≥0 −x if x<0 ? question content area bottom part 1 a. f(x)= 1 x b. f(x)=x c. f(x)=x2 d.
Answers
The basic function equivalent to the piecewise-defined function f(x) = x if x ≥ 0 and -x if x < 0 is f(x) = |x|, which represents the absolute value of x.
The given piecewise-defined function f(x) has different expressions for different intervals. For x greater than or equal to zero, f(x) takes the value of x. For x less than zero, f(x) is equal to -x. We need to find a basic function that captures this behavior.
Among the options provided, f(x) = |x| is equivalent to the given piecewise function. The absolute value function, denoted by |x|, returns the positive value of x regardless of its sign. When x is non-negative, |x| equals x, and when x is negative, |x| is equal to -x, mirroring the conditions of the piecewise-defined function.
The function f(x) = |x| represents the absolute value of x and matches the behavior of the given piecewise-defined function, making it the equivalent basic function.
In summary, the basic function equivalent to the piecewise-defined function f(x) = x if x ≥ 0 and -x if x < 0 is f(x) = |x|, which represents the absolute value of x.
Learn more about absolute value here:
https://brainly.com/question/17360689
#SPJ11