the hawks have won 12 games this season, which is 60% of the season how many games did they play

Answer:

Let us assume number of points scored by Team B = b points.

Number of points scored by Team A 5 fewer than twice as many points as Team B, that is "5 less than 2b" = (2b-5) points .

Team C scored 80 more points than Team B, that is " 80 more than b" = (b+80) points.

Total number of points scored by all teams = 983 points.

Therefore, we can setup an equation:

(2b-5) + b + (b+80) = 983.

Therefore, an equation to represent this scenario using the variable b to represent Team B’s total points is (2b-5) + b + (b+80) = 983.

Step-by-step explanation:

Answer:

represent team b as b number of team a is five than twice as much point as team b=(2b_5)

team c scored 80 more than b that is (b+80) total number=983

so

Answer:

The zeros are x=0,3,-2

There is a multiplicity of 1 for all of them.

Step-by-step explanation:

The required value of a is 3 for the given function.

The function is defined as a mathematical expression that defines a relationship between one variable and another variable.

The function is given as follows:

f(x) = 5x²– 3

Substitute the value of x = x + a in the above function,

f(x + a) = 5(x + a)²– 3

f(x + a) = 5(x² + a² + 2ax) - 3

f(x + a) = 5x² + 5a² + 10ax - 3

f(x + a) = 5x² + 10ax + 5a² - 3    ....(i)

As per the question, we have f(x + a) = 5x²+ 30x + 42     ....(ii)

Equating the equations (i) and (ii),

So, 10a = 30

a = 30/10

a = 3

Therefore, the required value of a is 3.

Learn more about the functions here:

brainly.com/question/12431044

#SPJ2

Step-by-step explanation:

39.75 is your answer for this question

Answer: 31

Step-by-step explanation:

C = 18w + 53

611 = 18w + 53

- 53 -53

558 = 18w

divide both sides by 18.

558 / 18 = 31

Answer:

32 x 3 - 5 = 91

Step-by-step explanation:

First multiply because of order of operations (PEMDAS,) to get 96. Then subtract 5 from 96, to get 91.  

Answer:

B

Step-by-step explanation:

If we reorder the equation in a certain way then it will look like this:

y-4=1/2(x-6)

y-4=1/2x-3

y-1=1/2x

y=1/2x+1

therefore B is correct since we reduced the equation to y=1/2x+1.

It may be hard to understand but the question is basically asking which one of these answers is equal to y.

Hope this helped you and let me know if i messed up or if im correct so i can imporve from my mistakes

The size of Matthew's final payment for his student loan is approximately $32.93.

To determine the size of Matthew's final payment for his student loan, we can use the formula for the monthly payment of an amortized loan.

The formula for the monthly payment (P) of an amortized loan can be calculated using the loan amount (A), interest rate per period (r), and number of periods (n) as follows:

P = (r * A) / (1 - (1 + r)^(-n))

In this case, Matthew's student loan amount (A) is $32,500, the interest rate per period (r) is 4.80% divided by 100 to convert it to a decimal and then divided by 4 since it is compounded quarterly (r = 0.048 / 4), and the loan is amortized over 12 years, which is 12 multiplied by 12 months (n = 12 * 12 = 144).

Plugging these values into the formula, we can calculate the monthly payment (P):

P = (0.048 / 4 * 32500) / (1 - (1 + 0.048 / 4)^(-144))

Using a calculator or software, the monthly payment (P) is approximately $316.67.

Since the loan is amortized over 12 years with payments made at the end of every month, there will be a total of 144 payments. However, the final payment may be different from the regular monthly payments.

To calculate the size of the final payment, we subtract the sum of the regular monthly payments (P) for the first 143 months from the loan amount (A). The final payment will account for any remaining balance.

Final payment = Loan amount (A) - (143 * Monthly payment (P))

Final payment = $32,500 - (143 * $316.67)

Using a calculator or software, the final payment is approximately $32.93.

The size of Matthew's final payment for his student loan is approximately $32.93.

To know more about Loan, visit

brainly.com/question/26011426

#SPJ11

Answer:

See below for proof.

Step-by-step explanation:

Given logarithmic equation:

\(2\log\left(\dfrac{15}{18}\right)-\log\left(\dfrac{25}{162}\right)+\log\left(\dfrac{4}{9}\right)=\log \left(2\right)\)

We can use Log Laws to prove that the left side of the equation equals the right side of the equation.

\(\textsf{Apply the Power law:} \quad n\log_ax = \log_ax^n\)

\(\implies \log\left(\dfrac{15}{18}\right)^2-\log\left(\dfrac{25}{162}\right)+\log\left(\dfrac{4}{9}\right)\)

\(\textsf{Apply the exponent rule:} \quad \left(\dfrac{a}{b}\right)^c=\dfrac{a^c}{b^c}\)

\(\implies \log\left(\dfrac{15^2}{18^2}\right)-\log\left(\dfrac{25}{162}\right)+\log\left(\dfrac{4}{9}\right)\)

\(\implies \log\left(\dfrac{225}{324}\right)-\log\left(\dfrac{25}{162}\right)+\log\left(\dfrac{4}{9}\right)\)

\(\textsf{Apply the Quotient law:} \quad \log_ax - \log_ay=\log_a \left(\dfrac{x}{y}\right)\)

\(\implies \log\left(\dfrac{\frac{225}{324}}{\frac{25}{162}}\right)+\log\left(\dfrac{4}{9}\right)\)

\(\implies \log\left(\dfrac{225}{324}\cdot\dfrac{162}{25}\right)+\log\left(\dfrac{4}{9}\right)\)

\(\implies \log\left(\dfrac{9}{2}\right)+\log\left(\dfrac{4}{9}\right)\)

\(\textsf{Apply the Product law:}\quad \log_ax + \log_ay=\log_axy\)

\(\implies \log\left(\dfrac{9}{2} \cdot \dfrac{4}{9}\right)\)

\(\implies \log\left(\dfrac{4}{2} \right)\)

\(\implies \log \left(2\right)\)

Hence proving that the left side of the equation equals log(2).

Answer:

7r is the correct answer

Step-by-step explanation:

7 x 8 = 56

The algebraic representation that shows a dilation that is an enlargement is (5/2 x,5/2 y). (Option D)

A dilation is a type of transformation that changes the size of the shape or object.  It refers to a process of changing an object’s size by decreasing or increasing its dimensions by a scaling factor. A dilation produces an image that has the same shape as the original image but is a different size.

A dilation that results in a larger image is called an enlargement while a dilation that generates a smaller image is called a reduction. A dilation is described using the scale factor and the center of the dilation (which is a fixed point in the plane).

For a scale factor > 1, the image is an enlargement; for a scale factor < 1 and  > 0, the image is a reduction; and for a scale factor = 1, the figure and the image are congruent. Hence, for a point (x,y), algebraic representation that shows a dilation that is an enlargement is (5/2 x,5/2 y) as the scale factor is greater than 1. For the remaining options, the scale factor is between 0 and 1, hence they are reduction.

Note: The question is incomplete. The complete question probably is: Which of the following algebraic representation shows a dilation that is an enlargement? A) (1/3 x,1/3 y) B) (0.1x, 0.1y) C) (5/6 x,5/6 y) D) (5/2 x,5/2 y)

Learn more about Dilation:

https://brainly.com/question/29449871

#SPJ4

Answer:

20fish

Step-by-step explanation:

so 1/2 of 16 is 8

or 1/4 of 32 is 8

so 8+32=40

40 1/2 is 20

so 20 fish caught on Monday

Answer:

-45x + 75

Step-by-step explanation:

5(-9x + 15)         Use distributive property

= (5 * -9x) + (5 * 15)

= -45x + 75

Hope this helps!

Answer:

-45x + 75

Step-by-step explanation:

5(-9x + 15)

Distribute:

(5* -9x) + (5* 15)

-45x + 75

Answer:

I think is b

Step-by-step explanation:

Decision points

are represented in the flowchart using a diamond symbol. Answer: D. Diamond.

A

flowchart

is a kind of diagram that is used to represent an algorithm, workflow, or process. A flowchart comprises different shapes, which represent distinct steps or activities in a procedure. Flowcharts are used in different fields, such as education,

engineering

, programming, and business, to demonstrate decision making, problem-solving, process control, and project management.

Flowcharts are used to:

Visualize

processes and workflows that need to be organized or improved

Communicate a sequence of steps that are essential to complete a project

Identify the root cause of a problem

Illustrate the steps of a procedure to new employees or staff members

A decision point in a flowchart is a point where the sequence of flowchart changes its direction based on the

outcomes

of the preceding steps. Decision points are represented in the flowchart using a diamond symbol.

Learn more about

flowchart

from:

https://brainly.com/question/19130837

#SPJ11

Answer:

B.

Step-by-step explanation:

12/52=6/26=3/13

The first term on the left-hand side represents the flux of the quantity D(pu δ) across the cell boundaries, and the second term represents the change of this flux within the cell.

To integrate the 1D steady-state convection-diffusion equation over a typical cell, we can start with the given equation:

D/dx(pu δ) = d/dx (rd δ/dx)

Here, D is the diffusion coefficient, p is the velocity, r is the reaction term, u is the concentration, and δ represents the Dirac delta function.

To integrate this equation over a typical cell, we need to define the limits of the cell. Let's assume the cell extends from x_i to x_i+1, where x_i and x_i+1 are the boundaries of the cell.

Integrating the left-hand side of the equation over the cell, we have:

∫[x_i to x_i+1] D/dx(pu δ) dx = D∫[x_i to x_i+1] d(pu δ)/dx dx

Using the integration by parts technique, the integral can be written as:

= [D(pu δ)]_[x_i to x_i+1] - ∫[x_i to x_i+1] d(D(pu δ))/dx dx

Similarly, integrating the right-hand side of the equation over the cell, we have:

∫[x_i to x_i+1] d/dx (rd δ/dx) dx = [rd δ/dx]_[x_i to x_i+1]

Combining the integrals, we get:

[D(pu δ)][x_i to x_i+1] - ∫[x_i to x_i+1] d(D(pu δ))/dx dx = [rd δ/dx][x_i to x_i+1]

This equation can be further simplified and manipulated using appropriate boundary conditions and assumptions based on the specific problem at hand.

To know more about integrate refer to-

https://brainly.com/question/31744185

#SPJ11

Answer for the conveyer belt moves at 100ft/min from bales of hay to barn loft is given by :

1. Seconds taken by conveyer belt is 60 seconds.

2. Hypotenuse represents the conveyer belt in right triangle.

3. Distance is other information to calculate time.

4. 1 minute = 60 seconds.

Rate at which conveyer belts moves = 100ft/min

⇒1 minute = 100ft

⇒60seconds = 100 ft

1. Seconds taken by bale of hay to move from ground to barn loft is 60 seconds.

2. Conveyer felt represent the hypotenuse of the right triangle.

Feet represents the height , and minutes (time) represents the base.

3. Speed is given to us , to calculate time we should have distance.

4. Relation between minutes and seconds is given by:

1 minute = 60 seconds.

Therefore, for the given conveyer belt moves with 100ft/min answer of the following question are:

1. Seconds taken by moving bale of hay to barn loft is 60 seconds.

2. Conveyer belt represent hypotenuse.

3. To calculate time we need distance apart from speed.

4. One minute is equal to sixty seconds.

Learn more about moves here

brainly.com/question/14189143

#SPJ4

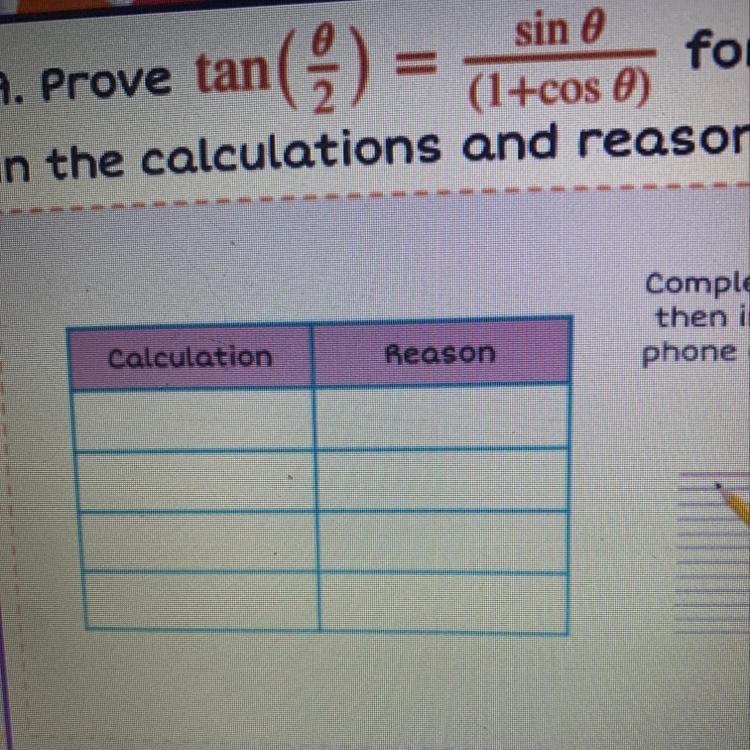
Answer:

See explanation

Step-by-step explanation:

We have to prove the identity

\(tan(\frac{\Theta }{2})=\frac{sin\Theta}{1+cos\Theta }\)

We will take right hand side of the identity

\(\frac{sin\Theta}{1+cos\Theta}=\frac{2sin(\frac{\Theta }{2})cos(\frac{\Theta }{2})}{1+[2cos^{2}(\frac{\Theta }{2})-1]}\)

\(=\frac{2sin(\frac{\Theta }{2})cos(\frac{\Theta }{2})}{2cos^{2}(\frac{\Theta }{2})}=\frac{sin(\frac{\Theta }{2})}{cos(\frac{\Theta }{2})}\)

\(=tan(\frac{\Theta }{2})\) [ Tan θ will be positive since θ lies in 1st quadrant ]

Answer:

Given that,

12-sided solid has faces numbered 1 to 12.

The table shows the results of rolling the solid 200 times

To find probability of rolling a number greater than 10.

The number of ways that the event (rolling a number greater than 10) is n(11)+n(12)

That is,

Total possible events is 200

Probability of rolling a number greater than 10 is,

Answer is :

Probability of rolling a number greater than 10 is 4/25.

The probability that the player will have an average of 0.30 or over next season is 0.664.

To answer this question, we can use the normal distribution since we know the mean and variance of the player's hits. We can assume that the distribution of hits follows a normal distribution with a mean of 0.306 and a variance of 0.10.

Let X be the number of hits the player makes next season. Then, X follows a normal distribution with a mean of 0.306 and a variance of 0.10.

To find the probability that the player will have an average of 0.30 or over next season, we need to find P(X ≥ 0.30).

We can standardize the distribution by calculating the z-score

z = (0.30 - 0.306) / sqrt(0.10) = -0.424

Using a standard normal distribution table or calculator, we can find the probability that a standard normal variable is greater than or equal to -0.424, which is 0.664.

Learn more about probability here

brainly.com/question/11234923

#SPJ4

Using a proportional relationship, it is found that:

a. The function is d = 21g.

b. Values less than 0 and greater than 20 are excluded from the domain.

c. The greatest distance that Armando can travel on the highway after the low fuel light comes on is of 52.5 miles.

A proportional relationship is a function in which the output variable is given by the input variable multiplied by a constant of proportionality, that is:

y = kx

In which k is the constant of proportionality.

Armando’s vehicle averages 21 miles per gallon on the highway, hence the distance that he can travel on g gallons is given by:

d = 21g.

The domain is the set that contains all possible input values, hence:

Hence:

Values less than 0 and greater than 20 are excluded from the domain.

The low fuel light comes in when the number of gallons remaining is:

g = 1/8 x 20 = 20/8 = 2.5 gallons.

The distance that he can travel is:

d = 21g = 21 x 2.5 = 52.5 miles.

The greatest distance that Armando can travel on the highway after the low fuel light comes on is of 52.5 miles.

More can be learned about a proportional relationship at https://brainly.com/question/10424180

#SPJ1

Answer:

s = 3t + 4w

Step-by-step explanation:

2s = 6t + 8w

s = 3t + 4w

Answer:

s = 3t+4w

Step-by-step explanation:

2s = 6t+8w

s = (6t+8w) ÷ 2

(6t÷2=3t, 8w÷2=4w)

s = 3t + 4w

Answer:

18%

Step-by-step explanation:

0.12 is 12 percent.

We also have the 0.06 percent which would just be 6 percent

We need to add up those percentages to get 18 percent, for the people surveyed that cannot swim would be 18 percent.  

Our final answer is D.

Answer:

a = 12, b = 2, z = 11

Step-by-step explanation:

  (x^5yz^4)^3/(x^3yz)

= (x^15y^3z^12)/(x^3yz)

=  x^12y^2z^11

=> a = 12

=> b = 2

=> z = 11

Answer:

a=12

b=2

z=11

Step-by-step explanation:

I got it right

Answer:

1= b to the second power, 2=a to the second power, 3=b to the fourth power, 4=a to the fourth

Step-by-step explanation: your welcome

Answer: 2)b^2+a^2

Step-by-step explanation:

x and y would have to be the same value since y(sin) and x(cos) of x and y on the unit circle is the same meaning it's the same point. Thus, cos(x-y) = cos(0) = 1. b^2+a^2=cos^2(x)+sin^2(x)= 1.

The volume of the solid bounded by the given planes is 42.67 cubic units.

To find the volume of the solid bounded by the given planes, we can set up the triple integral using the bounds determined by the intersection of the planes.

The planes z = x and y = x intersect along the line x = 0. The plane x + y = 8 intersects the line x = 0 at the point (0, 8, 0). So, we need to find the bounds for x, y, and z to set up the integral.

The bounds for x can be set from 0 to 8 because x ranges from 0 to 8 along the plane x + y = 8.

The bounds for y can be set from 0 to 8 - x because y ranges from 0 to 8 - x along the plane x + y = 8.

The bounds for z can be set from 0 to x because z ranges from 0 to x along the plane z = x.

Now, we can set up the triple integral to calculate the volume:

Volume = ∭ dV

Volume = ∭ dz dy dx (over the region determined by the bounds)

Volume = ∫₀⁸ ∫₀ (8 - x) ∫₀ˣ 1 dz dy dx

Evaluating this integral will give us the volume of the solid.

If we evaluate this integral numerically, the volume of the solid bounded by the given planes is approximately 42.67 cubic units.

To learn more about volume here:

https://brainly.com/question/28058531

#SPJ4

let's firstly get the EQUATion, of the graph before we get the inequality.

so we have a quadratic with two zeros, at -6 and 8, hmmm and we also know that it passes through (-2 , 10)

\(\begin{cases} x = -6 &\implies x +6=0\\ x = 8 &\implies x -8=0\\ \end{cases} \\\\[-0.35em] ~\dotfill\\\\ \stackrel{original~polynomial}{a ( x +6 )( x -8 ) = \stackrel{0}{y}}\hspace{5em}\textit{we also know that } \begin{cases} x=-2\\ y=10 \end{cases}\)

\(a ( -2 +6 )( -2 -8 ) = 10\implies a(4)(-10)=10\implies -40a=10 \\\\\\ a=\cfrac{10}{-40}\implies a=-\cfrac{1}{4} \\\\[-0.35em] ~\dotfill\\\\ -\cfrac{1}{4}(x+6)(x-8)=y\implies -\cfrac{1}{4}(x^2-2x-48)=y \\\\\\ ~\hfill {\Large \begin{array}{llll} -\cfrac{x^2}{4}+\cfrac{x}{2}+12=y \end{array}}~\hfill\)

now, hmmm let's notice something, the line of the graph is a solid line, that means the borderline is included in the inequality, so we'll have either ⩾ or ⩽.

so hmmm we could do a true/false region check by choosing a point and shade accordingly, or we can just settle with that, since the bottom is shaded, we're looking at "less than or equal" type, or namely ⩽, so that's our inequality

\({\Large \begin{array}{llll} -\cfrac{x^2}{4}+\cfrac{x}{2}+12\geqslant y \end{array}}\)

Answer:

$21.04

Step-by-step explanation:

Steps to take to derive the answer

Price after increase increase (100% + increase in price) x purchase price of the jeans

(100% + 65%) x 15

165% x 15

1.65 x $15 = $24.75

Price after the decrease in price = (100% - percentage decrease in price) x price after the 65% increase in price

(100% - 15%) x $24.75

85% x $24.75

0.85 x $24.75 = $21.04