the least common multiple of two whole numbers is 40. the ratio of the greater number to the lesser number is 5:4. what are the two numbers?
Answers
In a case whereby least common multiple of two whole numbers is 40. the ratio of the greater number to the lesser number is 5:4. the two numbers are 10 and 8.
How can this be calculated?Given as :
The least common multiple of two numbers = LCM = 40
The ratio of the greater number to lesser number = 5 : 4
let the greater number = 5 x
And The smaller number = 4x
∵ The LCM of numbers = 40
So, 5 × 4 × x = 40
Or, 20 × x = 60
x= 3
Then greater number = 5 x = 5 × 2 = 10
And The smaller number = 4 x = 4 × 2 = 8
Hence The two numbers are 10 and 8
Learn more about least common multiple at:
https://brainly.com/question/14052141
#SPJ1
Related Questions
Solve x2 - 13x + 30 = 0
Answers
Answer:
or, x2-(2-15)x +30= 0
or, x2-2x-15x + 30= 0
or,x(x-2)-15(x-2)=0
or, (x-2) (x-15)=0
either, or,
x-2=0 x-15=0
Answer:
x2-(10+3)x+30=0
x2-10x-3x+30=0
x(x-10)-3(x-10)=0
(x-10)(x-3)=0
either, or,
x-10=0 x-3=0
x=10 x=3
therefore,x=10,3
Determine i(t) in the given circuit by means of the Laplace transform, where A = 10. iſt) 112 Au(t) V 1F 1H The value of i(t) = AeBt C(Dt)u(t) A where A = , B = 1, C = (Click to select) A , and D =
Answers
We obtain the expression for i(t) as i(t) = \(10\)\(e^{(-t/2)}\) [(5/3)sin(√3t/2) + (5/3)cos(√3t/2)] and A = 10, B = 1, C = 5/3, and D = 1/2.
What is the Laplace transform of i(t) in the given circuit? Find the values of A, B, C, and D.To find i(t) using Laplace transform, we first need to find the Laplace transform of the given circuit elements.
The Laplace transform of the voltage source is:
L{10u(t)} = 10/s
The Laplace transform of the inductor is:
L{L(di/dt)} = sL(I(s)) - L(i(0))
Since the initial current is zero, L(i(0)) = 0. Therefore:
L{L(di/dt)} = sLI(s)
The Laplace transform of the resistor is:
L{Ri} = R * I(s)
The Laplace transform of the capacitor is:
L{(1/C)∫i dt} = I(s)/(sC)
Using Kirchhoff's voltage law, we can write:
10 = L(di/dt) + Ri + (1/C)∫i dt
Substituting the Laplace transforms, we get:
10/s = sLI(s) + RI(s) + (1/C)(I(s)/s)
Solving for I(s), we get:
I(s) = 10/(\(s^{2L}\) + Rs + 1/CS)
Substituting the given values, we get:
I(s) = 10/(s² * 1H + 1Ωs + 1/1F)I(s) = 10/(s² + s + 1)Using partial fraction decomposition, we can write:
I(s) = A/(s + 1/2 - i√3/2) + B/(s + 1/2 + i√3/2)
where A and B are constants. Solving for A and B, we get:
A = 5 + 5i√3/3B = 5 - 5i√3/3Therefore, we can write:
I(s) = (5 + 5i√3/3)/(s + 1/2 - i√3/2) + (5 - 5i√3/3)/(s + 1/2 + i√3/2)
Taking the inverse Laplace transform, we get:
i(t) =\(10\)\(e^{(-t/2)}\) [(5/3)sin(√3t/2) + (5/3)cos(√3t/2)]
Therefore, A = 10, B = 1, C = 5/3, and D = 1/2.
Learn more about Kirchhoff's voltage law
brainly.com/question/30860864
#SPJ11
0.75(8+e)=2−1.25e slove for E
Answers
The value of 'E' in the algebraic equation is -2
What is algebraic equation?Algebraic equation is a mathematical statement in which two expressions are set equal to each other.
Therefore, let solve for 'E' in the equation 0.75(8+e)=2−1.25e
Use 0.75 to open the bracket
6 + 0.75e = 2 -1.25e
Collect the like terms
0.75e+1.25e = 2-6
2e = -4
Divide both sides by 2
2e/ 2 = -4/2
e =-2
Therefore, the value of 'E' in the equation is -2
Learn more about algebraic equation here; https://brainly.com/question/2164351
#SPJ1
Using the accompanying table of data, blood platelet counts of women have a bell-shaped distribution with a mean of 255.1 and a standard deviation of 65.3. (All units are 1000 cells/uL. ) Using Chebyshev's theorem, what is known about the percentage of women with platelet counts that are within 2 standard deviations of the mean? What are the minimum and maximum possible platelet counts that are within 2 standard deviations of the mean?
Answers
Using Chebyshev's Theorem, it is found that:
At least 75% of women have platelet counts that are within 2 standard deviations of the mean.The minimum possible platelet count within 2 standard deviations of the mean is of 124.5 cells/uL and the maximum is of 385.7 cells/uL.What does Chebyshev’s Theorem state?When the distribution is unknown, Chebyshev's Theorem is used. It states that:
At least 75% of the measures are within 2 standard deviations of the mean.At least 89% of the measures are within 3 standard deviations of the mean.An in general terms, the percentage of measures within k standard deviations of the mean is given by \(100\left(1 - \frac{1}{k^{2}}\right)\).Hence:
At least 75% of women have platelet counts that are within 2 standard deviations of the mean.
Considering the mean and the standard deviation, the amounts are given as follows:
255.1 - 2 x 65.3 = 124.5 cells/uL.255.1 + 2 x 65.3 = 385.7 cells/uL.Hence:
The minimum possible platelet count within 2 standard deviations of the mean is of 124.5 cells/uL and the maximum is of 385.7 cells/uL.
More can be learned about Chebyshev's Theorem at https://brainly.com/question/5179184
#SPJ1
How do I solve 12a+3c=2a+6, for a
Answers
Answer:
14a+9c
Step-by-step explanation:
Answer:
Step-by-step explanatio

Eighth grade > V.4 Area and circumference of circles CHV
The circumference of a circle is 43.332 miles. What is the circle's diameter?
Use 3.14 for .
Answers
Answer: \(D=13.8\)
Step-by-step explanation:
To fing the diameter of a circle when given the circumfrence we use the formula of
\(D=\frac{c}{\pi }\)
\(D= \frac{43.332}{3.14}\)
\(D=13.8\)
help me baaaaaaaaaaaaaaaalls

Answers
aaaaa
Answer:
The correct scale faction the first pentagon dilated by to create the second pentagon is 1.25.
Step-by-step explanation:
Since the second pentagon is a dilation of the first pentagon, we can conclude these pentagons are similar, meaning the shape retained all of its previous angles, and all the corresponding sides are dilated by a common scale factor. Since we know the values of a pair of corresponding sides, we can use those to find the scale factor of dilation.
The corresponding side of the original pentagon is 4 units, and the corresponding side of the dilated pentagon is 5 units. Since the first pentagon dilated to become the second, in order to solve the scale factor the pentagon dilated by, we'd have to divide the side given on the second pentagon by the corresponding side of the first, which will be 5 ÷ 4 = 1.25. Therefore, that will be the scale factor the pentagon dilated by.
Have a great day! Feel free to let me know if you have any more questions :)
what should be the first step in adding these equation to eliminate y 12x - 2y = -1 + 4x + 6y =-4
Answers
Answer:
See below
Step-by-step explanation:
Assumed you need to solve the system:
12x - 2y = - 14x + 6y = - 4In order to solve this by elimination, triple the first equation and add the second one.
It will make the coefficients of y same with opposite signs:
-6y and 6yWhen added together these cancel, leaving x as the only variable.
6th grade math
9x + 8w - 2x + w
Answers
Answer: 7x + 9w if you are just simplifying
Step-by-step explanation:
Homework: Section 11.1 Question 7. Complete the square to find the x-intercepts of the function given by the equation listed. f(x)=x² +34x+104 What are the x-intercepts? **** (Simplify your answer. T
Answers
Answer:
x² + 34x + 104 = 0
x² + 34x = -104
x² + 34x + ((1/2)(34))² = -104 + ((1/2)(34))²
x² + 34x + 17² = -104 + 17²
x² + 34x + 289 = 185
(x + 17)² = 185
x + 17 = +√185
x = -17 + √185
Write a story that can be represented using the equation y=x+1/5x
Answers
A story that can be represented using the equation y=x+1/5x is "John has an apple and he cut another apple into 5 equal parts and took on part. What's the rural fraction of apple that he has?
How to illustrate the equation?An equation is the statement that illustrates the variables given. In this case, two or more components are taken into consideration to describe the scenario. It is vital to note that an equation is a mathematical statement which is made up of two expressions that are connected by an equal sign.
In this case, if John has an apple and he cut another apple into 5 equal parts and took on part.
This can be illustrated as:
y = x + 1/5x
Learn more about equations on:
brainly.com/question/2972832
#SPJ1
PLS HELP ME I have to get this in by 11:59
Explain why 0.5 times 3.4 has only one decimal place in the product.
It sounds pretty easy but it isn’t
Answers
The reason why 0.5 times 3.4 has only one decimal place in the product is because the second decimal number is zero.
What is the reason why one decimal is been displaced in the calculation?The concept that will be used to calculate this question is the concept of decimal point.
It was given that 0.5 times 3.4 will equal 1.7, the result shows only one decimal which is been given between 1 and 7 and the reason for this is that the other decimal is zero, and it is displace by the calculator, it will make no sense.
Learn more about decimal here: https://brainly.com/question/28338004
#SPJ1
the manager of a cleaning supply store wants to estimate the actual amount of bleach contained in 1-gallon bottles purchased from a nationally known brand manufacturer. the manufacturer’s specifications state that the standard deviation of the amount of bleach is equal to 0.02 gallon. a random sample of 64 bottles is selected. the sample mean amount of bleach per 1-gallon bottle is 0.992 gallon.
Answers
The population mean amount of paint included in a 1- gallon can is between 0.160 gallons to 1.814 gallons.
Confidence Intervals:The confidence intervals (range estimates) over a specific level of confidence are excellent indicators for the true value of the parameter. The primary logic for computing the estimate is by means of point estimate and margin of error.
The confidence level is 99%
The significance level is 0.01 \((\alpha )\)
The z - table is used to obtain two - tailed critical value at 0.01 level of significance
\(2P(Z > z_\frac{\alpha }{2} )=\frac{\alpha }{2}\)
2P(Z > 2.58) = 0.01
The margin of error1 is:
ME = \(z_\frac{\alpha }{2} .(\frac{\sigma}{\sqrt{n} } )\)
ME = 2.58 \((\frac{2.58}{\sqrt{64} } )\)
ME = 0.832
The 99% confidence interval for the population mean amount of paint include in a 1- gallon can:
(x(bar) - ME ,x(bar) + ME ) = (0.992 - 0.832 , 0.992 + 0.832)
= (0.160 , 1.814)
Therefore, the population mean amount of paint included in a 1- gallon can is between 0.160 gallons to 1.814 gallons.
Learn more about confidence level at:
https://brainly.com/question/22851322
#SPJ4
Find an equation of the line containing the point (2,-5) and parallel to y = – 4x – 2.
Write your answer in slope-intercept form.

Answers
Answer:
the desired equation is y = – 4x + 3
Step-by-step explanation:
Parallel lines have the same slope and thus similar equations. Thus, the equation of a line parallel to the given line has the form y = – 4x + C. We need only find C.
The new line goes through (2, -5), and so we substitute 2 for x and -5 for y to obtain
-5 = – 4(2) + C. Then -5 + 8 = C, or C = 3.
Then the desired equation is y = – 4x + 3
jim walked 1/2 of a mile in 1/4 of an hour. at this rate how long will it take him to walk one mile
Answers
Answer:
1/4=25 minutes an hour
25×2=50
it will take him 50 minutes
At the end of 1st Quarter of 2009 the median price of a single-family home in Charleston/No. Charleston was $184,990. Single-family home prices in Charleston/No. Charleston decreased from the 1st Qtr of 2008 by 8.15%. NOTE: Depreciation means a negative value for r. (a). Estimate the median price of a single-family home in the 1st Qtr of 2008.
(b). If the median price of a single-family home falls at the same rate for the next 2 years, estimate the median price of a single-family home in the 1st Qtr of 2011.
Answers
The estimated median price of a single-family home in Charleston/No. Charleston in the 1st Quarter of 2008 is $201,048. If the median price continues to decrease at the same rate for the next two years, the estimated median price of a single-family home in the 1st Quarter of 2011 would be $144,458.
(a) To estimate the median price of a single-family home in the 1st Quarter of 2008, we need to calculate the original price before the 8.15% decrease. Let's assume the original price was P. The price after the decrease can be calculated as P - 8.15% of P, which translates to P - (0.0815 * P) = P(1 - 0.0815). Given that the end of 1st Quarter of 2009 median price was $184,990, we can set up the equation as $184,990 = P(1 - 0.0815) and solve for P. This gives us P ≈ $201,048 as the estimated median price of a single-family home in the 1st Quarter of 2008.
(b) If the median price of a single-family home falls at the same rate for the next two years, we can calculate the price for the 1st Quarter of 2011 using the estimated median price from the 1st Quarter of 2009. Starting with the median price of $184,990, we need to apply an 8.15% decrease for two consecutive years. After the first year, the price would be $184,990 - (0.0815 * $184,990) = $169,805.95. Applying the same percentage decrease for the second year, the price would be $169,805.95 - (0.0815 * $169,805.95) = $156,012.32. Therefore, the estimated median price of a single-family home in the 1st Quarter of 2011 would be approximately $144,458.
To learn more about median click here: brainly.com/question/300591
#SPJ11
help! i can’t figure it out
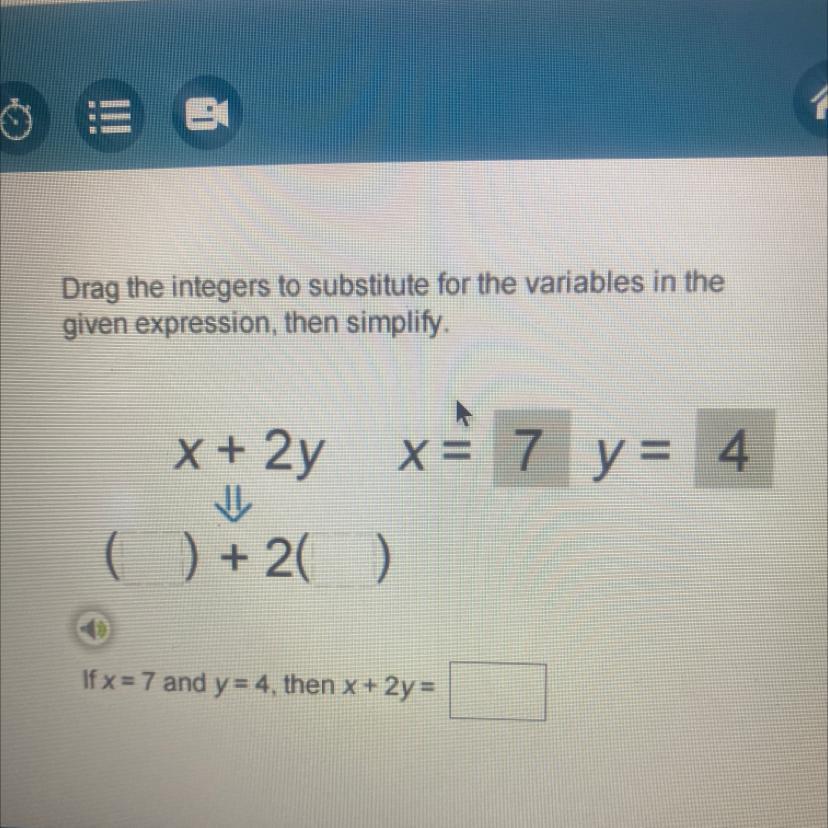
Answers
Answer:
15
Step-by-step explanation:
x + 2y
Putting x = 7, y = 4, we have
7 + 2(4)
= 7 + 8
= 15
Hope it helps.
If you have any query, feel free to ask.
Step-by-step explanation:
It's saying x = 7 and y = 4, which means everywhere there is an x, you'll place a 7 and everywhere there is a y, you'll place a 4
x + 2y turns into (7) + 2(4)
Now we can answer the bottom question
2(4) = 8
7 + 8 = 15
so...
If x =7 and y=4, then x+2y= 15
Given f(x) = –3x – 4, find f(–5).
Answers
Answer:
3x
Step-by-step explanation:
because if f is -5, -5=-3x-4, -5+4, -1=-3 divide and get 3=x
What is the percent
increase from 70 to 77?
Answers
Percentage change = 10%
We can use the formula:
Percent change = \(\frac{New-Old}{Old}\) x 100
Percent change = \(\frac{77-70}{70}\)x100
Percent change = \(\frac{7}{70}\) x 100
Percent change = 0.1 x 100
Percent change = 10%
Answer: 53.9
Step-by-step explanation:
Which of the following expressions are equivalent to x - (-x) + y?
Choose all the answers that apply.
A. 0+y
B. y
C. None of the above
Answers
The expression equivalent to x - (-x) + y is 2x + y.
The correct option is (C) None of the above
What is expression?An expression is a combination of numbers, variables, functions (such as addition, subtraction, multiplication or division etc.)
Given:
x - (-x) + y
=x +x +y
= X(1+1) + y
= x(2) + y
= 2x + y
Hence, the equivalent expression is 2x + y.
Learn more about expression here:
https://brainly.com/question/14083225
#SPJ1
I’m stuck lol help please

Answers
Answer:
Step-by-step explanation:
9994ddaefeaf
which expression is equal to sin w

Answers
Answer:
A. Cos S
Step-by-step explanation:
Recall: SOH CAH TOA
Sin W = Opp/Hyp
Opposite = 4
Hypotenuse = 5
Sin W = 4/5
Let's find the ratio for each option given to determine which gives us the same ratio as Sin W.
Option A: Cos S
Cos S = Adj/Hyp = 4/5
Option B: tan W
Tan W = Opp/Adj = 4/3
Option C: cos W
Cos W = Adj/Hyp = 3/5
Option D: sin S
Sin S = Opp/Hyp = 3/5
✔️Thus, sin W = cos S = 4/5
The correct option is A
what is the area of the shape, respond if you love your mom

Answers
Answer:
162m
Step-by-step explanation:
(8x14)+ (10x5) =162m
112 + 50 = 162m
Answer:
162m
Step-by-step explanation:
Write the equation of the line represented by y - 3 = 2(x + 5) in slope-intercept form. y = X +
Answers
Answer:
y = 2x + 13
Step-by-step explanation:
Sierra is ordering supplies for her restaurant. She has ordered 5 pounds of beel du
$9.25 per pound, 3 pounds of onions at $6.35 a pound, 6 pounds of pinto beans at
$3.82. She is planning on preparing 15 burritos. If Sierra charges $3.72 per burrito
OTOVO
42 (5 points)
will she make money or lose money? How
3.72
Answers
1, 4, 9, 16, 25, ______, ______, ______
Answers
suppose this player attempts 10 shots in a game and makes only 3 of them. does this provide convincing evidence that she is less than a 47% shooter?
Answers
No, because it is plausible that she would make 3 or fewer shots by chance alone.
What is convincing evidence?
The proof is sufficient evidence or a sufficient argument for the truth of a proposition. The concept applies in a variety of disciplines, with both the nature of the evidence or justification and the criteria for sufficiency being area-dependent.
if our test statistic is: positive and greater than the critical value, then we have sufficient evidence to reject the null hypothesis and accept the alternative hypothesis. positive and lower than or equal to the critical value, we must accept the null hypothesis.
To learn more about convincing evidence visit:
https://brainly.com/question/8394382
#SPJ4
Joe bought a box of laundry detergent that contains 195 scoops. Each load of laundry uses 2.5 scoops. How many loads of laundry can he do with this one box? The box of detergent was $19.99. How much is he paying for each load that he washes? Round to the nearest hundredths place.
Answers
Answer:
-Joe can do 78 loads of laundry with this one box.
-He is paying $0.25 for each load that he washes.
Step-by-step explanation:
To determine the number of loads of laundry that Joe can do with this one box, you have to divide the total amount of scoops in a box by the amount of scoops that each load of laundry uses:
195/2.5=78
This means that Joe can do 78 loads of laundry with this one box.
Now, to find the amount that he is paying for each load that he washes, you have to divide the cost of the box of detergent by the amount of loads of laundry you can do with one box:
19.99/78=0.25
According to this, he is paying $0.25 for each load that he washes.
Suppose that f and g are differentiable at x 0
,f(x 0
)=g(x 0
)=0, and g ′
(x 0
)
=0. Without using L'Hospital's rule, show that lim x→x 0
g(x)
f(x)
= g ′
(x 0
)
f ′
(x 0
)
. b) State the corresponding results for one-sided limits.
Answers
To prove the limit identity without using L'Hospital's rule, we can utilize the definition of the derivative and properties of limits.
a) For the limit lim_(x→x₀) g(x)/f(x), where f and g are differentiable at x₀, and f(x₀) = g(x₀) = 0, and g'(x₀) ≠ 0, we want to show that this limit is equal to g'(x₀)/f'(x₀).
We can rewrite the expression as:
g(x)/f(x) = [g(x) - g(x₀)] / [f(x) - f(x₀)]
Using the Mean Value Theorem, we know that for any differentiable function h(x) on an interval containing x₀, there exists a point c between x and x₀ such that:
h(x) - h(x₀) = h'(c) * (x - x₀)
Applying this to g(x) and f(x), we have:
g(x) - g(x₀) = g'(c) * (x - x₀)
f(x) - f(x₀) = f'(c) * (x - x₀)
Note that as x approaches x₀, c also approaches x₀. Therefore, we can rewrite the expression as:
lim_(x→x₀) g(x)/f(x) = lim_(x→x₀) [g'(c) * (x - x₀)] / [f'(c) * (x - x₀)]
Now, we can simplify the expression:
lim_(x→x₀) g(x)/f(x) = g'(c)/f'(c) * lim_(x→x₀) (x - x₀)/(x - x₀)
Since g'(c) and f'(c) are constants (as c approaches x₀), we can take them out of the limit:
lim_(x→x₀) g(x)/f(x) = g'(c)/f'(c) * lim_(x→x₀) 1
As x approaches x₀, the limit on the right side becomes 1:
lim_(x→x₀) g(x)/f(x) = g'(c)/f'(c) * 1
Since c approaches x₀, we can rewrite g'(c)/f'(c) as g'(x₀)/f'(x₀):
lim_(x→x₀) g(x)/f(x) = g'(x₀)/f'(x₀)
Hence, we conclude that:
lim_(x→x₀) g(x)/f(x) = g'(x₀)/f'(x₀)
b) For one-sided limits, we have:
For the limit lim_(x→x₀⁺) g(x)/f(x), the result would still be g'(x₀) / f'(x₀), assuming all the conditions mentioned in part a) hold true.
For the limit lim_(x→x₀⁻) g(x)/f(x), the result would still be g'(x₀) / f'(x₀), assuming all the conditions mentioned in part a) hold true.
These results hold because the definition and properties of one-sided limits are similar to those of two-sided limits, and the reasoning used in part a) applies to both one-sided limits as well.
Therefore, the corresponding results for one-sided limits are g'(x₀) / f'(x₀) in both cases.
Learn more about differentiation here:
brainly.com/question/13958985
#SPJ11
without actually solving the given differential equation, find the minimum radius of convergence r of power series solutions about the ordinary point x = 1. (x^2 - 2x + 17)y"+ xy' -4y = 0
Answers
Power series solutions have a minimum radius of convergence of R of 10.0498 around the normal point x = 0 and 10 units around the normal point x=1.
What is a differential equation?A differential equation in mathematics is an equation that connects the derivatives of one or more unknown functions.
Applications often involve functions that reflect physical quantities, derivatives that depict the rates at which those values change, and a differential equation that establishes a connection between the three.
The given equation: \(\left(x^2-2 x+26\right) y^{\prime \prime}+x y^{\prime}-4 y=0\)
It is necessary to determine the power series solutions' minimal radius of convergence R around the typical points x = 0 and x = 1.
The separation between the ordinary point and the differential equation's singularity is now the minimal radius of convergence.
The polynomial's root, which is connected to the second derivative, is the singularity point.
The singularity points will be determined as follows:
\(\begin{aligned}& x^2-2 x+26=0 \\& x=\frac{-b \pm \sqrt{b^2-4 a c}}{2 a} \\& x=\frac{2 \pm \sqrt{(-2)^2-4 \times 1 \times 26}}{2} \\& x=1 \pm \sqrt{-100} \\& x=1 \pm 10 i\end{aligned}\)
In this case, x1 = 1+10i and x2 = 1-10i are the singularity sites.
The ordinary points at this time are z1 = 0+01 and z2 = 1+0i.
One can compute the minimum radius of convergence using the formula:
\(\begin{aligned}& r_1=\left|z_1-x_1\right| \\& =|0+0 i-1-10 i| \\& =\sqrt{101} \\& =10.0498 \\& r_2=\left|z_2-x_1\right| \\& =\sqrt{100} \\& =10\end{aligned}\)
Therefore, power series solutions have a minimum radius of convergence of R of 10.0498 around the normal point x = 0 and 10 units around the normal point x = 1.
Know more about differential equations here:
https://brainly.com/question/1164377
#SPJ4