The length of a rectangle is 8cm more than its width the perimeter of the rectangle is 96cm what are the dimensions of the rectangle?
Answers
Step-by-step explanation:
96/8=__________ will be the answer
Related Questions
Wyatt mows lawns to earn money. He charges by the area
of the yard. A new customer has a yard in the shape of a
triangle with a base of 200 feet and a height of 70 feet.
What is the area of the yard?
4,667 ft?
540 ft?
7,000 ft
270 ft?
Answers
area of triangle formula=1/2*base*height
The area of the triangular yard is 7000 ft².
What is the area of a triangle?The entire area enclosed by three sides of a triangle is the area of it.
Given,
The base of the triangle is 200 feet and the height of the triangle is 70 feet.
Therefore, the area of the triangle
= (1/2) × base of the triangle × height of the triangle = (1/2) × 200 × 70 ft² = 7000 ft².
Learn more about the area of a triangle here: https://brainly.com/question/22625791
#Tag #SPJ2
3log2-5logx
Condense
Show all work
URGENT
Answers
Answer: To condense the expression 3log2 - 5logx, we can use the logarithmic properties, specifically the product rule and power rule of logarithms.
The product rule states that alogb + clogb = logb((b^a) * (b^c)), and the power rule states that alogb = logb(b^a).
Applying these rules, let's condense the given expression step by step:
3log2 - 5logx
Applying the power rule to log2: log2(2^3) - 5logx
Simplifying: log2(8) - 5logx
log2(8) can be further simplified as log2(2^3) using the power rule: 3 - 5logx
Therefore, the condensed form of the expression 3log2 - 5logx is 3 - 5logx.
is this an increasing or decreasing exponential function? How can you tell based on its equation?
Answers
The given equation, y = -1/7x + 1, represents a decreasing linear function, not an exponential function, because it has a negative slope (-1/7).
How can we determine if a linear function is increasing or decreasing based on its equation?The given equation, y = -1/7x + 1, represents a linear function rather than an exponential function. It is a linear equation in the form y = mx + b, where m is the slope (-1/7) and b is the y-intercept (1).
Linear functions have a constant slope, which determines whether the function is increasing or decreasing. In this case, the slope is negative (-1/7), indicating that the line has a downward (decreasing) direction. As x increases, y decreases at a constant rate.
Therefore, based on the equation y = -1/7x + 1, we can determine that the function represents a line with a decreasing trend rather than an exponential function.
Learn more about linear
brainly.com/question/26139696
#SPJ11
If the probability of a newborn child being female is 0.5, find the probability that in 50 births, 35 or more will be female. Use the normal distribution to approximate the binomial distribution.
Answers
The likelihood (probability) that in 50 births, 35 or more will be female is around 0.0023.
To fathom this issue, ready to utilize the ordinary(normal) estimation of the binomial conveyance.
The cruel(mean) of binomial dissemination with parameters n and p is np, and the fluctuation is np(1-p).
Hence, for 50 births with a likelihood of 0.5 of being female, the cruel(mean) is 500.5 = 25 and the fluctuation is 500.5*(1-0.5) = 12.5.
We need to discover the probability that 35 or more births will be female. We are able to utilize the typical guess to gauge this likelihood.
We begin with standardizing the dissemination by subtracting the cruel and isolating by the standard deviation, which is the square root of the change:
z = (35 - 25) / √(12.5) = 2.828
We at that point utilize a standard ordinary dissemination table or calculator to discover the likelihood that z is more prominent than or breaks even with 2.828.
This likelihood is roughly 0.0023.
Hence, the likelihood that in 50 births, 35 or more will be female is around 0.0023.
To know more about probability refer to this :
https://brainly.com/question/24756209
#SPJ4
I NEED HELP ASAP ! THIS IS FOR A PAST DUE QUIZ. THEY ARE GIVING ME ONE MORE CHANCE
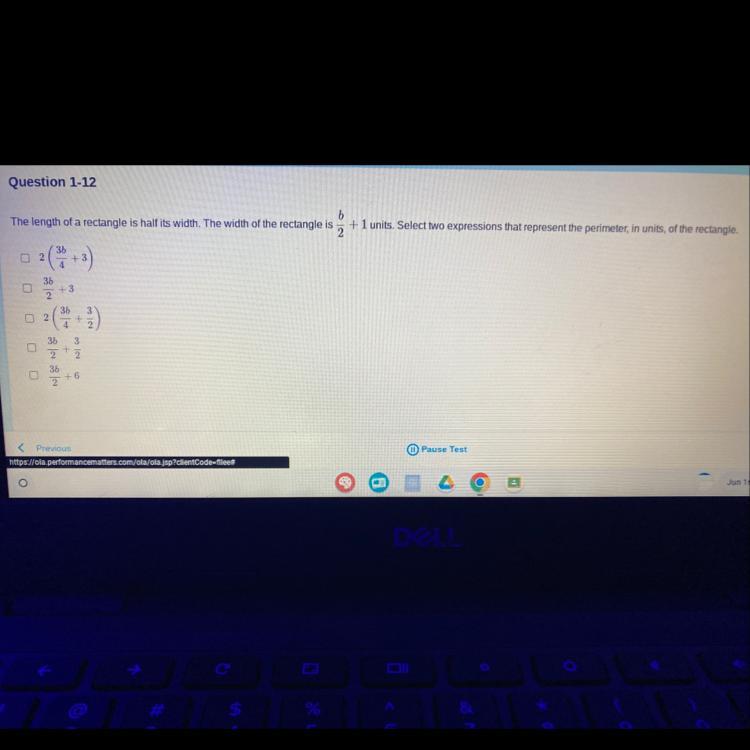
Answers
Answer:
3b/2 + 3
Step-by-step explanation:
The formula to calculate perimeter of rectangle is 2l + 2w
The length is half the width so length is 1/2 (b/2 +1), which when simplified is b/4 + 1/2
Using the formula to calculate perimeter you can substitute and calculate
p= 2l + 2w
p= 2(b/4 + 1/2) + 2(b/2 + 1)
p= 2b/4 +2/2 + 2b/2 +2
p= 1/2b + 1 + b + 2
p= 3/2b + 3
Simplified it's 3b/2 +3
11-2(3m-10)=5(4-m)
note: pls show the steps pls
Answers
Answer:
m=11
Step-by-step explanation:
11-2(3m-10)=5(4-m)
11-6m+20=20-5m
11+20=20+m
11=m
If x and y are positive numbers with x>y, show that a triangle with sides of lengths 2xy, x^2-y^2, and x^2+y^2 and is always a right triangle?
Answers
Answer: 2xy
Step-by-step explanation: We know that x%5E2+%2B+y%5E2 must be the longest side of the triangle (it cannot be 2xy, I will demonstrate why afterwards). By the Pythagorean theorem,
. Therefore this is a right triangle.
The only "assumption" we had to make was that x%5E2+%2B+y%5E2+%3E+2xy, but this is easy to prove. By the AM-GM inequality, %28x%5E2+%2B+y%5E2%29%2F2+%3E=+sqrt%28x%5E2y%5E2%29+=+xy. Multiplying both sides by 2, x%5E2+%2B+y%5E2+%3E=+2xy. Equality occurs only when x+=+y, but this cannot be true, so x%5E2+%2B+y%5E2 is strictly greater than 2xy.
solve the differential equation by variation of parameters. y'' y = sec() tan()
Answers
The general solution of the differential equation y''(x) + y(x) = sec(x) tan(x) is y(x) = c₁cos(x) + c₂sin(x) + (-ln|sec(x) + tan(x)| + C₁)cos(x) + (-ln|sec(x) + tan(x)| + C₂)sin(x); here c₁ and c₂ are constants.
To solve the differential equation y''(x) + y(x) = sec(x) tan(x) using variation of parameters, we first need to find the solutions to the homogeneous equation y''(x) + y(x) = 0.
The auxiliary equation for the homogeneous equation is r² + 1 = 0, which has complex roots r = ±i.
The corresponding solutions to the homogeneous equation are y₁(x) = cos(x) and y₂(x) = sin(x).
Next, we need to find the particular solution using the method of variation of parameters. Let's assume the particular solution has the form y_p(x) = u(x)cos(x) + v(x)sin(x).
Now, we need to find u(x) and v(x) by substituting this form into the original differential equation and solving for u'(x) and v'(x).
Differentiating y_p(x), we get y_p'(x) = u'(x)cos(x) - u(x)sin(x) + v'(x)sin(x) + v(x)cos(x).
Taking the second derivative, y_p''(x) = -u(x)cos(x) - u'(x)sin(x) + v(x)sin(x) + v'(x)cos(x).
Substituting these derivatives into the original differential equation, we have:
(-u(x)cos(x) - u'(x)sin(x) + v(x)sin(x) + v'(x)cos(x)) + (u(x)cos(x) + v(x)sin(x)) = sec(x)tan(x).
Simplifying, we get:
u'(x)sin(x) + v'(x)cos(x) = sec(x)tan(x).
To find u'(x) and v'(x), we solve the following system of equations:
u'(x)sin(x) + v'(x)cos(x) = sec(x)tan(x),
u(x)cos(x) + v(x)sin(x) = 0.
We can solve this system using various methods such as substitution or elimination.
Solving the system, we find:
u'(x) = sin(x)sec(x),
v'(x) = -cos(x)sec(x).
Integrating these expressions, we obtain:
u(x) = -ln|sec(x) + tan(x)| + C₁,
v(x) = -ln|sec(x) + tan(x)| + C₂.
Finally, the particular solution is given by:
y_p(x) = (-ln|sec(x) + tan(x)| + C₁)cos(x) + (-ln|sec(x) + tan(x)| + C₂)sin(x).
The general solution to the differential equation is the sum of the homogeneous and particular solutions:
y(x) = c₁cos(x) + c₂sin(x) + (-ln|sec(x) + tan(x)| + C₁)cos(x) + (-ln|sec(x) + tan(x)| + C₂)sin(x).
Here, c₁ and c₂ are constants.
Learn more about differential equation here:
https://brainly.com/question/25731911
#SPJ11
Can someone show the work on this problem

Answers
Answer:
4.69 in
Step-by-step explanation:
By sine rule:
\( \frac{ \sin \: 23 \degree}{a} = \frac{ \sin \: 90 \degree}{12} \\ \\ \frac{ \sin \: 23 \degree}{a} = \frac{1}{12} \\ \\ a = 12 \: \sin 23 \degree \\ \\ a = 12 \times 0.3907311285 \\ \\ a = 4.68877354 \\ \\ a \approx 4.69\: in\)
Expand and simplify 2(3t+4)+3(2t+6)
Answers
for each sequence given find a closed formula for an, assume the first term is always a0. 2, 5, 14, 29, 50, 77
Answers
The closed formula for the sequence is an = n^2 + n + 2.
The given sequence is not arithmetic, nor is it geometric, but we can find a pattern in the differences between successive terms to find a formula.
The first differences are 3, 9, 15, 21, 27, which suggests that the second differences are all equal to 6. This means that the original sequence can be modeled by a quadratic equation of the form:
an = an-1 + (an-1 - an-2) + 6
with a0 = 2 and a1 = 5.
Using this recursive formula, we can find the next terms of the sequence:
a2 = a1 + (a1 - a0) + 6 = 14
a3 = a2 + (a2 - a1) + 6 = 29
a4 = a3 + (a3 - a2) + 6 = 50
a5 = a4 + (a4 - a3) + 6 = 77
Therefore, the closed formula for the sequence is:
an = n^2 + n + 2.
Learn more about sequence here
https://brainly.com/question/7882626
#SPJ11
a
4.375 seconds
b
3.875 seconds
c
3.625 seconds
d
3.75 seconds

Answers
The vertex is (3,147), which means that the final answer is that the maximum height of the ball is 147 feet.
What is function ?
The first thing to recognize here is that the graph of your function is a parabola. You can tell it opens downward, as the coefficient in-front for the t^2 term is negative. That means our parabola's vertex will be the maximum y-value (vs the vertex being the minimum y-value if the parabola opened up). This is what we are trying to solve - the maximum height of the ball.
For a parabola, y = ax^2 + bx + c, the vertex at point (h,k), is first found by the equation h = -b / 2a, and then plugging that point into the equation to find k.
So let's solve for h in this problem. Given the equation y = -16t^2 + 96t + 3, we know a = -16, b = 96, c = 3.
h = -b/2a
h = -(96) / 2(-16)
h = -96 / -32
h = 3 seconds
This means the the ball will reach it's maximum height after 3 seconds. But the problem is asking is for what that height is. So for our final step, let's plug in t=3 to our equation:
y = -16t^2 + 96t + 3
y = -16*(3)^2 + 96*(3)+ 3
y = -144 + 288 + 3
y = 147 feet
We have now found the vertex is (3,147), which means that the final answer is that the maximum height of the ball is 147 feet.
To learn more about vertex visit:https://brainly.com/question/29030495
#SPJ1
The way an individual perceives stimuli and the general manner in which he or she responds to it is a __________-_______ style
Answers
Answer:
decision-making
Step-by-step explanation:
An equation is shown. Select all the ways you can use the Distributive property to find the missing factors. 7 X 3 = (___ X 3 ) + (____ X 3)7 X 3 = ( 5 X 3 ) + ( 2 X 3 )7 X 3 = ( 2 X 3 ) + ( 5 X 3 )7 X 3 = ( 7 X 3 ) + ( 1 X 3 )7 X 3 = ( 1 X 3 + ( 6 X 3 )7 X 3 = ( 6 X 3 ) + ( 1 X 3 )3rd grade student
Answers
We need to use distributive property to find the missing factors:
\(7\cdot3\text{ = 7+7+7 = 21}\)"The distributive property of multiplication says that a multiplication fact can be broken up into the sum of two other multiplication facts."
\(7\cdot3=(5+2)\cdot3\)because 5+2 = 7.
\((5+2)\cdot3\text{ = (5}\cdot3)+(2\cdot3)\)So the correct answer are:
7 X 3 = ( 5 X 3 ) + ( 2 X 3 )
Then
7 X 3 = ( 2 X 3 ) + ( 5 X 3 )
because:
( 5 X 3 ) + ( 2 X 3 ) = ( 2 X 3 ) + ( 5 X 3 )
Also :
7 X 3 = ( 1 X 3) + ( 6 X 3 )
Because 7 x3 = (6+1) x 3 = 1 X 3) + ( 6 X 3 )
Karina uses the system of equations below to compare the monthly utility costs in July and December for electricity, x, and natural gas, y. 750x + 17y = 141.61 300x + 30y = 75.90 Karina solves the system using linear combination and arrives at the equation 116y = 96.28. She then solves this equation for y. Which statement explains Karina’s solution?
Answers
Answer:
d. The cost of natural gas (y) = $0.83 per unit
Step-by-step explanation:
The explanation is shown below:-
the equation of system is:
750x + 17y = 141.61 (i)
300x + 30y =75.90 (ii)
as x indicates the cost of electricity and y indicates the costs of natural gas.
we will solve the both equation with the help of multiplication for (i) by 30 and for (ii) 75
\(30\times (750x + 17y) 30\times 141.61\\\\\)
after solve the above equation we will get
22,500x + 510y = 4248.3 (iii)
\(75\times (330x + 30y) = 75\times 75.90\)
after solve the above equation we will get
22500x + 2250y = 5692.5 (iv)
After deducting the equation (iii) and (iv) we will get
1740 y = 1444.2
After Dividing by 15 both sides,
116y = 96.28
So, Katrina simplify the above system using linear equation and reach at the equation that is
116 y = 96.28
By Division property of equality defines that divide the equal no. of both sides of an equation:
by Division of 116 to both sides of an equation, to get y:
\(\frac{116y}{116} = \frac{96.28}{116}\)
y = 0.83
So, the natural gas is $0.83 per unit
Answer:
d
Step-by-step explanation:
HELLOO!! I really need to have this answered. Please help me!! Thank you!!!

Answers
Answer:
Step-by-step explanation:
The first one is equal to. 203/203 is equal to 1. 1 times any number is itself.
The second on is less than. 9/37 is a proper fraction and when a number is multiplied by a proper fraction, it gets smaller.
An ordinary deck of 52 cards is randomly divided into 4 piles of 13 each. What is the probability that all piles have exactly one Ace?
Answers
The probability that all four piles have exactly one Ace is 1 / (13 * 17 * 50 * 49), which is approximately 0.00014424.
To find the probability that all four piles have exactly one Ace, we can consider the number of ways to distribute the Aces and the total number of possible distributions.
There are 4 Aces in the deck, and each pile should receive exactly one Ace. The first Ace can be placed in any of the 52 cards, the second Ace in any of the remaining 51 cards, the third Ace in any of the remaining 50 cards, and the fourth Ace in any of the remaining 49 cards.
So, the total number of possible distributions is 52 * 51 * 50 * 49.
To calculate the probability, we need to divide the number of favorable outcomes (where all piles have exactly one Ace) by the total number of possible distributions.
Since each Ace can be distributed to any of the 4 piles, the number of favorable outcomes is 4 * 3 * 2 * 1.
Therefore, the probability is (4 * 3 * 2 * 1) / (52 * 51 * 50 * 49), which simplifies to 1 / (13 * 17 * 50 * 49).
To learn more about probability refer here:
https://brainly.com/question/31120123#
#SPJ11
A surveyor measures the lengths of the sides of a triangular plot of land. what is the measure of the angle of the triangular plot at which the surveyor stands? approximate to the nearest degree. cosâ€""1(0.75) = 41° cosâ€""1(0.125) = 83° cosâ€""1(0.563) = 56° cosâ€""1(0.15) = 89°
Answers
The surveyor determines the angle of the triangular plot by using the inverse cosine function with a given value of cos⁻¹(0.15). The result of approximately 89° represents the approximate measure of the angle at which the surveyor stands in relation to the sides of the plot.
Among the given options for the inverse cosine values, the measure of the angle of the triangular plot at which the surveyor stands is determined by the value of cos⁻¹(0.15), which is approximately 89°.
Each result represents the measure of the angle at which the surveyor stands in relation to the sides of the triangular plot. It's important to note that these results are approximate values rounded to the nearest degree.
By using the given cosine values and applying the inverse cosine function, the surveyor can determine the approximate angle of the triangular plot.
Therefore, The approximate measure of the angle of the triangular plot at which the surveyor stands is 89°.
Learn more about angle here:
https://brainly.com/question/25716982
#SPJ11
Question-
A surveyor measures the lengths of the sides of a triangular plot of land. what is the measure of the angle of the triangular plot at which the surveyor stands? Approximate to the nearest degree.
cos^(-1)(0.75) ≈ 41°
cos^(-1)(0.125) ≈ 83°
cos^(-1)(0.563) ≈ 56°
cos^(-1)(0.15) ≈ 89°
the car is traveling along the road with a speed of v=(2s) m/s, where s is in meters.
Answers
The tangential and normal components of the acceleration when s = 10 m is 40 m/s^2 and 8 m/s^2 respectively.
In the given question, a car is travelling along the road with a speed of 2s m/s, where s is in meters.
We have to determine the tangential and normal components of the acceleration when s = 10 m.
Speed (v) = 2s
Motion is circular so, Radius of circle = 50m
Tangential acceleration = dv/dt
Tangential acceleration = d(2s) / dt
Tangential acceleration = 2(ds)/dt
Tangential acceleration = 2v
Tangential acceleration = 2(2s)
Tangential Acceleration = 4s
As given s = 10 m
Tangential acceleration = 4 x 10
Tangential acceleration = 40 m/s^2
Normal acceleration = v^2/ r
Normal acceleration = 4s^2/r
Normal acceleration = {4 x 10^2}/50
Normal acceleration = {4 x 100}/50
Normal acceleration = 400/50
Normal acceleration = 8 m/s^2
To learn more about Tangential and normal acceleration link is here
brainly.com/question/30029917
#SPJ4
The complete question is:
A car is travelling along the road with a speed of 2s m/s, where s is in meters. Determine the tangential and normal components of the acceleration when s = 10 m. Treat the car as a particle

For a recent paint job, Josh mixed red and white paint to make two different shades of pink. When the job was done, Josh ended up with leftover paint: 5 gallons of dark pink paint (80% red) and 4 gallons of light pink paint (30% red). Josh wants to make a medium pink color (50% red) to paint his daughter's bedroom. He will need 3 gallons to completely cover the walls. How much of each of the leftover paints should Josh mix to achieve his desired color?
? gallons of dark pink paint
? gallons of light pink paint
Answers
Josh should mix 1.2 gallons of dark pink paint and 1.8 gallons of light pink paint to achieve the desired medium pink color.
To find out how much of each leftover paint Josh should mix to achieve a medium pink color (50% red), we can set up a system of equations based on the percentages of red in the paints.
Let's assume that Josh needs x gallons of dark pink paint and y gallons of light pink paint to achieve the desired color.
The total amount of paint needed is 3 gallons, so we have the equation:
x + y = 3
The percentage of red in the dark pink paint is 80%, which means 80% of x gallons is red. Similarly, the percentage of red in the light pink paint is 30%, which means 30% of y gallons is red. Since Josh wants a 50% red mixture, we have the equation:
(80/100)x + (30/100)y = (50/100)(x + y)
Simplifying this equation, we get:
0.8x + 0.3y = 0.5(x + y)
Now, we can solve this system of equations to find the values of x and y.
Let's multiply both sides of the first equation by 0.3 to eliminate decimals:
0.3x + 0.3y = 0.3(3)
0.3x + 0.3y = 0.9
Now we can subtract the second equation from this equation:
(0.3x + 0.3y) - (0.8x + 0.3y) = 0.9 - 0.5(x + y)
-0.5x = 0.9 - 0.5x - 0.5y
Simplifying further, we have:
-0.5x = 0.9 - 0.5x - 0.5y
Now, rearrange the equation to isolate y:
0.5x - 0.5y = 0.9 - 0.5x
Next, divide through by -0.5:
x - y = -1.8 + x
Canceling out the x terms, we get:
-y = -1.8
Finally, solve for y:
y = 1.8
Substitute this value of y back into the first equation to solve for x:
x + 1.8 = 3
x = 3 - 1.8
x = 1.2
Therefore, Josh should mix 1.2 gallons of dark pink paint and 1.8 gallons of light pink paint to achieve the desired medium pink color.
for such more question on medium
https://brainly.com/question/14532771
#SPJ8
Solve for x, similar triangles

Answers
The value of x, considering the similar triangles, is given as follows:
x = 6.
What are similar triangles?Similar triangles are triangles that share these two features given as follows:
Congruent angle measures.Proportional side lengths.There are two similar right triangles in this problem, with equivalent sides given as follows:
5x - 3 and 39 - (5x - 3)36 and 16.Then the proportional relationship for the side lengths is given as follows:
(5x - 3)/[39 - (5x - 3)] = 36/16
Then, simplifying the denominator on the left side, we have that:
(5x - 3)/(42 - 5x) = 36/16
Applying cross multiplication, an equation is built to solve for x as follows:
36(42 - 5x) = 16(5x - 3)
1512 - 180x = 80x - 48
260x = 1560
x = 1560/260
x = 6.
More can be learned about similar triangles at brainly.com/question/14285697
#SPJ1
Please help me out :P

Answers
First one is: Linear
Second one is: f(x)=400-4x
Make me brainliest pls if I got it right :<
What are three steps of writing a number scientific notation?
Answers
Answer:
Step-by-step explanation:
Step 1: Move the decimal point to the left until you have a number greater than or equal to 1 and less than 10. Step 2: Count the number of decimal places you moved the decimal point to the left and use that number as the positive power of 10. Step 3: Multiply the decimal (in Step 1) by the power of 10 (in Step 2).
Answer:
Step 1: Move the decimal point to the left until you have a number greater than or equal to 1 and less than 10.
Step 2: Count the number of decimal places you moved the decimal point to the left and use that number as the positive power of 10.
Step 3: Multiply the decimal (in Step 1) by the power of 10
Which is a correct expansion of the following expression?
18(x – 3) – 26
A. 18x – 80
B. 18x + 80
C. 18x + 28
D. – 62x
Answers
Answer:
A. 18x – 80
Step-by-step explanation:
18(x - 3) - 26
18x - 54 - 26
18x – 80
Because first you will expand the brackets, for this you will multiply everything that is outside the bracket to what’s inside (18 times x) which will give you 18x and (18 times -3) which will give you -54
Now your equation will be
18x -54 - 26
Next you will workout the liked terms with are -54 and -26, since they are both negative just add them together and keep the sign.
To get your final answer
18x -80
425L + 125S >= 4,800
Total 15 devices
Answers
Since He Sells 15 Iteam The He Meet His Goal Of L + S >= 12
As Far As The Other Inequlty
425*9 + 125*6 = $4575 (Goal Acheived)
The Answer Is Yes He Meets Both Of His Goals
Find the coordinates of the intersection of the diagnosis of the parallelograms (-2,-1) (1,3) (6,3) and (3,-1)
Answers
Answer:
\(M = (2,1)\)
Step-by-step explanation:
Represent the diagonals as:
\(A =(-2,-1)\)
\(B =(1,3)\)
\(C =(6,3)\)
\(D = (3,-1)\)
Required
Determine the coordinate of the intersection
To do this, we simply calculate the midpoint of AC or BD.
For AC:
\((x_1,y_1) = (-2,-1)\)
\((x_2,y_2) = (6,3)\)
The midpoint is:
\(M = \frac{1}{2}\{(x_1+x_2),(y_1+y_2)\}\)
This gives:
\(M = \frac{1}{2}\{(-2+6),(-1+3)\}\)
\(M = \frac{1}{2}\{(4),(2)\}\)
\(M = (\frac{1}{2} * 4,\frac{1}{2} * 2)\)
\(M = (2,1)\)
For BD:
\((x_1,y_1) = (1,3)\)
\((x_2,y_2) = (3,-1)\)
The midpoint is:
\(M = \frac{1}{2}\{(x_1+x_2),(y_1+y_2)\}\)
This gives:
\(M = \frac{1}{2}\{(1+3),(3-1)\}\)
\(M = \frac{1}{2}\{(4),(2)\}\)
\(M = (\frac{1}{2} * 4,\frac{1}{2} * 2)\)
\(M = (2,1)\)
Notice the midpoints are the same:
\(M = (2,1)\)
Hence, the coordinates of the intersection is (2,1)
Consider the following differential equation to be solved by variation of parameters. 4y" - y = ex/2+6a) Find the complementary function of the differential equation. Y-(x) = b) Find the general solution of the differential equation. y(x) =
Answers
a) The complementary function is Y_c(x) = C1 * eˣ/₂ + C2 * e⁻ˣ/₂, where C1 and C2 are constants.
b) The general solution is y(x) = Y_c(x) + Y_p(x) = C1 * eˣ/₂ + C2 * e⁻ˣ/₂ + x * eˣ/₂ - 6x.
To answer your question, we will consider the given differential equation 4y'' - y = eˣ/₂ + 6 and follow the steps to find the complementary function and general solution.
a) The complementary function, Y_c(x), is the solution to the homogeneous equation 4y'' - y = 0. First, we find the characteristic equation: 4r² - 1 = 0. Solving for r, we get r = ±1/2.
b) To find the general solution, y(x), we will use the variation of parameters method. First, let v1(x) = eˣ/₂ and v2(x) = e⁻ˣ/₂. Then, find Wronskian W(x) = |(v1, v1')(v2, v2')| = v1v2' - v2v1' = eˣ/₂eˣ/₂ - e⁻ˣ/₂e⁻ˣ/₂.
Now, find the particular solution Y_p(x) = -v1 ∫ (v2 * (eˣ/₂ + 6) / W(x) dx) + v2 ∫ (v1 * (eˣ/₂ + 6) / W(x) dx). Solving the integrals and simplifying, we obtain Y_p(x) = x * eˣ/₂ - 6x.
To know more about differential equation click on below link:
https://brainly.com/question/14620493#
#SPJ11
if necessary, how can a student determine the change in angular momentum δlδl of the cylinder from t=0t=0 to t=t0t=t0?
Answers
To determine the change in angular momentum (ΔL) of a cylinder from t = 0 to t = t0, a student can use the equation:
ΔL = I * Δω
where ΔL is the change in angular momentum, I is the moment of inertia of the cylinder, and Δω is the change in angular velocity.
To calculate Δω, the student needs to know the initial and final angular velocities, ω0 and ωt0, respectively. The change in angular velocity can be calculated as:
Δω = ωt0 - ω0
Once Δω is determined, the student can use the moment of inertia (I) of the cylinder to calculate ΔL using the equation mentioned earlier.
The moment of inertia (I) depends on the mass distribution and shape of the cylinder. For a solid cylinder rotating about its central axis, the moment of inertia is given by:
I = (1/2) * m * r^2
where m is the mass of the cylinder and r is the radius of the cylinder.
By substituting the known values for Δω and I into the equation ΔL = I * Δω, the student can calculate the change in angular momentum (ΔL) of the cylinder from t = 0 to t = t0.
It's important to note that this method assumes that no external torques act on the cylinder during the time interval. If there are external torques involved, the equation for ΔL would need to include those torques as well.
To learn more about angular momentum click here:
brainly.com/question/31592991
#SPJ11
**15 Points**
Find the rate of change.
Graph attached
A. –7,500; The value drops $7,500 every year.
B. –750; The value drops $750 every year.
C. –75; The value drops $75 every year.
D. –1; The value drops $1 every year.

Answers
Answer:
B
Step-by-step explanation:
HELP! what is the measure of < B
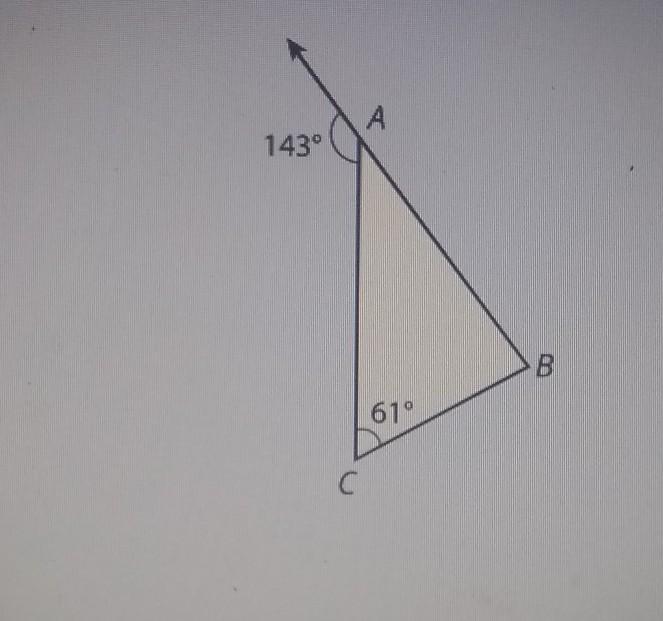
Answers
Answer:
m∠B = 98°
Step-by-step explanation:
180° - 143° = 37°
61° + 37° = 98°
m∠B = 98°