The measure of an interior angle of a regular polygon is 174. Find the number of sides in the polygon.
Answers
Answer:
60 sides
Step-by-step explanation:
The formula for the sum of the interior angles of a polygon with n sides is 180(n -2). The problem also tells you that each angle is 174, so the sum of the interior angles would also be 174n.
Then, you get the equation
180(n - 2) = 174n
180n - 360 = 174n
6n = 360
n = 60 sides.
Related Questions
Grace bought a new high-definition television and a video gaming system. The television cost $565.59 more than the video gaming system. The television cost $965.58. How could you write this equation to find the cost of the gaming system when c = the cost of the gaming system?
Answers
Answer:
565.59$ + c = $ 965.58
Step-by-step explanation:
-7 - 8s = -7s
solve for s
Answers
Answer:
s = -7
Step-by-step explanation:
isolate the variable by dividing each side by factors that don't contain the variable.
Answer: s=−7
Step-by-step explanation: if i helped plz mark as brainliest
ANSWER QUESTION 7 PLEASE

Answers
Answer:Its F
Step-by-step explanation:
Answer:
Letter i
Step-by-step explanation:
BeCuAsE A rAtIoNaL NuMbEr Is A NuMbEr ThAt CaN Be MaDe InTo A FrAcTiOn AnD I CaNt Be MaDe InTo A FrAcTiOn.
What is 40% of a circle of radius 225 feet
Answers
Answer:
About 63,617 ft²
Step-by-step explanation:
[] The area of a circle is equal to πr²
π(225)² ≈ 159,043
[] To find 40%, we can multiply our whole by 40%
-> 40% divided by 100, 0.4, becomes a decimal
159,043 * 0.4 = 63,617
-> Don't forget to add on the units once you are done, this problem was done in feet, since it is an area we used feet squared
Have a nice day!
I hope this is what you are looking for, but if not - comment! I will edit and update my answer accordingly.
- Heather
Can someone help me pls
4. Find (5.8 104) + (7.17 x 10).
Express you answer in scientific
notation. Show your work.

Answers
Step-by-step explanation:
(5.8 x 10⁴) + (7.17 × 10^6) =
(5.8 × 10⁴) + ( 717 × 10⁴)
= (5.8 +717) × 10⁴
= 722.8 × 10⁴
= 7.228 × 10^6
**WILL GIVE BRAINLIEST IF YOU EXPLAIN**
Triangles DEF and GHI are shown. Which sequence of rotations, reflections, and/or translations would map triangle DEF onto triangle GHI?
Does mapping triangle DEF onto triangle GHI prove the two triangles are congruent? Explain your reasoning.

Answers
Answer:
Part A:
The sequence of transformation that maps triangle DEF to triangle GHI are;
1) A reflection across the y-axis (x, y) →(-x, y) and
2) A translation 6 units down, (-x, y - 6)
Part B:
1) Yes
2) The points of the triangle GHI obtained from the mapping of triangle DEF using the given transformation are corresponding therefore, the mapping proves that the two triangles are congruent
Step-by-step explanation:
Part A:
The given coordinates of the vertices of triangle DEF are;
F(-1, 5), D(-5, 2), and E(-3, 1)
The given coordinates of the vertices of triangle IHG are;
I(1, -1), H(3, -5), and G(5, -4)
Therefore, the transformation that maps ΔDEF to ΔGHI are
1) A reflection across the y-axis (x, y) →(-x, y) and
2) A translation 6 units down, (-x, y - 6)
Reflection of point F(-1, 5) across the y-axis gives → (1, 5)
Followed by a translation 6 units down gives;
(1, 5) →T(y - 6) → I(1, -1)
Reflection of point D(-5, 2) across the y-axis gives → (5, 2)
Followed by a translation 6 units down gives;
(5, 2) →T(y - 6) → G(5, -4)
Reflection of point E(-3, 1) across the y-axis gives → (3, 1)
Followed by a translation 6 units down gives;
(3, 1) →T(y - 6) → H(3, -5)
Part B:
1) Yes mapping triangle DEF onto triangle GHI proves that the two triangles are congruent
2) The points of the triangle GHI obtained from the mapping of triangle DEF are the same, therefore, the mapping proves that the two triangles are congruent
Find surface area and volume
8
40
35
24

Answers
Surface area and volume are important concepts in mathematics and engineering. Surface area refers to the total area of all the faces of a three-dimensional object, while volume is the amount of space occupied by that object. In this context, we'll be discussing how to find the surface area and volume of basic shapes, such as spheres, cylinders, and cubes.
Sphere:
A sphere is a three-dimensional shape that is perfectly round and symmetrical. To find its surface area and volume, we need to know its radius (r), which is the distance from the center of the sphere to any point on its surface.
Surface Area of a Sphere = 4πr²
Volume of a Sphere = (4/3)πr³
Cylinder:
A cylinder is a three-dimensional shape with two circular faces and a curved surface that connects them. To find its surface area and volume, we need to know its radius (r) and height (h).
Surface Area of a Cylinder = 2πr² + 2πrh
Volume of a Cylinder = πr²h
Cube:
A cube is a three-dimensional shape with six square faces. To find its surface area and volume, we need to know the length of one of its sides (s).
Surface Area of a Cube = 6s²
Volume of a Cube = s³
In conclusion, Surface area is the measure of the total area that the surface of a 3D object occupies. Volume, on the other hand, is the amount of space occupied by a 3D object. To find these measurements, we use specific formulas that are unique to each 3D shape.
For more such questions on Surface area
https://brainly.com/question/16519513
#SPJ8
what is the x and y intercept of line, plz write as an ordered pair and plz give step by step explanation

Answers
Answer:
y-intercept: (0, 1)
x-intercept: (1, 0)
an x-intercept is when a line crosses the x-axis, and a y-intercept is when a line crosses the y axis.
Determine if the two triangles are congruent. If they are, state how you know.

Answers
Answer:
B) SAS
Step-by-step explanation:
The angles between the two known equal sides are called a vertical angle and are equal. Thus you know Side-Angle-Side proves congruency.
Prove that: Every sequence in R has a monotone subsequence.
Answers
By selecting a bounded subsequence from the original sequence and applying the Bolzano-Weierstrass theorem repeatedly, we can construct a monotone subsequence.
To prove that every sequence in R has a monotone subsequence, we start by considering a bounded sequence, since unbounded sequences trivially have a monotone subsequence. By applying the Bolzano-Weierstrass theorem, which guarantees that every bounded sequence in R has a convergent subsequence, we can select a subsequence that converges to a limit.
Now, let's consider this convergent subsequence. If it is already monotone, then we have found a monotone subsequence. Otherwise, we can further select a subsequence from this subsequence, applying the Bolzano-Weierstrass theorem again to find another subsequence that converges to a limit.
Repeating this process infinitely many times, we obtain a nested sequence of subsequences, each converging to a limit. By construction, each subsequence is a subset of the previous one. By the completeness of R, which ensures that every nested sequence of closed and bounded subsets in R has a non-empty intersection, we can conclude that there exists a monotone subsequence within the original sequence.
Thus, by utilizing the Bolzano-Weierstrass theorem and the completeness of R, we can establish the existence of a monotone subsequence for every sequence in R.
Learn more about sequence here:
https://brainly.com/question/30262438
#SPJ11
PLSSSS HELP I WILL GIVE BRAINLIEST
Which statements are true about the ordered pair (7, 19) and the system of equations?
{2x−y=−5x+3y=22
Select each correct answer.
The ordered pair (7, 19) is a solution to the first equation because it makes the first equation true.
The ordered pair (7, 19) is a solution to the second equation because it makes the second equation true.
The ordered pair (7, 19) is not a solution to the system because it makes at least one of the equations false.
The ordered pair (7, 19) is a solution to the system because it makes both equations true.
Answers
Answer: The ordered pair (7, 19) is not a solution to the system because it makes at least one of the equations false.
Step-by-step explanation:
In the ordered pair (7,19), 7 is the x and 19 is the y. Plug those in and multiply.
2(7)-19=-5
-5=-5
7+3(19)=22
64 doesn't =22
SO, one part of the equation is wrong making the ordered pair wrong.
What is the unknown fraction?
two tenths plus unknown fraction equals sixty seven hundredths
A twenty-seven hundredths
B forty-seven hundredths
C sixty-six hundredths
D sixty-nine hundredths
Answers
Answer:
B & 0.47
Step-by-step explanation:
0.2 + x = 0.67
reverse engineer this
0.67 - 0.2 = x
x = 0.47
0.47 = B
Answer: B.
Step-by-step explanation:
HELP PLEASE
A parking lot charges $7 per day to park on weekdays and $12 per day on weekends.
Jamal parked his car in this lot on 6 days last week and spent a total of $52. How many
weekdays and weekend days did Jamal park?
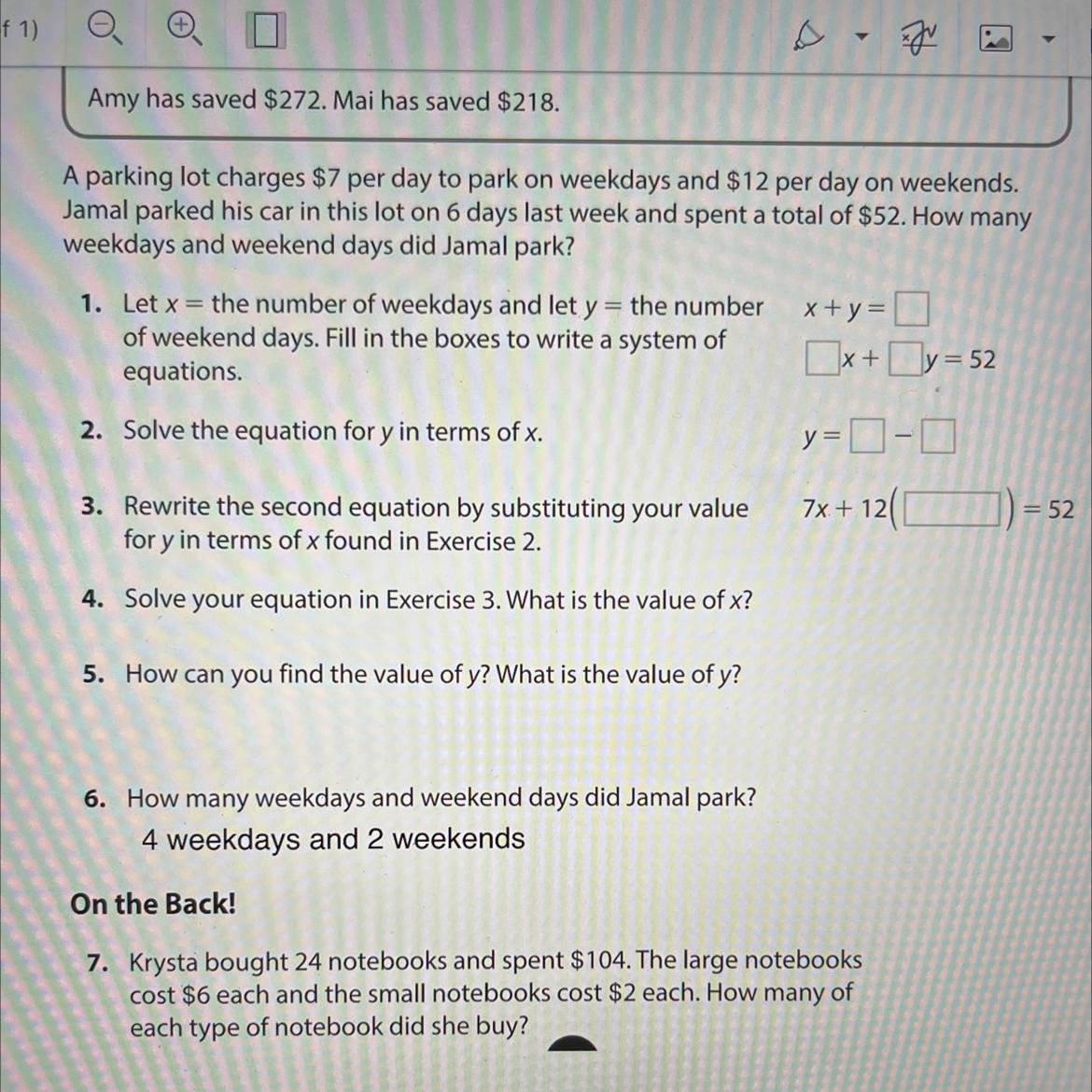
Answers
Answer:
4 weekdays and 2 weekends.
Step-by-step explanation:
6 days.
x = weekdays
y = weekends
7x = amount with weekdays
12y = amount with weekends
7x + 12y = 52, total
x + y = 6, amount of days
solve double variable equation
x = 6 - y, plug in to 1st equation
7(6 - y) + 12y = 52
42 - 7y + 12y = 52
5y = 10
y = 2 weekends
2 + x = 6
x = 4 weekdays
Over what interval is the graph of y = -(x - 5)² - 3 decreasing?
Answers
Answer: (5,♾)
Step-by-step explanation:
Anywhere after the x coordinate of the vertex
y=-(x-5)^2-3
y=-(5-5)^2-3
y=0-3
y=-3
Anywhere after (5,-3)
how many cubic millimeters are in a cubic centimeter?
Answers
1000 cubic millimeters are in a cubic centimeter.
'What is cubic centimeter?'
There are 1000 cubic millimeters in one cubic centimeter (cm³) (mm³). Add 1000 to the cubic cm number to convert it to cubic mm.
For instance, multiplying 10 by 1000 results in 10000 mm3, or how many cubic mm there are in 10 cubic cm.
The volume of small items is measured in cubic centimeters, a tiny unit of measurement. Discover standard units of measurement, the definition of cubic centimeters, how to convert them, and how to measure volume using cubic centimeters. A little cube with sides that are 1 cm long occupies the same amount of space as a cubic centimeter.
know more about standard units here
https://brainly.com/question/29439077#
#SPJ4
_____________ is multiplying the numerator of the first fraction times the denominator of the second and multiplying the denominator of the first times the numerator of the second.
Answers
Answer:
Step-by-step explanation: umm i'm a middle schooler so i tried i'm sorry.
Determine the minimum amount one will pay when making a deposit of notes and coins
Answers
To determine the minimum amount for a deposit, you need to consider the specific denominations available and the values being deposited.
The minimum amount one will pay when making a deposit of notes and coins depends on the denominations of the available notes and coins, as well as the specific amounts being deposited. To determine the minimum amount, we need to consider the smallest possible combination of notes and coins that can represent a value.
Let's assume we have the following denominations available:
Notes: $1, $5, $10, $20, $50, $100
Coins: 1 cent, 5 cents, 10 cents, 25 cents (quarters)
To find the minimum amount, we should start by using the highest denominations first and then move to lower denominations as necessary. For example, if we have to deposit $37.63, we can start by using a $20 note, then a $10 note, a $5 note, and finally two $1 notes to reach the total of $37. For the remaining 63 cents, we can use a combination of coins, such as two quarters (50 cents), one dime (10 cents), and three pennies (3 cents).
It's important to note that the specific combination of notes and coins may vary depending on the currency system and the denominations available in a particular country or region.
To determine the minimum amount for a deposit, you need to consider the specific denominations available and the values being deposited. By using the highest denominations first and then adding lower denominations as needed, you can find the minimum combination of notes and coins required to reach the deposit amount.
For more questions on amount
https://brainly.com/question/25720319
#SPJ8
what is the range of path loss exponent that will satisfy the following requirements: transmit power
Answers
The actual value of the path loss exponent will depend on various factors such as the frequency of operation, terrain, and environment.
To determine the range of path loss exponent that will satisfy the given requirements, we need to use the path loss equation, which relates the received signal power to the transmitted power, distance, and path loss exponent:
Pr = Pt - 10n log(d) - L
where Pr is the received power, Pt is the transmitted power, d is the distance between the transmitter and receiver, n is the path loss exponent, and L is the system loss.
Assuming a fixed transmit power, we can rearrange the equation to solve for the path loss exponent:
n = (Pt - Pr - L) / (10 log(d))
To satisfy the given requirements, we need to find the range of values of n such that the received power at a distance of 100 meters is at least -70 dBm.
Let's assume a system loss of 2 dB and a transmit power of 20 dBm. Then we can plug these values into the path loss equation and solve for the path loss exponent:
-70 dBm = 20 dBm - 10n log(100) - 2 dB
-48 dB = -10n log(100)
n = 2.4
Therefore, a path loss exponent between 2 and 2.4 should satisfy the given requirements. However, it's important to note that the actual value of the path loss exponent will depend on various factors such as the frequency of operation, terrain, and environment.
Learn more about environment here
https://brainly.com/question/24182291
#SPJ11
8(10-k)-2k=0 just need help solving
Answers
Answer:
k=8
Step-by-step explanation:
8(10-k)-2k=0
80-8k-2k=0
80-10k=0
-10k=-80
-80/-10
k=8
Answer:
The answer to this problem is k=8
long division synthetic division
Answers
An additional strategy for splitting polynomials is synthetic division. If you are dividing by a polynomial of degree 1, it is a shortcut for long division that only functions in that situation.
The divisor often takes the shape of (x a). Contrary to long division, you are solely concerned with the polynomials' coefficients in synthetic division.
How is lengthy synthetic division performed?Another method for dividing a polynomial by the binomial x - c, where c is a constant, is synthetic division.
Setting up the synthetic division is the first step.
Bring the leading coefficient down to the bottom row in step two.
Step 3: Divide c by the amount that was just entered in the bottom row.
Add the column you made in step 3 in step 4.
To learn more about synthetic division from given link
https://brainly.com/question/24662212
#SPJ9
(-5) -(7)=?
Helpppppp plsssss
Answers
Answer:
-12
Step-by-step explanation:
(-5)-(7) can easily be called -5-7 when all the brackets are taken away
-5-7= -12
Answer:
You can use the additive inverse to solve for x
Step-by-step explanation:
The additive inverse acquits you to change two things: the negative sign and -7
Therefore, after implementing the additive inverse, here's your expression: -5 + -7. Remeber, the rule for adding negative rational numbers: the sum of 2 negative numbers will be negative. Therefore, simply add 7 + 5 to get 12. Remebering out rule of adding negative rational numbers, you should receive -12 as your answer.
Find each percent change. Use a calculator and round answer to the nearest tenth as needed. State if it is an increase or decrease. 88 to 20.
A.22.7% decrease
B.14.2% decrease
C.77.3% decrease
D.340% decrease
Answers
well, if a value goes from 88 to 20, it clearly decreased, hmmm 88 - 20 = 68, by 68 units.
so if we take 88(origin amount) to be the 100%, what's 68 off of it in percentage?
\(\begin{array}{ccll} amount&\%\\ \cline{1-2} 88 & 100\\ 68& x \end{array} \implies \cfrac{88}{68}~~=~~\cfrac{100}{x} \\\\\\ \cfrac{ 22 }{ 17 } ~~=~~ \cfrac{ 100 }{ x }\implies 22x=1700\implies x=\cfrac{1700}{22}\implies x\approx 77.3\)
In this challenge problem set, you will investigate Kepler's laws in the special case where r(t) is a circular To complete the second challenge problem set, you will write up solutions to the following problems. Your write-up should include exposition and read like a chapter or section of a textbook. Be sure to clearly label your answers to the questions. (1) Suppose the distance between the planet and the Sun is R, and consider the circular orbit r(t) = (Rcos(ut), Rsin(t)) (a) Find constraints on w (in terms of G. M and R) so that r(t) satisfies the differential equation 1.1. (b) Use part (a) to deduce a version of Kepler's Third Law for this orbit. R³ GM (Hint: What is the relationship between and T?) r(t) = (R cos(wt), R sin(wt))
Answers
We have found a version of Kepler's Third Law for this orbit, given by R³/GM.
Given the following scenario,
The distance between the planet and the Sun is R, and consider the circular orbit r(t) = (R cos(ωt), R sin(ωt)).
The differential equation of the orbit is given by 1.1.
Determine the Kepler's laws in the special case where r(t) is a circular.
To solve the problem, we need to follow the steps below:
a. Solve for the differential equation, 1.1
b. Find constraints on ω in terms of G, M and R
c. Use part (b) to deduce a version of Kepler's Third Law for this orbit.
For part a),The differential equation of the orbit is given by;
(d²r/dt²) = -GMr/R³,where r = (R cos(ωt), R sin(ωt))
Differentiating twice w.r.t time t;
d/dt (d/dt(Rcos(ωt))) = -GM/(R²)cos(ωt)d/dt (d/dt(Rsin(ωt)))
= -GM/(R²)sin(ωt)d²(Rcos(ωt))/dt²
= -(GM/R³)(Rcos(ωt))d²(Rsin(ωt))/dt²
= -(GM/R³)(Rsin(ωt))
Therefore,
d²r/dt² = (-GM/R³)(Rcos(ωt))î + (-GM/R³)(Rsin(ωt))ĵ
= -(GM/R²)r
Similarly, we see that dr/dt = ω(-Rsin(ωt))î + ω(Rcos(ωt))ĵ.
Hence, r x dr/dt = -ωR² î + ωR² ĵ = -ωR² r_⊥, where r_⊥ is the vector perpendicular to r.
Since the orbit is circular, the acceleration is perpendicular to the velocity (i.e. tangential), so we can write
F = ma
= m(d²r/dt²)
= -GMm/R²
= mω²R, where we have used Newton's law of gravitation and the centripetal force.
Hence,
ω²R³ = GM
⇒ ω = √(GM/R³)
Therefore, we have obtained the constraint on ω in terms of G, M, and R.
For part b),
Using the result from part a) to find Kepler's Third Law, we have
T = 2π/ω
= 2π√(R³/GM)
= 2π(R/ω)³/²
= 2π(R/GM)³/² * GM
= 2πR³/GM
We have found a version of Kepler's Third Law for this orbit, given by R³/GM.
The answer is; a. ω = √(GM/R³)b. R³/GM
To know more about orbit visit:
https://brainly.com/question/32355752
#SPJ11
Simplify the expression: 4²+8÷2. (1 point)
O 12
020
08
016
Answers
16+8 ÷2
Solve
16+ 4
Solution
20
Answer:
16
Step-by-step explanation:
4^2=16
16÷2=8
8+8=16
answer= 16
What is the equation of this graph

Answers
Answer:
\(7y {}^{2} = 0\)
Answer:
the correct answer is y = -1/2x + 6
Step-by-step explanation:
Salve hy Setting up and Solving an Equation
Problem
Two planes leave San Antonio at the same time.
The northbound planc travels 70 mih faster than
the southbound plane. The planes are 1940 mi
upart in 2 h. How fast is the southbound plane
flying?

Answers
Answer:
Speed of the southbound plane = 450 mph
Step-by-step explanation:
Let the speed of the northbound plane = x miles per hour
And the speed of the southbound plane = y mph
Since, northbound plane travels 70 mph faster than the southbound plane,
x = y + 70 -----(1)
The planes are 1940 miles apart in 2 hours.
From the formula,
Distance traveled = Speed × time
Distance traveled by northbound plane in 2 hours = 2x miles
Distance traveled by the southbound plane in 2 hours = 2y miles
2x + 2y = 1940
x + y = 970 -----(2)
By substituting the value of x in equation (2) from equation (1)
y + 70 + y = 970
2y = 970 - 70
y = 450 mph
from equation (2)
x + 450 = 970
x = 520 mph
Consider the table shown above. What is the value of f(g(3)) ?

Answers
Answer: D-8
Step-by-step explanation:
6+2
The value of f(5), according to the provided table, is 5.
Evaluation of Functions:Evaluating a function means finding the value of an input inserted in a certain function. The input is the domain of the function, and the result is the range of the function. The domain is represented by the x-axis and the range is represented by the y-axis when a function is graphed.
The function f(g(x)) is called a composite function because it is made of two functions. For composite functions, the final value is obtained by performing two steps. The first step is finding the value of the function on the inside. Then, the value of the inside function is used, and the outer function is calculated for that value. So we first have to find the value of g(3), meaning that x is equal to 3.
According to the provided table for the values of x and g(x), when the value of x is 3, the value of g(x) is 6. This is the first step. The subsequent step is finding the value of the f(x) function. The x of this function is the value of g(x), which is 6. The value of f(5), according to the provided table, is 5.
Learn more about Evaluation of Functions at:
https://brainly.com/question/11270390
#SPJ2
Directions: Convert each 12-hour time to 24-hour time.
3:45 a.m. ______________
9:16 a.m. ______________
5:45 a.m. ______________
12:00 midnight ______________
12:00 noon ______________
Answers
The requreid, time in a 24-hour time clock format is given as,
3:45 a.m. -> 03:45
9:16 a.m. -> 09:16
5:45 a.m. -> 05:45
12:00 midnight -> 00:00
12:00 noon -> 12:00
There is no "a.m." or "p.m." designation in 24-hour time, and times after 12:00 are designated as 13:00, 14:00, etc. up to 23:00, after which it resets to 00:00 for midnight.
So, the given time in 24-hour clock format is given as:
3:45 a.m. -> 03:45
9:16 a.m. -> 09:16
5:45 a.m. -> 05:45
12:00 midnight -> 00:00
12:00 noon -> 12:00
Learn more about clock formats here;
https://brainly.com/question/29124204
#SPJ1
Suppose that X is a random variable with mean 20 and standard deviation 4. Also suppose that Y is a random variable with mean 40 and standard deviation 7. Find the mean and the variance of the random variable Z for each of the following cases. Be sure to show your work.
(a) Z = 40 - 5X
(b) Z = 15X - 20
(c) Z = X + Y
(d) Z = X - Y
(e) Z = -2X + 3Y
Answers
(a) The mean of Z in case (a) is -60 and the variance is 400.
(b) The mean of Z in case (b) is 280 and the variance is 3600.
(c) The mean of Z in case (c) is 60 and the variance is 65.
(d) The mean of Z in case (d) is -20 and the variance is 65.
(e) The mean of Z in case (e) is 80 and the variance is 505.
To find the mean and variance of the random variable Z for each case, we can use the properties of means and variances.
(a) Z = 40 - 5X
Mean of Z:
E(Z) = E(40 - 5X) = 40 - 5E(X) = 40 - 5 * 20 = 40 - 100 = -60
Variance of Z:
Var(Z) = Var(40 - 5X) = Var(-5X) = (-5)² * Var(X) = 25 * Var(X) = 25 * (4)² = 25 * 16 = 400
Therefore, the mean of Z in case (a) is -60 and the variance is 400.
(b) Z = 15X - 20
Mean of Z:
E(Z) = E(15X - 20) = 15E(X) - 20 = 15 * 20 - 20 = 300 - 20 = 280
Variance of Z:
Var(Z) = Var(15X - 20) = Var(15X) = (15)² * Var(X) = 225 * Var(X) = 225 * (4)² = 225 * 16 = 3600
Therefore, the mean of Z in case (b) is 280 and the variance is 3600.
(c) Z = X + Y
Mean of Z:
E(Z) = E(X + Y) = E(X) + E(Y) = 20 + 40 = 60
Variance of Z:
Var(Z) = Var(X + Y) = Var(X) + Var(Y) = (4)² + (7)² = 16 + 49 = 65
Therefore, the mean of Z in case (c) is 60 and the variance is 65.
(d) Z = X - Y
Mean of Z:
E(Z) = E(X - Y) = E(X) - E(Y) = 20 - 40 = -20
Variance of Z:
Var(Z) = Var(X - Y) = Var(X) + Var(Y) = (4)² + (7)² = 16 + 49 = 65
Therefore, the mean of Z in case (d) is -20 and the variance is 65.
(e) Z = -2X + 3Y
Mean of Z:
E(Z) = E(-2X + 3Y) = -2E(X) + 3E(Y) = -2 * 20 + 3 * 40 = -40 + 120 = 80
Variance of Z:
Var(Z) = Var(-2X + 3Y) = (-2)² * Var(X) + (3)² * Var(Y) = 4 * 16 + 9 * 49 = 64 + 441 = 505
Therefore, the mean of Z in case (e) is 80 and the variance is 505.
Learn more about Mean and Variance at
brainly.com/question/29253308
#SPJ4
Figure 1 and figure 2 are right triangles.
two right triangles labeled figure 1 and figure 2, where the legs of figure 1 are 3 units long and the legs of figure 2 are 4 units long
What scale factor was used to produce Figure 2 from Figure 1?
3
4
3 over 4
4 over 3
Answers
Answer:
4/3
Step-by-step explanation:
To find the scale factor from figure 1 to figure 2, divide a length in figure 2 by its corresponding length in figure 1.
Both legs of figure 1 measure 3 units.
Both legs of figure 2 measure 4 units.
Each leg measuring 3 units corresponds to a leg measuring 4.
scale factor = (length in figure 2)/(corresponding length in figure 1)
scale factor = 4/3
Check:
The way a scale factor works is that when you multiply a length in figure 1 by the scale factor, you get the corresponding length in figure 2.
figure 1 length: 3
scale factor: 4/3
product: 3 × 4/3 = 12/3 = 4
Yes, we do the correct length in figure 2, so our scale factor of 4/3 is correct.