The number of cubes form a pattern.
a) Draw an expression for the number of cubes in figure n.
b) How many cubes are there in the 50th figure?
c) What number has the figure consisting of 156 cubes

Answers
Answer:
in the 50th cube I think it's 250, because your just adding 5 each time, and for the cube equal to 156 that is uh I don't really know, try the 50th one, because 5x50 is 155
Step-by-step explanation:
I am so sorry if I'm wrong.
Related Questions
Find the present value of 30 annual payments of $4,500 per annum where the first payment is made 5 years from now. So there are 30 annual payments from t=5 to t=34 inclusive. The discount rate is 9% pa. The present value of these payments is: Select one: a. $49,999.998 b. $47,550.695 c. $35,421.2587 d. $33,686.1107 e. $32,751.5184
Answers
The present value of 30 annual payments of $4,500 per annum where the first payment is made 5 years from now with a discount rate of 9% per annum is $49,999.998. Therefore, the correct option is a. $49,999.998.
Present Value (PV) is the value at which the money that is expected to be received at some future time is worth in today's dollars. It is also called the "discounted value." It is used to measure the value of a future amount in today's dollars. Therefore, it is an essential component of discounted cash flow analysis, used to calculate the value of an investment or debt instrument over time.
The formula to calculate the present value of annuity formula is as follows: PV = [PMT * (1 - (1 / (1 + r)n))]/r
Where,PV = present value of annuity
PMT = payment made every year
r = rate of interest per year
n = number of years
An annuity is a fixed sum of money paid each year.
To know more about present value, visit:
https://brainly.com/question/28299316
#SPJ11
In AAEC, G is the centroid.
A
B.
If EG = 6, find GB.
O 2
03
06
09
Answers
B) The length of GB is 3 in the given triangle.
The centroid of a triangle is the point at which the three medians of the triangle intersect. A median of a triangle is a line segment that connects a vertex of the triangle to the midpoint of the opposite side. The three medians divide the triangle into six smaller triangles, each with a vertex at the centroid.
The ratio in which the centroid divides a median of a triangle is 2:1. That is, the distance from the centroid to the vertex is twice the distance from the centroid to the midpoint of the opposite side.
So, if G is the centroid and B is the midpoint of the side opposite to point A, the ratio of EG: GB is 2:1.
so the length of GB = EG/2
so the length of GB = 3
To know more about median click on below link:
https://brainly.com/question/28060453#
#SPJ4
Complete question:
In ΔAEC, G is the centroid , as shown in the figure .
if EG = 6 ,find GB
A) 2
B) 3
C) 6
D) 9

Find a function r(t) that describes the line segment from P(2,7,3) to Q(3,1,1). A. r(t)=⟨2−t,7+6t,3+2t⟩;0≤t≤1 B. r(t)=⟨2+t,7−6t,3−2t⟩;0≤t≤1 C. r(t)=⟨2+t,7−6t,3−2t⟩;1≤t≤2 D. r(t)=⟨2−t,7+6t,3+2t⟩;1≤t≤2
Answers
The correct function that describes the line segment from P(2,7,3) to Q(3,1,1) is r(t) = ⟨2 + t, 7 - 6t, 3 - 2t⟩; 0 ≤ t ≤ 1.
The function that describes the line segment from point P(2,7,3) to Q(3,1,1), we can use the parametric form of a line. The general form of a line equation is r(t) = ⟨x₀ + at, y₀ + bt, z₀ + ct⟩, where (x₀, y₀, z₀) is a point on the line and (a, b, c) are direction ratios.
1. First, we find the direction ratios by subtracting the coordinates of P from Q:
a = 3 - 2 = 1
b = 1 - 7 = -6
c = 1 - 3 = -2
2. Next, we substitute the point P(2,7,3) into the line equation and simplify:
r(t) = ⟨2 + t, 7 - 6t, 3 - 2t⟩
3. The parameter t represents the distance along the line segment. Since we want to describe the segment from P to Q, we need t to vary from 0 to 1, ensuring that we cover the entire segment.
4. Comparing the obtained equation with the given options, we find that the correct function is r(t) = ⟨2 + t, 7 - 6t, 3 - 2t⟩; 0 ≤ t ≤ 1.
Therefore, option A, r(t) = ⟨2 - t, 7 + 6t, 3 + 2t⟩; 0 ≤ t ≤ 1, is the correct answer.
Learn more about function : brainly.com/question/28278690
#SPJ11
There are four candidates for homecoming queen and three candidates for king. How many king-queen pairs are possible?
Answers
The number of possible king-queen pairs can be determined by multiplying the number of candidates for king by the number of candidates for queen.
To calculate the number of king-queen pairs, we multiply the number of candidates for king by the number of candidates for queen. In this case, there are four candidates for homecoming queen and three candidates for king. Therefore, the total number of king-queen pairs would be 4 multiplied by 3, which equals 12.
Each candidate for king can be paired with each candidate for queen, resulting in multiple possible combinations. By multiplying the number of candidates for each position, we account for all possible pairings. In this scenario, there are three potential kings and four potential queens. For each king, there are four possible queens he can be paired with. Since there are three kings, we multiply 3 by 4 to get the total number of 12 king-queen pairs.
Learn more about multiply here: https://brainly.com/question/30875464
#SPJ11
Find the volume of the composite solid. Round your answer to the nearest hundredth.

Answers
The volume of the composite solid is 310.86 cubic centimeter where it has a cylinder and cone.
The composite figure has a cylinder and cone
The volume of cylinder =πr²h
The radius of cylinder is 3 cm and height is 10 cm
Volume of cylinder = 3.14×3²×10
=3.14×9×10
=282.6 cubic centimeter
Now let us find volume of cone
Volume of cone = πr²h/3
Radius of cone is 3 cm and height is 3 cm
Volume of cone = 3.14×9×3/3
=28.26cubic centimeter
Total volume = 282.6 + 28.26
=310.86 cubic centimeter
To learn more on Three dimensional figure click:
https://brainly.com/question/2400003
#SPJ1
A student has some $1 and $5 bills in his wallet. He has a total of 19 bills and that are worth $55. how many of each type of bill does he have
Answers
Answer:
y= 9 ( 5 dollars bill)
x=10 ( one dollar bill)
Step-by-step explanation:
let x be the one dollar bill and y the 5 dollar bill
x+y=19 ⇒ x=19-y
x+5y=55 ( solve by substitute x=19-y)
19-y+5y=55
4y=55-19
4y=36 ⇒ y=36/4
y= 9 ( 5 dollars bill)
x+y=19
x+9=19
x=19-9
x=10 ( one dollar bill)
check :
x+5y=55
10+5(9)=
10+45 = 55 dollars
100 POINTS + BRAINLEIST ANSWER ASAP

Answers
Answer:
BC = 60
Step-by-step explanation:
We can model the line with the expression
AB + BC = AC Sub each equation
8x + 9 + 6x + 6 = 141 Combine like terms
14x + 15 = 141 Subtract 15
14x = 126 Divide by 14
x = 9
Now we can use x to find BC
BC = 6x + 6
BC = 6(9) + 6
BC = 54 + 6
BC = 60
If your insurance has a $2,500 deductible, and 20% coinsurance for hospitalizations, and a $5,200 out of pocket maximum, how much of a $12,500 hospitalization would you pay? $4,500 $2,500 $5,000 $2,500 $5,200
Answers
Based on the given insurance plan, if you have a $12,500 hospitalization, you would pay $2,500.
You would pay $2,500.
The $2,500 is equal to the deductible amount specified in the insurance plan. A deductible is the initial amount you need to pay out of pocket before your insurance coverage kicks in. In this case, the deductible is $2,500, so you are responsible for paying that amount.
The $2,500 is the total amount you would pay for the hospitalization. It represents the deductible portion, which you need to cover before the insurance starts sharing the costs with you. After you meet the deductible, the coinsurance comes into effect. The 20% coinsurance means that you would be responsible for paying 20% of the remaining expenses, while the insurance would cover the remaining 80%. However, since the out-of-pocket maximum is $5,200, and your hospitalization cost is $12,500, you would not reach the out-of-pocket maximum in this case. Therefore, you would pay the deductible amount of $2,500.
Learn more about hospitalization
brainly.com/question/28781701
#SPJ11
Suppose the number of flaws in a thin copper wire follows a Poisson distribution with = 2.3 flaws per millimeter. (a) Determine the probability of exactly 2 flaws in 1 millimeter of wire. (Give your answer to four decimal places) (b) Determine the probability of at most 2 flaws in 5 millimeters of wire. (Give your answer to four decimal places) 3. Let X be a random variable with the following cumulative distrib=ution function. F(x) = c (8x* – 3x), 0
Answers
a) The probability of exactly 2 flaws in 1 millimeter of wire is approximately 0.2645.
b) There is no positive constant c that satisfies all the properties of a cumulative distribution function.
(a) The probability of exactly 2 flaws in 1 millimeter of wire is given by the Poisson probability mass function:
P(X = 2) = (e^(-λ) * λ^x) / x!
where λ = 2.3 and x = 2.
Substituting these values, we get:
P(X = 2) = (e^(-2.3) * 2.3^2) / 2! = 0.2645 (rounded to four decimal places)
Therefore, the probability of exactly 2 flaws in 1 millimeter of wire is approximately 0.2645.
(b) The probability of at most 2 flaws in 5 millimeters of wire is given by the cumulative distribution function of a Poisson distribution with mean λ = 5*2.3 = 11.5:
P(X ≤ 2) = P(X = 0) + P(X = 1) + P(X = 2)
= (e^(-11.5) * 11.5^0) / 0! + (e^(-11.5) * 11.5^1) / 1! + (e^(-11.5) * 11.5^2) / 2!
= 0.0086 + 0.0495 + 0.1420
= 0.2001 (rounded to four decimal places)
Therefore, the probability of at most 2 flaws in 5 millimeters of wire is approximately 0.2001.
(c) The cumulative distribution function F(x) is given by:
F(x) = c(8x^2 – 3x), 0 <= x <= 2
Since F(x) is a cumulative distribution function, it satisfies the following properties:
F(x) is non-negative for all x
F(x) is non-decreasing as x increases
Lim x->-∞ F(x) = 0 and Lim x->+∞ F(x) = 1
Using these properties, we can solve for the constant c:
Lim x->-∞ F(x) = 0 => c(8*(-∞)^2 – 3*(-∞)) = 0 => c = 0
Lim x->+∞ F(x) = 1 => c(8*(+∞)^2 – 3*(+∞)) = 1 => c = 0 (since 8*(+∞)^2 is much larger than 3*(+∞))
Therefore, there is no positive constant c that satisfies all the properties of a cumulative distribution function.
Hence, the given function cannot be a cumulative distribution function.
Learn more about probability here:
https://brainly.com/question/32117953
#SPJ11
The function f(x) = -2-^3 + 5x^2 - 3x + 1 is
A. Neither even or odd
B. Odd
C. Even
D. Symmetric about the y-axis
Answers
Analyzing the function f(x) = -2•x³ + 5•x² - 3•x + 1, using the criteria f(x) = f(-x) for even functions and f(x) = -f(-x) for odd functions, gives the correct option as the option
A. Neither even or odd
What are the the differences between even and odd functions?An even function satisfy the equation f(x) = f(-x)
An even function is one that is symmetrical about the y-axis
An odd function satisfy the equation f(x) = -f(-x)
The shape graph of an odd function is inverted as it crosses the y-axis.
Analyzing the function f(x) = -2•x³ + 5•x² - 3•x + 1 gives;
f(1) = -2•1³ + 5•1² - 3•1 + 1 = -1
f(-1) = -2•(-1)³ + 5•(-1)² - 3•(-1) + 1 = 11
f(1) ≠ f(-1)
-f(-1) = -2•(-1)³ + 5•(-1)² - 3•(-1) + 1 = 11
f(1) ≠ -f(-1)
The function is therefore;
A. Neither even or oddLearn more about the graphs of functions here:
https://brainly.com/question/17089414
#SPJ1
Expand the given logarithm and simplify. Assume when necessary that all quantities represent positive real numbers. Be sure to factor out any common factors in your final answer.
log5(125/ x^{2}-576)
Answers
Answer:
ok you deleted my other answer
Step-by-step explanation:
im just finishing this challenge and you are the last question i need to answer
Evaluate the function for (a) x = -2, (b) x = 0, and (c) x = 2.
h(x) = 5x-x^2

Answers
We evaluated the function and we got
\(h(-2)=-14\\h(0)=0\\h(2)=6\)
Let us evaluate that function for \(x = -2\)
We can substitute the value of \(x\) in the given expression
\(h(-2)=5(-2)-(-2)^{2}\)
\(=-10-4\\=-14\)
\(h(-2)=-14\)
Now, we can evaluate the function for \(x=0\)
Let's substitute the value of \(x\) in the given expression
\(h(0)=5(0)-0^{2} \\h(0)=0\)
Now, we can evaluate the function for \(x=2\)
Let's substitute the value of \(x\) in the given expression
\(h(2)=5(2)-2^{2} \\h(2)=10-4\\h(2)=6\)
Hence, we evaluate the function
\(h(-2)=-14\\h(0)=0\\h(2)=6\)
To know more,
brainly.in/question/10703570
Effective situational leaders demonstrate a high degree of ______. Honesty extraversion empathy flexibility g
Answers
Effective situational leaders demonstrate a high degree of flexibility.
What is Flexibility ?Flexibility is a key quality for situational leaders since they must modify their style of leadership according to the circumstances, the demands of their team, and the objectives to be met. They are able to modify their strategy, communication style, and decision-making process to suit the demands of various situations.
Flexibility stands out as a crucial feature that enables leaders to negotiate a variety of situations and guide their teams to success, even though honesty, extraversion, empathy, and other qualities are also important in leadership.
Learn more about Flexibility here : brainly.com/question/30302105
#SPJ4
Simplify the expression. Write your answer as a power.
\((5^{4} )^{3}\)
Answers
Answer:
\(5^{12}\)
Step-by-step explanation:
Lets say there's a number 'x' and there's an expression \((x^a)^b\) where 'a' & 'b' are also numbers , the simplified form of the expression is \(x^{a \times b}\).
So ,
\((5^4)^3 = 5^{4 \times 3} = 5^{12}\)
The normal body temperature of an alien creature is 102.6ºF. The alien is considered to be in an unhealthy state if its temperature is at least 2.4ºF off from normal.
What absolute value inequality can be written to determine the range of acceptable alien body temperatures, and what is this range of temperatures?
Enter your answers in decimal form by filling in the boxes.
Absolute value inequality: $$x−≥
An alien is unhealthy if its body temperature is less than ºF or more than ºF.
Answers
Answer:
the inequality would look like this
|x-102.6| _>_2.4
An alien is unhealthy if its body temperature is less than 100.2ºF or more than 105ºF.
Determine if this is a function or not based on the graph
O yes
O no
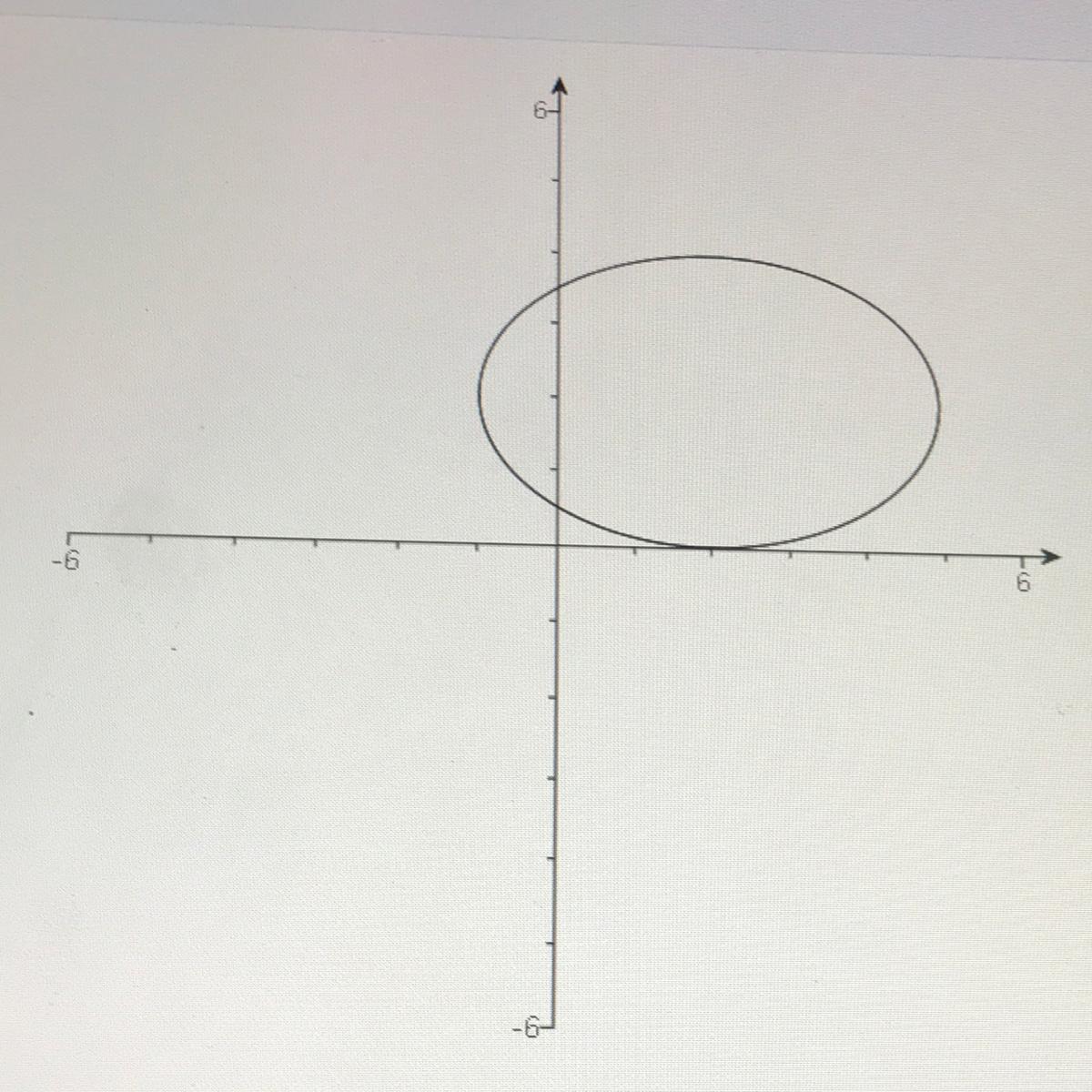
Answers
Answer:
yes
Step-by-step explanation:
brainiest plz
biden 2020 the vote is 238 {blue} and the orange is 218 cmon
Answers
Answer: Biden 2020
Step-by-step explanation:
What’s the identity property of addition?
Answers
Answer:
Identity property of addition: The sum of 0 and any number is that number. For example, 0 + 4 = 4 0 + 4 = 4 0+4=40, plus, 4, equals, 4.
Step-by-step explanation:
When csc(0)sin(0) is simplified, what is the result?
Answers
Answer:
csc θ * sin θ
Simplified using trig identities:
csc (x) = 1/sin(x)
so, csc (0) = 1/sin(0)
1/sin(0) * sin (0), the result will be sin(0) / sin (0) which is equal to 1.
Therefore, the answer is 1.
Step-by-step explanation:
Expression in sin θ and cos θ below
4cos ec^2 2θ as 2 / 2 (4 sin θ cos θ )^2
or
cos ec^2 θ as 1 / sin ^2 θ
. Accept terms like
cos ec^2 θ = 1 +cot^2 θ =1 + cot^2 θ /sin^2 θ
the weights of oranges growing in an orchard are normally distributed with a mean weight of 8 oz. and a standard deviation of 2 oz. from a batch of 1400 oranges, how many would be expected to weigh more than 4 oz. to the nearest whole number? 1) 970 2) 32 3) 1368 4) 1295
Answers
The number of oranges that are expected to weigh more than 4 oz is:
1400 - (1400 × 0.0228)≈ 1368.
The mean weight of the oranges growing in an orchard is 8 oz and standard deviation is 2 oz, the distribution of the weight of oranges can be represented as normal distribution.
From the batch of 1400 oranges, the number of oranges is expected to weigh more than 4 oz can be found using the formula for the Z-score of a given data point.
\(z = (x - μ) / σ\)
Wherez is the Z-score of the given data point x is the data point
μ is the mean weight of the oranges
σ is the standard deviation
Now, let's plug in the given values.
\(z = (4 - 8) / 2= -2\)
The area under the standard normal distribution curve to the left of a Z-score of -2 can be found using the standard normal distribution table. It is 0.0228. This means that 0.0228 of the oranges in the batch are expected to weigh less than 4 oz.
To know more about normal distribution visit :
https://brainly.com/question/23418254
#SPJ11
735+427+527+4777-526+526 times 7 plz it’s due at 1:00
Answers
Answer:
45262
Step-by-step explanation:
Answer: 45,262
Step-by-step explanation:
The area of a trapezoid is represented by the expression 12x2 + 7x – 10. The other dimensions are shown in the diagram below. Determine an expression for the height of the trapezoid.

Answers
Answer:
(24x^2 + 14x – 20) /(3x+5) = h
Step-by-step explanation:
The area of a trapezoid is given by
A =1/2 (b1+b2) h
12x^2 + 7x – 10 = 1/2 ( x+3+ 3x+2)h
Multiply each side by 2
24x^2 + 14x – 20 = ( x+3+ 3x+2)h
Combine like terms
24x^2 + 14x – 20 = ( 4x+5)h
Divide each side by (4x+5)
(24x^2 + 14x – 20) /(4x+5) = ( 4x+5)h/(4x+5)
(24x^2 + 14x – 20) /(4x+5) = h
suppose the real risk-free rate is 2.50% and the future rate of inflation is expected to be constant at 2.80%. what rate of return would you expect on a 5-year treasury security, assuming the pure expectations theory is valid? disregard cross-product terms, i.e., if averaging is required, use the arithmetic average.
Answers
5.30 % rate of return would you expect on a 5-year treasury security, assuming the pure expectations theory is valid.
Real and nominal interest rates: what are they?To reflect the true cost and purchasing power of money that is borrowed or invested, an interest rate is called a real interest rate that has been adjusted for inflation. The nominal interest rate depicts the cost of money and reflects the state of the market. A good's nominal value is its price in terms of money. Its value in relation to another good, service, or collection of goods is what determines its true worth. Given that it is the current interest rate in the economy, it is frequently referred to as the market interest rate (usually charged by banks and other institutions). Depending on the bank or the type of loans or deposits, this nominal interest rate may be 8%, 10%, or 12%.
Nominal interest rate = Real interest rate + Inflation rate
= 2.5% + 2.8%
= 5.30%
Learn more about the Nominal interest rate here: https://brainly.com/question/25877453
#SPJ1
Use propositional logic to prove that the argument is valid. Do not use truth tables (A + B) ^ (C V -B) ^(-D-->C) ^ A D Please use the following substitute operators during your quiz: ^: &
v: I
¬: !
-->: ->
Answers
To prove that the argument is valid using propositional logic, we can apply logical rules and deductions. Let's break down the argument step by step:
(A + B) ^ (C V -B) ^ (-D --> C) ^ A ^ D
We will represent the proposition as follows:
P: (A + B)
Q: (C V -B)
R: (-D --> C)
S: A
T: D
From the given premises, we can deduce the following:
P ^ Q (Conjunction Elimination)
P (Simplification)
Now, let's apply the rules of disjunction elimination:
P (S)
A + B (Simplification)
Next, let's apply the rule of disjunction introduction:
C V -B (S ^ Q)
Using disjunction elimination again, we have:
C (S ^ Q ^ R)
Finally, let's apply the rule of modus ponens:
-D (S ^ Q ^ R)
C (S ^ Q ^ R)
Since we have derived the conclusion C using valid logical rules and deductions, we can conclude that the argument is valid.
To learn more about Simplification : brainly.com/question/28261894
#SPJ11
francisco purchased a house that was worth $198,000. the value of the house increased by 6% each year for the next 5 years. the value of the house at any given moment (during the first five years) is what percent of the value of the house exactly one year earlier?
Answers
Answer:
After the first year, the value of the house would increase by 6% and become:
$198,000 + (6%/100) x $198,000 = $210,000
Similarly, after the second year, the value of the house would increase by 6% and become:
$210,000 + (6%/100) x $210,000 = $222,600
We can repeat this process for all five years to determine the final value of the house after 5 years:
$198,000 x (1 + 6%/100)^5 = $267,015.23
To find the value of the house as a percentage of the value exactly one year earlier, we can compare the value after 5 years with the value after 4 years:
$222,600/$210,000 = 1.0571
This means that the value of the house after 5 years is approximately 105.71% of the value exactly one year earlier, which is an increase of 5.71%.
Please, help me out <3

Answers
Answer:
D
Step-by-step explanation:
Every input can only have one output for it to be considered a function. There are repeats of x values with different y values in all of these except for D so D is the correct answer.
Determine if this relationship is proportional or non proportional. Explain.

Answers
The equation for the materials quantity variance is
(AQ × AP) – (SQ × SP).
(AQ × AP) – (AQ × SP).
(AQ × SP) – (SQ × SP).
(SQ × AP) – (SQ × SP).
Answers
The equation for the materials quantity variance is (AQ × AP) – (SQ × SP).
The materials quantity variance is a measure of the difference between the actual quantity (AQ) of materials used and the standard quantity (SQ) of materials that should have been used, multiplied by the standard price (SP) per unit. The variance indicates whether more or fewer materials were used compared to the standard, and it quantifies the cost impact of the difference.
The formula (AQ × AP) – (SQ × SP) calculates the materials quantity variance by multiplying the actual quantity (AQ) by the actual price (AP) per unit and subtracting the product of the standard quantity (SQ) and the standard price (SP) per unit. This formula directly compares the actual and standard quantities and calculates the cost impact of any deviations.
Therefore, the correct equation for the materials quantity variance is (AQ × AP) – (SQ × SP).
To know more about materials quantity variance click here:
we desire the residuals in our model to have which probability distribution? select answer from the options below normal binomial poisson
Answers
The distribution that the residuals in our model to follow is equals to the normal probability distribution. So, option(a).
Because residuals are defined as the difference between any data point and the regression line, they are sometimes called "errors". An error in this context does not mean that there is anything wrong with the analysis. In other words, the residual is the error that is not described by the regression line. The residue(s) can also be expressed by "e". The formula is written as, Residual = Observed value – predicted value or
\(e = y – \hat y \).
In order to draw valid conclusions from your regression, the regression residuals should follow a normal distribution. The residuals are simply the error terms or differences between the observed value of the dependent variable and the predicted value. Therefore, the residuals should have a normal distribution.
For more information about residuals, visit:
https://brainly.com/question/15404560
#SPJ4
Complete question:
we desire the residuals in our model to have which probability distribution? select answer from the options below
a) normal
b) binomial
c) poisson
solve w/ work shown please!!!

Answers
Answer:
70°
Step-by-step explanation:
This triangle is an isosceles triangle because two sides are marked that they are the same. So the "base angles" are also the same. Angle D and Angle F are equal to each other (the angles are congruent and the measures are equal).
All the angles in a triangle add up to 180° We know the one marked angle is 40°. Let Angle D be x and so Angle F is also x.
x + x + 40 = 180
combine like terms
2x + 40 = 180
subtract 40
2x = 140
divide by 2
x = 70
Angle D is 70°