The number of hours per week that the television is turned on is determined for each family in a sample. The mean of the data is 30 hours and the median is 26.2 hours. Twenty-four of the families in the sample turned on the television for 15 hours or less for the week. The 11th percentile of the data is 15 hours. Step 4 of 5 : What is the value of the 50th percentile?
Answers
Answer:
26.2 hours
Step-by-step explanation:
From the given information:
The objective is to determine the value of the 50th percentile.
The median is the 50th percentile, which categorically divides the data into two equal parts. It is a number separating the higher half of a data sample from the lower half. This implies that the median stands in place for the 50th percentile of the data.
Thus, the 50th percentile value is 26.2 hours
Related Questions
Can some please help me with this questions

Answers
9514 1404 393
Answer:
y = 100,000(1 + 0.15)^t y = 1200(1 -0.06)^t y = 49.50(1 -0.07)^t y = 135(1 +0.05)^t value of $200 decreases (decays) by 25% each yearStep-by-step explanation:
It should be no stretch to understand that "increases" means the function is a growth function (+ sign), and "decreases" means the function is a decay function (- sign).
The multiplier in front (a) is the initial value — the value when t=0.
What is 1500(0.04)(3)?
Answers
Answer:
180
Step-by-step explanation:
Answer:
180
Step-by-step explanation:
1500(0.04)(3)
in any calcoulater you will get the awnser
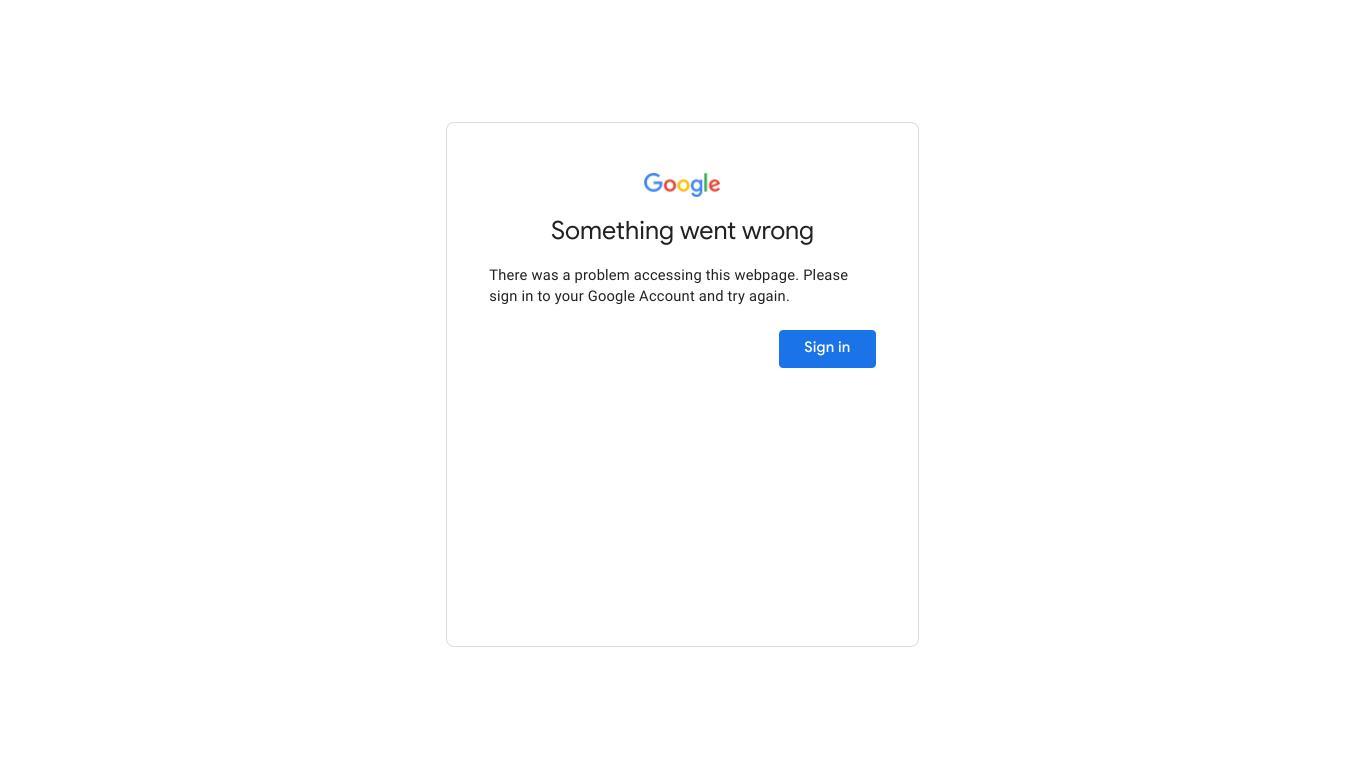
Can I get some help? Maybe from a fellow student or teacher that knows how to help with Clever? For some reason, whenever I'm trying to get into Clever, I press the login button but it takes me to this page saying something went wrong and when I click Sign In (Second picture) it stays on that page. This happened on Wednesday too, and by the time I had the email to send to my Teacher, I was able to get back in. (That time it had taken me a whole hour) I've also already tried restarting my computer too.
I'LL GLADLY GIVE BRAINLIEST TO THE PERSON WHO CAN HELP ME
Answers
Answer:
honestly, this happened to me so i clear my cache and cookies and deleted my search history and it worked
to clear cache and cookies (for chrome) go to the top right of your bookmarks bar.
there will be three tiny dots going vertical(up and down)
click on it
there will be a dropdown menu
the third to the bottom will say settings
click that
then when you are i settings, click on advanced dropdown menu(it will be on the left hand side of the screen towards the bottom)
press restore settings to their original defaults
all your cookies and cache will be deleted
your extensions will be deactivated(but not deleted dont worry)
restart your computer and then go to your history and delete everything
restart chrome and you shoul be good
Brainliest?Can someone please HELLLPPPPPPPP!!!!!!!!! Consider the set {2, 1, 3, 4}. How many proper subsets could be formed from this set?
Answers
pls help it's due for a grade

Answers
NEED HELP ASAP WILL GIVE BRAINLY IF CORRECT
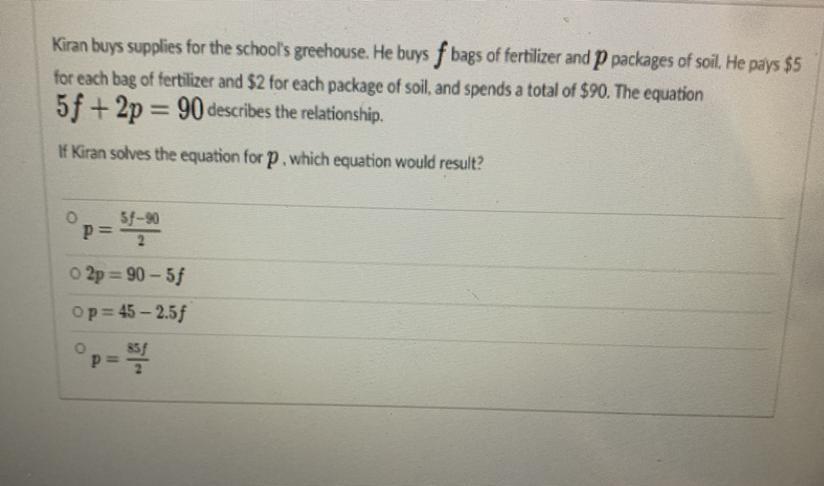
Answers
Answer:
p = 45 - 2.5f
Step-by-step explanation:
5f + 2p = 90
just manipulate the equation, treat it like a regular algebra equation and solve for p by inverse operations and simplifying
5f + 2p = 90
-5f -5f
2p = 90 - 5f
/2 /2
p = \(\frac{90 -5f}{2}\)
p = 45 - 2.5f
How i can write that numbers in letters/ como los escriboo en letras
693,5699=
34,02289=
0,789=
5691,78=
Answers
Three hundred fourty thousand two thousand and eighty nine
I’m confused on the comma for the last 2?
PLS ANSWER QUICKLY What is the best approximation of the solution to the system to the nearest integer values? (7, 0) (0, 6) (7, 1) (1, 7)
Answers
Answer:
0 = 0 = 0 = 0 = 0 < 1 < 6 < 7
0 is equal to 0 is equal to 0 is equal to 0 is equal to 0 is less than 1 is less than 6 is less than 7
0/
1
= 0/
1
= 0/
1
= 0/
1
= 0/
1
< 1/
1
< 6/
1
< 7/
1
Step-by-step explanation:
Answer:
the correct answer is (1, 7)
Step-by-step explanation:
Simplify: \(\sqrt[3]{135}\)
Answers
![Simplify: [tex]\sqrt[3]{135}[/tex]](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/GFfUm9Q98hwdJ2fVQ4JMC8eb7Xa2FgVA.png)
trucks in a delivery fleet travel a mean of 90 miles per day with a standard deviation of 18 miles per day. the mileage per day is distributed normally. find the probability that a truck drives between 122 and 127 miles in a day. round your answer to four decimal places.
Answers
The probability that a truck drives between 122 and 127 miles in a day is 0.0165, rounded to four decimal places.
To find the probability that a truck drives between 122 and 127 miles in a day, we'll use the z-score formula and standard normal distribution table. Follow these steps:
Step 1: Calculate the z-scores for 122 and 127 miles.
z = (X - μ) / σ
For 122 miles:
z1 = (122 - 90) / 18
z1 = 32 / 18
z1 ≈ 1.78
For 127 miles:
z2 = (127 - 90) / 18
z2 = 37 / 18
z2 ≈ 2.06
Step 2: Use the standard normal distribution table to find the probabilities for z1 and z2.
P(z1) ≈ 0.9625
P(z2) ≈ 0.9803
Step 3: Calculate the probability of a truck driving between 122 and 127 miles.
P(122 ≤ X ≤ 127) = P(z2) - P(z1)
P(122 ≤ X ≤ 127) = 0.9803 - 0.9625
P(122 ≤ X ≤ 127) ≈ 0.0178
So, the probability that a truck drives between 122 and 127 miles in a day is approximately 0.0178 or 1.78%.
to learn more about probability click here:
https://brainly.com/question/13604758
#SPJ11
Find the volume of the composite solid. Round your answer to the nearest hundredth. 5.1m, 5.1m, 5.1m. GIVE BRAINLIEST TO WHOEVER ANSWERS
Answers
The volume of the composite solid is 132.65 \(m^3\)
A composite solid's volume is the total amount of space it takes up. It is computed either by disassembling it into simpler shapes or by adding up the volume of each of its constituent parts. Adding or subtracting volumes of various geometric shapes may be part of the calculation process, which depends on the solid's specific composition.
Each component's volume can be calculated using the volume formulas for simple shapes like cubes, spheres, cylinders, and cones, and the overall volume of the composite solid can then be calculated.
To find the volume of the composite solid:
1. Identify the shape of the solid: Since all three dimensions (5.1m, 5.1m, and 5.1m) are equal, this is a cube.
2. Calculate the volume: The formula for the volume of a cube is V = \(side^3\)3, where "side" is the length of one side.
3. Plug in the dimensions: V = \((5.1m)^3\)= 5.1m * 5.1m * 5.1m =\(132.651m^3\).
4. Round to the nearest hundredth: The volume rounded to the nearest hundredth is \(132.65 m^3\).
So, the volume of the composite solid is \(132.65 m^3\).
Learn more about volume here:
https://brainly.com/question/23755595
#SPJ11
Solve each inequality. Check your solution. (x/3) + 5 ≥ 1/6
Answers
The inequality given by (x/3) + 5 ≥ 1/6 has the solution x ≥ -29/2 or [-29/2 , +∞).
Inequality refers to the relationship between two non-equal expressions. It can be denoted by > for greater than, < for less than, >/= for greater than and equal to, and </= for less than and equal to.
To solve an inequality is to find the values of x such that when we substitute that number for x we have a true statement.
Given the inequality (x/3) + 5 ≥ 1/6, subtract 5 from both sides.
(x/3) + 5 - 5 ≥ 1/6 - 5
x/3 ≥ -29/6
Multiply both sides by 3.
3(x/3) ≥ 3(-29/6)
x ≥ -29/2
To check, let x = -29/2
x = -29/2 ≥ -29/2
Substitute this value to the inequality.
(x/3) + 5 ≥ 1/6
(-29/2)/3 + 5 ≥ 1/6
1/6 ≥ 1/6
let x = -14,
x = -14 ≥ -29/2
Substitute this value to the inequality.
(x/3) + 5 ≥ 1/6
-14/3 + 5 ≥ 1/6
1/3 ≥ 1/6
Learn more about inequalities here: brainly.com/question/24372553
#SPJ4
A box is to be made out of a 10 cm by 20 cm piece of cardboard. Squares of side length cm will be cut out of each corner, and then the ends and sides will be folded up to form a box with an open top. (a) Express the volume V of the box as a function of x. V = cm^3 (b) Give the domain of V in interval notation. (Use the fact that length and volume must be positive.) = ? (c) Find the length L , width W, and height H of the resulting box that maximizes the volume. (Assume that W < or = to L ) L= ?cm W= ?cm H= ? cm (d) The maximum volume of the box is ? cm^3.
Answers
(a) The volume V of the box as a function of x is V = 4x^3-60x^2+200x
(b) The domain of V in interval notation is 0<x<5,
(c) The length L , width W, and height H of the resulting box that maximizes the volume is H = 2.113, W = 5.773, L= 15.773
(d) The maximum volume of the box is 192.421 cm^2.
In the given question,
A box is to be made out of a 10 cm by 20 cm piece of cardboard. Squares of side length cm will be cut out of each corner, and then the ends and sides will be folded up to form a box with an open top.
(a) We have to express the volume V of the box as a function of x.
If we cut out the squares, we'll have a length and width of 10-2x, 20-2x respectively and height of x.
So V = x(10-2x) (20-2x)
V = x(10(20-2x)-2x(20-2x))
V = x(200-20x-40x+4x^2)
V = x ( 200 - 60 x + 4x^2)
V = 4x^3-60x^2+200x
(b) Now we have to give the domain of V in interval notation.
Since the lengths must all be positive,
10-2x > 0 ≥ x < 5 and x> 0
So 0 < x < 5
(c) Now we have to find the length L , width W, and height H of the resulting box that maximizes the volume.
We take the derivative of V:
V'(x) = 12x^2-120x+200
Taking V'(x)=0
0 = 4 (3x^2-30x+50)
3x^2-30x+50=0
Now using the quadratic formula:
x=\(\frac{-b\pm\sqrt{b^2-4ac}}{2a}\)
From the equationl a=3, b=-30, c=50
Putting the value
x=\(\frac{30\pm\sqrt{(-30)^2-4\times3\times50}}{2\times3}\)
x= \(\frac{30\pm\sqrt{900-600}}{6}\)
x= \(\frac{30\pm\sqrt{300}}{6}\)
x= \(\frac{30\pm17.321}{6}\)
Since x<5,
So x= \(\frac{30-17.321}{6}\)
x= 2.113
So H = 2.113, W = 5.773, L= 15.773.
d) Now we have to find the maximum volume of the box.
V = HWL
V= 2.113*5.773*15.773
V = 192.421 cm^3
To learn more about volume of rectangle link is here
brainly.com/question/13798973
#SPJ4
Finding perimeter and area
Answers
Answer: The perimeter of a two-dimensional shape is the distance around the shape. It is found by adding up all the sides (as long as they are all the same unit). The area of a two-dimensional shape is found by counting the number of squares that cover the shape.
Step-by-step explanation:
Consider the following NLP: min s.t. 2x12+2x1x2+x22−10x1−10x2
x12+x22≤5
3x1+x2≤6
x1,x2≥0 (a) Aside from regularity and the given constraints, what are the first order necessary conditions for this problem? (Be as specific as possible.) (b) Find a solution by assuming the first Lagrangian multiplier constraint is active and the second one is inactive. (c) Does this satisfy the first order necessary conditions? Explain.
Answers
The first-order necessary conditions for the given NLP problem involve the KKT conditions, and a specific solution satisfying these conditions needs further analysis.
(a) The first-order necessary conditions for constrained optimization problems are defined by the KKT conditions. These conditions require that the gradient of the objective function be orthogonal to the feasible region, the constraints be satisfied, and the Lagrange multipliers be non-negative.
(b) Assuming the first Lagrangian multiplier constraint is active means that it holds with equality, while the second one is inactive implies that it does not affect the solution. By incorporating these assumptions into the KKT conditions and solving the resulting equations along with the given constraints, a solution can be obtained.
(c) To determine if the solution satisfies the first-order necessary conditions, one needs to verify if the obtained values satisfy the KKT conditions. This involves checking if the gradient of the objective function is orthogonal to the feasible region, if the constraints are satisfied, and if the Lagrange multipliers are non-negative. Only by performing this analysis can it be determined if the solution satisfies the first-order necessary conditions.
Learn more about solution here:
https://brainly.com/question/28221626
#SPJ11
Differentiate implicitly to find the first partial derivatives of z. 11x2 + 2y^2 + 5z^2 = 4 ϑz/ϑx =
ϑz/ϑy =
Answers
The first partial derivatives of z are:
∂z/∂x = -22x / (10z)
∂z/∂y = -4y / (10z)
To find the first partial derivatives of z with respect to x and y in equation 11x^2 + 2y^2 + 5z^2 = 4, we will differentiate the equation implicitly with respect to x and y.
First, let's find ∂z/∂x:
Differentiate both sides of the equation with respect to x:
22x + 0 + 10z(∂z/∂x) = 0
Now, solve for ∂z/∂x:
10z(∂z/∂x) = -22x
∂z/∂x = -22x / (10z)
Next, let's find ∂z/∂y:
Differentiate both sides of the equation with respect to y:
0 + 4y + 10z(∂z/∂y) = 0
Now, solve for ∂z/∂y:
10z(∂z/∂y) = -4y
∂z/∂y = -4y / (10z)
So, the first partial derivatives of z are:
∂z/∂x = -22x / (10z)
∂z/∂y = -4y / (10z)
Learn more about the first partial derivatives: https://brainly.com/question/30217886
#SPJ11
During halloween, 8 out of 25 students in Mrs. Murphy's class wore a costume. What was the probability that an individual student wore a costume
Answers
Answer:
32%
Step-by-step explanation:
An art gallery displays a large painting in the center of a wall that is 242424 feet (\text{ft})(ft)left parenthesis, start text, f, t, end text, right parenthesis wide. The painting is 10\,\text{ft}10ft10, start text, f, t, end text wide. Which of the following equations can be used to find the distances, xxx, in feet, from the left end of the wall to the edges of the painting
Answers
The equation that can be used to find the distances from the left end of the wall to the edges of the painting is x = 12 - 5/2 × 10.
The painting is centered on the wall, so the distance from the left end of the wall to the center of the painting is 12 feet. The painting is 10 feet wide, so the distance from the center of the painting to each edge is 5 feet. Therefore, the distance from the left end of the wall to each edge of the painting is 12 feet - 5 feet = 7 feet.
The equation x = 12 - 5/2 × 10 can be used to calculate this distance. The variable x represents the distance from the left end of the wall to the edge of the painting, 12 represents the distance from the left end of the wall to the center of the painting, and 5/2 × 10 represents the distance from the center of the painting to the edge of the painting.
The other equations listed are not correct because they do not take into account the fact that the painting is centered on the wall. The equation x = 10 would be correct if the painting were placed flush against the left end of the wall. The equation x = 24 - 10 would be correct if the painting were placed flush against the right end of the wall.
Learn more about distances here:
brainly.com/question/15172156
#SPJ11
help pleasee! with Proof of work! :))

Answers
Answer:
w = 4
x = 3
y = -2
z = 5
Step-by-step explanation:
You can see how I got the answer on the pic that I gave

Find the exact length of the third side.
10
6
PLEASE HELP GUH

Answers
Answer:
8
Step-by-step explanation:
I'm using this equation: a^2+b^2=c^2
x^2+6^2=10^2
x^2+36+100
x^2= 64
x=sqrt64
x=8
I NEED HELP ASAP PLEASE

Answers
Answer:
<A= 92
<C=88
<H= 92
Step-by-step explanation:
Angle <E is equal to <H because they are vertical angles.
Angle <E is equal to <A because they are corresponding angles.
Angle <E and <C are supplementary because they are interior angles on the same side of a transversal, 180-92=88
PLEASE HELP MEEEEEEEEEEEEEEEEEEEEEEEEEEE!!!!!!!!!!!! WILL GIVE BRAINLIEST IF RIGHT! 2 PPPL HAVE TO ANSWER FIRST

Answers
Answer: J
Step-by-step explanation:
\(log_2 24 - log_2 3 = log_2 (24/3) = log_2 8 = 3\)
So \(log_5 x = 3 -> x=125\)
In the rainforest of Puerto Rico, I needed to measure the height of a really tall tree. I used a device to measure the angle of elevation from my line of sight to the top of a tree to be 31°. Find the height of the tree if my height is 6 feet and I was 275 feet from the tree
Answers
Answer:
Step-by-step explanation:
See image

What is the equation in point-slope form of the line that passes through the point (4,-5) and has a slope of 2/3?
Answers
Answer:
m = 8 / -2 = 4 / -1 = -4
Step-by-step explanation:
Which shows how to find the value of this expression when X=-2 and y = 5?
(3xy-22
32 (-2)
54
3(-2)6
54
32 (5)
(-2)*
3
(2) 654
Answers
Answer:
it's the first one
Step-by-step explanation:
I got it right on edge
The requried, expression to find the value of the given expression when x =-2 and y = 5 is 3²(-2)⁶/5⁴. Option A is correct.
What does simplification mean?In order to remove pointless terms, factors, or operations from an expression, arithmetic, and algebraic principles are applied. The objective is to get an expression that is simpler to use, manipulate, or solve. For instance, factoring, merging like terms, or applying the distributive property can all be used to simplify an algebraic statement.
Here,
Given expression,
= (3x³y⁻²)²
To find the solution of the above expression given value of x and y,
= (3(-2)³(3)⁻²)²
= (3²(-2)⁶/3⁴)
Thus, the required expression to find the value of the given expression when x =-2 and y = 5 is 3²(-2)⁶/5⁴. Option A is correct.
Find out more about simplification by visiting this link: brainly.com/question/12501526
#SPJ7
A work crew can
pave 3/4 of a mile
of the interstate
in 6 3/4 hours.
What is their unit
rate for paving
the interstate?
Answers
Answer: 1/9 of a mile per hour
=========================================================
Explanation:
6 & 3/4 = 6 + 3/4 = 24/4 + 3/4 = (24+3)/4 = 27/4
The work crew paves 3/4 of a mile in 27/4 hours. Divide those two fractions:
(3/4) divide (27/4)
(3/4) times (4/27)
(3*4)/(4*27)
3/27
1/9
The unit rate is 1/9 of a mile per hour. In other words, for each hour, they are able to pave 1/9 of a mile on average. So we should expect it takes about 9 hours to pave a full mile.
Your friend is celebrating her 25 th birthday today and wants to start saving for her anticipated retirement at age 65 . She wants to be able to withdraw $250,000 from her saving account on each birthday for 20 years following her retirement; the first withdrawal will be on her 66th birthday. Your friend intends to invest her money in a retirement account, which earns 8 percent return per year. She wants to make an equal annual deposit on each birthday into the account for her retirement fund. Assume that the annual return on the retirement account is 8 percent before retirement and 5 percent after retirement. If she starts making these deposits on her 26 th birthday and continue to make deposits until she is 65 (the last deposit will be on her 65 th birthday and the total number of annual deposits is 40), what amount must she deposit annually to be able to make the desired withdrawals at retirement? (Hint: One way to solve for this problem is to first find the value on your friend's 65 th birthday of the $250,000 withdrawal per year for 20 years after her retirement using the annual return after retirement and then find the equal annual deposit that she needs to make from her 26th birthday to 65 th birthday using the annual return before retirement.) Ignore taxes and transaction costs for the problem.
Answers
The correct answer is your friend needs to deposit approximately $13,334.45 annually from her 26th birthday to her 65th birthday to be able to make the desired withdrawals at retirement.
To determine the annual deposit your friend needs to make for her retirement fund, we'll calculate the present value of the desired withdrawals during retirement and then solve for the equal annual deposit.
Step 1: Calculate the present value of the withdrawals during retirement
Using the formula for the present value of an annuity, we'll calculate the present value of the $250,000 withdrawals per year for 20 years after retirement.
\(PV = CF * [1 - (1 + r)^(-n)] / r\)
Where:
PV = Present value
CF = Cash flow per period ($250,000)
r = Rate of return after retirement (5%)
n = Number of periods (20)
Plugging in the values, we get:
PV = $250,000 * \([1 - (1 + 0.05)^(-20)] / 0.05\)
PV ≈ $2,791,209.96
Step 2: Calculate the equal annual deposit before retirement
Using the formula for the future value of an ordinary annuity, we'll calculate the equal annual deposit your friend needs to make from her 26th birthday to her 65th birthday.
\(FV = P * [(1 + r)^n - 1] / r\)
Where:
FV = Future value (PV calculated in Step 1)
P = Payment (annual deposit)
r = Rate of return before retirement (8%)
n = Number of periods (40)
Plugging in the values, we get:
$2,791,209.96 = \(P * [(1 + 0.08)^40 - 1] / 0.08\)
Now, we solve for P:P ≈ $13,334.45
Therefore, your friend needs to deposit approximately $13,334.45 annually from her 26th birthday to her 65th birthday to be able to make the desired withdrawals at retirement.
Learn more about compound interest here:
https://brainly.com/question/24274034
#SPJ11
Write –3/8 as a decimal number.
Answers
Answer:
-0.375
Step-by-step explanation:
you just divide the numbers.
In a statistic class, 11 scores were randomly selected with the following results were obtained: 68,74,66,37,52.71,90,65.76,73,22. What are the inner fences?
15.0,130.0
220.1020
97.0,1070
19.0,1060
54.0.860
Answers
The inner fences for a set of 11 scores, as given in the question, are 15.0 and 130.0.
The lower inner fence is found by subtracting 1.5 times the interquartile range (IQR) from the lower quartile (Q1), and the upper inner fence is found by adding 1.5 times the IQR to the upper quartile (Q3). The IQR is the difference between Q3 and Q1.
In this case, the given scores are 68, 74, 66, 37, 52, 71, 90, 65, 76, 73, and 22. To find the inner fences, we first need to calculate Q1 and Q3. After sorting the scores in ascending order, we find that Q1 is 52 and Q3 is 74. The IQR is then calculated as Q3 - Q1, which gives us 22.
Finally, we can calculate the lower inner fence by subtracting 1.5 times the IQR from Q1: 52 - (1.5 * 22) = 15.0. Similarly, the upper inner fence is found by adding 1.5 times the IQR to Q3: 74 + (1.5 * 22) = 130.0.
Therefore, the inner fences for the given set of scores are 15.0 and 130.0. These values can be used to identify potential outliers in the data.
Learn more about Interquartile here
https://brainly.com/question/29173399
#SPJ11
Ao and bo are two equal roads meeting at an angle of 60. a and b are joined by a straight road ab and also by a radial road acb. find to the nearest metre by how much the radial road is longer than the straight line
Answers
The radial road is longer than the straight line by approximately 0.154 m. Therefore, the required answer is 0.154 m.
Given: AO = BO, ∠AOB = 60°, and AB is joined by straight road ACB and radial road AB.
To Find: By how much radial road AB is longer than the straight line?
Let's construct the diagram below, In triangle AOB, using the sine rule:
AB / sin ∠ABO = BO / sin ∠BAO, AB / sin 60° = BO / sin 60° => AB = BO ...(i)
Let AC = BC = x m ∴ AB = 2x m (Since ∠AOC = ∠BOC = 60°)
In triangle ABC, using the cosine rule:AB² = AC² + BC² - 2ACBC cos ∠CAB(2x)² = x² + x² - 2(x)(x)(cos 120°)4x² = 2x² + x² + 2(x² )∴ x² = 2x² / 3 => x = (2 / √3)x
Let AD be the perpendicular distance of C from AB.
Then, AD = (x)sin 60° = (x√3 / 2) m And BD = (x)sin 30° = (x / 2) m
Thus, AB = AD + BD = (x√3 / 2) + (x / 2) = (2x + x√3) / 2From eq. (i), we have BO = 2x m
Therefore, radial road ACB is longer than straight line AB by = ACB - AB= (2x + x√3) / 2 - 2x= x(√3 - 2) / 2= [2 / √3]× [√3 - 2]≈ 0.154 m
Learn more about sine:
https://brainly.com/question/30162646
#SPJ11