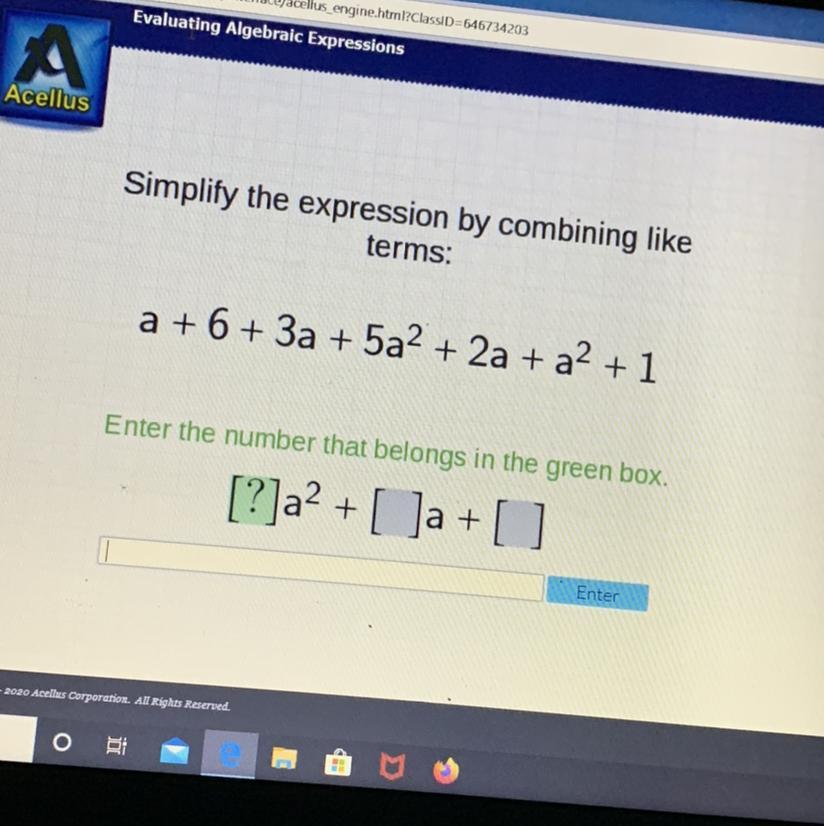
Answers
Answer:
6
Step-by-step explanation:
you combine the a2 with 5a2 as they are the only ones with a squared, combine and you get 6a2 + 6a + 7
Related Questions
I don’t know how to solve for x or y, I’m knew to this and CANT remember the formula

Answers
Answer:
\( \frac{6}{x} = \frac{8}{24} \)
\(8x = 144\)
\(x = 18\)
\( \frac{8}{24} = \frac{y}{12} \)
\(24y = 96\)
\(y = 4\)
So x = 18 and y = 4.
Evaluate the expression: 5 + 3 × (5 - 2)²
Answers
Answer: 32
Step-by-step explanation:
5+3*(5-2)^2
5+3*(3)^2
5+3*9
5+27
32
Answer:
32
Step-by-step explanation:
5 + 3 * (5 - 2)^2
5 + 3 * 3^2
5 + 3 * 9
5 + 2
= 32
Sorry if it's a bother, but what's the answer to these? I'm having a little bit of trouble.

Answers
~Let's change 9.9² to 10² since we have to estimate.~
We know that:
10² = 100Given expression: 9.9² × 1.79Solving the expression:
9.9² × 1.79=> 10² × 1.79=> 100 × 1.79=> 179The estimated value of 9.9² × 1.79 is 179.
Solution (b):~Let's change √97.5 to √100 and 1.96 to 2 since we have to estimate.~
We know that:
√100 = 10Given expression: √97.5 ÷ 1.96Solving the expression:
√97.5 ÷ 1.96=> √100 ÷ 2=> 10 ÷ 2=> 5The estimated value of √97.5 ÷ 1.96 is 5.
Can someone please help me I don’t know how to do this please
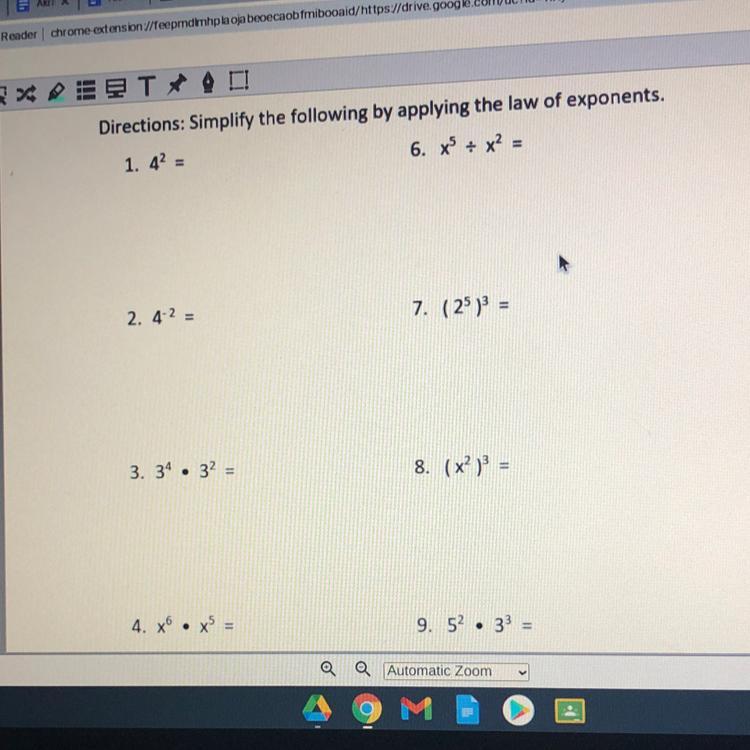
Answers
Answer:
2. 1/16
3. 729
4. x^11
6. x^3
7. 32768
8. x^6
9. 675
THIS IS THE QUESTION HELP ME FIND THE AREA PLS

Answers
The total area of the composite figure is; 94.485 sq.units
How to find the area of the composite shape?The given composite shape is made up of a rectangle and the quadrant of a circle.
Formula for area of rectangle is;
A_r = Length * Width
Thus;
A_r = 8 * 7
A_r = 56 sq.units
The formula for the area of the quadrant of a circle is;
A_quad = ¹/₄πr²
Thus;
A_quad = ¹/₄π * 7²
A_quad = 38.485 sq.units
Total area of composite figure = 56 sq.units + 38.485 sq.units
= 94.485 sq.units
Read more about Area of composite shape at; https://brainly.com/question/10254615
#SPJ1
Please help. click picture to get rest of question. zoom in if needed The linear function f(x) = 0.2x + 79 represents the average test score in your math class, where x is the number of the test taken. The linear function g(x) represents the average test score in your science class, where x is the number of the test taken.

Answers
Explanation:
Part A.
f(x) gives us the average test score, so to calculate the average test score n your math class after test 2, we need to replace x by 2 in f(x), then:
\(\begin{gathered} f(x)=0.2x+79 \\ f(2)=0.2\cdot2+79 \\ f(2)=79.4 \end{gathered}\)Therefore, the test average for your math class is 79.4
Part B.
To find the test average for your science class after test 2, we need to know what is the value of g(x) when x is equal to 2.
Since g(x) is 84 when x is 2, the test average for your science class is 84.
Part C.
After completing test 4, the average of the math class is:
\(\begin{gathered} f(4)=0.2\cdot4+79 \\ f(4)=79.8 \end{gathered}\)On the other hand, we can see that after a new test, the average of the science class g(x) decreases by 2. So, after completing test 4 g(x) will be
For the function F defined by F(x)=x^2-2x+4 find F(2b-1).
Answers
Answer:
F(2b-1) = 4b² - 6b + 4
Step-by-step explanation:
Replace all the x with 2b-1
F(x) = x² - 2x + 4
F(2b-1) = (2b-1)² - 2(b) + 4
= 4b² - 4b + 1 - 2b + 4
= 4b² - 6b + 4
In triangle QRS, Q = (8x), m/R = (14x+2)°, and m/S= (10x +50)°. What is the measu
A. 4°
B. 32°
C. 58°
D. 90°
Please select the best answer from the choices provided
OA
OB
D
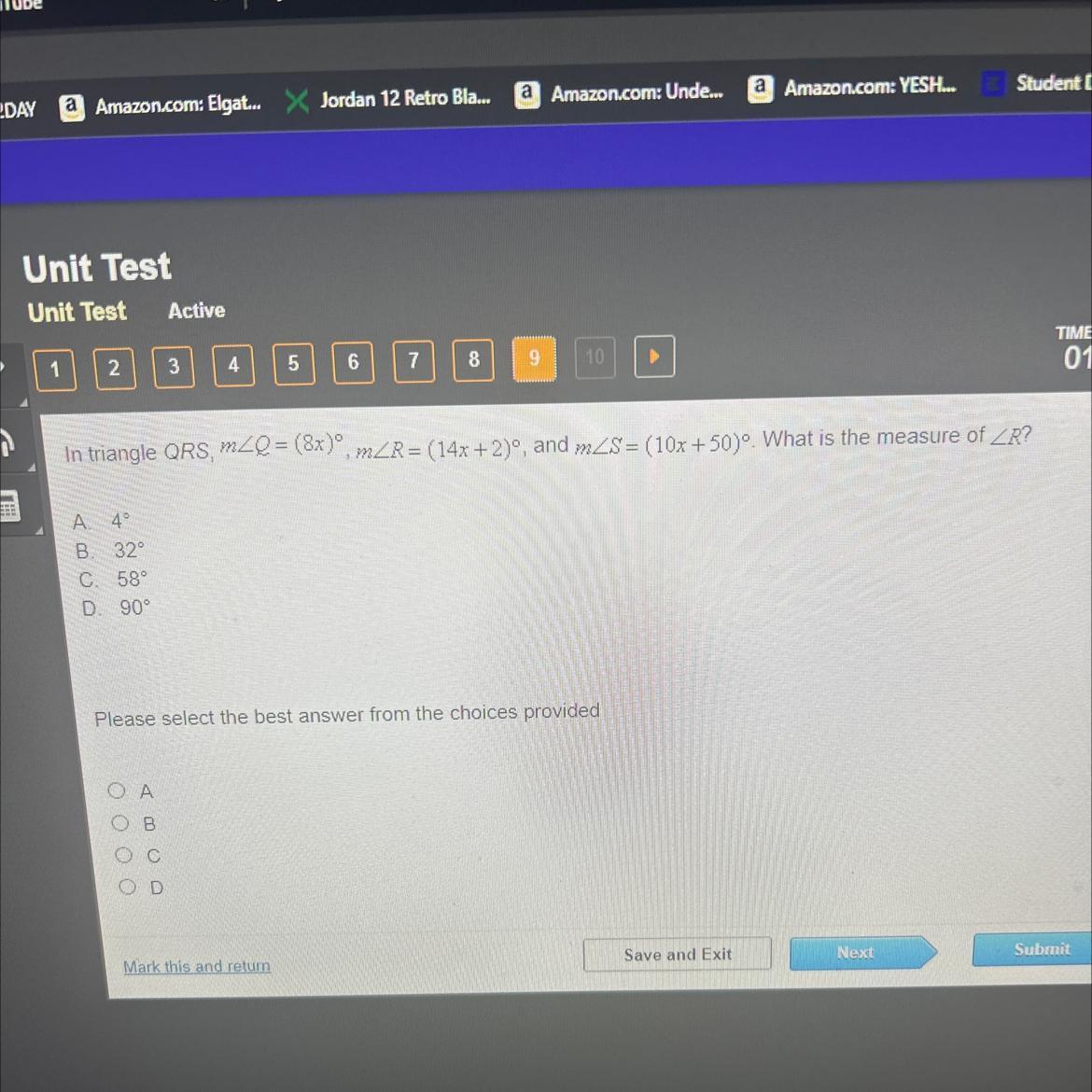
Answers
Answer:
C. 58 degrees
To find the measure of angle R in triangle QRS, we can use the fact that the sum of the angles in a triangle is 180 degrees.
Given:
Q = 8x
m/R = 14x + 2 degrees
m/S = 10x + 50 degrees
The sum of angles Q, R, and S is 180 degrees:
Q + R + S = 180
Substituting the given values:
8x + (14x + 2) + (10x + 50) = 180
Simplifying the equation:
8x + 14x + 2 + 10x + 50 = 180
32x + 52 = 180
32x = 180 - 52
32x = 128
x = 128/32
x = 4
Now that we have the value of x, we can substitute it back into the given expressions to find the measures of angles Q, R, and S.
Q = 8x = 8 * 4 = 32 degrees
m/R = 14x + 2 = 14 * 4 + 2 = 58 degrees
m/S = 10x + 50 = 10 * 4 + 50 = 90 degrees
Therefore, the measure of angle R is 58 degrees. So, the correct answer is C. 58°.
I hope you do great and pass this Unit test!!
Q1: Use the given information to answer the question regarding similiar triangles
Q2: Triangle SHE is similiar to Triangle RHY


Answers
1) The length of the side DE by similar triangle theorem is; Option C: 20
3) If RY = b + 4 and SE =20, then the value of b is; 6
How to find the lengths of similar triangles?Similar triangles are defined as triangles that have the same shape, but their sizes may vary. Thus, we can say that equilateral triangles, squares of any side lengths are as well examples of similar objects. This means that, if two triangles are similar, then their corresponding angles are congruent and corresponding sides are in equal proportion.
1) ΔABC ~ ΔDEF
We are given the similar triangles ABC and DEF.
We are also told that ΔABC ~ ΔDEF.
Now, If AB = 10, AC = 8 and DF = 16
Thus, by similar triangle theorem, we can apply it to the attached triangle to get;
AB/DE = AC/DF
DE = (AB * DF)/AC
DE = (10 * 16)/8
DE = 20
3) Now, by using the concept of similar triangles, since we are given that;
R is the midpoint of line SH.
Y is the midpoint of line EH
RY = b + 4
SE =20
(b + 4)/20 = 1/2
Cross multiply to get;
2(b + 4) = 20
2b + 8 = 20
2b = 20 - 8
b = 12/2
b = 6
Read more about similar triangles at; https://brainly.com/question/14285697
#SPJ1

Question 1
Identify the percent of change as an increase or a decrease.
50 pounds to 35 pounds
Answers
There is percent decrease of 30%
We have to find the percent of change :50 pounds to 35 pounds
Original amount = 50 pounds
New amount= 35 pounds
Since, New amount is less than the original amount, this is a percentage of decrease.
Change in amount = 35 -50
Change in amount = -15 pounds
Substitute the given values we have;
% change = (change/original value) x 100
% change = -(15/50) x 100
% change = - 30%
Therefore, there is percent of decrease which is 30%.
Learn more about percentages here : https://brainly.com/question/24304697
#SPJ1
The joint density function of X and Y is given by : f(x,y) ={xe^-(x+y) x>0, y>0
{0 otherwise
Are X and Y independent?
My question is how do you determine if X and Y are independentof each other with the given information? I am unsure of how toapproach this problem.
Answers
The value of X and Y are not independent of each other.
To determine if X and Y are independent or not from each other with the given information, we have to check if the given joint density function satisfies the following property:
f(x,y) = g(x) × h(y)
where g(x) and h(y) are the marginal density functions of X and Y respectively.
If the above equation holds, then X and Y are said to be independent of each other.If not, X and Y are dependent on each other.
Let's find the marginal density functions of X and Y.
The marginal density function of X:
fX(x) = ∫f(x,y)dy
∫0∞xe^-(x+y)dy = x
∫0∞e^-(x+y)dy∫0∞e^-(x+y)dy = x
The marginal density function of Y:fY(y) = ∫f(x,y)dx∫0∞xe^-(x+y)dx = e^-y
The joint density function doesn't satisfy the property:
f(x,y) ≠ g(x) × h(y)f(x,y) = x × e^-(x+y)
fX(x) = x
fY(y) = e^-y
Since the joint density function can not be expressed as the product of the marginal density functions of X and Y, X and Y are dependent on each other.
Learn more about function at
https://brainly.com/question/32583830
#SPJ11
Point K is on line segment JL. Given KL = 3 and JL = 13, determine the length
JK.
Answers
Answer: JK=10
Step-by-step explanation:
JL=JK+KL
13=JK+3
13-3=JK+3-3
JK=10
I NEED TO KNOW NOW IT'S DUE!!
Last summer, Fred earned 16 dollars per day, and Maria earned 18 dollars per day together, they earned 1780 dollars. If Fred worked 5 more days than Maria, how many days did Maria work?
Answers
x = # of days Maria worked
x + 5 = # of days Fred worded
$16(x + 5) + $18x = $1780
Let's distribute the $16
$16x + $80 + $18x = $1780
Combine like terms
$34x + $80 = $1780
Subtract $80 from both sides.
$34x = $1700
Divide both sides by $34
x = 50 days
Maria worked 50 days
What’s the algebraic expression of this expression? Only answer if you know

Answers
Answer:
a³ + 5c
Step-by-step explanation:
That would be, symbolically, a³ + 5c
Sarah works for the Urban Pollination Project. Five years ago, 25% of urban gardens were visited by native bees, and Sarah would like to know if this proportion is different now than it was five years ago. Sarah collects her data and analyzes the data She calculates a p-value of 0.178. Using a significance level of 0.05, what is the best conclusion? A. Fail to reject the null hypothesis. There is sufficient evidence to support the claim that the proportion of urban gardens visited by native bees is different than 25%
B. Reject the null hypothesis. There is enough evidence to support the null hypothesis C. The null hypothesis is true D. Fall to roject the null hypothesis. There is not sufficient evidence to support the claim that the proportion of urban gardens visited by native bees is different than 25%
Answers
Using a significance level of 0.05, we can conclude that fails to reject the null hypothesis. There is not sufficient evidence to support the claim that the proportion of urban gardens visited by native bees is different than 25%. The correct option is d).
Based on the given information, Sarah has calculated a p-value of 0.178 and is using a significance level of 0.05. The p-value is a measure of the strength of evidence against the null hypothesis. In hypothesis testing, if the p-value is less than the chosen significance level (0.05 in this case), it suggests that the observed data is statistically significant and provides evidence to reject the null hypothesis.
On the other hand, if the p-value is greater than the significance level, it indicates that the observed data is not statistically significant, and there is insufficient evidence to reject the null hypothesis.
In this scenario, since the p-value (0.178) is greater than the significance level (0.05), the best conclusion is to "Fail to reject the null hypothesis." This means that there is not sufficient evidence to support the claim that the proportion of urban gardens visited by native bees is different than 25%. The data collected does not provide strong enough evidence to conclude that there has been a significant change in the proportion over the five-year period.
Therefore, the correct answer is D. "Fail to reject the null hypothesis. There is not sufficient evidence to support the claim that the proportion of urban gardens visited by native bees is different than 25%."
Know more about significance level here:
https://brainly.com/question/31070116
#SPJ11
Use the appropriate compound-angle formula to express the following as a single trigonometric function, and then determine
the exact value of the expression.
sin π/2 cos π/4 - cos π/2 sin π/4
Answers
Answer:
\(\frac{1}{\sqrt{2}}\)
Step-by-step explanation:
Help plzz I think it is 1 or 2 ..... By The square root property, if k is a real number and x^2=k, then what is x equal to? 1. √k 2. =| √k 3. -√k 4. k^2
Answers
Answer:
\(\Large \boxed{2. \ x=\pm \sqrt{k}}\)
Step-by-step explanation:
\(x^2 =k\)
k is a real number.
We take the square root of both sides of the equation.
\(\sqrt{x^2 } =\pm \sqrt{k}\)
Simplifying the equation.
\(x=\pm \sqrt{k}\)
Answer:
x = ±√k
Step-by-step explanation:
If:
\(x^2 = k\)
We'll take square root on both sides
=> \(\sqrt{x^2} = +/- \sqrt{k}\)
=> x = ±√k
5/11x6/7 = 5/14.........................................
Answers
Because 5/11x6/7 =30/77
Answer:
\(5 \div 11 \times 6 \div 7 = \frac{30}{77} \)
(GIVING BRAINLIEST!!!)
What is the total length of all the ski trails that are 2 7/8 miles long?
Answers
Answer:
\(Total\ length = 8\frac{5}{8}\ miles\)
Step-by-step explanation:
Given
See attachment for ski trails
Required
Total length of \(2\frac{7}{8}\) ski trails
From the attached figure, there are 3 skis with length \(2\frac{7}{8}\ miles\)
So:
The total length is:
\(Total\ length = 3 * 2\frac{7}{8}\)
Express fraction as improper fraction
\(Total\ length = 3 * \frac{23}{8}\)
\(Total\ length = \frac{3 *23}{8}\)
\(Total\ length = \frac{69}{8}\)
\(Total\ length = 8\frac{5}{8}\ miles\)

1/a-1 -1/a+1 - 2/2a+1 - 2/2a-1
Answers
Answer:
-2-\(\frac{2}{a}\)
Step-by-step explanation:
I broke up the fractions so that it is easier.
\(\frac{1}{a-1}\) - \(\frac{1}{a+1}\) - \(\frac{2}{2a+1}\) - \(\frac{2}{2a-1}\) = (\(\frac{1}{a}\) - \(\frac{1}{1}\)) - (\(\frac{1}{a}\) + \(\frac{1}{1}\)) - (\(\frac{2}{2a}\) + \(\frac{2}{1}\)) - (\(\frac{2}{2a}\) - \(\frac{2}{1}\))
Now I remove the brackets. One plus and one minus make one minus and two minus makes one plus.
(\(\frac{1}{a}\) - \(\frac{1}{1}\)) - (\(\frac{1}{a}\) + \(\frac{1}{1}\)) - (\(\frac{2}{2a}\) + \(\frac{2}{1}\)) - (\(\frac{2}{2a}\) - \(\frac{2}{1}\)) =\(\frac{1}{a}\) - \(\frac{1}{1}\) - \(\frac{1}{a}\) - \(\frac{1}{1}\) - \(\frac{2}{2a}\) - \(\frac{2}{1}\) - \(\frac{2}{2a}\) + \(\frac{2}{1}\)
Remove redundancies. (\(\frac{1}{a}\) - \(\frac{1}{a}\) = 0)
\(\frac{1}{a}\) - \(\frac{1}{1}\) - \(\frac{1}{a}\) - \(\frac{1}{1}\) - \(\frac{2}{2a}\) - \(\frac{2}{1}\) - \(\frac{2}{2a}\) + \(\frac{2}{1}\) = -\(\frac{2}{1}\) -\(\frac{4}{2a}\)
Simplify the fractions.
-\(\frac{2}{1}\) -\(\frac{4}{2a}\) = -2-\(\frac{2}{a}\)
A number y, when rounded to 2 decimal places, is equal to 9.68.
Find the upper and lower bound of y.
Answers
When rounding a number to 2 decimal places, we are essentially keeping only the first two digits after the decimal point and discarding the rest. The third digit after the decimal point is the one that affects the rounding decision.
In this case, the number y is rounded to 9.68, which means that the third digit after the decimal point is either 5 or greater than 5. If it is 5 or greater, we round up the second digit after the decimal point. If it is less than 5, we simply truncate the decimal part.
To find the upper bound of y, we need to add 0.005 to 9.68, which is the smallest possible value for the third digit that would cause rounding up:
9.68 + 0.005 = 9.685
Therefore, the upper bound of y is 9.685.
To find the lower bound of y, we need to subtract 0.005 from 9.68, which is the largest possible value for the third digit that would not cause rounding up:
9.68 - 0.005 = 9.675
Therefore, the lower bound of y is 9.675.
Hence, the upper and lower bounds of y are 9.685 and 9.675, respectively.
In a fraction with a denominator of 15, which value could the numerator be to produce a repeating decimal?
A. 15
B. 9
C. 11
D. 12
Answers
Answer:
11
Step-by-step explanation:
Step 1:
\(\frac{11}{15}\) = 0.7333333333333
Miguel has triple David's money, while Lisbeth has ten dollars less than David. The sum of their money totals $95. How much money does David have?
Answers
Answer:
Miguel has $63
Lisbeth has $11
David has $21
Step-by-step explanation:
let Miguel share be M
let Lisbeth share be L
let David share be D
from the question, we know that
M=3D
L=D-10.
M+L+D=95
thus,
3D+(D-10)+D= 95
3D+D-10+D= 95
5D-10 = 95
5D= 95+10
5D= 105
D= 105/5
D= 21.
thus,
M = 3D = 3×21
= $63
L = D-10 = 21-10
= $11
(63+21+11)$ = $95
A chemical company makes up batches of copper sulfate solution by adding 250 kg of copper sulfate powder to 1000 liters of water. A laboratory chemist wants to make a solution of identical concentration, but only needs 350 mL (0.35 liters) of solution.
How much copper sulfate powder should the chemist add to the water? Enter your answer in the box below in decimal format.
The mass of copper sulfate that the chemist should add is ___
kg.
I will give brainylest if correct
Answers
Answer:
mass is 58kg
Step-by-step explanation:
PLSSS HELPPP
give me the answers and explain

Answers

The side lengths of triangle ABC are 22, 2X and 55 The side lengths of triangle DEF are 11, 5, 5.5x is it possible that the triangles are similar?

Answers
Answer:
Yes, it is possible that the triangles ABC and DEF are similar. To check if two triangles are similar, one must check if all the corresponding angles are equal. To do this, we need to find the measure of triangle ABC's interior angles. We can use the Triangle Sum Theorem, which states that the sum of any triangle's three interior angles is equal to 180 degrees. So, if we subtract 22 + (2X) + 55 from 180, we get 180 - 77 = 103. Therefore, triangle ABC's interior angle measures are 22, (2X), and 103.
To determine if the two triangles are similar, we must also find the interior angle measures of triangle DEF. We can do this by subtracting 11 + 5 + (5.5X) from 180, which gives us 180 - 16.5 = 163.5. Therefore, triangle DEF's interior angle measures are 11, 5, and 163.5.
Now, since all the pairs of corresponding angles are equal (22 and 11; 2X and 5; and 103 and 163.5), the triangles ABC and DEF do have the possibility of being similar.
you take a random of twenty ksu students and find that 16 of them have jobs. what is the probability that you would find exactly 16 out of twenty have jobs if the .50 conjectured by the professor was correct? what is the probability that you would find 16 or more have jobs? what will you say to the professor?
Answers
The probability of exactly 16 students having jobs in the sample is 0.204 and the probability of 16 or more students having jobs in the sample is 0.334.
Let X be the number of KSU students with jobs in a random sample of 20 students. Since each student in the sample can be either employed or not employed, X follows a binomial distribution with parameters n = 20 (the sample size) and p = 0.50 (the probability of a student having a job).
To find the probability of exactly 16 students having jobs in the sample, we can use the binomial probability mass function
P(X = 16) = (20 choose 16) * 0.5^16 * 0.5^(20-16) = 0.204
To find the probability of 16 or more students having jobs in the sample, we can use the cumulative distribution function
P(X ≥ 16) = 1 - P(X < 16) = 1 - ∑(i=0 to 15) (20 choose i) * 0.5^i * 0.5^(20-i) = 0.334
Based on the sample data, it appears that the proportion of KSU students with jobs is higher than the professor's conjectured value of 0.50. However, we cannot conclusively reject the professor's conjecture based on a single sample of 20 students.
We would need to conduct a hypothesis test with appropriate statistical significance level to determine if the difference between the sample proportion and the conjectured value is statistically significant or not.
To know more about probability here
https://brainly.com/question/28813679
#SPJ4
Ray BD bisects 2ABC. Use the diagram and the given angle measure to
find m2ABC. (Keyword = BISECTS)

Answers
Since ray BD bisects angle ABC we can set the two angle measures given equal to each other.
2x+7=4x-41
Solve for x=24
Plug in the x to find angle ABD 2(24)+7=55
therefore angle ABD is 55 and angle DBC is 55 so angle ABC is 110
Use the Laplace transform to solve the given initial-value problem.
y'' ? 7y' + 12y = ??(t ? 1), y(0) = 0, y'(0) = 1
y(t) =??
Answers
Taking the inverse Laplace transform of Y(s), we get: y(t) = (f(t) + 3e²3t - 4e²4t) u(t - 1) where u(t - 1) is the unit step function (equal to 0 for t < 1 and equal to 1 for t >= 1).
To solve the differential equation y'' - 7y' + 12y = f(t), we first take the Laplace transform of both sides:
L[y''] - 7L[y'] + 12L[y] = L[f(t)]
Using the properties of the Laplace transform and the initial conditions, we can simplify the left-hand side as follows:
s²2 Y(s) - s y(0) - y'(0) - 7 (s Y(s) - y(0)) + 12 Y(s) = L[f(t)]
s²2 Y(s) - s - 7s Y(s) + 12 Y(s) = L[f(t)]
Y(s) (s²2 - 7s + 12) = L[f(t)] + s
Solving for Y(s), we get:
Y(s) = (L[f(t)] + s) / (s²2 - 7s + 12)
To find the inverse Laplace transform of Y(s), we factor the denominator:
s²2 - 7s + 12 = (s - 3)(s - 4)
Using partial fractions, we can write Y(s) as:
Y(s) = A/(s - 3) + B/(s - 4)
where A and B are constants. Multiplying both sides by the denominator (s - 3)(s - 4) and setting s = 3 and s = 4, we can solve for A and B:
A = (L[f(t)] + 3) / (4 - 3) = L[f(t)] + 3
B = (L[f(t)] + 4) / (3 - 4) = -L[f(t)] - 4
Therefore, Y(s) can be written as:
Y(s) = (L[f(t)] + 3)/(s - 3) - (L[f(t)] + 4)/(s - 4)
Taking the inverse Laplace transform of Y(s), we get:
y(t) = (f(t) + 3e²3t - 4e²4t) u(t - 1)
where u(t - 1) is the unit step function (equal to 0 for t < 1 and equal to 1 for t >= 1).
learn more about equation here:
brainly.com/question/29538993
#SPJ11
How do you find the gradient of a line?
Answers
Answer:
To calculate the gradient of a straight line you choose two points on the line itself.
From the two points we calculate:
The difference in height (y co-ordinates) ÷ The difference in width (x co-ordinates).
If the answer is a positive value then the line is uphill in direction.
If the answer is a negative value then the line is downhill in direction.
Step-by-step explanation: