The owner of a small deli is trying to decide whether to discontinue selling magazines. He suspects that only 10% of his customers buy a magazine and he thinks that he might be able to use the display space to sell something more profitable. Before making a final decision, he decides that for one day he will keep track of the number of customers that buy a magazine. Assuming his suspicion that 10% of his customers buy a magazine is correct, what is the probability that exactly 5 out of the first 13 customers buy a magazine?
Answers
Answer:
0.55% probability that exactly 5 out of the first 13 customers buy a magazine
Step-by-step explanation:
For each customer, there are only two possible outcomes. Either they buy a magazine, or they do not. The probability of a customer buying a magazine is independent of other customers. So we use the binomial probability distribution to solve this question.
Binomial probability distribution
The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.
\(P(X = x) = C_{n,x}.p^{x}.(1-p)^{n-x}\)
In which \(C_{n,x}\) is the number of different combinations of x objects from a set of n elements, given by the following formula.
\(C_{n,x} = \frac{n!}{x!(n-x)!}\)
And p is the probability of X happening.
10% of his customers buy a magazine
This means that \(P = 0.1\)
What is the probability that exactly 5 out of the first 13 customers buy a magazine?
This is P(X = 5) when n = 13. So
\(P(X = x) = C_{n,x}.p^{x}.(1-p)^{n-x}\)
\(P(X = 5) = C_{13,5}.(0.1)^{5}.(0.9)^{8} = 0.0055\)
0.55% probability that exactly 5 out of the first 13 customers buy a magazine
Answer:
\( P(X=5) = (13C5) (0.1)^5 (1-0.1)^{13-5}= 0.00554\)
So then he probability that exactly 5 out of the first 13 customers buy a magazine is 0.0554
Step-by-step explanation:
Let X the random variable of interest "number of customers that buy a magazine", on this case we can model the variable of interest with this distribution:
\(X \sim Binom(n=13, p=0.1)\)
The probability mass function for the Binomial distribution is given as:
\(P(X)=(nCx)(p)^x (1-p)^{n-x}\)
Where (nCx) means combinatory and it's given by this formula:
\(nCx=\frac{n!}{(n-x)! x!}\)
We want to find this probability:
\( P(X=5)\)
And using the probability mass function we got:
\( P(X=5) = (13C5) (0.1)^5 (1-0.1)^{13-5}= 0.00554\)
So then he probability that exactly 5 out of the first 13 customers buy a magazine is 0.0554
Related Questions
Find the 75th term of the following arithmetic sequence 16,25,34,43
Answers
Answer:
\(\boxed {\boxed {\sf 682}}\)
Step-by-step explanation:
The nth term of an arithmetic sequence can be found using the following formula.
\(a_n=a+d(n-1)\)
where a is the first term, d is the common difference, and n is the term.
First, we should find the common difference.
We can do this by subtracting each term from the term following it. Basically, subtract the first term from the second term, the second from the third, and so on.
\(d= a_2-a_1\)
The second term is 25 and the first is 16.
\(d= 25-16\)
\(d=9\)
Now we know the common difference is 9. We also know the first term is 16 and we are looking for the 75th term.
\(d=9 \\a=16 \\n= 75\)
Substitute the values into the formula.
\(a_{75}=16+9(75-1)\)
Solve according the PEMDAS (Parentheses, Exponents, Multiplication, Division, Addition, Subtraction).
Solve the parentheses first.
\(a_{75}=16+9(74)\)
Multiply next.
\(a_{75}=16+666\)
Finally, add.
\(a_{75}=682\)
The 75th term in the sequence is 682.
Put the answer please!

Answers
The inequality that represents the interval shown on the number line is:
5 ≤ x ≤ 9
How to express the interval shown?We want to use inequality notation to define the interval shown on the number line.
We can see that the first point is marked with a closed circle, at x = 5.
And then we have another closed circle at x = 9
The closed circles means that these points are solutions to the inequality, so we need to use the symbols:
≤ and ≥
Then we can write the inequality:
5 ≤ x ≤ 9
Learn more about inequalities:
https://brainly.com/question/24372553
#SPJ1
Here's the work I've done. Is it right?
V=πr^2h
π(0.375)^2(0.80)
=0.4m^3 (smallest cylinder)
π(0.625)^2(0.80)
=1.0m^3 (middle cylinder)
0.70+0.80
=1.5m (height for big cylinder)
π(1.5)^2(1.5)
=10.6m^3
10.6m^3+0.4m^3+1.0m^3
=12.0m^3
The spa will fit 12.0m^3 of water

Answers
Answer: \(6.67m^3\)
Step-by-step explanation:
For hemisphere...
diameter (d1) = 3m
radius (r1) = (3/2)m
The total volume of the hemisphere
\(v1=\frac{2}{3} \pi (r1)^3\)
\(=\frac{2}{3} \pi (\frac{3}{2} )^3\)
\(=\frac{9}{4} \pi\)
-----------------------------------------------------------------------
For smaller cylinder
diameter (d2) = 0.75
radius (r2) = 0.75/2m
height (h2) = 0.80m
Volume of smaller cylinder
(V2) = \(\frac{1}{3} \pi (r2)^2h2\)
\(=\frac{1}{3} \pi (\frac{0.75}{2} )^2*0.80\)
\(=\frac{3}{80} \pi\)
------------------------------------------------------------------------
For bigger cylinder
Volume of bigger cylinder =
\(V3=\frac{1}{3} \pi (\frac{1.25}{2} )^2*0.70\)
\(=\frac{35}{384} \pi\)
-----------------------------------------------------------------------
Volume of water = \((v1 - v2 - v3) =\frac{9}{4} \pi -\frac{3}{80} \pi -\frac{35}{384} \pi = 6.67 m^3\)
A lot of points. PLEASE HELP! I will mark brainliest. Whoever gets it right first.

Answers
- the last one is your answer, you can use the small lines on the side of triangle to help you know which ones match with each other
Prove that the only automorphism of a well-ordered set is the identity?
Answers
The only automorphism of a well-ordered set is the identity.
To prove this statement, we need to show that any automorphism of a well-ordered set must be the identity function. An automorphism is a bijective function that preserves the order structure of the set.
Assume we have a well-ordered set (W, ≤), where W is the set and ≤ is the order relation.
Let f: W → W be an automorphism of the set.
We aim to prove that f is the identity function, i.e., f(x) = x for all x ∈ W.
Suppose, for contradiction, that there exists an element a ∈ W such that f(a) ≠ a.
Since f is a bijective function, there must exist some b ∈ W such that f(b) = a.
Since (W, ≤) is well-ordered, there is a least element c in the set {x ∈ W : f(x) ≠ x}.
Let d = f(c). Since f is an automorphism, f(c) ≠ c, and thus d ≠ c.
Since (W, ≤) is well-ordered, there is a least element e in the set {x ∈ W : f(x) = d}.
Consider the element f(e). Since f is a bijective function, there must exist some f^{-1}(f(e)) = e' ∈ W such that f(e') = f(e) = d.
By the definition of automorphism, f(f^{-1}(y)) = y for all y ∈ W. Applying this property to e', we have f(f^{-1}(f(e'))) = f(e') = d.
However, f^{-1}(f(e')) = e' ≠ c, and thus f(e') ≠ d. This contradicts the fact that e is the least element in the set {x ∈ W : f(x) = d}.
Therefore, our assumption that there exists an element a such that f(a) ≠ a is false.
Since we assumed f(a) ≠ a for arbitrary a ∈ W, it follows that f(x) = x for all x ∈ W.
Hence, the only automorphism of a well-ordered set is the identity function.
Therefore, we have proven that the only automorphism of a well-ordered set is the identity function.
For more such questions on automorphism, click on:
https://brainly.com/question/30894112
#SPJ8
What is the distance between the points (-2,1) and (5,-4)
Answers
Considering the definition of distance between two points, the distance between the points (-2,1) and (5,-4) is √74= 8.6023.
Distance between two pointsThe distance between two points is equal to the length of the segment that joins them. Therefore, to determine the distance between two different points, you must calculate the squares of the differences between their coordinates and then find the root of the sum of said squares.
In other words, the distance between two points in space is the magnitude of the vector formed by said points.
So, given the coordinates of two distinct points (x1, y1) and (x2, y2), the distance between two points is the square root of the sum of the squares of the difference of the coordinates of the points:
distance= \(\sqrt{(x2-x1)^{2} +(y2-y1)^{2} }\)
Distance between the points (-2,1) and (5,-4)In this case, you know:
(x1, y1): (-2,1)(x2, y2): (5,-4)Replacing in the definition of distance:
distance= \(\sqrt{(5-(-2))^{2} +(-4-1)^{2} }\)
distance= \(\sqrt{(5+2)^{2} +(-5)^{2} }\)
distance= \(\sqrt{7^{2} +(-5)^{2} }\)
distance= \(\sqrt{49+25 }\)
distance= √74= 8.6023
Finally, the distance between the points (-2,1) and (5,-4) is √74= 8.6023.
Learn more about distance between two points:
https://brainly.com/question/23848540
https://brainly.com/question/7243416
https://brainly.com/question/15973889
#SPJ1
The interest earned on rs15000 in 3 years at simple interest is rs5400 find the rate of interest per anunm
Answers
Answer:
12%
Step-by-step explanation:
Let the rate of interest be R%
r = R% as decimal =R/100
Simple interest earned for 3 years at rate r on ₹15,000 = ₹5,400
The formula for interest earned is given by
I = Prt
where P is the principal amount (15,000)
r = annual interest rate as a decimal (to be determined)
t = number of years
Plugging in known values we get
5400 = 15000 x r x 3
= 45000 x r
r = 5400/45000
r = 0.12
Rate of interest as a percentage = r x 100 = 0.12 x 100 = 12%
Pankaj is a Biomedical Engineering student. He plans to deposit $600 that he earned as stipend, in
a bank account at 3% rate of interest compounded weekly for no more than 2 years. The total
amount of the money, A, that Pankaj will get back, is a function of time, t. Which is a reasonable
domain of the money that he may accumulate?

Answers
The correct answer is A: 600 <= money <= 2822.4.
This represents the range of possible values that Pankaj's accumulated money could fall into, given the specified conditions of the 3% interest rate compounded weekly for a maximum of 2 years. The lower bound, 600, represents the initial deposit amount, while the upper bound, 2822.4, represents the maximum amount of money Pankaj could earn after 2 years, assuming that interest is compounded every week.
Find the surface area of the cone in terms of π.
180π cm2
108π cm2
144π cm2
90π cm2

Answers
Answer:
\(54\pi \: {cm}^{2} \)
Step-by-step explanation:
Given:
A cone
l = 15 cm
r (radius) = 3 cm
Find: A (surface area) - ?
\(a(surface) = \pi {r}^{2} + \pi \times r \times l\)
\(a(surface) = \pi \times {3}^{2} + \pi \times 3 \times 15 = 9\pi + 45\pi = 54\pi \: {cm}^{2} \)
PLEASE HELP ME
The following data set shows the pulse rate of some goats at a farm:
75, 76, 77, 76, 77, 76, 78, 75, 78, 76, 79, 76, 78, 76, 77, 76
Which dot plot best represents the data?
dot plot with 2 dots over 75, 8 dots over 76, 3 dots over 77, 3 dots over 78, no dot over 79
dot plot with 2 dots over 75, 7 dots over 76, 3 dots over 77, 3 dots over 78, 1 dot over 79
dot plot with 1 dot over 75, 8 dots over 76, 3 dots over 77, 3 dots over 78, 1 dot over 79
dot plot with 2 dots over 75, 6 dots over 76, 3 dots over 77, 3 dots over 78, 1 dot over 79
Answers
Answer: B) dot plot with 2 dots over 75, 7 dots over 76, 3 dots over 77, 3 dots over 78, 1 dot over 79
Step-by-step explanation: took the test, hope this helps c:
Evaluate f(x) = 3x + 8 for x = 1.
-11
5
11
3

Answers
Answer:
11
Step-by-step explanation:
f(x)=3x+8
f(1)=3(1)+8
f(1)=3+8
f(1)=11
Answer:
The anwser is 11
Step-by-step explanation:
You just replace x with 1, and solve, so it would be 3(1) + 8, which is 11.
What is the slope of the graph y=-3×
I need help
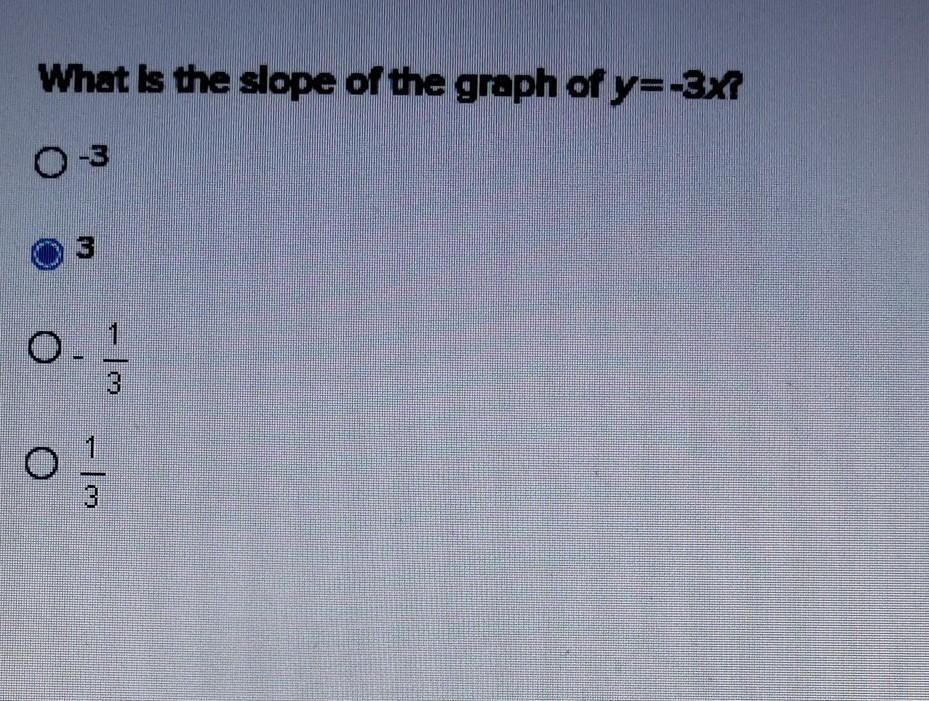
Answers
Answer:
-3
Step-by-step explanation:
the graph is the coefficient so it is the number before x
Answer:
-3
Step-by-step explanation:
Slope describes the rate of change between the change in y and the change in x. What the equation tells us is that y decreases by 3 each time (aka. increasing by -3) when x increases by 1. This gives us a slope of -3.
please help me i really need help

Answers
Answer:
68
Step-by-step explanation:
15% of 80 is 12 so you subtract 12 from 80 and thats 68.
A spinner is divided into five colored sections that are not of equal size: red, blue, green, yellow, and purple. The spinner is spun several times, and the results are recorded below:
Spinner Results
Color Frequency
Red 4
Blue 4
Green 15
Yellow 9
Purple 3
Based on these results, express the probability that the next spin will land on blue or green or purple as a percent to the nearest whole number.
Answers
Step-by-step explanation:
OUT of 35 spins 4 + 15 + 3 = 22 were blue or green or purple
22/35 probability = 63%
what is (y-4)= -5/7 (x+28) in slope intercept form
Answers
Answer:
y = (-5/7)x - 16
Step-by-step explanation:
(y - 4)= -5/7(x + 28)
y - 4= -5/7x - 20
+4 +4
------------------------
y = (-5/7)x - 16
I hope this helps!
Answer: \(y =-\frac{5}{7}x -16\)
Step-by-step explanation:
The slope-intercept form is y = mx + b, where m is the slope, and b is the y-intercept.
\((y-4)= -\frac{5}{7} (x+28)\)
\(y -4=(-\frac{5}{7})(x) + (-\frac{5}{7})(28)\)
\(y -4=-\frac{5}{7}x + (-20)\)
\(y -4=-\frac{5}{7}x -20\) Add 4 on both sides.
\(y =-\frac{5}{7}x -16\)
Which mathematical equation correctly represents the statement, 6 less than twice the difference of a number and 8 is equal to 14?© 2(n - 8) - 6 = 14(n-8) - 6 = 146 -2(n - 8) = 146- (n - 8) = 14

Answers
You have the following statement:
- 6 less than twice the difference of a number and 8 is equal to 14.
To determine the algebraic expression of the previous situation, you analize by parts the previous sentence.
- The difference of a number and 8: it can be taken as n - 8
- Twice the difference of a number and 8: 2(n - 8)
- 6 less than twice the difference of a number and height: 6 - 2(n - 8)
Thus, the algebraic equation is:
6 - 2(n - 8) = 14
my friend needs help with this can someone help

Answers
Answer:Sorry
Step-by-step explanation:
Hi would help but i dont know and im not in collage sorry.
CAN SOMEONE HELP ME WITH THIS PLS I'LL MARK AS BRAINLIEST,, SHOW COMPLETE SOLUTION PLS:D

Answers
Step-by-step explanation:
The side lengths of the kite are marked
TOTAL perimeter will be 25 + 25 + 35 + 35 = 120 cm
10 Per Question :), Algebra 2





Answers
The value of the expression is 16x(x+1) / 10x² -14x -12
What is algebraic expression?In mathematics, an algebraic expression is an expression built up from constant algebraic numbers, variables, and the algebraic operations (addition, subtraction, multiplication, division and exponentiation by an exponent that is a rational number)
The given expression is
16/(x-2) ÷ 4/(x+1) + 6/x
Simplify this to have
16 / (x-2) ÷ (10x + 6) / (x+1)(x)
this implies that 16/(x-2) * (x+1)(x)/(10x +6)
16(x² + x)/(x-2)(10x+6)
Therefore the value of the expression is
16x(x+1) / 10x² -14x -12
learn more about simplification of algebraic expressions on https://brainly.com/question/11894863
#SPJ1
Simplify and express in exponential form: 8^-1 * 3^3/ 2^-4 * 9^-2
Answers
Answer:
2^1* 3^7
Step-by-step explanation:
8^-1 * 3^3/ 2^-4 * 9^-2
Negative exponents move from the numerator to the denominator or from the denominator to the numerator
2^4*9^2* 3^3 /8^1
Rewriting 9^2 as 3^2^2 = 3^4 and 8 = 2^3
2^4 * 3^3 * 3^4 / 2^3
2^4/ 2^3 = 2 and 3^3 * 3^4 = 3^(3+4) = 3^7
2* 3^7
Answer:
Step-by-step explanation:
\(\frac{8^{-1}*3^{3}}{2^{-4}*9^{-2}}=\frac{(2^{3})^{-1} * 3^{3}}{2^{-4}*(3^{2})^{-2}}\\\\=\frac{2^{3*-1}*3^{3}}{2^{-4}*3^{2*-2}}\\\\=\frac{2^{-3}*3^{3}}{2^{-4}*3^{-4}}\\\\=2^{-3+4}*3^{3+4}\\\\=2^{1}*3^{7}\\\\=2*3^{7}\)
For a project in his Geometry class, Elijah uses a mirror on the ground to measure the height of his school building. He walks a distance of 8.25 meters from the school, then places a mirror on flat on the ground, marked with an X at the center. He then steps 0.8 meters to the other side of the mirror, until he can see the top of the school clearly marked in the X. His partner measures the distance from his eyes to the ground to be 1.45 meters. How tall is the school? Round your answer to the nearest hundredth of a meter.
Answers
The school is about 14.95 meters tall, and the mirror is 8.25 meters from the school.
What is trigonometric ratio?Trigonometric ratio is used to show the relationship between the sides and angles of a right angled triangle.
Let Ф represent the angle Elijah makes with the ground, hence:
tanФ = 1.45/0.8
Ф = 61.11°
The angle of elevation to the building is 61.11°. Let h represent the height of the building.
tan(61.11°) = h/8.25
h = 14.95
The school is about 14.95 meters tall, and the mirror is 8.25 meters from the school.
Find out more on trigonometric ratio at: https://brainly.com/question/24349828
Pls help me I will make brainlyest

Answers
Answer:
1/12, 30/360 and 30°
Explanation:
the fraction turns through 1/12 of the circle, as shown in the diagram.
1/12 = 30/360, because 360 ÷ 12 × 1 = 30.
thus, the measure of the angle is 30°.
i hope this helps! :D do comment if you have any questions.
A LOT OF POINTS!!!! PLZ ANSWER

Answers
Answer:
f(3x)= 3x+5/6x+2
substitute the value of X in the given question.
if u want simplified form then u can try rationalising.
f(3x)= 3x+5/6x+2 hope helped thanks for points
Homework part2 need help asap

Answers
The key features of the given quadratic functions are listed below.
What is the graph of a quadratic function?In Mathematics and Geometry, the graph of any quadratic function would always form a parabolic curve because it is a u-shaped. Based on the first quadratic function, we can logically deduce that the graph is an upward parabola because the coefficient of x² is positive and the value of "a" is greater than zero (0) i.e 3 > 0.
For the quadratic function y = 3x² - 5, the key features are as follows;
Axis of symmetry: x = 0.
Vertex: (0, -5).
Domain: [-∞, ∞]
Range: [-5, ∞]
For the quadratic function y = -2x² + 12x - 15, the key features are as follows;
Axis of symmetry: x = 3.
Vertex: (3, 3).
Domain: [-∞, ∞]
Range: [-∞, 3]
For the quadratic function y = -x² + 1, the key features are as follows;
Axis of symmetry: x = 0.
Vertex: (0, 1).
Domain: [-∞, ∞]
Range: [-∞, 1]
For the quadratic function y = 2x² - 16x + 30, the key features are as follows;
Axis of symmetry: x = 4.
Vertex: (4, -2).
Domain: [-∞, ∞]
Range: [-2, ∞]
Read more on quadratic functions here: brainly.com/question/24020644
#SPJ1

X (-9, 2) and Y(5, -4)
Given the points, find XY. Round to the nearest tenth.
Answers
Answer:
XY: 15.23
Step-by-step explanation:
Smartness
The distance between the endpoints of line segment XY will be 15.2 units.
What is the distance between two points?It is the measure of distance between the two points and is known as length. The length is measured in meters generally.
Let one point be (x, y) and another point be (h, k).
Then the distance between the points will be
D² = (x - h)² + (y - k)²
The endpoints of line segment XY are given below.
X(-9, 2) and Y(5, -4)
The distance between the endpoints of line segment XY will be given as,
D² = (x - h)² + (y - k)²
D² = (5 + 9)² + (-4 - 2)²
D² = (14)² + (-6)²
D² = 196 + 36
D² = 232
D = √232
D = 15.2 units
The distance between the endpoints of line section XY will be 15.2 units.
Learn more about the distance between two points here:
https://brainly.com/question/18296211
#SPJ2
Ron is planning for the back-to-school rush at his store. Last year he estimated that he would need 168 notebooks, but he sold 200 notebooks. Explain how Ron can find the percent error of his estimate.
Answers
Answer:
ਮੁਆਫ ਕਰਨਾ ਮੈਨੂੰ ਬਿੰਦੂ ਚਾਹੀਦੇ ਹਨ
Step-by-step explanation:
Answer:
9807654e6785e46754
Step-by-step explanation:
It's in the picture !

Answers
The position of √17 between 4 and 5, which is nearer 5, and the location of 6, which is between 2 and 3, which is nearer 2.
What is Number line?A visual representation of real numbers in a linear manner is a number line. It is a straight line that is divided into intervals or segments, each of which stands for a distinct real number value.
Number lines can be vertical or horizontally oriented, and they can also have a positive or negative orientation. Positive numbers often extend to the right or up, whereas negative numbers typically extend to the left or down. The origin of the number line, or zero, is typically situated in the middle of the line.
The number line is a crucial tool in mathematics since it offers a means of representing numerical relationships visually and carrying out fundamental arithmetic operations. For instance, positive and negative motions along a number line can be used to depict addition and subtraction, respectively, with positive movements denoting addition and negative movements denoting subtraction. On a number line, multiplication and division can alternatively be shown as repeated addition or subtraction.
If we have a number line with the proper markings, we may indicate where the square roots of 17 and 6 are located as follows:
To begin, determine the approximate square root values:
√17 is between 4 and 5, since 4² = 16 and 5² = 25.
√6 is between 2 and 3, since 2² = 4 and 3² = 9.
Place the number √17 closer to 5, between 4 and 5.
Place the number √6 between the numbers 2 and 3, closer to 2.
Since 6 and 17 are not integers and their values are not evenly spaced, it should be noted that their markings will not be evenly spaced on the number line.
To know more about Number Line, visit:
https://brainly.com/question/24644930
#SPJ1
Number line attached below,

Select all the correct answers. If the measure of angle is is , which statements are true? The measure of the reference angle is . The measure of the reference angle is . The measure of the reference angle is . cos(0)=-3/10
Answers
The measure of angle is θ cannot determine the statements that are true about its reference angle.
There are two issues with the given statement.
First, it does not specify the measure of angle θ.
Second, the statement cos(0)=-3/10 is not related to the reference angle of θ.
The reference angle of θ is the acute angle between the terminal side of θ and the x-axis.
It is always positive and its measure is between 0 and 90 degrees or between 0 and π/2 radians.
The measure of the reference angle of θ is denoted by θ'.
To determine the reference angle of θ, we need to know the quadrant in which θ lies.
The reference angle of θ in standard position is the acute angle between the terminal side of θ and the x-axis.
If θ is in the first quadrant, then θ' = θ.
If θ is in the second quadrant, then θ' = π - θ.
If θ is in the third quadrant, then θ' = θ - π.
If θ is in the fourth quadrant, then θ' = 2π - θ.
The measure of angle θ, we can determine its reference angle using the above rules.
The statement cos(0)=-3/10 is not related to the reference angle of θ.
It is the value of the cosine function at 0 radians or 0 degrees.
This value does not correspond to any angle that has a reference angle.
The measure of angle θ cannot determine the statements that are true about its reference angle.
For similar questions on measure of the angle
https://brainly.com/question/30741629
#SPJ11
HELP FAST PLSSSS IM DESPERATE RLLY

Answers
Which of the following is the correct interpretation of 2?
In a statistics class, a teacher had the students
complete an activity in which they grabbed as many
bite-sized pretzels as they could with their dominant
hand, without crushing them. The teacher then
measured their handspan in centimeters. A regression
analysis was completed and the value for was
52.1%
* About 52.1 percent of the variation in handspan is
accounted for by the linear relationship formed with
the number of bite-sized pretzels grabbed with the
dominant hand.
About 52.1 percent of the variation in number of
bite-sized pretzels grabbed with the dominant hand
is accounted for by the linear relationship formed
with handspan
About 47.9 percent of the variation in handspan is
accounted for by the linear relationship formed with
the number of bite-sized pretzels grabbed with the
dominant hand
About 72.1 percent of the variation in number of
bite-sized pretzels grabbed with the dominant hand
is accounted for by the linear relationship formed
with handspan
Answers
Answer:
B
Step-by-step explanation:
EDGEN
Answer:
B. About 52.1 percent of the variation in number of bite-sized pretzels grabbed with the dominant hand is accounted for by the linear relationship formed with handspan.
Step-by-step explanation:
