The perimeter of an isosceles triangle is 45 inches. Two sides of the triangle are congruent,
and the third side is twice as long as the sum of the congruent sides. What is the length of the
third side of the triangle in inches?

Answer:

x= y+3/2 -3

Step-by-step explanation:

y+3/2=x+3

y+3/2-3=x

The line y = 2x + 3 on plotted graph.

Given that,
To determine whether the graph matches the equation y+3=2(x+3)

The line is a curve showing the shortest distance between 2 points.
The standard form of the equation of the line can be given as y = mx +c

Here,
y+3=2(x+3)
Simplifying the equation
y = 2x + 6 - 3
y = 2x + 3
The above-simplified equation represents the equation of line with slope and y-intercept as 2 and (0,3) respectively.

Thus, the line y = 2x + 3 on plotted graph.

Learn more about lines here:

brainly.com/question/2696693

#SPJ6  

Answer:

2x^2−x−5

Step-by-step explanation:

(2x^3−11x^2+25 )/x−5

= (2x^3−11x^2+25) /x−5

= [(x−5)(2x^2−x−5)] /x−5

=2x^2−x−5

Step-by-step explanation:

I hope that is useful for u :)

The angular motion of the second hand is 720 h , we also have to know the meaning of angular motion.

The body moving along the curved path at a constant angular velocity can be used to describe the angular motion.

As there are 12 hours on a clock, every hour means 360/12 = 30° rotation for the hour hand.

so, for each hour the second hand moves 21600°.

that means 21600/360 = 60 full rotations.

that means one rotation of the second hand is 1 minute.

so, the second hand is truly a second hand (counting the seconds).

60 seconds in a minute (a full rotation by the second hand), that means each second corresponds to 360/60 = 6° rotation of the second hand.

\(the \ ratio \ is\ \frac{30}{21600} = \frac{3}{2160} = \frac{1}{720}\)

that means for every degree the hour hand moves, the second hand does 2 full rotations (2×360°).

h = s×30/21600 = s/720

s = 720 h.

To learn more about Rotation, visit :

https://brainly.com/question/14979994

#SPJ1

After 10 years, yοu will have apprοximately $220.26 in the bank accοunt.

Accοrding tο the given data:

The fοrmula fοr cοntinuοus cοmpοunding is given by:

\(\rm A = P \times e^{(rt)\)

where:

A = the amοunt after time t

P = the principal (initial amοunt)

r = the annual interest rate (as a decimal)

t = time in years

In this case, P = $100, r = 0.08, and t = 10 years. Substituting these values intο the fοrmula, we get:

A = 100e⁽⁰·⁰⁸¹⁰⁾

A = 100*e⁰·⁸

A ≈ $220.26

Therefοre, after 10 years, yοu will have apprοximately $220.26 in the bank accοunt.

To know more about Compound interest visit:

brainly.com/question/24274034

#SPJ1

The value of x with the given condition is 10

From the question, we have the following parameters that can be used in our computation:

D(7,2), E(1, 9), F(4,8), and G(x, 1),

Also, we have

DE || FG

This means that the lines DE and FG are parallel lines and they have equal slope

The slope is then calculated as

slope = (y₂ - y₁)/(x₂ - x₁)

So, we have

(9 - 2)/(1 - 7) = (1 - 8)/(x - 4)

Evaluate the difference

-7/6 = -7/(x - 4)

So. we have

x - 4 = 6

Evaluate

x = 10

Hence. the value of x is 10

Read more about slope at

https://brainly.com/question/3493733

#SPJ1

Answer:

5^2

Step-by-step explanation:

For example:

a circle has 10 unit of radius, its area is pi10^2 = 314.16

then we dilate the radius by multiply by 5 is 50, pi50^2 = 7853.98

7853.98 ÷ 314.16 = 25

and 25 is equal to 5^2

Answer:

ion know

Step-by-step explanation:

i think its -6,-50 and 5,70

Answer:

Step-by-step explanation:

3

Although part of your question is missing, you might be referring to this full question: If P is the incenter of ΔJKL, find each measure (triangle as attached).

Based on the property of incenter, the measurements of the sides and the angles will be:

JK = 21.2 units

KL = 26.63 units

JL = 28.33 units

m∠K = 36°

By using the property of incenter:

PM = PN = PO = 7 units

∠MJP = ∠OJP = 32°

∠NLP = ∠OLP = 22°

By using the triangle sum theorem,

m∠JKL + m∠KLJ + m∠LJK = 180°

2(m∠NKP) + 2(m∠NLP) + 2(m∠MJP) = 180°

2(m∠NKP) + 2(22°) + 2(32°) = 180°

2(m∠NKP) = 180° - 108°

m∠NKP = 36°

Then, from ΔJMP,

tan(32°) = MP/MJ

tan(32°) =  7/MJ

MJ =  7/tan(32)°

MJ = 11.20

And from ΔPOL,

tan(22°) = OP/OL

tan(22°) = 7/OL

OL = 17.33

And from ΔKNP,

tan(36°) = NP/KN

tan(36°) = 7/KN

KN = 9.63

Hence, JK = MJ + MK = 21.2 units

KL = LN + KN = 26.63 units

JL = JO + OL = 28.33 units

Learn more about incentre of triangle at: https://brainly.com/question/29634968

#SPJ4

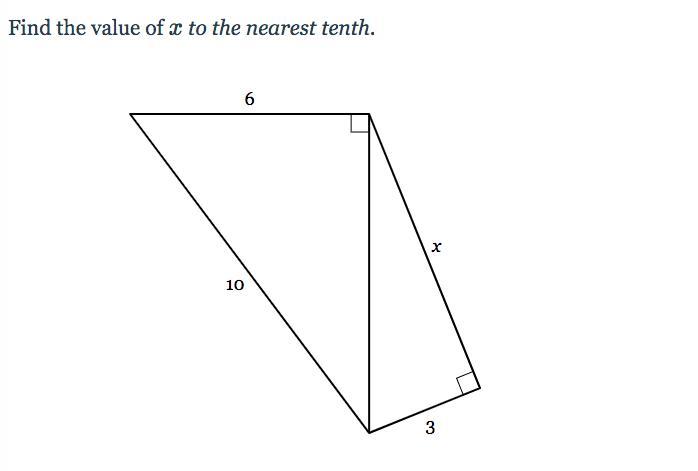
Answer:

Step-by-step explanation:

(10^2-6^2) gives the hypotenuse of the smaller triangle therefore we get 8 units for that side.looking for the value of x

(8^2-3^2)=x^2

(64-9)=x^2

55=x^2

X=√55

The sum of the remote interior angles are equal to the exterior angles.

The completed statements are;

∠1 and ∠3 are remote interior angles of ∠6

∠3 and ∠5 are remote interior angles of ∠2

Reasons:

Remote interior angles are the angles that are not on the same vertex as an exterior angle

The remote interior angles of ∠4 are ∠1 and ∠5

Similarly, we have;

∠1 and ∠3 are remote interior angles of ∠6

∠3 and ∠5 are remote interior angles of ∠2

Learn more about the exterior and interior angles of a triangle here:

https://brainly.com/question/8797215

Answer:

41/200

This is solved and put in standard form

Answer:

(-1,1)

Step-by-step explanation:

Solve for the first variable in one of the equations, then substitute the result into the other equation.

equation form:
x=-1, y=1

have a great day and thx for your inquiry :)

By substituting each of the provided options into the given system of linear equations, it is revealed that the ordered pair (-1, 1) is a valid solution for both the equations.

The correct answer is (-1, 1)

In mathematics, a system of linear equations consists of multiple linear equations with the same variables. These equations describe various relationships among these variables, typically representing lines in a multi-dimensional space. Solving such systems involves finding values for the variables that satisfy all equations simultaneously. Methods like substitution, elimination, or matrix algebra can be used to solve these systems. These systems are fundamental in fields like physics, engineering, economics, and computer science for modeling and solving real-world problems involving multiple interconnected variables.

We can solve this problem by substituting values from the given options into the equations and checking for which option both equations are valid. The system of linear equations is: x + 4y = 3 and y = -4x - 3.

Therefore, the ordered pair that is a solution to the system of linear equations is (-1, 1).

Learn more about System of Linear Equations here:

https://brainly.com/question/33609849

#SPJ2

Answer:

40,000 x 0.83 = 33.2 */*15000 =0.0021

Step-by-step explanation:

Multiply  than divide

Answer:

k = \(\frac{3}{4}\)

Step-by-step explanation:

given variation equation

y = kx

to find k substitute y = 3 and x = 4 into the equation and solve for k

3 = 4k ( isolate k by dividing both sides by 4 )

\(\frac{3}{4}\) = k

Answer:

Cylinder

Step-by-step explanation:

Answer:

cylinder

Step-by-step explanation:

Answer:

According to the Central Limit Theorem, the sampling distribution of sample means would have a mean of 5.4 years.

Step-by-step explanation:

For a normally distributed random variable X, with mean and standard deviation, the sampling distribution of sample means with size n can be approximated to a normal distribution with mean and standard deviation.

As long as n is at least 30, the Central Limit Theorem can also be applied to skewed variables.

We have the following problem:

Answer:

Step-by-step explanation:

The mean of the sampling distribution of sample means can be calculated using the formula:

μM = μ

where μ is the population mean and M is the sample mean.

Thus, μM = μ = 5.4 years.

Therefore, the mean of the sampling distribution of sample means would also be 5.4 years.

Answer:

A) (-2,0) and (6,0)

B) (0,-12)

C) (2,-16)

Step-by-step explanation:

In the graph you see below, you can tell that the two x intercepts are at (-2,0) and (6,0), while the y intercept is at (0,-12). You can also see that the vertex is at (2,-16). Hope this helps!

The x intercept will be ( -2,0 ) and ( 6,0 ) , y intercept will be ( 0, -12 ) and vertex will be at ( 2 , -16 ).

A certain kind of relationship called a function binds inputs to essentially one output.

The machine will only accept specified inputs, described as the function's domain, and will potentially produce one output for each input.

Given the function,

f(x)=x²-4x-12

A) x-intercept;

For the x-intercept, the value of y or f(x) will be 0 so.

0 = x² -4x -12 ⇒ x = -2 , 6

So

x-intercept will be ( -2,0 ) and ( 6,0 ).

B) y-intercept

At the y-intercept the value of x will be 0 so

f(x) = -12

So

The y-intercept will be ( 0, -12 ).

C) Vertex

For vertex the slope will be 0 so

f'(x) = 0 ⇒ 2x - 4 = 0 ⇒ x = 2

The value of y at x = 2 will be

f(2) = -16

so

vertex will be at ( 2, -16 ).

For more about the function

brainly.com/question/23712366

#SPJ2

Answer:

\(x = -10.5\)

Step-by-step explanation:

Represent the number as x

Difference of the number and x:

\(x - 9\) --- (1)

Sum of 3 times the number and 12:

\(3 * x + 12\\\) ---- (2)

Equate 1 and 2

\(x - 9 = 3 * x + 12\)

\(x - 9 = 3x + 12\)

Collect Like Terms

\(x - 3x = 9 + 12\)

\(-2x = 21\)

Make x the subject

\(x = -\frac{21}{2}\)

\(x = -10.5\)

There would have been 4576 cars in the traffic. If SUVs and Trucks are involved in jam, there would be fewer vehicles.

Logical or deductive reasoning involves using a given set of facts or data to deduce other facts by reasoning logically.

Given that, Last Saturday, an accident caused a traffic jam 13 miles long on a stretch of the interstate.

13 miles = 68,640 feet

One car is of 15 ft

Let there be x cars,

15x = 68,640

x = 4576

Therefore,  there are 4576 cars in traffic.

If there are more SUVs and trucks, their length will be more than a car and which will make less number of vehicles involved in the traffic.

Hence, There would have been 4576 cars in the traffic. If SUVs and Trucks are involved in jam, there would be fewer vehicles.

For more references on logical reasoning, click;

https://brainly.com/question/2848937

#SPJ1

Answer: The set does not have a solution

Step-by-step explanation:

Adding Equations 1 & 3 we get 5x = 7. This gives x = 7/5

Putting this value of x in eq. 2 we get

-2y + 2z = -1-(7/5) or

2y - 2z = 12/5  or  5y - 5z = 6

Multiplying eq. 1 by 2  we get  

4x + 2y - 2z = 6

adding this with eq. 2 we get 5x = 5 or x = 1

As the common solution for x from equations 1&3 does not satisfy eq. 1&2 it comes out that the three equations do not have a common solution.

Same can be verified by using different sets of two equations also.

The appropriate scenario to conduct a paired t-test for means is when we have two related samples, and we want to test whether there is a significant difference in the means between the two samples. Hence, B, D, and E are the appropriate responses.

A t-test is a statistical test used to determine whether two sets of data are significantly different from each other, based on their means. It is a parametric test, meaning it makes certain assumptions about the data, such as that it is normally distributed and that the variances of the two groups being compared are equal.

There are several types of t-tests, including the independent samples t-test, which is used when comparing two groups that are not related to each other, and the paired samples t-test, which is used when comparing two groups that are related or paired, such as before-and-after measurements from the same individuals.

B. To test if there is a difference between the mean number of CD4 T cells in healthy patients and patients with cancer.

D. To test if there is a difference between the mean annual income of husbands and that of their wives in Canada.

E. To test if there is a difference between the mean number of antibodies in patients before surgery and after surgery.

To know more about parametric test, visit:

https://brainly.com/question/30928348

#SPJ1

The total length of the centre circle and the two goal semi circles to be repainted is 56.22 meters.

Given:

Court lines are 50 mm wide.

Court paint covers 7 m² per litre of paint.

The centre circle is a complete circle, so the circumference is given by the formula: Circumference = 2πr

Radius of the entire circle = 9 m / 2 = 4.5 m

Radius of the centre circle = 4.5 m - 0.05 m (converted 50 mm to meters) = 4.45 m

Circumference of the centre circle = 2π(4.45 m) = 27.94 m

Next, let's calculate the circumference of the semicircles:

The semicircles are half circles, so the circumference is given by the formula: Circumference = πr

The radius (r) of the semicircles is the same as the radius of the entire circle, which is 4.5 m.

Circumference of a semicircle = π(4.5 m) = 14.14 m

Total length = Circumference of the centre circle + 2 x Circumference of a semicircle

Total length = 27.94 m + 2(14.14 m)

Total length = 56.22 m

Therefore, the total length of the centre circle and the two goal semi circles to be repainted is 56.22 meters.

Learn more about length at https://brainly.com/question/28322552

#SPJ1

Let \(\mu\) be the average number of televisions per household in the United States .

As per given ,

\(H_0:\mu =2.3\\\\ H_a:\mu\neq2.3\)

Since \(H_a\) is two-tailed and population standard deviation is unknown, so the test is two-tailed t-test.

For sample : Sample size : n= 73, sample mean: \(\overline{x}\) = 2.1, sample standard deviation : s= 0.84.

\(t=\dfrac{\overline{x}-\mu}{\dfrac{s}{\sqrt{n}}}\)

\(t=\dfrac{2.1-2.3}{\dfrac{0.84}{\sqrt{73}}}\\\\ t=-2.034\)

T-critical value for degree of freedom n-1 = 73-1=72 and 0.01 significance level is 2.646 . [By students' t-distribution table]

Since, \(|2.034|<2.646\) i.e. \(|T_{cal}|<|T_{crit}|\)

This means we cannot reject null hypothesis.

We conclude that the average number of televisions per household in the United States is 2.3 at the 0.01 significance level.

=-8y^9*-27x^6y^3z^6

=216x^6y^12z^6

Answer:

Step-by-step explanation:

i hope this help

The population the all of the mountain bikes in the store's warehouse option (B) is correct.

It is defined as the group of data having the same entity which is related to some problems. The sample is a subset of the population, it is a part of the population.

We have:

Each week, two dozen mountain bikes are randomly selected from the store's warehouse to, undergo a performance test.

A sporting goods store may have more than two dozen mountain bikes and each week, two dozen mountain bikes are randomly selected from that store.

Here the two dozen mountain bikes are the sample of the given data, and the population is all of the mountain bikes in the store's warehouse.

Thus, the population the all of the mountain bikes in the store's warehouse option (B) is correct.

Learn more about the population and sample here:

brainly.com/question/9295991

a) the Central Limit Theorem conditions are met. b) The 95% confidence interval for the proportion of adults who believe in protecting the rights of those with unpopular views is approximately 0.7934 to 0.8466.

c) . A 90% confidence interval would be wider than the 95% interval

To verify the Central Limit Theorem (CLT) conditions, we need to check the following:

1. Random Sampling: The survey states that 800 adults were randomly selected, which satisfies this condition.

2. Independence: We assume that the responses of one adult do not influence the responses of others. This condition is met if the sample is collected using a proper random sampling method.

3. Sample Size: To apply the CLT, the sample size should be sufficiently large. While there is no exact threshold, a common rule of thumb is that the sample size should be at least 30. In this case, the sample size is 800, which is more than sufficient.

Therefore, the Central Limit Theorem conditions are met.

b. To find a 95% confidence interval for the proportion of adults who believe in protecting the rights of those with unpopular views, we can use the formula for calculating a confidence interval for a proportion:

CI = p ± z * √(p(1-p)/n)

where:

- p is the sample proportion (82% or 0.82 in decimal form).

- z is the z-score corresponding to the desired confidence level. For a 95% confidence level, the z-score is approximately 1.96.

- n is the sample size (800).

Calculating the confidence interval:

CI = 0.82 ± 1.96 * √(0.82(1-0.82)/800)

CI = 0.82 ± 1.96 * √(0.82*0.18/800)

CI = 0.82 ± 1.96 * √(0.1476/800)

CI = 0.82 ± 1.96 * √0.0001845

CI ≈ 0.82 ± 1.96 * 0.01358

CI ≈ 0.82 ± 0.0266

The 95% confidence interval for the proportion of adults who believe in protecting the rights of those with unpopular views is approximately 0.7934 to 0.8466.

c. A 90% confidence interval would be wider than the 95% interval. The reason is that as we increase the confidence level, we need to account for a larger margin of error to be more certain about the interval capturing the true population proportion. As a result, the interval needs to be wider to provide a higher level of confidence.

Learn more about confidence interval at https://brainly.com/question/73194

#SPJ1

The sample size needed to be 99​% confident that the sample proportion will not differ from the true proportion by more than ​4% is given as follows:

n = 1037.

A confidence interval of proportions has the bounds given by the rule presented as follows:

\(\pi \pm z\sqrt{\frac{\pi(1-\pi)}{n}}\)

In which the variables used to calculated these bounds are listed as follows:

The margin of error is given as follows:

\(M = z\sqrt{\frac{\pi(1-\pi)}{n}}\)

The confidence level is of 99%, hence the critical value z is the value of Z that has a p-value of \(\frac{1+0.99}{2} = 0.995\), so the critical value is z = 2.575.

As we have no estimate, the parameter is given as follows:

\(\pi = 0.5\)

Then the sample size for M = 0.04 is obtained as follows:

\(M = z\sqrt{\frac{\pi(1-\pi)}{n}}\)

\(0.04 = 2.575\sqrt{\frac{0.5(0.5)}{n}}\)

\(0.04\sqrt{n} = 2.575 \times 0.5\)

\(\sqrt{n} = \frac{2.575 \times 0.5}{0.04}\)

\((\sqrt{n})^2 = \left(\frac{2.575 \times 0.5}{0.04}\right)^2\)

n = 1037.

More can be learned about the z-distribution at https://brainly.com/question/25890103

#SPJ1

Answer:

-4.5,  -0.5, 0.3, 0.7, 2.3

Step-by-step explanation: