the square root of the sum of twice a number and 3 is 6. find the number
Answers
Answer in fraction form = 33/2
Answer in decimal form = 16.5
===========================================================
Work Shown:
n = some number
2n = twice that number
2n+3 = "sum of twice a number and 3"
\(\sqrt{2n+3}\) = square root of the previous expression
The equation we need to solve is \(\sqrt{2n+3} = 6\)
We'll follow PEMDAS in reverse, undoing each operation, to isolate n
\(\sqrt{2n+3} = 6\\\\\left(\sqrt{2n+3}\right)^2 = 6^2 \ \ \text{ ... square both sides}\\\\2n+3 = 36\\\\2n+3-3 = 36-3 \ \ \text{ ... subtract 3 from both sides}\\\\2n = 33\\\\\frac{2n}{2}=\frac{33}{2} \ \ \text{ ... divide both sides by 2}\\\\n = \frac{33}{2}\\\\n = 16.5\)
Answer:
\(\frac{33}{2}\)
Step-by-step explanation:
In the problem, "The square root of the sum of twice a number and 3 is 6" can be converted to an equation that looks like this:
Let x be the number:
\(\sqrt{2x+3 = 6 }\)
In order to solve the problem:
\(\sqrt{2x+3}^2=6^2\)
By squaring both sides to remove the exponent:
\({2x + 3 = 36}\)
Simplify:
\({2x+3-3=36-3}\)
Subtract 3 from both sides:
\({2x = 33 }\)
Then Simplifying further:
\(\frac{2x}{2} = \frac{33}{2}\)
Divide both sides by 2 to remove 2 from the x.
\({x = \frac{33}{2} }\)
Thus, meaning the answer is \(\frac{33}{2}\)
Hope this helps you.
Related Questions
15)
136⁰
2
S
?
R
Find the measure of the arc or angle indicated
Answers
Answer:
224
Step-by-step explanation:
360.-136.
A bag contains 10 green,8 blue, and 2 white balls. Naomi seclets 2 balls from the bag at random, one at a time, without replacing them. What is the probability that she selects all two white balls?
E.) 2/95
F.) 1/95
G.) 1/190
H.) 1/380
Answers
To find the probability that Naomi selects both white balls, we need to consider the total number of possible outcomes and the number of favorable outcomes.
Total number of outcomes:
Naomi selects 2 balls without replacement, so the total number of outcomes is the number of ways she can choose 2 balls out of the total number of balls in the bag. This can be calculated using combinations:
Total outcomes = C(20, 2) = (20!)/(2!(20-2)!) = (20 * 19)/(2 * 1) = 190
Number of favorable outcomes:
Naomi needs to select 2 white balls. There are 2 white balls in the bag, so the number of favorable outcomes is the number of ways she can choose 2 white balls out of the 2 white balls in the bag:
Favorable outcomes = C(2, 2) = 1
Probability = Favorable outcomes / Total outcomes = 1/190
Therefore, the correct answer is (G) 1/190.
he button provides an automatic means of checking for mathematical errors within formulas of a worksheet.
Answers
The Error checking button provides an automatic means of checking for mathematical errors within formulas of a worksheet.
The modeling process begins with the framing of a conceptual model that shows the relationships between the various parts of the problem being modeled.
Arrows pointing from the selected cell to cells that depend on the selected cell are generated by using the Trace dependents button of the Formula Auditing group.
nodes in an influence diagram represent part of the model
The Trace Precedents button, located in the Formula Auditing group, creates arrows pointing to the selected cell from cells that are part of the formula in that cell
The Error checking button provides an automatic means of checking for mathematical errors within formulas of a worksheet.
To know more about error checking button brainly.com/question/1278871
#SPJ4
The circle graph represents the different kinds of plants the Martin family planted in their garden. Use the graph for Parts A-C.
Part A
If there are 200 plants in the garden, how many of them are green beans?
Part B
If there are 200 plants in the garden, which of the following represents the number of plants that are either pumpkin or tomato?
Part C
If there are 200 plants in the garden, which of the following represents how many more corn plants than cucumber plants there are?

Answers
Part A: There are 28 green beans in the garden. Part B: There are 80 plants that are either pumpkin or tomato. Part C: There are 52 more corn plants than cucumber plants.
What is a circle graph?A circle graph, often called a pie chart, is a circular graph with sectors on it, each representing a particular category or set of data. Each sector's area or angle is proportionate to the amount it stands for. In data visualisation, circle graphs are frequently used to show the relative sizes or proportions of several categories or groups within a dataset. They can instantly convey the distribution of data without the need for laborious numerical calculations, which makes them effective for presenting data that is divided into discrete groups. However, if the data is not presented in a clear and simple manner or if the sectors are not precisely drawn to scale, circle graphs may be deceiving.
Part A: The percentage of green beans in the circle graph is 14%.
14% of 200 = 0.14 x 200 = 28
Part B: The circle graph shows:
pumpkin plants and tomato plants is 20% + 20% = 40%.
40% of 200 = 0.40 x 200 = 80
Part C: The corn plants is 36% and the percentage of cucumber plants is 10%.
36% of 200 - 10% of 200 = (0.36 x 200) - (0.10 x 200) = 72 - 20 = 52
Learn more about circle graph here:
https://brainly.com/question/13298277
#SPJ1
Help me learn how to solve this please

Answers
The percentage that can be filled with $3 in 1990 is: 29.41%
How to solve percentage increase problems?To calculate percentage growth rate:
Beginning:
Calculate the difference (increase) between the two numbers you are comparing. after that:
Divide the increment by the original number and multiply the result by 100. Growth rate = increment / original number * 100.
We are told that it cost $3 to fill a gas tank as at 1970.
Now, there was a percentage price increase of (78.8 - 23.1)% = 55.2% from 1970 to 1990. Thus:
Cost of a gallon in 1970 = $0.36
Thus, number of gallons bought with $3 = 3/0.36 = 8.33 gallons at full tank
Now, in 1990, the cost is $1.23 and as such:
Quantity that can be bought = 3/1.23 = 2.45 gallons
Percentage of tank filled = 2.45/8.33 * 100% = 29.41%
Read more about Percentage increase at: https://brainly.com/question/11360390
#SPJ1
H
6:00 PM
What is a frostbite?
Answers
What single decimal multiplier would you use to decrease by 3% followed by a 4% increase?
Answers
Answer:
The single decimal multiplier is 26%.
Step-by-step explanation:
Since we have given that
You use to increase by 5% followed by 20% increase.
So, the single decimal multiplier would be
Hence, the single decimal multiplier is 26%.
After working for 24h Zoe made 234$ after working 40h zoe made 390$ predict how much she will make after 10h of work
Answers
Answer:
She will make $97.5 after 10 hours of work
Step-by-step explanation:
27.5% of US adults are college graduates.
A) Use StatKey or other technology to generate a sampling distribution for the sample proportion of college graduates using a sample size of n = 5. Generate at least 1000 sample proportions. Give the center of the sampling distribution and give the standard error.
B) Repeat part (a) using a sample size of n = 500.
C) If we took many samples of size 50 from the population of all inductees and recorded the proportion who were performers for each sample, what shape do we expect the distribution of sample proportions to have where do we expect it to be centered?
Answers
Complete Question
The complete question is shown on the first uploaded image
Answer:
a
center is 0.275
\(SE = 0.063\)
b
center is 0.275
\(SE = 0.020\)
Step-by-step explanation:
considering question a
From the question we are told that
The sample size is n = 50
The proportion of US adults are college graduates is p = 0.275
Generally the center is equivalent to the proportion so the center is 0.275
Generally the standard error is
\(SE = \sqrt{\frac{p * (1- p)}{ n} }\)
=> \(SE = \sqrt{\frac{0.275 * (1- 0.275)}{ 50} }\)
=> \(SE = 0.063\)
considering question b
The sample size is n = 500
The proportion of US adults are college graduates is p = 0.275
Generally the center is equivalent to the proportion so the center is 0.275
Generally the standard error is
\(SE = \sqrt{\frac{p * (1- p)}{ n} }\)
=> \(SE = \sqrt{\frac{0.275 * (1- 0.275)}{ 500} }\)
=> \(SE = 0.020\)

In the sampling distribution, the center of the sampling distribution is 0.275 and the standard error is 0.063.
What is sampling distribution?A sampling distribution simply means the probability distribution that is gotten from a larger number of samples that are drawn from a population.
In this case, the center of the sampling distribution is 0.275 and the standard error is 0.063. The standard error will be:
= [p × (1 - p)]/n
= [0.275 × (1 - 0.275)]/50
= 0.0039875
= ✓0.0039875
= 0.063
Also, when the sample is 500, the center of the sampling distribution is 0.275 and the standard error is 0.020.
Learn more about sampling distribution on:
https://brainly.com/question/15205225
¿De qué número 64 es el 80%?
Answers
PLEASE HELP!!! due today!!

Answers
Answer:
The maximum distance between supports for the beam to support a weight of 1600 lb is also 4.5 feet.
Step-by-step explanation:
We are given that weight P is inversely proportional to the distance D between the supports of the beam, and for this certain type of wooden beam, we have:
P = 7200/D
To find the distance between supports needed to carry 1600 lb, we can substitute P = 1600 in the above equation and solve for D:
1600 = 7200/D
D = 7200/1600
D = 4.5 feet
So the distance between supports needed to carry 1600 lb is 4.5 feet.
To find the maximum distance between supports for the beam to support a weight of 1600 lb, we can use the same equation and solve for P = 1600:
1600 = 7200/D
D = 7200/1600
D = 4.5 feet
Therefore, the maximum distance between supports for the beam to support a weight of 1600 lb is also 4.5 feet.
Which of the following is the equation of the function f(x) graphed above? A. ƒ(x) = x(x − 2)²(x − 1)(x + 1) B. f(x) = (x - 2) (x − 1)(x + 1) c. f(x)= x(x - 2)²(x − 1)(x + 1) + 1)² D. f(x) = (x - 2)²(x - 1)(x - 1)^ E

Answers
Calculate the sector area: 16 in 90°
Answers
Therefore , the solution of the given problem of area comes out to be
r = 8.
Define area.The term "area" describes the amount of space occupied by a 2D form or surface. We use cm2 or m2 as our units for measuring area. A shape's area is determined by dividing its length by its breadth.
Here,
A 90 degree sector occupies 1/4 of a circle, which has 360 degrees. Consequently, the area of the whole circle can be written as
Sector Size/Sector Area = Circle Area/360
16 ft2/90 = n/360
(360) (16 ft2)/90 = n
(4)(16 ft2) = n
The total size of the circle is n = 64 ft2.
Since Area of a Circle equals r2,
∏r2 = 64
r2 = 64/∏
r = √(64/∏)
We multiply by / to get by rationalizing the denominator.
r = √(64∏)/√(∏2) Then using the denominator's square root, we can obtain the solution of
r = √(64∏)/∏
r = 8
Therefore , the solution of the given problem of area comes out to be
r = 8.
To know more about area, visit
https://brainly.com/question/27683633
#SPJ1
can you answer the question please

Answers
Answer:
(x-5,y-1) traslation
Step-by-step explanation:
Hope this helps!❆
Trigonometry: Measure tal Excel In Opt. Mathematics - Book 9 ) If the number of degrees of a certain angle added to the number of gra same angle is 152, find the angle in degrees.
Answers
The angle in degrees is 873.1843.
Let the measure of the angle be θ in degrees. Therefore, the measure of the same angle in gradians is (θ × π/180).
According to the given information, the number of degrees of a certain angle added to the number of gradians of the same angle is 152.(θ) + (θ × π/180) = 152.
Simplifying the above equation, we get:(θ) + (θ/180 × π) = 152.
Multiplying both sides of the equation by 180/π, we get:
θ + θ = (152 × 180)/π2θ = (152 × 180)/πθ = (152 × 180)/(3.14)θ = 873.1843
Thus, the angle in degrees is 873.1843.
For more such questions on angle, click on:
https://brainly.com/question/25770607
#SPJ8
MATH PERIMETER HELP PLS
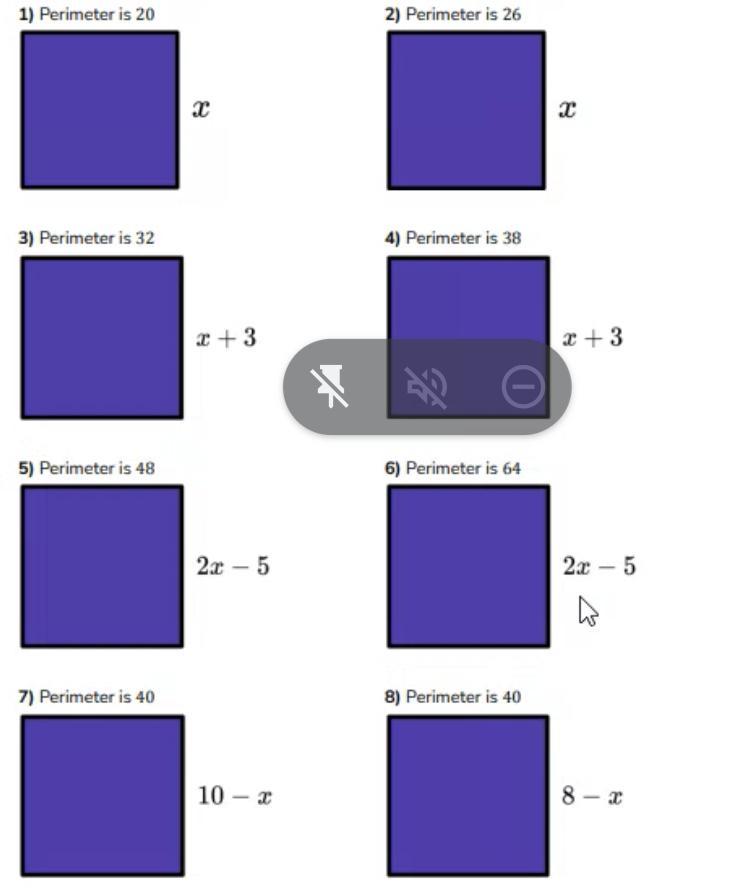
Answers
The value of x in each of the case is given below.
What is Perimeter?Perimeter of a straight sided figures or objects is the total length of it's boundary.
The given figures are squares.
Perimeter of a square is the sum of the length of four sides. Since all the sides are equal,
Perimeter of square = 4s, where s is the length of a side
1. Length of one side is x and the perimeter is 20.
4x = 20
x = 20 / 4 = 5
2. Length of one side is x and the perimeter is 26.
4x = 26
x = 26 / 4 = 6.5
3. 4(x + 3) = 32
4x + 12 = 32
4x = 20
x = 20 / 4 = 5
Length of a side = x + 3 = 8
4. 4(x + 3) = 38
4x + 12 = 38
4x = 26
x = 26 / 4 = 6.5
Length of a side = x + 3 = 9.5
5. 4 (2x - 5) = 48
8x - 20 = 48
8x = 68
x = 68 / 8 = 8.5
Length of one side = 2x - 5 = (2 × 8.5) - 5 = 12
6. 4 (2x - 5) = 64
8x - 20 = 64
8x = 84
x = 84 / 8 = 10.5
Length of a side = 2x - 5 = (2 × 10.5) - 5 = 16
7. 4 (10 - x) = 40
40 - 4x = 40
4x = 0
x = 0
Length of one side = 10 - x = 10 - 0 = 10
8. 4(8 - x) = 40
32 - 4x = 40
4x = -8
x = -2
Length of a side = 8 - -2 = 10
Hence the values of x and side lengths are found.
Learn more about Perimeters here :
https://brainly.com/question/30252651
#SPJ1
Translate the sentence into an equation.
The product of 4 and the sum of a number and 12 is 52.
The equation is
(Type an equation using x as the variable.)
Answers
Answer: 4*(x+12)=52.
The ratio of red starburst to yellow starburst in the bag is 8 to 3. There are 40 red starburst in the bag, how many are yellow?
Answers
What is the y-coordinate of the point that divides the
directed line segment from J to k into a ratio of 2:3?
13
12+
11+
10
9
8
7+
v = ( my mom n Ilv2 – va) + ve
O 6
0-5
6+
05
5
07
5
4+
3+
1 27
Mi

Answers
Answer:
5
Step-by-step explanation:
took the test
The coordinates of the point that divides the line segment from J to K into a ratio of 2:3 are P(-5,7), and the y-coordinate is 7, the correct option is D.
What is the ratio?Ratio is described as the comparison of two quantities to determine how many times one obtains the other. The proportion can be expressed as a fraction or as a sign: between two integers.
We are given that;
Ratio= 2:3
Now,
Let the point we are looking for be denoted as P(x,y), and let the ratio be 2:3, which means that the distance from J to P is 2/5 times the distance from J to K.
Using the distance formula, we can find the distance between J and K as:
d = sqrt((x2-x1)^2 + (y2-y1)^2)
= sqrt((-8 - (-3))^2 + (11 - 1)^2)
= sqrt(25 + 100)
= sqrt(125)
The distance from J to P is 2/5 of the total distance, which is:
(2/5)d = (2/5)sqrt(125) = 2sqrt(5)
Using the ratio formula, we get:
x = (3* (-3) + 2 * (-8)) / (3+2) = -5
y = (31 + 211) / (3+2) = 7
Therefore, by the given ratio answer will be 7.
Learn more about the ratio here:
brainly.com/question/13419413
#SPJ7
somebody help with this

Answers
Answer:
-27
Step-by-step explanation:
5(-3)^3(5)^-1
5(-27)(1/5)
-135(1/5)
-135/5
-27
Hopes this helps please mark brainliest
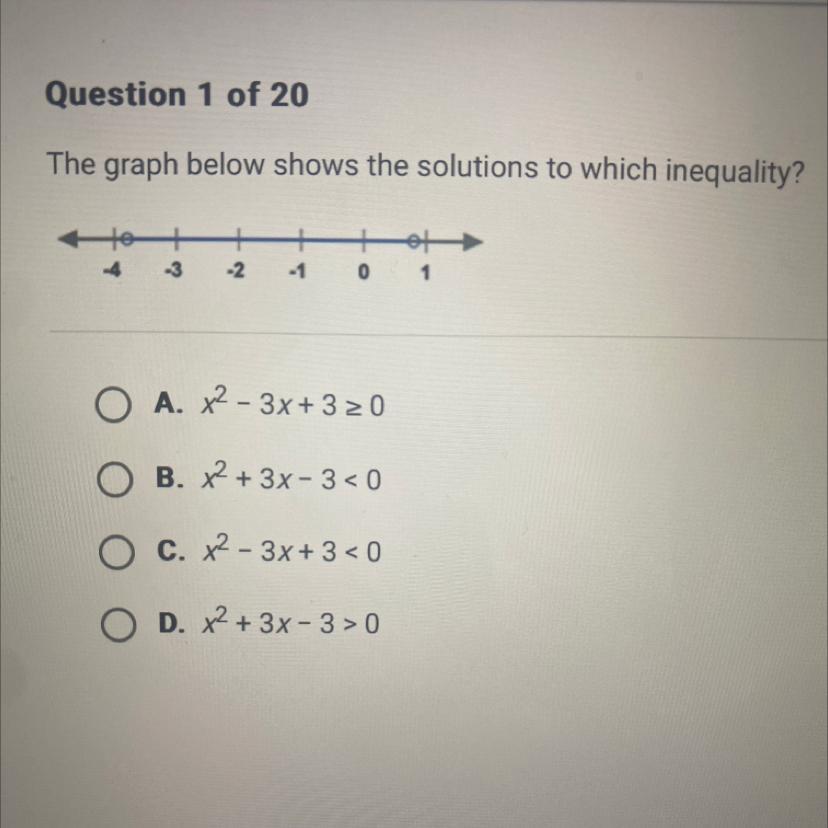
The graph below shows the solutions to which inequality?
A. x^2-3x+3 ≥0
B. x² + 3x-3 <0
C. x²-3x+3<0
D. x² + 3x-3>0
Answers
The inequality expression that corresponds to the solution of the inequality graph is x² + 3x - 3 < 0.
option B.
What is the solution of the inequality?The inequality expression that corresponds to the solution of the inequality graph is determined by simplifying the equations as follows;
The solution of the graph,
x > -4 and x < 1
The first equation with "≥" is ruled out because the graph doesn't have a thick dot.
Let's simplify the second expression;
x² + 3x - 3 < 0
solve using quadratic formula;
x > -3.79 or x < 0.79
The third expression is ruled out since its solution will be complex.
For the last expression;
x² + 3x - 3 > 0
x < -3.79 or x > 0.79
Thus, the correct inequality expression is x² + 3x - 3 < 0.
Learn more about inequality expression here: https://brainly.com/question/25275758
#SPJ1
NO LINKS!! URGENT HELP PLEASE!!
41. Sophie invested $5000 into an account that will increase in value by 2.3% each year. Write a function to model this situation, then find when will the account will have $15,000?
42. A baseball that was valued in 1980 has increased by 7% each year. Write a function to model this situation then find when the card will be worth $2000?
Answers
Answer:
41. 48 years and 3 months.
Step-by-step explanation:
41.
let's use the compound interest formula. The formula for compound interest is:
\(\bold{A = P * (1 + r)^n}\)
Where:
A is the final amount
P is the principal (initial investment)
r is the interest rate per period
n is the number of periods
we have,
P= $5000
A=$15000
r=2.3%
Now substituting value
\(15000=5000(1+\frac{2.3}{100})^n\\15000=5000(1.023)^n\\\frac{15000}{5000}=(1.023)^n\\3=(1.023)^n\)
doing logarithms of both sides of the equation.
We can use the natural logarithm (ln) to solve for n. The equation becomes:
\(ln(3) = ln(1.023)^n\)
Using the logarithmic property\(lna^b = b * ln(a),\) we can rewrite the equation as:
ln(3) = n * ln(1.023)
n=\(\frac{ln \:3}{ln\:1.023}\)
n=48.313 years approximately 48 years and 3 months.
Answer:
41. 49 years
42. 34 years and 12 days
Step-by-step explanation:
As the account increases by a constant percentage each year, we can use the exponential growth formula to write a function to model the situation.
\(\boxed{\begin{minipage}{8 cm}\underline{Exponential Growth Formula}\\\\$ f(t)=a\left(1+r\right)^{t}$\\\\where:\\\\ \phantom{ww}$\bullet$ $f(t)$ is the account balance. \\ \phantom{ww}$\bullet$ $a$ is the principal amount.\\ \phantom{ww}$\bullet$ $r$ is the interest rate (in decimal form). \\ \phantom{ww}$\bullet$ $t $ is the time (in years). \\ \end{minipage}}\)
Given values:
f(t) = $15,000a = $5,000r = 2.3% = 0.023Substitute the given values into the formula, and solve for t:
\(\begin{aligned}f(t)&=a(1+r)^t\\\\\implies 15000&=5000(1+0.023)^t\\15000&=5000(1.023)^t\\3&=(1.023)^t\\\\\textsf{Take natural logs:} \quad \ln (3)&=\ln (1.023)^t\\\ln (3)&=t\ln (1.023)\\t&=\dfrac{\ln (3)}{\ln (1.023)}\\t&=48.3129760...\end{aligned}\)
The account balance will reach $15,000 during the 48th year. As the interest is applied annually, we need to round up to the nearest whole year. Therefore, the account balance will reach $15,000 after 49 years.
Note: At the end of 48 years, the account balance will be $14,893.63, and after 49 years it will be $15,236.18.
\(\hrulefill\)
As the baseball's value increases by a constant percentage each year, we can use the exponential growth formula to write a function to model the situation.
\(\boxed{\begin{minipage}{8 cm}\underline{Exponential Growth Formula}\\\\$ V(t)=a\left(1+r\right)^{t}$\\\\where:\\\\ \phantom{ww}$\bullet$ $V(t)$ is the value of the baseball card. \\ \phantom{ww}$\bullet$ $a$ is the initial value of the card in 1980.\\ \phantom{ww}$\bullet$ $r$ is the interest rate (in decimal form). \\ \phantom{ww}$\bullet$ $t $ is the time (in years). \\ \end{minipage}}\)
Given values:
V(t) = $2,000a = $200r = 7% = 0.07Substitute the given values into the formula, and solve for t:
\(\begin{aligned}V(t)&=a(1+r)^t\\\\\implies 2000&=200(1+0.07)^t\\2000&=200(1.07)^t\\10&=(1.07)^t\\\\\textsf{Take natural logs:} \quad \ln (10)&=\ln (1.07)^t\\\ln (10)&=t\ln (1.07)\\t&=\dfrac{\ln (10)}{\ln (1.07)}\\t&=34.0323838...\end{aligned}\)
The value of the baseball card will reach $2,000 during the 34th year - after 34 years and 12 days. As this is not an investment account where interest is applied annually, we don't need to round up. Therefore, the baseball card will be worth $2,000 after 34 years and 12 days.
Helpp me please find the angle (where the question mark is ) 10 pointsss

Answers
Answer:
#9= 100 degrees but I'm not sure about #10.
Step-by-step explanation:
We know that a triangle has a total of 180 degrees.
So we add 16, 34, and 30
16+34+30=80
Then we subtract the amount from the total degrees of a triangle.
180-80
= 100 degrees
I hope this helps:)
The length of a rectangle is 3m less than double the witch, and the area of the rectangle is 27m^2. Find the dimensions of the rectangle.
Answers
Answer:
the area of the rectangle is A=L•W
The length is 3m less than twice its width W: L+ 3m=2W...->, L=2W-3m
A=L-W
27m²=(2W-3m)-W
27m2=2w2-3m-W
2w2-3wm-27m2=0
....use quadratic formula -(-3m)+ (-3m)²-4-2-(-27m²)
W=
2-2
w=(3m± √9m²+216m²)
w=(3m+ √225m²)
W=(3m± 15m...you need only positive root because width cannot be negative
W= 3m+15m
4
W=. 4
18m
W=4.5m ......now find the L
L=2.4.5m-3m
L=9m-3m
L=6m
Answer:
W = 4.5cm
L = 6cm
Step-by-step explanation:
what are the two integers that the square root of 108 fall between
Answers
It can be observed that number 108 lie between 100 and 121, two numbers which are perfect square.
So square root of 108 fall between square root of 100 and square root of 121.
Determine the square root of 100 and 121.
\(\sqrt[]{100}=10\)\(\sqrt[]{121}=11\)So square root of 108 fall between two integers 10 and 11.
Gas prices are up 30% since last year when they were $4.35, how much is gas now?
Answers
Answer:
given;
previous year price of gas= $4.35
price of gas has been increased by 30%
now,price of gas in present year=?
we have;
price of gas in present year=priceof
previous year+30%of price of previous year.
so ,price of gas in present year=4.35+30%of4.35
=$4.35+30/100×4.35
=$4.35+1.305
= $5.655. ans....
therefore, the price of gas in present year is ;$5.655.
give me yellow colour free fire
Answers
Answer:
okHow big of fire
Step-by-step explanation:
Answer:
Step-by-step explanation:
Dissolving in rubbing alcohol (like 70% alcohol) works much better because it contains enough water to dissolve the compound, but alcohol to help the fire. Then, you can mix the dissolved salt with any liquid fuel. Alternatively, use a spray bottle to spritz a blue flame to turn it yellow.
What percent of 2 is 32? If necessary, round your answer to the nearest tenth.
Answers
Answer:
Below
Step-by-step explanation:
32/2 x 100% = 1600 %
What is a 90% confidence interval for the true proportion of adult drivers who have often or sometimes talk on a cell phone when driving
Answers
The question is incomplete. Here is the complete question.
USA Today reported that 36% of adult drivers admit that they often or sometimes talk on a cell phone when driving. This was based on a random sample of 1004 adult drivers.
a) What is a 90% confidence interval for the true proportion of adult drivers who have often or sometimes talk on a cell phone when driving?
b) What is a 95% confidence interval for the true proportion of adult drivers who have often or sometimes talk on a cell phone when driving?
c) What is a 99% confidence interval for the true proportion of adult drivers who have often or sometimes talk on a cell phone when driving?
d) What do you notice?
Answer and Step-by-step explanation: The way to calculate confidence interval for proportions is by using the following formula:
\(z(\sqrt{\frac{p(1-p)}{n} } )\)
where
p is the sample population proportion
n is the number of individuals in the sample
z is z-score associated of the % of confidence
a) A 90% confidence has a z-score of z = 1.645
Calculating:
Interval = \(1.645(\sqrt{\frac{0.36(1-0.36)}{1004} } )\)
Interval = \(1.645(\sqrt{0.00023} )\)
Interval = \(1.645(0.01515)\)
Interval = 0.025
A 90% Confidence interval for true population is between 0.335 and 0.385.
b) A 95% confidence has a z-score of z = 1.96
Since the sample parameter didn't change, the interval will be:
Interval = 1.96(0.01515)
Interval = 0.03
For a 95% confidence, interval is between 0.33 and 0.39.
c) A 99% confidence has a z-score of z = 2.58
Interval = 2.58(0.01515)
Interval = 0.39
For a 99% confidence, interval is between -0.03 and 0.75
d) Confidence interval tells you how certain your results from polling or survey would represent the real population's behaviour. In the experiment above, as the percentage of certainty grows, closer the real population proportion actually is for adult drivers who often or sometimes talk on a cell phone when driving.
find net price (show work)
25% discount on $225 purchase.
Answers
Answer:
$191.25
Step-by-step explanation:
multiply 255 dollars by 25 percent, and then divide the answer by one hundred, then deduct that result from the original price.
(255 x 25)/100 = $63.75
255 - 63.75 = $191.25