The table shows prices that three different people paid for the same kind of fresh salmon at Fiona’s Fish Factory.
Explain why this is a proportional relationship.

Answers
The relationship is proportional because the price for one pound of fresh salmon is the same for the different price paid.
Why is the relationship proportional?If the relationship is proportional, the cost of one pound of fresh salmon for all the three options would be the same.
$29.25 / 3 = $9.75$48.75 / 5 = $9.75$78 / 8 = $9.75To learn more about division, please check: https://brainly.com/question/132812067
#SPJ1
Related Questions
Choose the sentence with correctly placed commas.
Question 2 options:
A. New students, experience social stress to say the least, on top of the stress of change.
B. New students experience social stress, to say the least, on top of the stress of change.
C. New students experience social stress, to say the least on top of the stress of change.
D. New students experience social stress to say the least, on top of the stress of change.
Answers
Answer:
Step-by-step explanation:
Option D
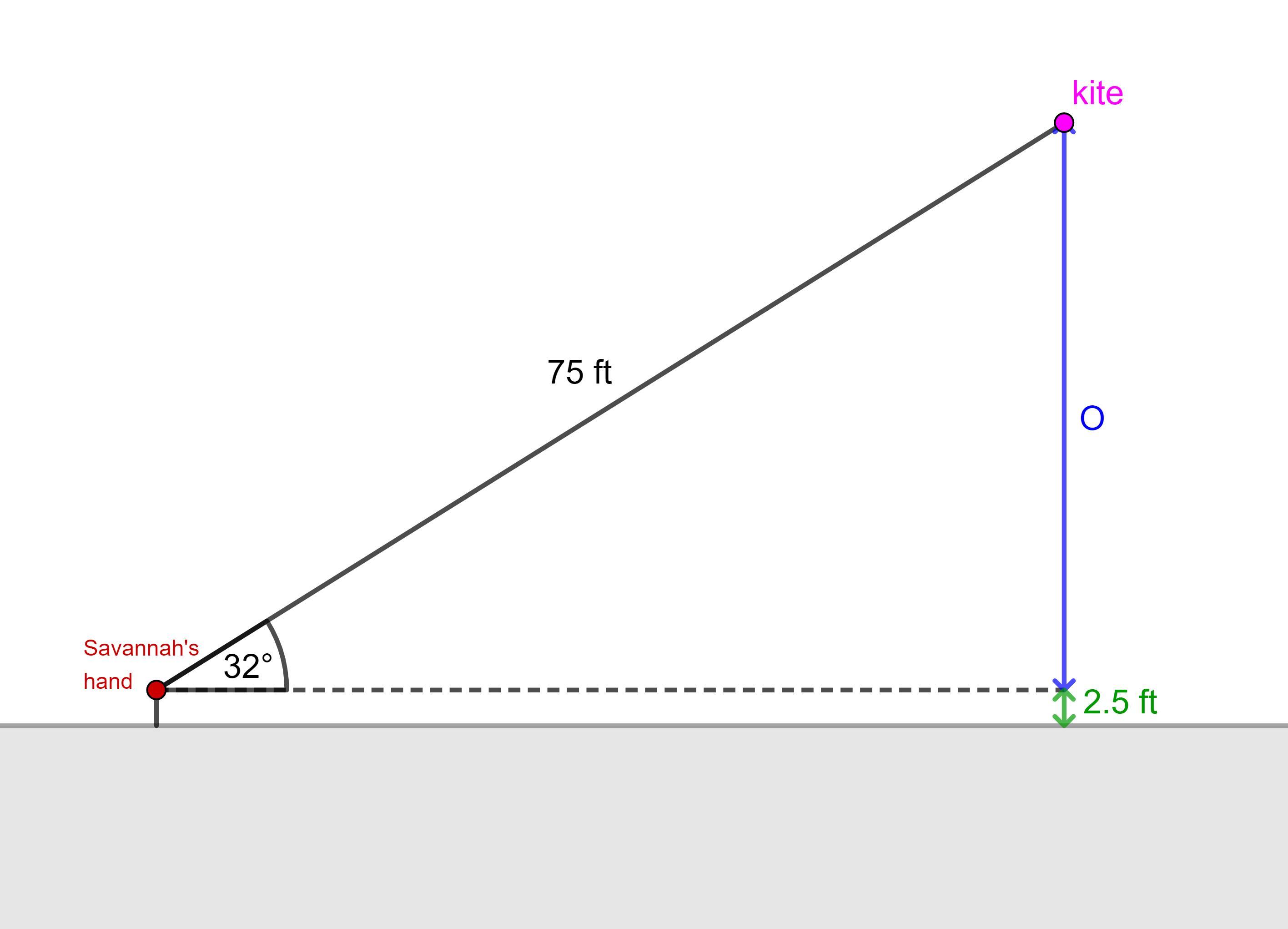
Savannah is flying a kite, holding her hands a distance of 2.5 feet above the ground
and letting all the kite's string play out. She measures the angle of elevation from her
hand to the kite to be 32. If the string from the kite to her hand is 75 feet long, how
many feet is the kite above the ground? Round your answer to the nearest tenth of a
foot if necessary.
Answer:
feet Submit Prowes
Z
Answers
Answer:
42.2 ft
Step-by-step explanation:
The given scenario can be modelled as a right triangle (see attached diagram), where the angle of elevation is 32°, and the length of the kite string (75 ft) is the hypotenuse.
We want to find the distance the kite is above the ground, so we want to find the side of the right triangle that is opposite the given angle. To do this, we can use the sine trigonometric ratio.
\(\boxed{\begin{minipage}{9 cm}\underline{Sine trigonometric ratio} \\\\$\sf \sin(\theta)=\dfrac{O}{H}$\\\\where:\\ \phantom{ww}$\bullet$ $\theta$ is the angle. \\ \phantom{ww}$\bullet$ $\sf O$ is the side opposite the angle. \\\phantom{ww}$\bullet$ $\sf H$ is the hypotenuse (the side opposite the right angle). \\\end{minipage}}\)
Substituting θ = 32° and H = 75 into the ratio, we get:
\(\sin 32^{\circ}=\dfrac{\sf O}{75}\)
\(\textsf{O}=75\sin 32^{\circ}\)
\(\textsf{O}=39.7439448...\; \sf ft\)
The angle of elevation is the angle between the horizontal plane and the line of sight from an observer to an object located at a higher position.
In this scenario, the angle of elevation is measured from Savannah's hand, which is a distance of 2.5 ft above the ground. Therefore, we need to add 2.5 ft to the value of O found using the sine ratio.
\(\implies 39.7439448...+2.5=42.2\; \sf ft\;(nearest\;tenth)\)
Therefore, the kite is 42.2 ft above the ground (rounded to the nearest tenth).
Question on pic thx!

Answers
Answer:
17 hours
Step-by-step explanation:
This question can be solved using a proportion, without the need to actually find the unit rate.
hours/dollars = x/357 = 11/231
x = 357(11/231) = 17 . . . . . multiply by 357
He would have to work 17 hours to make $357.
Answers to these 3 questions ?

Answers
60 = 6y
10 = y
8(10) + 36
80 + 36
116
116° for the top and bottom angles
48 + x = 64
x = 16
64° is the measurements for the horizontal angles
44. 11.22(2) = 22.44
TE = 22.44
45. 4x + 8 + 27 = 6x
35 = 2x
17.5 = x
4(17.5) + 8
70 + 8
CD = 78
6(17.5)
CE = 105
Jeff has 8 red marbles 6 blue marbles, and 4 green marbles that are the same size and shape he puts the marbles into a bag, mixes the marbles and randomly picks one Marble. What is the probability that the marble will be blue
Answers
Hey buddy I am here to help!
Red = 8
blue = 6
greem = 4
total = 18
probability of blue marble = 6/18 = 1/3
Answer:
I think it is 1/3
Step-by-step explanation:
you have 18 ways to pick one marble in the bag and have 6 ways to pick a blue marble so the probability that the marble will be blue is 6/18=1/3
Please, help me find the answer

Answers
The probability values for the questions posed are :
11/20probability of Public speaking given that student is majoring in Business Administration1/3A.)
Number of students Taking a public speaking class majoring in business administration.
10 + 45 = 55P(PS or BA) = 55/100 = 11/20
Therefore, the probability of PS or BA is 11/20
B.)
For the survey described, P(taken a public speaking class | majoring in Business Administration) represents the probability that a selected student has taken a public speaking class given that the student is majoring in business administration.
Hence, as inferred from P(A|B) ; probability of A given B.
C.)
P(PS|BA) = n(PSnBA) / n(BA)
n(PS) = 10+20 = 30
n(PSnBA) = 10
P(PS|BA) = 10/30 = 1/3
Therefore , the probability of PS|BA is 1/3.
Learn more on probability:https://brainly.com/question/24756209
#SPJ1
find the approximate area of the shaded region, given that the area of the sector is approximately 13.08 square units.

Answers
The area of the shaded region is 3915 units².
We have,
Area of the sector.
= 13.08 units²
Now,
To find the area of an isosceles triangle with side lengths 5, 5, and 4 units, we can use Heron's formula.
Area = √[s(s - a)(s - b)(s - c)]
where s is the semi-perimeter of the triangle, calculated as:
s = (a + b + c) / 2
In this case,
The side lengths are a = 5, b = 5, and c = 4. Let's calculate the area step by step:
Calculate the semi-perimeter:
s = (5 + 5 + 4) / 2 = 14 / 2 = 7 units
Use Heron's formula to find the area:
Area = √[7(7 - 5)(7 - 5)(7 - 4)]
= √[7(2)(2)(3)]
= √[84]
≈ 9.165 units (rounded to three decimal places)
Now,
Area of the shaded region.
= Area of the sector - Area of the isosceles triangle
= 13.08 - 9.165
= 3.915 units²
Thus,
The area of the shaded region is 3915 units².
Learn more about Circle here:
https://brainly.com/question/11833983
#SPJ1
Evaluate the double integral ∬R(3x−y)dA, where R is the region in the first quadrant enclosed by the circle x2+y2=16 and the lines x=0 and y=x, by changing to polar coordinates.
Answers
Answer:
\(\displaystyle 64-32\sqrt{2}+\frac{32\sqrt{2}}{3}\approx3.66\)
Step-by-step explanation:
\(\displaystyle \iint_R(3x-y)\,dA\\\\=\int^\frac{\pi}{2}_\frac{\pi}{4}\int^4_0(3r\cos\theta-r\sin\theta)\,r\,dr\,d\theta\\\\=\int^\frac{\pi}{2}_\frac{\pi}{4}\int^4_0(3r^2\cos\theta-r^2\sin\theta)\,dr\,d\theta\\\\=\int^\frac{\pi}{2}_\frac{\pi}{4}\int^4_0r^2(3\cos\theta-\sin\theta)\,dr\,d\theta\\\\=\int^\frac{\pi}{2}_\frac{\pi}{4}\frac{64}{3}(3\cos\theta-\sin\theta)\,d\theta\\\\=\int^\frac{\pi}{2}_\frac{\pi}{4}\biggr(64\cos\theta-\frac{64}{3}\sin\theta\biggr)\,d\theta\)
\(\displaystyle =\biggr(64\sin\theta+\frac{64}{3}\cos\theta\biggr)\biggr|^\frac{\pi}{2}_\frac{\pi}{4}\\\\=\biggr(64\sin\frac{\pi}{2}+\frac{64}{3}\cos\frac{\pi}{2}\biggr)-\biggr(64\sin\frac{\pi}{4}+\frac{64}{3}\cos\frac{\pi}{4}\biggr)\\\\=64-\biggr(64\cdot{\frac{\sqrt{2}}{2}}+\frac{64}{3}\cdot{\frac{\sqrt{2}}{2}}\biggr)\\\\=64-32\sqrt{2}+\frac{32\sqrt{2}}{3}\biggr\\\\\approx3.66\)
A system of equations is given.
Equation 1: 4x − 6y = 10
Equation 2: 9x + 2y = 7
Explain how to eliminate x in the system of equations.
Answers
Step-by-step explanation:
To eliminate x in the system of equations:
1. Multiply Equation 1 by 9 and multiply Equation 2 by -4, this gives:
Equation 1: 36x -54y = 90
Equation 2: -36x - 8y = -28
2. Add the two equations together to eliminate x:
(36x - 54y) + (-36x - 8y) = 90 - 28
Simplifying, we get:
-62y = 62
3. Solve for y:
y = -1
4. Substitute y = -1 into one of the original equations, say Equation 1:
4x - 6(-1) = 10
Simplifying, we get:
4x + 6 = 10
5. Solve for x:
4x = 4
x = 1
Therefore, the solution to the system of equations is x = 1 and y = -1. We can check that these values are correct by substituting them back into the original equations and verifying that they satisfy both equations.
going to send you a pic of my question
Answers
We know that we can have
0, 1, 2,... pencils
This mean that we cannot have a negative number of pencils (that would not have sense)
Then choice C and D are discarded
Since we can have 8 or less and we could have 0 pencils then the options are
0, 1, 2, 3, 4, 5, 6, 7 or 8
Answer: Ashow how to find slope of a line that passes through the points in the table
Answers
Answer:
Step-by-step explanation:
here you go m = (y2-y1)/(x2-x1)
= (11-(-9))/(3-(-1))
= 20/4
= 5
Unions, intersections, and complements involving 2 sets
Sets B and C are subsets of the universal set U.
These sets are defined as follows.
U={f, k, m, s, x, y, z)
B={k, s, y}'
C={s,z}
(a) B'UC' = 1
(b) B'nc =
Answers
Intersection of B'∩C = {k, y}
To find the intersection of B' and C, we need to first find the complement of set B (B') and then find the intersection between B' and C.
1. Complement of set B (B'):
The complement of set B (B') consists of all elements in the universal set U that are not in set B. From the given information, set B is defined as {k, s, y}', which means it contains all elements in U except for k, s, and y. Therefore, the complement of set B is {f, m, x, z}.
2. Intersection between B' and C:
Now, we need to find the intersection between B' (complement of B) and set C. From the given information, set C is defined as {s, z}. To find the intersection, we need to identify the common elements between B' and C.
The elements present in both B' and C are k and y. Therefore, the intersection of B' and C is {k, y}.
So, the answer to (b) is B'∩C = {k, y}.
For more such questions on Intersection, click on:
https://brainly.com/question/30915785
#SPJ8
In a right-angled triangle the ratio of the two smaller angles is 3:2. Find the sizes of each of the angles.
Answers
Answer:
36° , 54° , 90°
Step-by-step explanation:
since the triangle is right then one angle is 90°
the ratio of the smaller angles = 3 : 2 = 3x : 2x ( x is a multiplier )
the sum of the 3 angles in the triangle is 180° , that is
3x + 2x + 90 = 180
5x + 90 = 180 ( subtract 90 from both sides )
5x = 90 ( divide both sides by 5 )
x = 18
Then
3x = 3 × 18 = 54°
2x = 2 × 18 = 36°
the 3 angles measure 36° , 54° , 90°
Evaluate the expression, given functions f and g: f(x) = 3x – 2, g(x) = 7 – x2.
3f(1) - 49(-2)
Answers
f(x) = 3x – 2, g(x) = 7 – x2.
3f(1) - 49(-2)
Substitute the given value into the function and evaluate.
101
The value of 3f(1) - 49(-2) for the given function f(x) = 3x – 2 will be 101.
What is a function?A certain kind of relationship called a function binds inputs to essentially one output.
A function can be regarded as a computer, which is helpful.
The machine will only accept specified inputs, described as the function's domain, and will potentially produce one output for each input.
Given the function,
f(x) = 3x – 2
Now,
f(1) = 3(1) - 2 = 1
So,
3f(1) - 49(-2) = 3×1 - 49(-2)
⇒ 3 + 98 = 101
Hence "The value of 3f(1) - 49(-2) for the given function f(x) = 3x – 2 will be 101".
For more about the function,
brainly.com/question/23712366
#SPJ2
Find the slope of the line that goes through the given points. 1) (3, -5), (7,-6)
Answers
Answer:
slope = - \(\frac{1}{4}\)
Step-by-step explanation:
Calculate the slope m using the slope formula
m = \(\frac{y_{2}-y_{1} }{x_{2}-x_{1} }\)
with (x₁, y₁ ) = (3, - 5) and (x₂, y₂ ) = (7, - 6)
m = \(\frac{-6-(-5)}{7-3}\) = \(\frac{-6+5}{4}\) = - \(\frac{1}{4}\)
mations to Determine Similarity
What steps would you take to determine if these
figures are similar? Check all that apply.
Use a scale factor of 2.
Multiply the vertices of polygon ABCD by
O Translate the intermediate image 4 units down.
Perform two different dilations.
Reflect the intermediate image.
Answers
The steps which you would take to determine if these figures are similar include the following:
2. Multiply the vertices of polygon ABCD by 1/2.
5. Reflect the intermediate image.
What is a dilation?In Mathematics and Geometry, a dilation is a type of transformation which typically transforms the dimension (size) or side lengths of a geometric object, without affecting its shape.
Therefore, the dimension or side lengths of the dilated geometric object would be stretched or compressed (shrunk) depending on the scale factor that is applied.
By critically observing the graph representing polygon ABCD, we can logically deduce that a sequence of transformations that would polygon ABCD (pre-image) onto polygon A"B"C"D" (image) is a dilation by a scale factor of 1/2 and a reflection of intermediate image.
Read more on dilation and scale factor here: brainly.com/question/4421026
#SPJ1
Missing information:
The question is incomplete and the complete question is shown in the attached picture.

Measure the diameter of the tin in mm and write down the real diameter in mm
Answers
The required real diameter of the tin is 250 mm.
What is the diameter?Diameter is the length of a straight line drawn through the center of a circular object, such as a circle or sphere. It is the distance between two locations on the object's edge that are furthest apart and pass through the object's center.
Here,
If the diameter of the tin in the picture is 10 cm, then the actual diameter of the tin can be calculated as:
Actual Diameter = 2.5 x Picture DiameterActual Diameter = 2.5 x 10 cmActual Diameter = 25 cmTo convert the actual diameter to millimeters (mm), we can multiply by 10:
Actual Diameter in mm = Actual Diameter x 10Actual Diameter in mm = 25 cm x 10Actual Diameter in mm = 250 mmTherefore, the real diameter of the tin is 250 mm.
Learn more about diameter here:
brainly.com/question/5501950
#SPJ1
Full Question:
See the attached.

Write the solution set of the given homogeneous system in parametric vector form. x1 + 2x2-15x3 = 0 2x1 + x2-15x3-0 X1X2 where the solution set is x = | x2 X3 x=x3 (Type an integer or simplified fraction for each matrix element.
Answers
The solution set of the given homogeneous system in parametric vector form is x₁ = 5 = x₂ , x₃ = 1.
What is parametric vector form?
The identity matrix's two columns, which stand in for the two leading coefficients in the row echelon form of the original matrix, are added to create the parametric vector.
We are given set of equations as:
x₁ + 2x₂ - 15x₃ = 0
2x₁ + x₂ - 15x₃ = 0
-x₁ + x₂ = 0
Now, representing this in the matrix form, we get
\(\left[\begin{array}{cccc}1&2&-15&0\\2&1&-15&0\\-1&1&0&0\end{array}\right]\)
Now, we will reduce the matrix i.e. in row echelon form using elementary operations
From this, we get
\(\left[\begin{array}{cccc}1&0&-5&0\\0&1&-5&0\\0&0&0&0\end{array}\right]\)
So, we get that x₃ is the free variable.
Now, representing this in the parametric vector form, we get
x₁ - 5x₃ = 0
x₂ - 5x₃ = 0
x₃ = x₃
From this, we get
x₁ = 5x₃
x₂ = 5x₃
x₃ = x₃
So, we now get
x = \(\left[\begin{array}{c}x_{1} &x_{2} &x_{3} \end{array}\right]\)
This is equal to
x = \(\left[\begin{array}{c}5x_{3} &5x_{3} &x_{3} \end{array}\right]\)
Thus,
x = \(\left[\begin{array}{c}5 &5 &1 \end{array}\right]\)
Hence, the solution is x₁ = 5 = x₂ , x₃ = 1.
Learn more about parametric vector form from the given link
https://brainly.com/question/30465719
#SPJ4
David's brother wants him to
build a pool deck which will
take 8 days to complete. His
brother will pay him in one of
two ways. David can earn $70
a day or start with $3 for the
first day and double his pay
each day plus $3. Which
payment method should David
select?
Answers
what is the prevention of corruption finish give my answer to me
.
3+6+9+12+15+18+22+25=110
1st choice
Graph the following function:
f(x) = x² +5x - 6
What are the x-intercepts?
What is the y-intercept?
What is the maximum or minimum value?
Answers
Answer:
x-intercept(s): (1,0),(-6,0)
y-intercept: (0,-6)
I am not sure about the maximum and minimum value sorry
The movie ended at 7:05 p.m. and lasted 2 hours 40 minutes. What time did the movie begin?
Answers
Answer:
4 : 25pm
Step-by-step explanation:
If the movie ended at 7:05p.m, and the movie is as long as 2 hours 40 minutes, therefore the starting time is 2 hours 40 minutes earlier than the ending time
Therefore
7:05 - 2 hours and 40 minutes
= 4 : 25pm
i need help with this aswell, i dont understand them :(

Answers
Answer:
4 and 9
Step-by-step explanation:
I am going to use an upper case E for the symbol in the answers. The E symbol means "is a member of set..."
So " 1 E A " means "1 is a member of set A."
And " 4 E A" means "4 is a member of set A.
Now at the beginning of the question they told you what numbers were in which sets. 1 through 9 are in set U. But only 4 and 9 are in set A. The contents of the set are listed in between a pair of grouping symbols { } that are kind of squiggly brackets. That's how you know what is in the set.
Since set A only contains 4 and 9, those are your two correct answers:
"4 E A" AND "9 E A"
9 decreased by 3 times a number translated in algebra form
Answers
9 - 3 x n
decreased is subtraction and 3 times is multiplication
Are the two triangles above similar? Why or why not?
A. Yes, they are similar by the AA similarity postulate.
B. Yes, they are similar by the SAS similarity theorem.
C. No, two congruent angles is not enough information to prove similarity.
D. No, triangles with two congruent angles are never similar.

Answers
Answer:
is it c??
Step-by-step explanation:
Answer:
A
Step-by-step explanation:
Because of the dashes on the angles, angle A is congruent to angle D and angle B is congruent to angle E. Since we know that 2 angles are congruent, the triangles are similar because of AA similarity
Alicia borrow 15000 to buy a car she borrowed the money at 8% for 6 years how much will she have to pay the bank at the end of 6 years
Answers
Answer:
Explanation:
First, we identify the main components:
• Principal = $15,000
,• Rate = 8% =0.08
,• Time = 6 years
\(undefined\)The vertices of a polygon are L(2,4) M (2,7) N (8,7) O (8,4) P(6 0), and Q(4,0)Graph the polygon. Then
find its area
Answers
According to the information, we can infer that the area of this polygon is 34 units².
How to find the area of the figure?To find the area of the figure we must graph it and divide it into different segments. Then we find the area of all the segments and add them to get the total area.
Rectangle 1
6 * 3 = 18
Rectangle 2
2*4=8
Triangle 1
2 * 4 / 2 = 4
Triangle 2
2 * 4 / 2 = 4
Total Area
18 + 8 + 4 + 4 = 34
Based on the above, we can infer that the total area of the polygon is 34 ² units.
Learn more about polygons in: https://brainly.com/question/24464711
#SPJ1

The tensile strength of a metal part is normally distributed with mean 40 pounds and standard deviation 5 pounds. If 50,000 parts are produced, how many would you expect to fail to meet a minimum specification limit of 35-pounds tensile strength? How many would have a tensile strength in excess of 48 pounds?
Answers
Answer:
a) how many would you expect to fail to meet a minimum specification limit of 35-pounds tensile strength?
7933 parts
b) How many would have a tensile strength in excess of 48 pounds?
2739.95 parts
Step-by-step explanation:
The formula for calculating a z-score is is z = (x-μ)/σ, where x is the raw score, μ is the population mean, and σ is the population standard deviation.
a) how many would you expect to fail to meet a minimum specification limit of 35-pounds tensile strength?
z = (x-μ)/σ
x = 35 μ = 40 , σ = 5
z = 35 - 40/5
= -5/-5
= -1
Determining the Probability value from Z-Table:
P(x<35) = 0.15866
Converting to percentage = 15.866%
We are asked how many will fail to meet this specification
We have 50,000 parts
Hence,
15.866% of 50,000 parts will fail to meet the specification
= 15.866% of 50,000
= 7933 parts
Therefore, 7933 parts will fail to meet the specifications.
b) How many would have a tensile strength in excess of 48 pounds?
z = (x-μ)/σ
x = 48 μ = 40 , σ = 5
z = 48 - 40/5
z = 8/5
z = 1.6
P-value from Z-Table:
P(x<48) = 0.9452
P(x>48) = 1 - P(x<48)
1 - 0.9452
= 0.054799
Converting to percentage
= 5.4799%
Therefore, 5.4799% will have an excess of (or will be greater than) 48 pounds
We are asked, how many would have a tensile strength in excess of 48 pounds?
This would be 5.4799% of 50,000 parts
= 5.4799% × 50,000
= 2739.95
Therefore, 2739.95 parts will have a tensile strength excess of 48 pounds
9What is the sum of the geometric series 500 (1.05)*¹m=1?

Answers
Given:
The geometric series
\(\sum_{n\mathop{=}1}^9500(1.05)^{n-1}\)Required:
What is the sum of gemetric series?
Explanation:
The formula for sum of geometric series with finite terms:
\(\begin{gathered} S_n=\frac{a(r^n-1)}{r-1} \\ Where, \\ a(first\text{ }term) \\ r(common\text{ }ratio) \end{gathered}\)So, the series:
\(\begin{gathered} =500+500(1.05)+500(1.05)^2+...... \\ So,r=\frac{500(1.05)}{500} \\ r=1.05 \end{gathered}\)Now, sum is:
\(\begin{gathered} S_9=\frac{500(1.05^9-1)}{(9-1)} \\ =\frac{500(0.551)}{8} \\ =\frac{275.5}{8} \\ =34.4 \end{gathered}\)Answer:
The sum is 34.4
What is the image point of (-7,-8)after the transformation D1/2oT-1,0?
Answers
The image point of (-7,-8) after the transformation D1/2oT-1,0 is (-4,4).
First, we apply the translation T-1,0, which moves every point 1 unit to the right (since the x-coordinate is decreased by 1) and leaves the y-coordinate unchanged. Therefore, the image of (-7,-8) under T-1,0 is (-7-1,-8) = (-8,-8).
Next, we apply the dilation D1/2, which scales every distance from the origin by a factor of 1/2. Therefore, the image of (-8,-8) under D1/2 is (-8/2,-8/2) = (-4,-4).
Thus, the image point of (-7,-8) after the transformation D1/2oT-1,0 is (-4,4).
Learn more about transformation here:
https://brainly.com/question/30939258
#SPJ1
Given sin (-theta) = 1/5 and tan theta = sqrt.6/12
what is the value of cos theta?
- sqrt.6/60
2 sqrt.6/5
-2 sqrt.6/5
Sqrt.6/60
Answers
Given \(sin (\theta) = \frac{1}{5}\), and\(tan \theta = \frac{\sqrt{6} }{12}\), then:
\(cos\theta=\frac{2\sqrt{6} }{5}\)
Computations on trigonometric identitiesFrom the details provided:
\(sin (\theta) = \frac{1}{5}\ \\\\tan \theta = \frac{\sqrt{6} }{12} \times \frac{\sqrt{6} }{\sqrt{6} }\\\\tan \theta = \frac{\sqrt{6} \times \sqrt{6} }{12 \times \sqrt{6} }\\\\tan \theta =\frac{1}{2\sqrt{6} }\)
From the relationship above:
Opposite = 1
Adjacent = \(2\sqrt{6}\)
Hypotenuse = 5
\(cos\theta=\frac{Adjacent}{Hypotenuse} \\\\cos\theta=\frac{2\sqrt{6} }{5}\)
Learn more on trigonometry here: https://brainly.com/question/20519838