There are 25 Year 11 pupils in a tennis club, out of a total of 30 pupils.
Write this proportion as a percentage.
Give your answer correct to 1 decimal place when appropriate.
Answers
According to the solution we have come to find that, 83.3% of the pupils in the tennis club are in Year 11.
what is percentage?
Percentage is a way of expressing a number as a fraction of 100. It is often used to compare one quantity to another or to express how much of a particular quantity is present in a given situation. Percentages are denoted by the symbol "%". For example, if we say that a particular item is sold at a 25% discount, it means that the price of the item is reduced by 25% of its original value. Similarly, if we say that a particular student scored 80% on a test, it means that the student answered 80 out of 100 questions correctly. Percentages are commonly used in a variety of fields, including finance, economics, science, and education.
The proportion of Year 11 pupils in the tennis club is 25/30.
To convert this proportion to a percentage, we need to multiply it by 100:
(25/30) x 100 = 83.333...
Rounding this to one decimal place gives 83.3%.
Therefore, 83.3% of the pupils in the tennis club are in Year 11.
To learn more about percentages from the given link
https://brainly.com/question/29306119
#SPJ9
Related Questions
Consider the functions f(x) = 5x – 2, g(x) = 5x² + 2 and r(x) = –2x + 4.
Evaluate f(g(5)).
10 points!
Answers
Answer:
f(-2x+4) = -10x+18
Step-by-step explanation:
Answer:
733 I hope that helps! Sorry if its incorrect

I need help with four answers! Will mark brainliest : )!
Q.1:Which symbol replaces the box to make the statement true?
4⋅16−16□4⋅[24−2⋅(4+8)]
Q.2: Which expression has a value less than the given expression when x = 5?
3x + 15
-----------------------------------
Answers options:
2x²
x² + 5
3(x + 5)
4x + 5
Q.3:Let m = 4 and n = 5.
Select from the drop-down menu to create a true statement.
4m+4n = 2m2+
----------------------------
Answer options:
M
N
MN 2
Q.4: Which expression completes the statement to form a true equation?
28–3+2=
----------------------------------------------------
Answer options:
3³
5(4 + 2)
3² + 19
44–24
Answers
Answer:
Q1:=
Q2:4x+2
I believe question 3 is MN 2
3^3
ABC is an isosceles right triangle.
1). A = _____.
2). B = _____.
3). If AC = 3, then BC = _____ and AB = _____.
4). If BC = 4 then BC = _____ and AB = _____.
5). If BC = 9, then AB = ______.
6). If AB = 7 Square root 2, then BC = _____.
7). If AB = 2 square root 2, then AC = _____.

Answers
1) 45°
2) 45°
3) BC= 3 AB= sqrt(18)=3sqrt(2)
4) BC= 4 AB= sqrt(32)=4sqrt(2)
5) 9sqrt(2)
6) 7
7) 2
sqrt means square root
AC = AB because it is isosceles
pythagore theorem is used to solve 3 to 7
AB²= AC²+CB²
In 1 and 2 it is the angle in an isosceles triangle
A local grocery store receives strawberries from suppliers in Florida and California. Currently there are 18 strawberry containers on the shelf and 11 of them are from Florida. A shopper selects three containers to purchase. What is the probability that exactly one of the containers is from the Florida supplier
Answers
Using the hypergeometric distribution, it is found that there is a 0.2831 = 28.31% probability that exactly one of the containers is from the Florida supplier.
The containers are chosen without replacement, which means that the hypergeometric distribution is used to solve this question.
Hypergeometric distribution:
\(P(X = x) = h(x,N,n,k) = \frac{C_{k,x}C_{N-k,n-x}}{C_{N,n}}\)
\(C_{n,x} = \frac{n!}{x!(n-x)!}\)
The parameters are:
x is the number of successes. N is the size of the population. n is the size of the sample. k is the total number of desired outcomes.In this problem:
There are 18 containers, hence \(N = 18\)11 of those are in Florida, hence \(k = 11\).A sample of 3 containers is taken, hence \(n = 3\)The probability that exactly one of the containers is from the Florida supplier is P(X = 1), hence:
\(P(X = x) = h(x,N,n,k) = \frac{C_{k,x}C_{N-k,n-x}}{C_{N,n}}\)
\(P(X = 1) = h(1,18,3,11) = \frac{C_{11,1}C_{7,2}}{C_{18,3}} = 0.2831\)
0.2831 = 28.31% probability that exactly one of the containers is from the Florida supplier.
A similar problem is given at https://brainly.com/question/24826394
Hep me please i would really appreciate it

Answers
Answer:
Part A: 4,300 ≥ 2500 + 0.12s
Part B: Less than or equal to $15,000
Part C: In the image
Step-by-step explanation:
For Part A: The total needs to be at least 4,300. So 4,300 is greater than or equal to how much she earns. 2,500 is the base pay, and it is added to 0.12s, which represents 12% of sales (s).
For Part B:
Using the inequality, solve for s
4,300 ≥ 2500 + 0.12s
Subtract 2500 from both sides
1800 ≥ 0.12s
Now divide both sides by 0.12 to isolate s
15000 ≥ s
So sales must be less than or equal to 15000.
Part C:

what is
r+15=36
\(r + 15 = 36\)
Answers
Answer:
Step-by-step explanation:
R=21
state the domain of each function using interval notation
pls show ur work!!

Answers
Answer:
(-∞ , -6] ∪ [6 , +∞)
Step-by-step explanation:
Let D be the domain of f .
D = {x ∈ IR ; where x² - 36 ≥ 0}
x² - 36 ≥ 0
⇔ x² ≥ 36
⇔ x² ≥ 6²
⇔ √(x²) ≥ √(6²)
⇔ |x| ≥ 6
⇔ x ∈ (-∞ , -6] ∪ [6 , +∞)
If Bob deposits $133 at the end of every month in an account paying 5.9% interest compounded annually, how much money will he have in the account in 6 years? Round your final answer to the nearest cent (2 decimal places)
Answers
Answer:
10140.96 dollars
Step-by-step explanation:
Bob deposits 133 dollars at the end of every mounth in an account paying 5.9 percent interest compounded annually :
We need to khow what is the amount bob has in a total year without interests let A be the amount we are looking for : A = 12*133=1596 so bob has 1596 dollars each yearWe khow that the interest is worth 5.9 percent
we can state :
1596⇒ 100 percent x(the interest value)⇒ 5.9 percent x = (1596*5.9)/100 = 94.16 dollars each yearLet At be the toatl amount after six years
At= 1596*6+94.16*6= 10140.96
please help.
definitions: 1. definition of right triangle
2. definition of isosceles TrianglesReflexive
3. HL
4. definition of perpendicular
5. CPCTC
6. reflexive

Answers
From the two column proof below, we have seen ∠BAC ≅ ∠DAC by CPCTC
How to solve two column proof problems?The two column proof to show that ∠BAC ≅ ∠DAC is as follows:
Statement 1: ΔABD is Isosceles with base BD, AC ⊥ BD
Reason 1: Given
Statement 2: AB ≅ AD
Reason 2: Definition of isosceles Triangles
Statement 3: ∠1 and ∠2 are right angles
Reason 3: Definition of perpendicular
Statement 4: AC ≅ AC
Reason 4: Reflexive Property
Statement 5: ΔABC and ΔADC are right triangles
Reason 5: Definition of right triangle
Statement 6: ΔABC ≅ ΔADC
Reason 6: HL Congruency
Statement 7: ∠BAC ≅ ∠DAC
Reason 7: CPCTC
Read more about two column proof at; brainly.com/question/1788884
#SPJ1
Ian gets $9.00 for each hour he works. He also gets $10.00 for each day he works. He made the equation y=9x+10x where x is the number of hours he works.
Explain why his equation will not tell him how much he makes in a day.
Answers
4. Tori bought 300 shares of Mattel stock for $34.87 dollars per share. She sold all of the shares months later for $41 dollars per share. How much was her capital gain(+) or loss(-)?
Answers
The result is positive, Tori made a capital gain of $1,839 from the sale of the Mattel stock.
What is selling price ?
The selling price is the amount of money at which a product or service is sold to the customer. It is the price that the customer pays to purchase the product or service from the seller. The selling price is usually determined by considering various factors such as the cost of production, overhead expenses, marketing expenses, and the desired profit margin. The seller may also take into account the competition in the market and adjust the selling price accordingly.
According to given information :To calculate Tori's capital gain or loss, we need to find the difference between the amount she sold the shares for and the amount she bought them for.
Tori bought 300 shares of Mattel stock for $34.87 per share, so her initial investment was:
300 x $34.87 = $10,461
She later sold all of the shares for $41 per share, so she received:
300 x $41 = $12,300
To find her capital gain or loss, we subtract her initial investment from the amount she received from the sale:
$12,300 - $10,461 = $1,839
Since, the result is positive, Tori made a capital gain of $1,839 from the sale of the Mattel stock.
To know more about selling price visit :
https://brainly.com/question/29860785
#SPJ1
Please help is due tonight

Answers
The linear function that has the greatest initial value is Function C.
Function B has the greatest rate of change.
What is a function?A function is a relationship between inputs where each input is related to exactly one output.
Example:
f(x) = 2x + 1
f(1) = 2 + 1 = 3
f(2) = 2 x 2 + 1 = 4 + 1 = 5
The outputs of the functions are 3 and 5
The inputs of the function are 1 and 2.
We have,
Function A:
The initial value is o.
f(0) = 0
The rate of change.
= (f(4) - f(2)) / 4 - 2
= (10 - 5) / 2
= 5/2
= 2.5
Function B:
The initial value is
y = 3x - 1
y = 3 x 0 - 1 = 0 - 1 = -1
Let y = f(x)
The rate of change.
= (f(2) - f(1)) / (2 - 1)
= (5 - 2) / 1
= 3
Function C:
The initial value is 2.
(0, 2) is considered as when x = 0, y = 2.
Take two coordinates from the graph.
(3, 3) and (6, 4)
The rate of change.
= (4 - 3) / (6 - 3)
= 1/3
= 0.33
Thus,
Function C has the greatest initial value.
Function B has the greatest rate of change.
Learn more about functions here:
https://brainly.com/question/28533782
#SPJ1
What are the lateral area and the surface area of the cone shown below? Round the answers to
the nearest tenth. The figure is not drawn to scale.

Answers
Answer:
lateral surface area of the cone = 829.0ft²
Hence the total surface area is 1,208.9ft²
Step-by-step explanation:
lateral surface area of the cone = πrl
l is the slant side = 24ft
r is the radius = 11ft
lateral surface area of the cone = π(11)(24)
lateral surface area of the cone = 3.14 * 264
lateral surface area of the cone = 828.96ft²
lateral surface area of the cone = 829.0ft²
Total surface area = πr(r+l)
r is the radius = 11ft
l is the slant side = 24ft
Total surface area = π(11)(11+24)
Total surface area = π(11)(35)
Total surface area = 3.14 * 385
Total surface area = 1,208.9ft²
Hence the total surface area is 1,208.9ft²
Mr. Cole packed 20 pounds into a suitcase, and Mrs. Cole packed 23 pounds into the same suitcase. They then had to remove 8 pounds because it was too heavy. How many pounds was their suitcase after making it lighter?
Answers
Answer:
35 lbs is the final weight
Step-by-step explanation:
20 +23 = 43 lbs
Then they had to remove 8 lbs
43 - 8 =35
35 lbs is the final weight
Makayla is a botanist studying production of coconuts by two different groups of her coconut palms. She notices that Group 1 trees produce 25 percent more coconuts than Group 2. based on Makayla's observation, if Group 1 produced 150 coconuts, how many coconuts did group 2 produce?
Answers
If Group 1 trees produce 25 percent more coconuts than Group 2, proportionately, Group 2 trees produce 120 coconuts.
What is proportion?Proportion refers to the two ratios equated to each other.
Proportion shows how much quantity or value is contained in another.
We depict proportions using fractional values, such as fractions, decimals, and percentages.
The number of coconuts produced by Group 1 trees = 150
The percentage by which Group 1 trees produce more than Group 2 = 25%
Let Group 1's production compared to Group 2's = 1.25 (100% + 25%)
Let Group 2's production = 100% = 150/125 x 100
= 120 coconuts
Thus, Group 2 trees would produce 120 coconuts compared to Group 1 trees that produced 150, which was proportionately, 25% more.
Learn more about proportions at https://brainly.com/question/1496357
#SPJ1
Town B is 8 miles north and 17 miles west of town A. How far are
the two towns apart?
Answers
9514 1404 393
Answer:
18.8 mi
Step-by-step explanation:
The Pythagorean theorem can be used to find the straight-line distance between the towns. The distances 8 mi and 17 mi form the legs of a right triangle, whose hypotenuse is the straight-line distance.
d² = 8² +17² = 64 +289 = 353
d = √353 ≈ 18.8 . . . miles
The two towns are about 18.8 miles apart.
\( \displaystyle \rm\int_{0}^1 { ln }^{2k} \left \lgroup \frac{ ln \left \lgroup \dfrac{1 - \sqrt{1 - {x}^{2} } }{x} \right \rgroup }{ ln \left \lgroup \dfrac{1 + \sqrt{1 - {x}^{2} } }{x} \right \rgroup } \right \rgroup \: dx\)
Answers
Substitute \(x\mapsto\sqrt{1-x^2}\), which transforms the integral to
\(\displaystyle \int_0^1 \ln^{2k} \left(\frac{\ln\left(\frac{1-\sqrt{1-x^2}}x\right)}{\ln\left(\frac{1-\sqrt{1-x^2}}x\right)}\right) \, dx = \int_0^1 \ln^{2k}\left(\frac{\ln\left(\frac{1-x}{\sqrt{1-x^2}}\right)}{\ln\left(\frac{1+x}{\sqrt{1-x^2}}\right)}\right) \frac{x}{\sqrt{1-x^2}} \, dx\)
and factoring \(\sqrt{1-x^2}=\sqrt{(1-x)(1+x)}\) reduces this to
\(\displaystyle = \int_0^1 \ln^{2k}\left(\frac{\ln\left(\sqrt{\frac{1-x}{1+x}}\right)}{\ln\left(\sqrt{\frac{1+x}{1-x}}\right)}\right) \frac x{\sqrt{1-x^2}} \, dx\)
The inner logarithms differ only by a sign, so that
\(\displaystyle = \int_0^1 \ln^{2k}(-1) \frac x{\sqrt{1-x^2}} \, dx\)
Using the principal branch of the complex logarithm, we have
\(\ln(-1) = \ln|-1| + i\arg(-1) = i\pi\)
and hence
\(\displaystyle \int_0^1 \ln^{2k} \left(\frac{\ln\left(\frac{1-\sqrt{1-x^2}}x\right)}{\ln\left(\frac{1-\sqrt{1-x^2}}x\right)}\right) \, dx = (i\pi)^{2k} \underbrace{\int_0^1 \frac x{\sqrt{1-x^2}} \, dx}_{=1} = \boxed{(-\pi^2)^k}\)
where I assume k is an integer.
What number is
1/3 of 12?
Answers
Answer: 4.
Step-by-step explanation:
1/3 of 12?
12 divided by 3 = 4.
The perimeter of a rectangle is 108 cm. If the length is 30 cm, how wide is the rectangle?
A) First write an equation you can use to answer this question. Use w as your variable in the equation.
The equation is
B) Solve your equation in part [A] to find the width of the rectangle.
Answer: The rectangle is
cm wide.
Answers
Answer:
Step-by-step explanation:
A) The equation for the perimeter of a rectangle is given by 2 * (length + width), so we can write the equation for this rectangle as:
2 * (30 + w) = 108
B) To find the width of the rectangle, we can solve for w:
60 + 2w = 108
2w = 48
w = 24
So, the width of the rectangle is 24 cm.
Type a digit that makes this statement true.14,276,41 is divisible by 6.
Answers
Given the expression, let x represent the missing number.
\(14,276,41x\)for it to be divisible by 6, it must be even and divisible by 3.
For it to be even, the possible values of x is 0,2,4,6,8.
also for it to be divisible by 3, the sum of all the digits must be
PLS HELP ASAP GUYS! 50 POINTS!! Match the verbal expression to its correct algebraic expression.
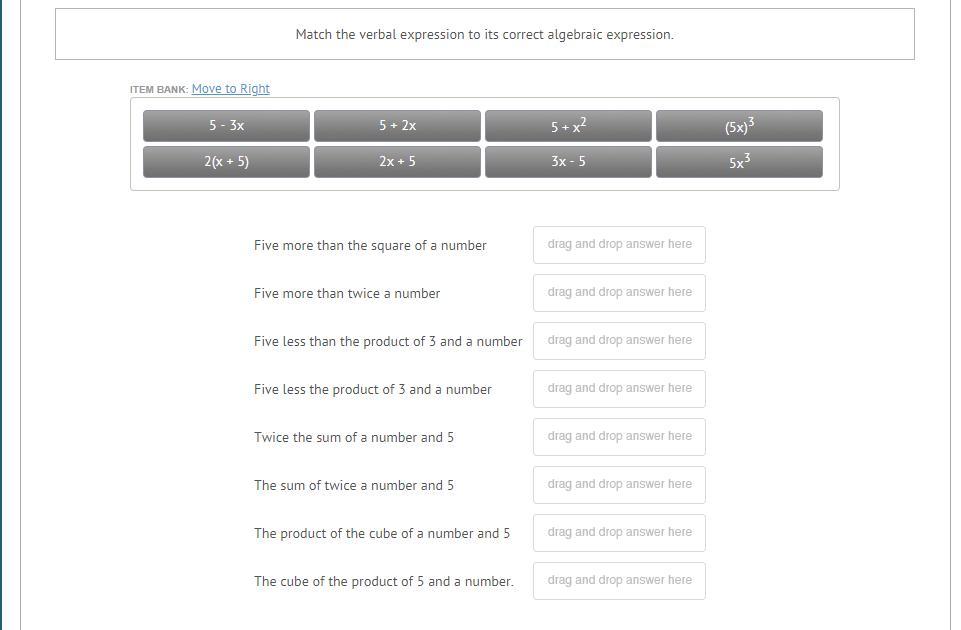
Answers
The second one is 5+2x
The third one is 3x-5
The fourth one is 5-3x
The fifth one is 2(x+5)
The sixth one is 2x+5
The seventh one is 5x^3
The eight one is (5x)^3
I think this is all of them :)
what is the formula to find time from distance
Answers
The formula to find time from distance is time = distance/speed
How to determine the formula of time?As a general rule, the formula of speed is
Speed = Distance/Time
Multiply both sides by Time
Time * Speed = Distance
Divide both sides by Speed
he formula to find time from distance
Hence, the formula to find time from distance is time = distance/speed
Read more about distance at:
https://brainly.com/question/4931057
#SPJ1
Please answer this in two minutes

Answers
Answer:
1/2
Step-by-step explanation:
Rise over run solution:
choose a point and go 1 unit up and 2 to the right!
hope this helped
Hey there! :)
Answer:
m = 1/2.
Step-by-step explanation:
Find the slope using the slope formula:
\(m = \frac{\text{rise}}{\text{run}} = \frac{y_2 - y_1}{x_2 - x_1}\)
Points on the graph we can use are:
(0, 3) and (2, 4)
Plug these into the formula:
\(m = \frac{4-3}{2-0}\)
Simplify:
\(m = \frac{1}{2}\)
Therefore, the slope is 1/2.
Solve the system by substitution.
x - 5y = 1
- 2x + 9y = -1
what is the solution?
Answers
Answer:
x = − 4 .y = − 1
Step-by-step explanation:
Search
When solving a word problem using a system of equations, how many equations
must you create when there are two unknowns?
a) 1
b) 2
c) 3
d) 4
Answers
Answer:
The answer for the above question is:
b)2
When solving a word problem using a system of equations with two unknowns, you must create two equations. So, correct option is B.
The reason is that each unknown in the problem requires an equation to represent its relationship with the other variables.
For example, let's say you have two unknowns, x and y. You need two equations to define the relationships between these variables. These equations can be represented as:
Equation 1: x + y = 10 (This equation represents the relationship between x and y based on the given information in the problem.)
Equation 2: 2x - y = 4 (This equation represents another relationship between x and y based on additional information provided in the problem.)
With a system of two equations involving two unknowns, you can use algebraic methods such as substitution or elimination to solve for the values of x and y.
Having only one equation would not be enough to determine unique values for both x and y, as there would be an infinite number of possible solutions. On the other hand, having more than two equations might lead to over-determining the system, making it inconsistent or redundant.
Therefore, two equations are the minimum required to solve for two unknowns effectively. So, correct option is B.
To learn more about equations click on,
https://brainly.com/question/10255500
#SPJ2
hey there Ms or Mr i don't understand the problem here could yiu please help me out?

Answers
When two angles are on oposite sides of a line that divide two parallel lines, they are called alternate exterior angles. When this happens the values of these two angles is the same.
In this case angles "1" and "3" are alternate exterior angles, therefore they are congruent.
\(\begin{gathered} \measuredangle3=\measuredangle1 \\ \measuredangle3=2x+20 \end{gathered}\)We need to calculate the value of "x" to know its measurement. The angles "1" and "2" are suplementary, which means that their sum is equal to 180, we can use this to find "x".
\(\begin{gathered} \measuredangle1+\measuredangle2=180 \\ 2x+20+4x+10=180 \\ 6x+30=180 \\ 6x=180-30 \\ 6x=150 \\ x=\frac{150}{6}=25 \end{gathered}\)We can find the value of the angle 3 by using 25 as the value of x.
\(\begin{gathered} \measuredangle3=2\cdot25+20 \\ \measuredangle3=50+20 \\ \measuredangle3=70 \end{gathered}\)The value of the angle 3 is 70 degrees.
I need help with my homework


Answers
To find the length of a line segment in a circle, use the formula \(d = 2r\) \(sin(t/2)\) , where r is the radius of the circle and t is the angle between the radii. The length of segment DE is \(5\) units.
What is the formula for circle segment length?We can use the similar triangles property to find the missing length of segment DE in the given figure. Because triangles ABD and CBE are similar, we can use a proportion to find the length of DE:
\(CB/BE = AB/BD\)
With the given values, we get:
\(3/6 = 5/(5 + DE)\)
When we simplify and solve for DE, we get:
\(3(5 + DE) = 6 * 5 \s15 + 3DE = 30\)
\(3DE = 15 \sDE = 5\)
Therefore, segment DE has a length of 5 units.
Learn more about circle here:
https://brainly.com/question/28612561
#SPJ1
Hi can any one teach me this constant difference

Answers
The constant differences between the consecutive terms are 2 (a); 2 (b), -3 (c), 7 (d), 1(e), and 6(f).
How do you find the constant difference in a sequence of numbers?In math, the constant difference can be defined as the number that defines the pattern of a sequence of numbers. This means that number that should be added or subtracted to continue with the sequence.
Due to this, to determine the constant difference it is important to observe the pattern and find out the number that should be added. For example, if the sequence is 2, 4, 6, 8, there is a difference of 2 between each of the numbers and this is the constant difference.
Learn more about numbers in https://brainly.com/question/24908711
#SPJ1
72/60
Write
in simplest form.
Answers
Answer:
\(1 \frac{1}{6}\) or 6/5
Step-by-step explanation:
72/60
= 6/5
= 1 1/5
= 1.2 (in decimal)
Answer:
6/5
Step-by-step explanation:
The graph of the function, B(x), is shown below. Determine the following values for the function:B(x) = 0B(x) = -1B(x) = 2Complete your work in the space provided.
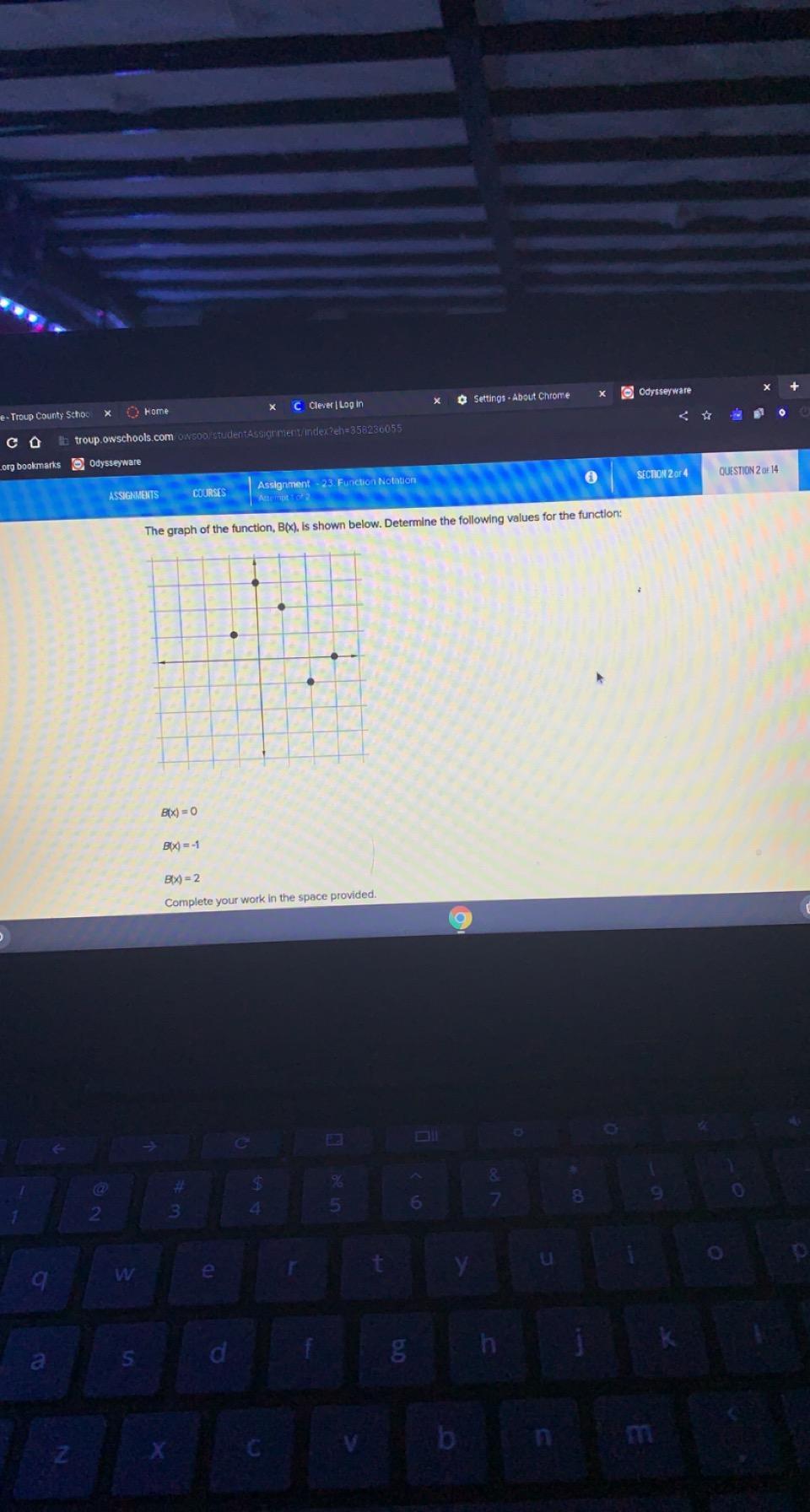
Answers
Given the following output values;
B(x) = 0
B(x) = -1
B(x) = 2
According to the question, we need to determine the corresponding x-values on the xy-plane for the given outputs (y values)
To get the required values for the function, we need to locate each of the B(x) values on the y-axis of the graph, the corresponding x-value(s) are the required values for the function.
For the function B(x) = 0.
From the graph, you can see that the corresponding x-coordinate at the point where B(x) = 0 is 3. Hence the value for the function B(x) = 0 is 3
For the function B(x) = -1.
From the graph, you can see that the corresponding x-coordinate at the point where B(x) = -1 is 2. Hence the value for the function B(x) = -1 is 2
For the function B(x) = 2.
From the graph, you can see that the corresponding x-coordinate at the point where B(x) = 2 is 1. Hence the value for the function B(x) = 2 is 1