There are 5 fourth-grade classes at Lincoln School. The table below shows the number of students in each class. Which is the median number of students per class?
23
24
25
26
Answers
24 students per class
Related Questions
The constraints of a problem are listed below. What are the vertices of the feasible region? 2x+3y≥12 5x+2y≥15 x ≥ 0 y ≥ 0
Answers
The vertices of the feasible region are (0 , 15/2) , (21/11 , 19/11) and (6 , 0)
Given, the constraints of a problem
2x+3y≥12
5x+2y≥15
x ≥ 0
y ≥ 0
On solving the equations, we get
( 2x + 3y ≥ 12 ) × 2
( 5x + 2y ≥ 15 ) × 3
4x + 6y ≥ 24
15x + 6y ≥ 45
On subtracting, we get
11x ≥ 21
x ≥ 21/11
x = 21/11
On putting the value of x, we get
42/11 + 3y = 12
y = 19/11
Hence, the vertices of the feasible region are (0 , 15/2) , (21/11 , 19/11) and (6 , 0)
Learn more about Linear Programming Problems here https://brainly.com/question/25828237
#SPJ9
translate in terms of x then solve the algebra equation the sum of a number and 3 is subtracted from 10 the result is 5
Answers
Answer:
x=2
Step-by-step explanation:
10 - (x + 3) = 5
To solve for x, we can start by simplifying the left side of the equation:
10 - (x + 3) = 5
10 - x - 3 = 5
7 - x = 5
Next, we can isolate x on one side of the equation by subtracting 7 from both sides:
7 - x = 5
7 - x - 7 = 5 - 7
-x = -2
Finally, we can solve for x by dividing both sides of the equation by -1:
-x = -2
x = 2
Therefore, the solution to the equation is x = 2.
f(x) = x +3, g(x) = x - 3. Find(f-g)(x)
Answers
Steph, let's recall that composite function is a function that depends on another function. A composite function is created when one function is substituted into another function.
Given f(x) = x +3, g(x) = x - 3
• f (g(x)) = f (x - 3)
,• (x - 3) + 3
,• x - 3 + 3
,• x
• g (f(x)) = g (x + 3)
,• (x + 3) - 3
,• x + 3 - 3
,• x
For the given functions, f (g(x)) = g (f(x))
Student became unresponsive, no final interaction
A coin is tossed 6 times, find the probability of getting 3 heads.
Answers
Answer:
3/6
Step-by-step explanation:
Answer:
0.31 if you get exactly 3 heads or 0.66 probability if you get at least 3 heads, or 50%
Step-by-step explanation:
0.31 is the probability of getting exactly 3 Heads in 6 tossed
0.66 is the probability of getting at least 3 heads
Which is larger, 7 feet or 84 inches?
Answers
Answer:
They are equal
Step-by-step explanation:
12 inches is equal to 1 foot. 7 feet is equal to 12x7 which is equal to 84. Therefore, they are the same.
If this answer has helped you, please mark this as brainliest
Both numbers 7 feet or 84 inches are equal.
What is Measurement unit?A measurement unit is a standard quality used to express a physical quantity. Also it refers to the comparison between the unknown quantity with the known quantity.
Given that;
Two numbers are,
⇒ 7 feet and 84 inches
We know that;
⇒ 1 feet = 12 inches
Hence, We get;
7 feet = 12 × 7 inches
= 84 inches
Therefore, Both numbers 7 feet or 84 inches are equal.
Learn more about the measurement unit visit:
https://brainly.com/question/777464
#SPJ3
What are the mathematical names for these shapes

Answers
Answer:
Step-by-step explanation:
The top is rectangular pyramid
The second a sphere
The third is a cube
Triangular pyramid is the last
Which answer choice correctly simplifies the expression Hint: Use distributive property and watch your signs. -4 (x2 - 2xy + 5y2 - 3)? O-4x2 - 2xy + 5y2 - 3 4x2 - xy + 20y2 - 12 0-4x2 + xy - 20y2 +12
Answers
Answer: -4x^2 + 8xy - 20y^2 + 12
Step-by-step explanation:
-4 (x2 - 2xy + 5y2 - 3)
-4(x^2) = -4x^2
-4(-2xy) = 8xy
-4(5y^2) = -20y^2
-4(-3) = 12
The ratio of 36 apples to 18 children
Answers
It could be 1:1 or 2:1 if you dont give them more than 1 apple and save some
Step-by-step explanation:
write the equation of a tangent line to the circle with center 93,6) and the line contains point (-2,3)
Answers
The equation of a tangent line to the circle is, \(x^{2} +y^{2}\) = 34
Given that,
The equation of a tangent line to the circle with center = (3,6)
The line contains point = (-2,3)
For a circle or curve, the tangent is a line or line segment that touches the circle at one point only. For a circle, the tangent will be perpendicular to a radius drawn to the tangent point.
A tangent to a circle at point P with coordinates is a straight line that touches the circle at P. The tangent is perpendicular to the radius which joins the centre of the circle to the point P. As the tangent is a straight line, the equation of the tangent will be of the form y = m x + c
The equation of circle of radius r and center (h , k) is given by
\((x-h)^{2}\) + \((y-k)^{2}\) = \(r^{2}\) (Equation-1)
And it is given that the center is (3,6) and it passes through (-2,3).
So values of h and k are (3,6) each and values of x and y are 2 and respectively .
Substituting these values in the equation, we will get
(h , k) = (3,6)
We can substitute h , k values in equation-1,
\((x-h)^{2}\) + \((y-k)^{2}\) = \(r^{2}\)
\((x-3)^{2}\) + \((y-6)^{2}\) = \(r^{2}\)
Then we can substitute x , y values,
So,
We can write,
( x , y ) = (-2 , 3)
\((-2-3)^{2}\) + \((3-6)^{2}\) = \(r^{2}\)
\((-5)^{2}\) + \((-3)^{2}\) = \(r^{2}\)
25 + 9 = \(r^{2}\)
34 = \(r^{2}\)
Substituting the values of h, k and r, we will get
\(x^{2} +y^{2}\) = 34
Therefore,
The equation of a tangent line to the circle is, \(x^{2} +y^{2}\) = 34
To learn more about Tangent circle visit :
brainly.com/question/23265136
#SPJ4
Find the equation of the line through the points (−2,−10)
and (−2,−5).
Answers
Answer:
x = -2
Step-by-step explanation:
The line passing through the points (-2, -10) and (-2, -5) is a vertical line because both points have the same x-coordinate (-2).
Therefore, the equation of the line is simple:
x = -2
This means that for any value of y, the corresponding value of x is always -2. Visually, this line looks like a straight vertical line passing through the point (-2, -10) and (-2, -5) on the coordinate plane.
Answer:
Step-by-step explanation:
the point (-3, 2) is translated 2 units to the left and 7 units up. what are the new coordinates
Answers
Answer:
(-5, 9)
Step-by-step explanation:
(-3-2, 2+7)= (-5,9)
Hey can I get some help real quick
Answers
Answer: sure, with what though?
Step-by-step explanation:
let y1 and y2 are independent random variables that are both uniformly distributed on the interval (0,1). find p(y1 <1
Answers
the probability of y1 being less than 1 is 1, regardless of the actual value of y1. P(y1 < 1) = 1
Since y1 and y2 are both uniformly distributed on the interval (0,1), this means that all possible values of y1 and y2 are equally likely. Therefore, the probability of y1 being less than 1 is 1, since any value of y1 between 0 and 1 has the same probability of occurring. This means that the probability of y1 being less than 1 is 1.
Since y1 and y2 are both uniformly distributed on the interval (0,1), this means that all possible values of y1 and y2 between 0 and 1 are equally likely to occur. This means that the probability of y1 being less than 1 is the same as the probability of y1 being equal to any value between 0 and 1. Since this probability is the same for all possible values of y1, the probability of y1 being less than 1 is 1, regardless of the actual value of y1. This is because any value of y1 between 0 and 1 has the same probability of occurring, meaning that the probability of y1 being less than 1 is 1.
Learn more about probability here
https://brainly.com/question/11234923
#SPJ4
PLEASE HELP!! What is the surface area of the cone?
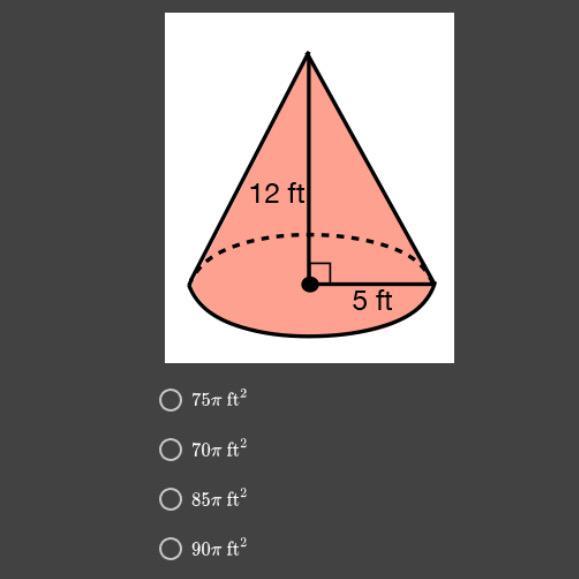
Answers
Hope this helped
The sum of the 112th term of the geometric series is 256 and the common ratio is 3/4. Find the first term of the first geometric series.

Answers
Answer:
First term = 64
Step-by-step explanation:
We are given the formula for the nth term of a geometric series to be;
S_n = (a1(1 - rⁿ))/(1 - r)
Where:
S_n is the sum of n terms
A1 is first term
r is common ratio
We are given;
S_112 = 256
r = ¾
Thus;
256 = a1(1 - ¾^(112))/(1 - ¾)
256 = a1(4)
a1 = 256/4
a1 = 64
if JB and CI are medians and JW=6x+2 and JB=10x+1, calculate the lenght of the segment JW

Answers
JB is a median
CI is a median
JW=6x+2
JB=10x+1
If W is the centeroidof the triangle, determined by medians JB, CI and KA, it means that it cuts both line segments following the ratio 2:1 → meaning that the segment JW is 2/3 of the segment JB while the segment WB is 1/3 of JB.
This means that the ratio between segments JW and JB is as follows:
\(\frac{2}{3}=\frac{JW}{JB}\)Replece it with the given expressions:
\(\frac{2}{3}=\frac{6x+2}{10x+1}\)Use cross multiplication between both fractions:
\(\begin{gathered} 2\cdot(10x+1)=3(6x+2) \\ 20x+2=18x+6 \end{gathered}\)And finally solve for x
\(\begin{gathered} 20x-18x=6-2 \\ 2x=4 \\ x=2 \end{gathered}\)The unknown value is x=2
Now you can calculate the length of segment JW as:
\(\begin{gathered} JW=6x+2 \\ JW=6\cdot2+2 \\ JW=14 \end{gathered}\)The length of segment JW is 14 units.

pls help i give brainliest

Answers
The required number of nickels and dimes is given as 12 and 9 respectively.
The process in mathematics to operate and interpret the function to make the function or expression simple or more understandable is called simplifying and the process is called simplification.
here,
Given a system of the equation,
n + d = 21
n = 21 - d - - - - - (1)
0.05n + 0.10d = 1.50 -----(2)
Substitute n in the above equation,
0.05[21 - d] + 0.10d = 1.50
1.05 - 0.05d + 0.10 d = 1.50
0.05d = 0.45
d = 0.45/0.05
d = 9
Now, put d in equation 1,
n = 21 - 9
n = 12
Thus, the required number of nickels and dimes is given as 12 and 9 respectively.
Learn more about simplification here:
https://brainly.com/question/12501526
#SPJ1
Of the last 100 customers entering a computer shop, 25 have purchased a computer. If the relative frequency method for computing probability is used, the probability that the next customer will purchase a computer is
Answers
Answer: 0.25
Step-by-step explanation:
The relative frequency of the customers that buy computers is equal to the number of customers that bought a computer divided the total number of customers that entered the shop.
p = 25/100 = 0.25
If we take this as the probability, then the probability that the next customer that enters the shop buys a computer is 0.25 or 25%
The rate, r, at which you drive a car is related to the distance, d, and time, t, in the
equation
d
r =
If you increase the distance and keep your rate constant (stays the same), what
happens to your time?
A.Your time will decrease
B.Not enough information to tell
C.Your time will increase
D.Your time will stay the same
Answers
Answer:
C. Your time will increase
Step-by-step explanation:
Since r= d/t, then if you increase d, t will decrease since r is staying the same
A positive real number is 1 less than another. When 2 times the larger is added to the square of the smaller, the result is 13. Find the numbers. (If applicable, write your answers in the form p±q√r)
Answers
From the problem, we know that:
2(x + 1) + x^2 = 13
Simplifying and rearranging:
x^2 + 2x - 11 = 0
Using the quadratic formula:
x = (-2 ± sqrt(2^2 - 4(1)(-11))) / (2(1))
x = (-2 ± sqrt(48)) / 2
x = (-2 ± 4sqrt(3)) / 2
x = -1 ± 2sqrt(3)
Since the problem states that the numbers are positive, we can ignore the negative solution. Therefore, the smaller number is:
x = -1 + 2sqrt(3)
And the larger number is:
x + 1 = 2sqrt(3)
So the two numbers are -1 + 2sqrt(3) and 2sqrt(3).
The larger triangle is dilated to form the smaller triangle what is the scale factor?

Answers
Answer:
The answer is 1/2
Step-by-step explanation:
3 and 6 are the known sides of the triangle as you can see three is half of six making it a 1/2 dilation
\(\dfrac{6}{3} = 2\)
the scale factor is
1 : 2
A. Give two examples of addition of Like Fractions.
B. Give two examples of Subtraction of Like Fractions
C. Give three examples of multiplication of Fractions.
D. Give two examples of Addition of Unlike Fractions.
E. Give two examples of Division of Fractions.
IM GIVING BRAINLIEST AND 30 POINTS!!
Answers
Answer:
A: 3/5 + 2/5 = 5/5
A: 3/5 + 1/5 = 4/5
B: 3/5 - 2/5 = 1/5
B: 3/5 - 1/5 = 2/5
C: 3/5 x 2/5 = 6/25
C: 3/5 x 1/5 = 3/25
C: 2/5 x 1/5 = 2/25
D: 1/2 + 1/4 = 3/4
D: 4/5 + 4/10 = 6/5
E: 4/6 ÷ 2/6 = 2
E: 1/6 ÷ 1/6 = 1
Step-by-step explanation:
Here's a plot showing the interest rate on a 3-month bond from 1950 to 1980, and a regression model fit to the relationship between the Rate (in %) and Years since 1950. Complete parts a through d. a) What is the correlation between rate and year? b) Interpret the slope and intercept. On average, interest rates during this period at about % per year, starting from an interest rate of about c) What does this model predict for the interest rate in the year 2000? %
Answers
a) Positive correlation. b) Slope = 0.02, Intercept = 3.17; rate increases ~2%/yr, starting at 3.17%. c) Predicts interest rate of 5.17% in 2000.
a) The correlation between rate and year can be determined by constructing a scatter plot. From the given plot, we can see that there is a positive correlation between the two variables, meaning that as the year increases, the rate increases as well.
b) The regression model fit to the data provides the slope and intercept of the line of best fit. The slope is 0.02, which means that the rate is increasing by 0.02% per year. The intercept is 3.17, which means that the interest rate starts at 3.17% in 1950.
c) The model predicts that the interest rate in the year 2000 will be 5.17%. This can be calculated by plugging in 2000 for the year in the model equation (Rate = 0.02*Year + 3.17).
d) In summary, the regression model fit to the data shows that on average, interest rates during this period increased by about 0.02% per year, starting from an interest rate of about 3.17% in 1950. The model predicts that the interest rate in the year 2000 will be 5.17%.
Learn more about slope here
https://brainly.com/question/3605446
#SPJ4
The U.S. Bureau of Labor Statistics is a government agency that collects information about jobs in the U.S. In 2014, the Bureau reported that police officers had a median yearly salary of $52,936.
Calculate the average hourly wage for police officers. Round to the nearest cent. Assume that police officers generally work 40 hours a week. There are 52 weeks in the year.
Answer = $ per hour
Answers
Answer:25.45
Step-by-step explanation:
52936/1 year x 1 year/52 weeks x 1 week/40hours
And ice cream stand sold $1600 worth of ice cream on Saturday which was four times the amount sold on Friday how much money did the ice cream man collect on Friday no
Answers
Answer:
$400
Step-by-step explanation:
Saturday: $1600, 4 times the amount of Friday
Friday: 1/4 the amount of Saturday
Friday: 1/4 * $1600 = $400
a rectangular auditorium seats 2244 people. The number of seats in each row exceeds the number of rows by 7. Find the number of seats in each row
Answers
Number of seats in each row is 51 given that a rectangular auditorium seats 2244 people and number of seats in each row exceeds the number of rows by 7. This can be obtained by assuming the value of number of seats in each row, forming quadratic equation and using quadratic formula to find root.
Find the number of seats in each row:
Here in the question it is given that,
a rectangular auditorium seats 2244 peoplenumber of seats in each row exceeds the number of rows by 7We have to find the number of seats in each row.
Let us assume that the number of seats in each row be x.
From the given statement, number of seats in each row exceeds the number of rows by 7, we can write that,
Number of seats in one row = Number of rows + 7
x = Number of rows + 7
⇒ Number of rows = x - 7
Total number of seats in the auditorium can be written as,
⇒ (Number of seats in one row)(Number of rows) = Total number of seats
(x)(x - 7) = 2244
x² - 7x = 2244
⇒ x² - 7x - 2244 = 0
By using quadratic formula we can find the root,
x = (-b ± √b² - 4ac)/2a
here in the question, a = 1, b = -7, c = -2244
√b² - 4ac = √(-7)² - 4(1)(-2244)
√b² - 4ac = √49 + 8976
√b² - 4ac = √9025
√b² - 4ac = 95
x = (-b ± √b² - 4ac)/2a
x = (7 ± 95)/2
x = 102/2 or x = -88/2
⇒ x = 51 or x = -44
Hence number of seats in each row is 51 given that a rectangular auditorium seats 2244 people and number of seats in each row exceeds the number of rows by 7.
Learn more about quadratic formula here:
brainly.com/question/26926523
#SPJ9
To raise money the youth club bought 90 kg of pecans for $297.90. They sold the pecans in 250 g bags for $1.90 each. How much profit did they make?
Answers
Answer:
Profit = $6,922.1
Step-by-step explanation:
Total weight of pecans = 950 kg
1 kg = 1000g
Total weight of pecans in gram = 950 *1000 g = 950,000 g
Note : we have calculated weight in gram as later in question weight of pecans in bag is given in gram so to make uniformity in unit of weight)
Given quantity one bag can store = 250 g
let there be x bag to store 950,000 g of pecan
weight of x bag = quantity one bag can store*x = 250x (this will be equal to total weight of pecan as given)
250 x= 950,000 g
=> x = 950000/250 = 950*4 = 3800
Thus, there are 3800 bags.
Selling price for 1 bag = $1.90
Selling price for 3800 bag = $1.90*3800 = $7,220
we know profit = selling price - cost price
given cost price of 950 kg pecan = $297.90
Profit = $7,220 - $297.90 = $6,922.1 (answer)
Does (8, 7) make the equation y = x - -3 true?
Answers
Answer:
No.
Step-by-step explanation:
7=8-(-3)
7=8+3
7≠11
find 9 rational no. between 8/7 and 17/10.
Answers
Answer:
\(\dfrac{81}{70},\dfrac{82}{70},\dfrac{83}{70},\dfrac{84}{70},\dfrac{85}{70},\dfrac{86}{70},\dfrac{87}{70},\dfrac{88}{70},\dfrac{89}{70}\)
Step-by-step explanation:
We need to find 9 rational number between \(\dfrac{8}{7}\ \text{and}\ \dfrac{17}{10}\)
We make the denominators of both fractions same. So,
\(\dfrac{8}{7}\times \dfrac{10}{10}=\dfrac{80}{70}\)
and
\(\dfrac{17}{10}\times \dfrac{7}{7}=\dfrac{119}{70}\)
The rational number are:
\(\dfrac{81}{70},\dfrac{82}{70},\dfrac{83}{70},\dfrac{84}{70},\dfrac{85}{70},\dfrac{86}{70},\dfrac{87}{70},\dfrac{88}{70},\dfrac{89}{70}\)
Please Help
Solve x= 10+5/2
Answers
Answer:
Step-by-step explanation:
20/2 + 5/2 = 25/2 = 12 1/2