There are 55 trucks and c cars in a parking lot. The equation 55 + c = 78 can be used to find c. What is the value of c?
Answers
Answer:
c= 23
Step-by-step explanation:
55+c = 78
-55. -55
----------------
c = 23
Related Questions
please help write the reasons that are needed to complete the proof in the picture

Answers
Answer:
a. Given
b. thru any 2 points there exists a line (you can draw a line)
c. Definition of Regular Polygon
d. Definition of Regular Polygon
e. Given
f. Def of Midpoint
g. SAS: Side-Angle-Side congruence
h. CPCTC - Corresponding Parts of Congruent Triangles are Congruent
i. Definition of Regular Polygon
j. Reflexive
k. SSS: Side-Side-Side congruence
l. CPCTC
Step-by-step explanation:
I encourage you to look up all of the above reasons to get a better understanding of what they are!!
What is the solution to the equation 6 m = 60? m = 10 m = 50 m = 66 m = 360
Answers
Answer:
Just simplify by isolating the variable.
To do this, you need to get rid of the coefficient.
This means dividing both sides by 6.
6m / 6 = m
60 / 6 = 10
m = 10 is the answer.
Step-by-step explanation:
What’s 9 X 3/9 answer…………………………………….
Answers
Answer:
9 x 3/9
= 39 ⋅ 3= 2727/9
27 ÷ 9
= 3Step-by-step explanation:
You're welcome.
4-x/3= y solve for x
Answers
Answer:
x=-3y+12
Step-by-step explanation:
\(4-\frac{x}{3}=y\)
You can subtract y from both sides and add (x/3) to both sides to isolate the variable that you're trying to solve.
\(-y+4=\frac{x}{3}\)
Multiply both sides by 3
\(-3y+12=x\)
Which coordinates best represents the vertex of the graph first correct answer gets Brianliest

Answers
Answer:
The vertex of the graph is:
the minimum point for a parabola that opens upwardsthe maximum point for a parabola that opens downwardsAs this parabola opens upwards, the vertex is the minimum point.
From inspection of the graph, vertex = (-3, -1)
Equation of the graph
From inspection we can see that the x-intercepts are when
x = -4 and x = -2
\(\sf x = -4 \implies x+4=0\)
\(\sf x = -2 \implies x+2=0\)
Therefore:
\(\sf y=(x+4)(x+2)\)
Expand:
\(\sf \implies y=x^2+6x+8\)
Answer:
\(B)f(x) = {x}^{2} + 6x + 8\)
Step-by-step explanation:
Let \( f(x)=x^2\) be the parent function. With transformation of function, firstly,we know that,
We can move it up or down by adding a constant to the y-valuealgebraically
g(x)=x²+CClearly, The parabola is moved down by 1 unit thus, C is -1. Therefore our function transforms to
f(x)=x²-1secondly, we know that,
We can move it left or right by adding a constant to the x-valuealgebraically,
g(x)=(x+C)²in case,
C is positive, g(x) moves to the left and vise versaSince the parabola is moved left by 3 unit, C is +3, and hence Our function eventually becomes
\(f(x) = (x + 3 {)}^{2} - 1\)simplifying it yields:
\(\implies \boxed{f(x) = {x}^{2} + 6x + 8}\)
Hence,B is our required answer
Determine the turning points and distinguish between them when necessary y=x³ - 3x - 9x + 4
Answers
The turning points of the function y = x³ - 3x² - 9x + 4 are (3, -23) and (-1, 9).
To determine the turning points of the given function y = x³ - 3x² - 9x + 4, we need to find the critical points where the derivative of the function is equal to zero.
1. Find the derivative of the function:
y' = 3x² - 6x - 9
2. Set the derivative equal to zero and solve for x:
3x² - 6x - 9 = 0
3. Factorize the quadratic equation:
3(x² - 2x - 3) = 0
4. Solve the quadratic equation by factoring or using the quadratic formula:
(x - 3)(x + 1) = 0
This gives us two possible values for x: x = 3 and x = -1.
5. Substitute these critical points back into the original function to find the corresponding y-values:
For x = 3:
y = (3)³ - 3(3)² - 9(3) + 4
= 27 - 27 - 27 + 4
= -23
For x = -1:
y = (-1)³ - 3(-1)² - 9(-1) + 4
= -1 - 3 + 9 + 4
= 9
6. Therefore, the turning points are (3, -23) and (-1, 9).
Note: It appears that there was a typo in the original equation, where the term "-9x" should have been "-3x²". The above solution assumes the corrected equation.
For more such questions on points, click on:
https://brainly.com/question/26865
#SPJ8
In ANOP, the measure of P=90°, PN = 95 feet, and OP = 31 feet. Find the measure
of ZO to the nearest degree.
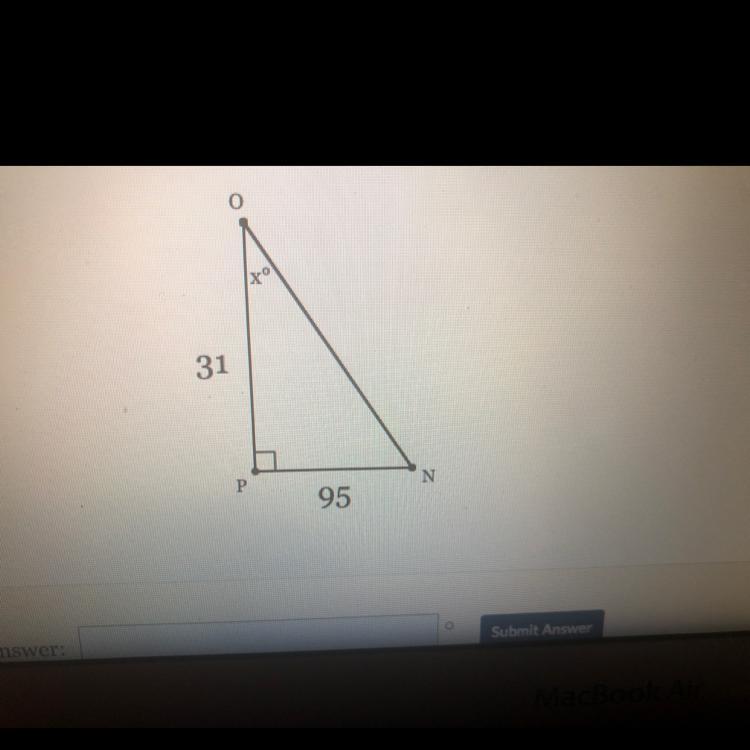
Answers
Answer: 72
Step-by-step explanation:
The length of time a person takes to decide which shoes to purchase is normally distributed with a mean of 8.21 minutes and a standard deviation of 1.90. Find the probability that a randomly selected individual will take less than 5 minutes to select a shoe purchase. Is this outcome unusual?Probability is 0.045, which is usual as it is not less than 5%Probability is 0.954, which is unusual as it is greater than 5%Probability is 0.954, which is usual as it is greater than 5%Probability is 0.045, which is unusual as it is less than 5%
Answers
Given:
\(\begin{gathered} mean(\mu)=8.21 \\ standard-deviation(\sigma)=1.90 \end{gathered}\)To Determine: The probability that a randomly selected individual will take less than 5 minutes to select a shoe purchase
Solution
P(x<5)
The z score formula is given as
\(z=\frac{x-\mu}{\sigma}\)Substitute the given into the formula
\(z=\frac{5-8.21}{1.90}\)\(\begin{gathered} z=-\frac{3.21}{1.9} \\ z=-1.68947 \end{gathered}\)The probabilty would be
\(\begin{gathered} P(x<-1.68947)=0.04556 \\ \approx0.045 \\ \approx4.5\% \end{gathered}\)Hence, the probability is 0.045, which is unusual as it is less than 5%
Which data set could be represented by the box plot shown below? A horizontal boxplot is plotted along a horizontal axis marked from 10 to 26, in increments of 1. A left whisker extends from 12 to 15. The box extends from 15 to 21 and is divided into 2 parts by a vertical line segment at 19. The right whisker extends from 21 to 24. All values estimated. Choose 1 answer: Choose 1 answer: (Choice A) 13 1313, 15 1515, 15 1515, 17 1717, 19 1919, 19 1919, 20 2020, 22 2222, 24 2424 A 13 1313, 15 1515, 15 1515, 17 1717, 19 1919, 19 1919, 20 2020, 22 2222, 24 2424 (Choice B) 12 1212, 15 1515, 15 1515, 17 1717, 19 1919, 19 1919, 20 2020, 22 2222, 24 2424 B 12 1212, 15 1515, 15 1515, 17 1717, 19 1919, 19 1919, 20 2020, 22 2222, 24 2424 (Choice C) 12 1212, 15 1515, 15 1515, 17 1717, 20 2020, 20 2020, 20 2020, 22 2222, 24 2424 C 12 1212, 15 1515, 15 1515, 17 1717, 20 2020, 20 2020, 20 2020, 22 2222, 24 2424 (Choice D) 12 1212, 15 1515, 17 1717, 17 1717, 19 1919, 19 1919, 22 2222, 22 2222, 24 2424 D 12 1212, 15 1515, 17 1717, 17 1717, 19 1919, 19 1919, 22 2222, 22 2222, 24 2424

Answers
The dataset represented by the given box plot is 12, 15, 15, 17, 19, 19, 20, 22, 24 option B.
What is box plot?A box plot, sometimes called a box whisker plot, shows the distribution of a dataset graphically. The minimum value, the first quartile (25th percentile), the median (50th percentile), the third quartile (75th percentile), and the maximum value are the five main values used to standardise this method of displaying the distribution of data.
Two whiskers that extend from a rectangular box make up a box plot. The range of values between the first and third quartiles is represented by the box, which is known as the interquartile range (IQR).
From the given box plot we observe that the minimum value is 12 and the maximum value is 24.
Here, the median is 19.
From the information the two data set that have the corresponding values are:
12, 15, 15, 17, 19, 19, 20, 22, 24
12, 15, 17, 17, 19, 19, 22, 22, 24
The lower quartile is 15.
The upper quartile is 21.
Calculating the lower quartile for the data sets:
12, 15, 15, 17, 19, 19, 20, 22, 24
Lower quartile = 15
Hence, the dataset represented by the given box plot is 12, 15, 15, 17, 19, 19, 20, 22, 24 option B.
Learn more about box plot here:
https://brainly.com/question/1523909
#SPJ1
Question
The table below gives the value of a hypothetical $10,000 investment in a certain money market fund. Use a calculator or a
spreadsheet program to find an exponential regression model of the formy - ab' for the data set, and use it to estimate
the value of the investment 12 years after purchase.
Time (years) Value of Investment (USD)
0
10,000
1
11,000
2
12, 100
3
13,310
4
14,641
5
16,105,1
6
17,715.61
Answers
Answer:
$31,384.28
Step-by-step explanation:
If you're familiar with Pascal's triangle, you probably recognize the digits of the given values match successive lines of that triangle. This immediately suggests that the base of the exponential function is exactly 1.1, and the model can be written immediately as ...
y = 10000(1.1^x)
For x=12, the value of the investment is predicted to be ...
y = 10,000(1.1^12) ≈ 31,384.28
The value of the investment 12 years after purchase is predicted to be $31,384.28.
__
In any event, a graphing calculator or spreadsheet can deduce the model for you. The attached calculator output shows it to be as described above.


Jada made 8 cups of blueberry jam and divided the jam equally among 6 containers. How much jam went in each container?
Answers
Answer:
1.3 repeated is the answer
Answer:
Well if there is 8 cups and you want to divide it equally into 6 containers that would be 1.33 cups in each container
what is the equation of a line that passes through the points (2,5) and (4,3)
Answers
The equation of a line that passes through points (2,5) and (4,3) is
y = -x+7.
Finding the equation of a line:
First, we need to find out the slope for the given points.
(X1,Y1) = (2,5)
(X2,Y2) = (4,3)
formula for slope(m) = \(\frac{Y2 - Y1}{X2 - X1}\)
substitute the points in the above formula
\(\frac{3 - 5}{4 - 2}\) = \(\frac{-2}{2}\)
\(\frac{-2}{2}\) = -1
slope for the given points(m) = -1.
m = -1
The equation of a line is y-y1 = m(x-x1), where x and y are variables.
substituting the values in the above equation then :
y-5 = -1(x-2)
y-5 = -x+2
y+x = 2+5
x+y = 7
y = -x+7
Therefore, the equation of the line passing through the points (2,5) and (4,3) is y = -x+7
To solve more problems based on the linear equations:
https://brainly.com/question/9753782
Hello can someone help me with this please


Answers
Answer:
well there are eight total red cookies and there been two that had been bitten out of already that makes the ration 2:8
The product of a number and 3 increased by 9 is less than -42
TRANSLATE
Answers
Answer:
3x+9 < - 42
Step-by-step explanation:
The arc length of a sector is equal to one fourth of the radius. Express the arc length s as a function of the area a of the sector.
The arc length of a sector is equal to one fourth of the radius. Express the arc length s as a function of the area a of the sector.
Answers
In this relationship, the arc length is inversely Proportional to the area. As the area increases, the arc length decreases, and vice versa.
The relationship between the arc length (s) and the area (a) of a sector, let's start by understanding the formulas for each.
The arc length of a sector can be calculated using the formula:
s = θr
where s is the arc length, θ is the central angle of the sector in radians, and r is the radius.
The area of a sector can be calculated using the formula:
a = (1/2)θr^2
where a is the area, θ is the central angle of the sector in radians, and r is the radius.
Given that the arc length is equal to one fourth of the radius, we can express this relationship as:
s = (1/4)r
Now, let's express the central angle (θ) in terms of the area (a).
From the formula for the area of a sector, we can rearrange it to solve for θ:
a = (1/2)θr^2
Multiplying both sides by 2/r^2, we get:
2a/r^2 = θ
Substituting this value of θ back into the equation for the arc length (s), we have:
s = (1/4)r = (1/4)r(2a/r^2) = (1/2a)r
Therefore, we have expressed the arc length (s) as a function of the area (a) of the sector:
s = (1/2a)r
In this relationship, the arc length is inversely proportional to the area. As the area increases, the arc length decreases, and vice versa.
For more questions on Proportional .
https://brainly.com/question/29774220
#SPJ8
Help meeeeeeeeee I need the answer
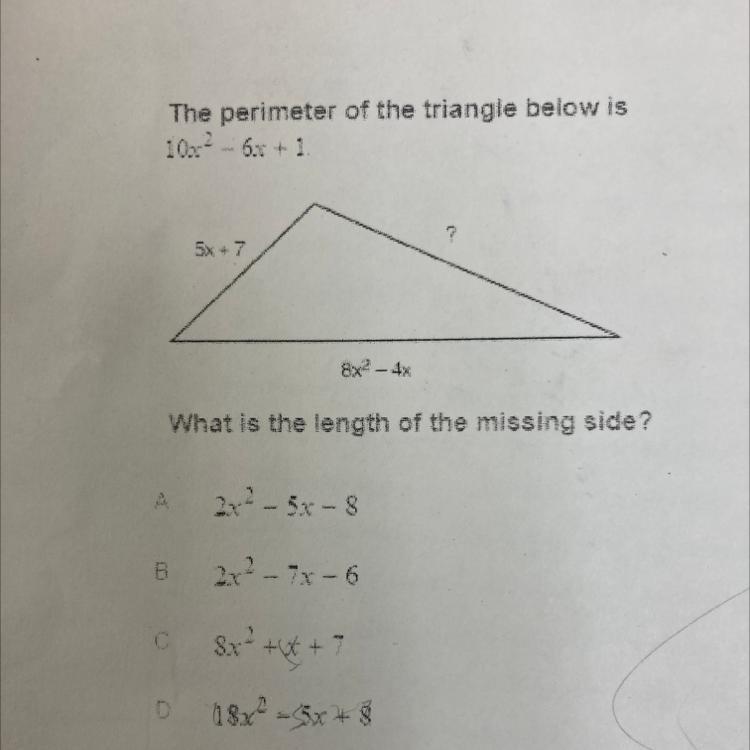
Answers
Answer:
d is the answer
Step-by-step explanation:
Answer:
B.
Step-by-step explanation:
\(?=(10x^{2} -6x+1)-(5x+7)-(8x^{2} -4x)\)
\(=10x^{2} -8x^{2} -6x-5x+4x+1-7\)
\(=2x^{2} -11x-4x-6\)
\(=2x^{2} -7x-6\)
Hope this helps
What is the image of (2,8) after a reflection over the line y = x?
PLS ANSWER FAST
Answers
Ended up getting the answer wrong because the other person this is the correct answer.
(8,2)
Enjoy and Happy Holidays :)
The image of (2,8) after a reflection over the line y = x is (8, 2).
The given coordinate is (2, 8).
What is a reflection over the line y=x?Reflect over the y = x: When you reflect a point across the line y = x, the x-coordinate and y-coordinate change places.
When we reflect (2, 8) over the line y=x, we get the coordinate as (8, 2). Because the x-coordinate and y-coordinate changed places.
Therefore, the image of (2,8) after a reflection over the line y = x is (8, 2).
To learn more about the reflection over the line y = x visit:
https://brainly.com/question/18376051.
#SPJ5
Evaluate log4 25 using common logarithms or natural logarithms. Round your answer to the nearest thousandth.
log4 25
Answers
Answer: 20 log (2)
Step-by-step explanation:
Answer: Logarithms are mathematical functions that are used to represent the relationship between two quantities that are related by a power law. For example, if we have an exponential equation like 2^x = 8, we can use logarithms to solve for x: log2 8 = x.
In general, logarithms are written in the form logb a, where b is the base of the logarithm and a is the number we want to take the logarithm of. There are several different bases in that logarithms can be written in, including the common logarithm (base 10) and the natural logarithm (base e).
To evaluate a logarithm, we need to use the logarithmic properties and the change of base formula. One important property of logarithms is that logb (xy) = logb x + logb y. Another property is that logb (x/y) = logb x - logb y.
The change of base formula is used when we need to evaluate a logarithm in a different base than the one given. The formula is:
logb a = logc a / logc b
where c is any base other than b or a. By using this formula, we can convert a logarithm from one base to another in order to evaluate it using a calculator.
In the case of log4 25, we can use the common logarithm (base 10) or the natural logarithm (base e) to evaluate the logarithm. Using the change of base formula with the common logarithm, we have:
log4 25 = log(25) / log(4)
Using a calculator, we find that log(25) ≈ 1.39794 and log(4) ≈ 0.60206, so:
log4 25 ≈ 1.39794 / 0.60206
Simplifying this expression, we get:
log4 25 ≈ 2.32193
Rounding to the nearest thousandth, we get:
log4 25 ≈ 2.322
So, the value of log4 25 to the nearest thousandth is 2.322.
Step-by-step explanation:
what is the inverse operation of multiply by 12 ?
Answers
Step-by-step explanation:
start with 12,multiply by 2 weeks get 24,now divide by 2 and we get back to 12
the following are the populations for the top twelve largest cities in the u. s. New York city, NY: 8,336,817 Los Angeles ca: 979.576 Chicago, il:2,693,976 Houston, Tx: 2,320,268 phoenix Az: 1,680,992 Philadelphia pa: 1,584,064 San Antonio Tx: 1, 547,253 San Diego ca: 1,423,851 Dallas Tx: 1,343,573 San Jose ca: 1,021,795 Austyn tx:978,908 Jacksonville Fl: 911,507. what is the mean population?, what is the median population?, what is the mode?, what is range?, what is the standard deviation?I need the standard deviation, I already did mode, mean, range, take the value of the population of each city, subtract the mode raised to 2, it does not give me the result
Answers
The mean is 2,071,798.33
The Median is 1,485,552
The range is 7,425,310
The standard deviation is given as 1961105.68
The mean population can be computed as:Mean = (Sum of all populations) / (Number of cities)
= (8,336,817 + 979,576 + 2,693,976 + 2,320,268 + 1,680,992 + 1,584,064 + 1,547,253 + 1,423,851 + 1,343,573 + 1,021,795 + 978,908 + 911,507) / 12
= 24,861,580 / 12
= 2,071,798.33
To find the median, we need to arrange the populations in increasing order and find the middle value. If we arrange these values, we get:
911,507, 978,908, 979,576, 1,021,795, 1,343,573, 1,423,851, 1,547,253, 1,584,064, 1,680,992, 2,320,268, 2,693,976, 8,336,817
Since there are 12 cities (an even number), the median would be the average of the 6th and 7th values:
Median = (1,423,851 + 1,547,253) / 2
= 1,485,552
The mode isn't applicable here as no city population repeats.
The range is the highest population minus the lowest population:
Range = 8,336,817 - 911,507
= 7,425,310
Standard deviation = (911507- 2068548.3333333)² + (978908 - 2068548.3333333)² + (979576 - 2068548.3333333)² + ( 1021795 - 2068548.3333333)² + (1343573- 2068548.3333333)² +( 1423851- 2068548.3333333)² + (1547253- 2068548.3333333)² +( 1584064- 2068548.3333333)² + (1680992- 2068548.3333333)² + ( 2320268- 2068548.3333333)² +(2693976- 2068548.3333333)² +( 8336817 - 2068548.3333333)² / 12
= 46151226311869 / 12
= 3845935525989.1
\(standard deviation = \sqrt{ 3845935525989.1}\)
= 1961105.6896529
Read more on mean , mode and median here https://brainly.com/question/14532771
#SPJ1
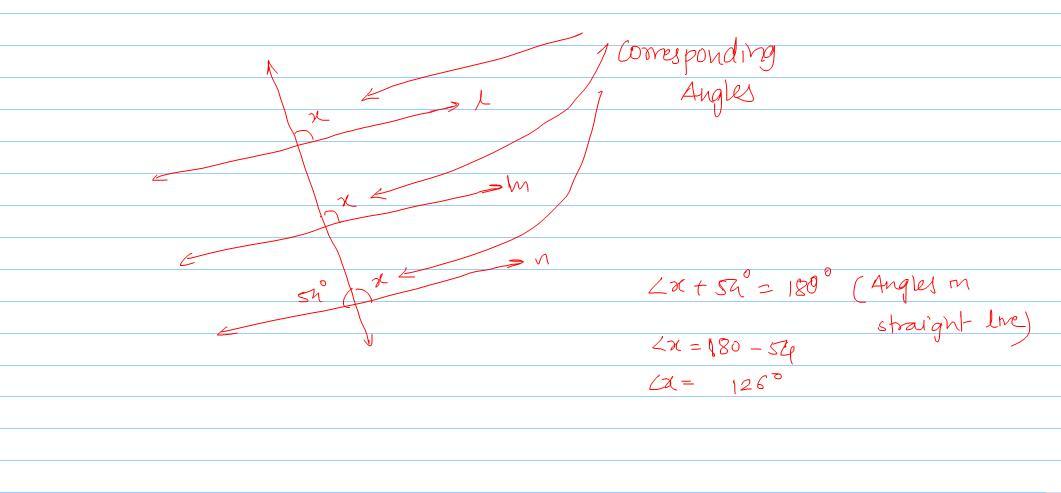
please help me thank you !!
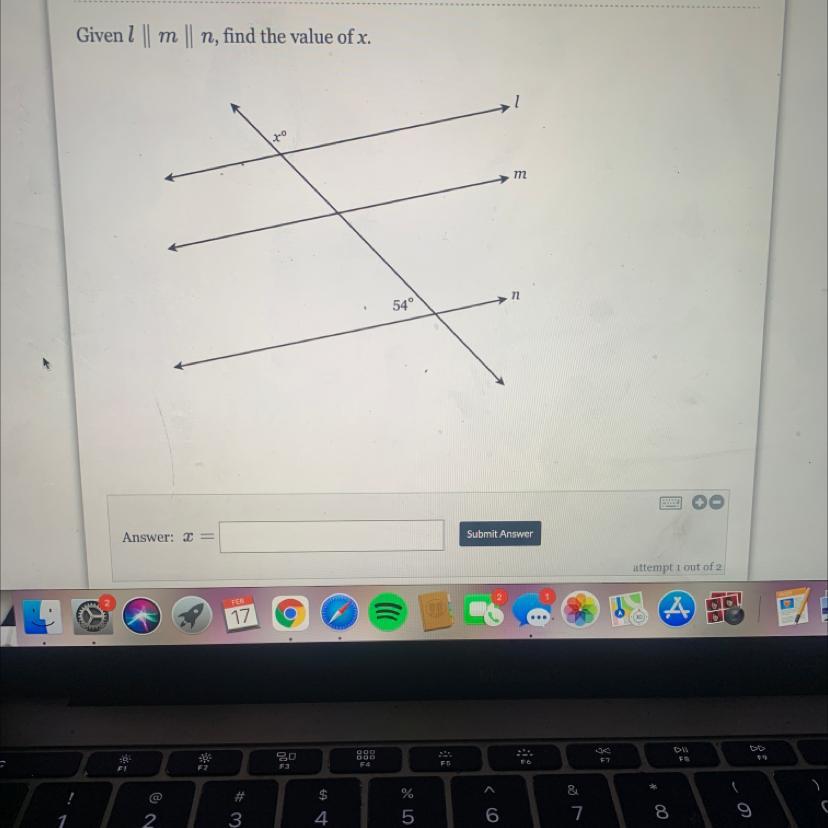
Answers
Answer:
126
Step-by-step explanation:
Calculate the mass of solid sodium acetate required to mix with 50.0 mL of 0.1 M acetic acid to prepare a pH 4 buffer.
Answers
The mass of solid sodium acetate required to mix with 50.0 mL of 0.1 M acetic acid to prepare a pH 4 buffer is 20.1 g
To prepare a pH 4 buffer, we need to use the Henderson-Hasselbalch equation
pH = pKa + log([A-]/[HA])
where pH is the desired pH, pKa is the dissociation constant of acetic acid (1.76), [A-] is the concentration of the acetate ion, and [HA] is the concentration of acetic acid
We can rearrange the Henderson-Hasselbalch equation to solve for the ratio of [A-]/[HA]
[A-]/[HA] = 10^(pH - pKa)
Substituting the given values, we have
[A-]/[HA] = 10^(4 - 1.76) = 48.937
We want to make a buffer by mixing solid sodium acetate with 50.0 mL of 0.1 M acetic acid. Let's assume that all of the acetic acid is converted to acetate ion and that the volume of the solution remains constant.
The number of moles of acetic acid in 50.0 mL of 0.1 M solution is
moles of acetic acid = 0.1 mol/L x 0.050 L = 0.005 mol
Since [A-]/[HA] = 48.937, the number of moles of acetate ion required to make the buffer is
moles of acetate ion = 48.937 x 0.005 mol = 0.245 mol
The molar mass of sodium acetate is 82.03 g/mol. To calculate the mass of solid sodium acetate required, we can use the following equation
mass of sodium acetate = moles of acetate ion x molar mass of sodium acetate
mass of sodium acetate = 0.245 mol x 82.03 g/mol = 20.1 g
Learn more about Henderson-Hasselbalch equation here
brainly.com/question/13423434
#SPJ4
Let f left parenthesis x right parenthesis equals x cubed minus x squared minus 1 and x subscript 0 equals 1 . To the nearest three decimal places, find x subscript 5 using Newton's method of approximation.

Answers
The value of \(x_5\), rounded to the nearest decimal place using Newton's method of approximation is 1.466.
The correct answer is option B.
To find the value of \(x_5\)using Newton's method of approximation, we need to iterate the following formula:
\(x_(_n_+_1_) = x_n - f(x_n) / f'(x_n)\)
where f'(x) represents the derivative of the function f(x). Let's calculate the values step by step.
Given function: f(x) = \(x^3 - x^2 - 1\)
Step 1: Find the derivative of f(x)
f'(x) = \(3x^2 - 2x\)
Step 2: Initialize the starting value
\(x_0\)= 1
Step 3: Calculate \(x_1\)
\(f(x_0) = f(1) = (1^3) - (1^2) - 1 = 1 - 1 - 1 = -1\)
\(f'(x_0) = f'(1) = (3(1^2)) - (2(1)) = 3 - 2 = 1\)
\(x_1 = x_0 - f(x_0) / f'(x_0)\)
= 1 - (-1) / 1
= 2
Step 4: Calculate \(x_2\)
\(f(x_1) = f(2) = (2^3) - (2^2) - 1 = 8 - 4 - 1 = 3\)
\(f'(x_1) = f'(2) = (3(2^2)) - (2(2)) = 12 - 4 = 8\)
\(x_2 = x_1 - f(x_1) / f'(x_1)\)
= 2 - 3 / 8
= 1.625
Step 5: Repeat the process until we reach \(x_5\)
Performing the calculations for \(x_3, x_4, andx_5\), we find:
\(x_3\) ≈ 1.465
\(x_4\) ≈ 1.466
\(x_5\)≈ 1.466
After applying Newton's method of approximation to the function f(x) = \(x^3 - x^2 - 1,\)starting with,\(x_0 = 1,\) we iteratively calculated the values of \(x_1, x_2, x_3, x_4, and x_5\). The final approximation, \(x_5\), is approximately 1.466 when rounded to the nearest decimal place. This aligns with option B as the correct answer.
For more such information on: Newton's method of approximation
https://brainly.com/question/31400694
#SPJ8
I need help quick !!!!!!!!!!!!!!!!!!!!!!

Answers
Answer:
192ft squared. But remember it says don't put the square feet so just type in: 192.
Step-by-step explanation:
The top triangle is 42 ft squared.
The rectangle below it is 150 feet squared.
You add them together and get 192 ft squared hope this helps!
8. Write a paragraph proof.
Proof Given: In a plane, a is perpendicular to b, b id perpendicular to c, and c || d.
Prove: a || d
Answers
To prove that line segment a is parallel to line segment d, based on the given information, we can utilize the properties of perpendicular and parallel lines.
Given that a is perpendicular to b and b is perpendicular to c, we know that angles formed between a and b, as well as between b and c, are right angles. Let's denote these angles as ∠1 and ∠2, respectively.
Now, since c is parallel to d, we can conclude that the corresponding angles ∠2 and ∠3, formed between c and d, are congruent.Considering the fact that ∠2 is a right angle, it can be inferred that ∠3 is also a right angle.
By transitivity, if ∠1 is a right angle and ∠3 is a right angle, then ∠1 and ∠3 are congruent.Since corresponding angles are congruent, and ∠1 and ∠3 are congruent, we can deduce that line segment a is parallel to line segment d.
Thus, we have successfully proven that a is parallel to d based on the given information and the properties of perpendicular and parallel lines.
For more such questions on line segment
https://brainly.com/question/30756145
#SPJ8
A fruit basket contains 3 mangoes 4 oranges and 3 apples. Another fruit basket contains 5 mangoes, 5 oranges and 5 apples. One basket is selected at random. 1. what is the probabilities that both are mangoes?
Answers
If one basket is selected at random, the probability that both are mangoes is; 1/10
How to find probabilities?
Contents of first basket;
3 mangoes
4 oranges
3 apples
Contents of second basket;
5 mangoes.
5 oranges.
5 apples.
Probability of mango in first basket is = 3/10
Probability of mango in second basket is = 5/15
Thus;
Probability that both are mangoes = (3/10) * (5/15)
Probability that both are mangoes = 1/10
Read more about Probabilities at; https://brainly.com/question/24756209
#SPJ1
Correct answer please

Answers
Answer:
50.75
Step-by-step explanation:
We have:
\(E[g(x)] = \int\limits^{\infty}_{-\infty} {g(x)f(x)} \, dx \\\\= \int\limits^{1}_{-\infty} {g(x)(0)} \, dx+\int\limits^{6}_{1} {g(x)\frac{2}{x} } \, dx+\int\limits^{\infty}_{6} {g(x)(0)} \, dx\\\\= \int\limits^{6}_{1} {g(x)\frac{2}{x} } \, dx\\\\=\int\limits^{6}_{1} {(4x+3)\frac{2}{x} } \, dx\\\\=\int\limits^{6}_{1} {(4x)\frac{2}{x} } \, dx + \int\limits^{6}_{1} {(3)\frac{2}{x} } \, dx\\\\=\int\limits^{6}_{1} {8} \, dx + \int\limits^{6}_{1} {\frac{6}{x} } \, dx\\\\\)
\(=8\int\limits^{6}_{1} \, dx + 6\int\limits^{6}_{1} {\frac{1}{x} } \, dx\\\\= 8[x]^{^6}_{_1} + 6 [ln(x)]^{^6}_{_1}\\\\= 8[6-1] + 6[ln(6) - ln(1)]\\\\= 8(5) + 6(ln(6))\\\\= 40 + 10.75\\\\= 50.74\)
How far above ground is the top of the pole?

Answers
Answer:
I would say about 7 feet and 1 inch
Step-by-step explanation:
Pls Answer The following Question Given

Answers
Answer:
11/15 > 4/7.
Step-by-step explanation:
11/15 = 0.7333.....
4/7 = 0.5714....
Obviously from this, we can conclude that 11/15 is greater than 4/7.
So, the answer is 11/15 > 4/7.
Answer:
a)>
hope it's helpful ❤❤❤
THANK YOU.

A cyclist rides her bike at a speed of 18 miles per hour. What is this speed in kilometers per hour? How many kilometers will the cyclist travel in 2 hours? In
your computations, assume that I mile is equal to 1 kilometers. Do not round your answers.
Speed: ___km/h
Distance traveled in 2 hours :
__km
Answers
Answer: 110
Step-by-step explanation:
Answer:
Step-by-step explanation: