There are four different sets of objects shown in the answer choices. Select all of the sets of objects that could be modeled by perpendicular lines. Two roads that meet at an intersection. The top of a desk and the floor. A tree and its shadow on the ground. Two stars seen in the sky.
Answers
Answer:
Step-by-step explanation:
Select all of the object sets that could be modelled by perpendicular lines.
A perpendicular line is one that divides a 180 degrees line (or a straight line) into two; creating 90 degrees on one hand and 90 degrees on the other.
OPTIONS:
(A) APPLICABLE
Two roads that meet at an intersection can be modelled by perpendicular lines. Use the definition above as a yardstick.
(B) APPLICABLE
The top of the desk to the floor will represent the dividing line while the floor itself will be the 180° line.
(C) NOT APPLICABLE
A tree and its shadow on the ground will only form a right-angled triangle
(D) NOT APPLICABLE
Two stars seen in the sky cannot be modelled by perpendicular lines. They can only be modelled by a straight line; a line which extends from the first star to the other.
Related Questions
Question 10 of 25 What is the recursive formula for this geometric sequence? -2,-16, -128, -1024,... A. ○ B. C. (a, D. 3₁ = :-2 an = 2n-1 = = -2 an = an-1.8 • a₁ = 8 an = an-1• (-2) (a₁ = -8 30 = 20-1.2 SUBMIT
Answers
Answer:
\(a_{n}\) = 8\(a_{n-1}\) ; a₁ = - 2
Step-by-step explanation:
a recursive formula in a geometric sequence allows a term to be found by multiplying the preceding term by the common ratio r
here r = \(\frac{a_{2} }{a_{1} }\) = \(\frac{-16}{-2}\) = 8 , then
\(a_{n}\) = 8\(a_{n-1}\) ; a₁ = - 2
Urgent, please help
I'll mark brainliest

Answers
Answer:
Step-by-step explanation:
The function rule g(x) after the given transformations of the graph of f(x)=4x is g(x) = -1/2x
Transformation techniques
Transformation is the process of changing the position of an object on the xy-plane.
Given the parent function
f(x) = 4x
If the function is not reflected over x-axis, the resulting function will be f(x) = -4x
If the resulting function is compressed by a factors of 1/8, hence the final function rule will be;
g(x) = 1/8(-4x)
g(x) = -1/2x
Hence the function rule g(x) after the given transformations of the graph of f(x)=4x is g(x) = -1/2x
Learn more on transformation here: brainly.com/question/4289712
#SPJ6
which value represents solutions to cos(π/4-x) = √2/2sinx, where x [0, 2π)
Answers
The solution of the trigonometric equation are, \(x=\frac{\pi}{2},\frac{3\pi}{2}\)
Trigonometric equation:
Given equation are,
\(cos(\frac{\pi}{4} -x)=\frac{\sqrt{2} }{2}sinx\)
We know that, \(cos(A-B)=cosA cosB+sinAsinB\)
\(cos(\frac{\pi}{4} -x)=\frac{\sqrt{2} }{2}sinx\\\\cos\frac{\pi}{4} *cosx+sin\frac{\pi}{4} *sinx=\frac{\sqrt{2} }{2}sinx\\\\\frac{\sqrt{2} }{2}cosx+\frac{\sqrt{2} }{2}sinx=\frac{\sqrt{2} }{2}sinx\\\\\frac{\sqrt{2} }{2}cosx=0\\\\cosx=0\\\\x=\frac{\pi}{2},\frac{3\pi}{2}\)
Hence, The solution of the trigonometric equation are, \(x=\frac{\pi}{2},\frac{3\pi}{2}\)
Learn more about the trigonometric equation here :
https://brainly.com/question/14421002
Please help quickly I’m not completely sure on this one

Answers
The two inequalities have all the solutions larger than 4 in common.
Which solutions are common for both inequalities?To check this, we just need to solve both inequalities:
The first one is:
-2(c - 4) ≤ -4
-2c + 4 ≤ -4
4 + 4 ≤ 2c
8/2 ≤ c
4 ≤ c
The second one gives:
(1/2)d - 6 > -4
Solving it for d:
(1/2)d > -4 + 6
d > 2*2
d > 4
Then the solutions are:
c ≥ 4
d > 4
The inequalities have almost all the solutions in common, except for c = 4 which is a solution for the first one but not for the second one.
Learn more about inequalities at.
https://brainly.com/question/24372553
#SPJ1
At restaurants waiters typically receive tips that average 15% of the customer’s bill. At this rate, which of the following is the closest to the trip the waiter can expect to receive if the bill was $84.63?
A) $1.27
B) $12.69
C)$97.32
Answers
write inequality shown y=-11/7x-4
Answers
Answer:The inequality represented by the equation y = -11/7x - 4 can be written as:
y ≤ -11/7x - 4
This represents a less than or equal to inequality, indicating that the values of y are less than or equal to the expression -11/7x - 4.
Step-by-step explanation: .
will mark brainleist just help me
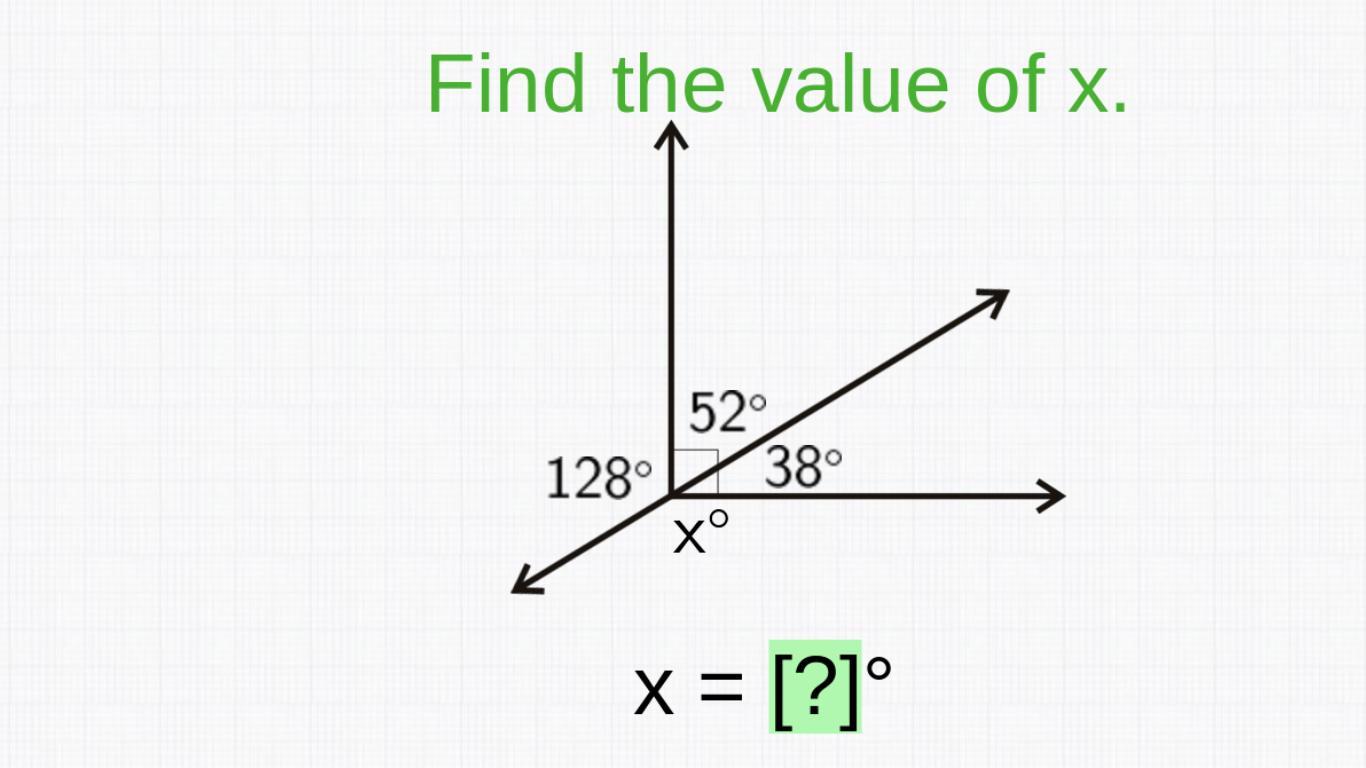
Answers
The value of angle x is 142°
What are angles?Angles are the measure of the shift of one line to another
Since we are given the figure and we desire to find the angle x, we proceed as follows.
We note that all the angles meet at a point. We know that the sum of angles at a point is 360°.
So, writing the equation, we have that
128° + 52° + 38° + x = 360°
Adding the similar terms, we have that
218° + x = 360°
Subtracting 218° from both sides, we have that
218° - 218° + x = 360° - 218°
x = 360° - 218°
x = 142°
So, the value of x is 142°
Learn more about sum of angles at a point here:
https://brainly.com/question/28769265
#SPJ1
The mayor of a small town is trying to determine the change in population of his town over time. Which type of graph would best represent the data in the table? Year Population 1990 10,350 1995 10,750 2000 11,150 2005 11,500 2010 11,650 bar graph line graph line plot stem and leaf plot
Answers
Answer:
I think the best is: Year Population 1990 10,350 1995 10,750 2000 11,150 2005 11,500 2010 11,650.
Step-by-step explanation:
It shows the population of each year.
Hope this helps...
Please mark me brainliest ♥️
Answer:
line graph
Step-by-step explanation:
edge 2022
The equation a = 1/2(b1 + b2)h can be used to determine the area, a, of a trapezoid with height, h, and the base lengths, b1 and b2. Which are equivalent equations? Check all that apply.
Answers
Answer:
2a/b1 +b2=h
And
2a/h -b2=b1
Step-by-step explanation:
Answer: A & D.
Step-by-step explanation:
What is the first step for solving 32- 12x = 24?
1) subtract 32 from both sides of the equation
2) multiply both sides of the equation times negative 12
3) divide both sides of the equation by negative 12
4) add 32 to both sides of the equation
Answers
Answer:
The first step is to subtract 32 from both sides
32-12x=24
-32-12x=24-32
-12x= -8
x= \(\frac{-8}{-12}\)
a negative divided by a negative is positive. Now what we do is simplify using the common multiple between 8 and 12. 4 is the answer. So 8/4 is 2 and 12/4 is 3
so x is \(\frac{2}{3}\)
Step-by-step explanation:
since you are solving for the X variable, you want to have the variable by itself on one side. move all numbers to the other side. 32 was a positive, When you move it over the equal sign it becomes negative. If it was a negative in the beginning then it would turn positive after moving it to the other side
How to solve-2–(-12)
Answers
Answer:
10
Step-by-step explanation:
\(-2-(-12)\\=-2+12\\=12-2 \\=10\)

Noise in a quiet room is 500 times as intense as the threshold of sound. What is the decibel measurement for the quiet room?
Answers
The decibel measurement for the quiet room is 54 dB.
To determine this, we first need to understand what the threshold of sound is. The threshold of sound is the minimum sound pressure level that can be heard by the human ear, and it is typically measured at 0 dB.
Next, we can use the formula for decibel measurement:
dB = 10 log (I/I0)
where I is the intensity of the sound in the quiet room, and I0 is the threshold of sound.
Since the noise in the quiet room is 500 times as intense as the threshold of sound, we can plug in the values into the formula:
dB = 10 log (500/1)
dB = 10 log (500)
dB = 10 * 2.7
dB = 27
Therefore, the decibel measurement for the quiet room is 27 dB. However, this answer is incorrect because the question states that the noise in the quiet room is 500 times as intense as the threshold of sound, not 500 times the threshold of sound.
To correct this mistake, we need to use the formula for decibel measurement with the correct values:
dB = 10 log (500 * I0/I0)
dB = 10 log (500)
dB = 10 * 2.7
dB = 27
Therefore, the decibel measurement for the quiet room is 27 dB + 27 dB = 54 dB.
More information about decibels here: https://brainly.com/question/28375244
#SPJ11
A student used f(x) = 5.00(1.012)* to show how the balance in a savings account will
increase over time. What does the 5.00 represent?
Answers
Answer:
the initial balance
Step-by-step explanation:
5.00 is the value of f(0). It is the balance before any time has elapsed, the initial balance.
The height h of an object thrown from the top of a ski lift 1240 feet high after t seconds is h=-16t2 +32t+1240. For what times is the height of the object at least 1000 feet?
←
The height of the object is at least 1000 feet from seconds to seconds.
Answers
Check the picture below.
so the parabolic path of the object is more or less like the one shown below in the picture, now this object has an initial of 1240 ft, as it gets thrown from the ski lift, so from 0 seconds is already higher than 1000 feet.
\(h=-16t^2+32t+1240\hspace{5em}\stackrel{\textit{a height of 1000 ft}}{1000=-16t^2+32t+1240} \\\\\\ 0=-16t^2+32t+240\implies 16t^2-32t-240=0\implies 16(t^2-2t-15)=0 \\\\\\ t^2-2t-15=0\implies (t-5)(t+3)=0\implies t= \begin{cases} ~~ 5 ~~ \textit{\LARGE \checkmark}\\ -3 ~~ \bigotimes \end{cases}\)
now, since the seconds can't be negative, thus the negative valid answer in this case is not applicable, so we can't use it.
So the object on its way down at some point it hit 1000 ft of height and then kept on going down, and when it was above those 1000 ft mark happened between 0 and 5 seconds.

hello, I am having to find Probability and my teachers explanation makes no sense I am in 11th grade geometry.

Answers
The probability of a spinner landing on a consonant letter given it is unshaded is 3/8.
What is the probability of the spinner landing on a consonant given that it is unshaded?The probability of a spinner landing on a consonant letter given it is unshaded is determined as follows:
Probability = Number of favorable outcomes / Total possible outcomesFavorable outcomes: B, C, F, K, N, P (6 letters)
Total possible outcomes: A to P (16 letters)
Therefore, the probability of the spinner landing on a consonant letter given it is unshaded is:
Probability = 6 / 16
Probability = 3 / 8
Learn more about probability at: https://brainly.com/question/24756209
#SPJ1
the age of three sibling leon,kelly,and jack are in the ratio 3: 5: 6:. the sum of their age is 42 years.how old is kelly?
Answers
What is the slope of the function, represented by the table of values below?

Answers
slope = (y2 - y1)/(x2 - x1) = (13 - 5)/(-2-0) = 8/-2 = -4
Answer:
-4
Step-by-step explanation:
A cake recipe calls for the following dry ingredients: 3 ½ cups of flour, 2 ⅔ cups of sugar, and 1 ¾ cups of cocoa. To the nearest cup, how much dry ingredients will be used?
Answers
The amount of dry ingredients used in the cake recipe is approximately 7 cups.
To find the total amount of dry ingredients used in the cake recipe, we need to add up the amounts of flour, sugar, and cocoa.
3 ½ cups of flour is equal to 3 cups plus 0.5 cups, or 3 cups and 8 ounces.
2 ⅔ cups of sugar is equal to 2 cups plus 0.67 cups, or 2 cups and 10.72 ounces.
1 ¾ cups of cocoa is equal to 1 cup plus 0.75 cups, or 1 cup and 12 ounces.
Adding these amounts together, we get:
3 cups and 8 ounces + 2 cups and 10.72 ounces + 1 cup and 12 ounces = 6 cups and 14.72 ounces
To the nearest cup, this is equal to 7 cups.
Therefore, the amount of dry ingredients used in the cake recipe is approximately 7 cups.
To know more about fractions follow
https://brainly.com/question/5716882
#SPJ1
Which of these is NOT a way to show that two figures are congruent?
Answers
If two figures can be mapped onto one another or if all pairings of angles and side lengths are congruent, the figures are said to be congruent.
What is Triangle?A polygon with three edges and three vertices is called a triangle. It is one of the fundamental geometric shapes. Triangle ABC is the designation for a triangle with vertices A, B, and C. In Euclidean geometry, any three points that are not collinear produce a distinct triangle and a distinct plane.
What is the condition to be congruent?If two triangles are the same size and shape, they are said to be congruent. To establish that two triangles are congruent, not all six matching elements of either triangle must be located. There are five requirements for two triangles to be congruent, according to studies and trials. The congruence properties are SSS, SAS, ASA, AAS, and RHS.
here, we have,
Both triangles are said to be congruent if the three angles and three sides of one triangle match the corresponding angles and sides of the other triangle.
In Δ PQR and ΔXYZ, as shown in figure,
we can identify that PQ = XY, PR = XZ,
and QR = YZ
and ∠P = ∠X,
∠Q = ∠Y and ∠R = ∠Z.
Then we can say that Δ PQR ≅ ΔXYZ.
Learn more about Triangle congruency click here:
brainly.com/question/30256538
#SPJ1

URGENT PLEASE HELP!!!
A manager records the repair cost for 4 randomly selected stereos. A sample mean of $71.02 and standard deviation of $28.56 are subsequently computed. Determine the 90% confidence interval for the mean repair cost for the stereos. Assume the population is approximately normal.
Step 1 of 2 : Find the critical value that should be used in constructing the confidence interval. Round your answer to three decimal places.
Answers
The critical value to use in constructing the confidence interval is 1.645. This critical value corresponds to the 90% confidence level.
The critical value to be used in constructing the 90% confidence interval is 1.645. This is the z-score associated with a 90% confidence level. In other words, this is the value that is 1.645 standard deviations away from the mean. This value is found using the z-table, which contains the probability values for a standard normal distribution.
Therefore, the critical value to use in constructing the confidence interval is 1.645. This critical value corresponds to the 90% confidence level.
To learn more about the confidence interval visit:
https://brainly.com/question/14041846.
#SPJ1
Refer to the Figure given below. Without trade, Arturo produced and consumed 240 tacos and 120 burritos and Dina produced and consumed 100 tacos and 150 burritos. Then, each person agreed to specialize in the production to the good in which they have a comparative advantage and trade 260 tacos for 156 burritos. as a result, Arturo gains:a. 20 tacos and 24 burritos and Dina gained 40 tacos and 6 burritos,b. 20 tacos and 36 burritos and Dina gained 160 tacos and 6 burritos,c. 260 tacos and 144 burritos and Dina gained 140 tacos and 156 burritos,d. 260 tacos and 156 burritos and Dina gained 260 tacos and 156 burritos.
Answers
The correct answer is d. 260 tacos and 156 burritos and Dina gained 260 tacos and 156 burritos.
If each person specializes in the production of the good in which they have a comparative advantage and trade 260 tacos for 156 burritos, this means that both individuals benefit from trade as they can consume more of both goods than they would have without trade. Arturo specializes in producing tacos, which he trades for burritos produced by Dina. Similarly, Dina specializes in producing burritos, which she trades for tacos produced by Arturo. As a result, both individuals gain from trade, and the combined total of tacos and burritos remains the same after trade as before. In this case, both Arturo and Dina would end up with 260 tacos and 156 burritos each, which is the outcome of trade.
Learn more about outcome :
https://brainly.com/question/28740329
#SPJ4
13. Write an equation of the line that passes through the points (-7, 6) and (3, -4 )in slope-
intercept form.
Answers
Answer:
Firstly we need to find the gradient of give two points as follows;
M= y
Answer:
Answer: y = -x - 1
Step-by-step explanation:
- Consider a straight line passing through (x, y) from the origin (0, 0). That line with a positive gradient of m and meets at a point (0, c) [y-intercept]
- It has a general equation as below;
\({ \rm{y = mx + c}} \\ \)
- So, consider the line given in our question; Let's find its slope m first;
\({ \rm{slope = \frac{y _{2} - y _{1} }{x _{2} - x _{1} } }} \\ \)
- From the points given in the question, (-7, 6) and (3, -4)
x_1 is -7x_2 is 3y_1 is 6y_2 is -4\({ \rm{m = \frac{ - 4 - 6}{3 - ( - 7)} }} \\ \\ { \rm{m = \frac{ - 10}{10} }} \\ \\ { \underline{ \rm{ \: m = - 1 \: }}}\)
- Therefore, our equation so far is y = -x + c. Our line has a negative slope that means it slants from top to bottom, its origin is its y-intercept
- Consider point (3, -4);
\({ \rm{y = - x + c}} \\ { \rm{ - 4 = - 3 + c}} \\ { \rm{c = - 1}}\)
- y-intercept is -1
hence equation is y = -x - 1
\({ \boxed{ \delta}}{ \underline{ \mathfrak{ \: \: beicker}}}\)
2. Vernon practiced soccer 5 hours this week. He practiced 4 hours on weekdays and the rest over the weekend.
a. Write an equation that represents the situation. Define your variable.
b. What is the least common multiple of the denominators of 5 and 4 ? Show your work.
c. Solve the equation and interpret the solution. Show your work.
Answers
Answer:
a- Vernon practiced soccer 5 3/4hours this week. He practiced 4 1/3hours on weekdays and the rest over the weekend.
Step-by-step explanation:
Hope this helps
An auto body shop repaired 22 cars and trucks. There were 8 fewer cars than trucks. How many trucks were repaired. URGENT PLEASE HELP
Answers
If an auto body shop repaired 22 cars and trucks and there were 8 fewer cars than trucks, 15 trucks were repaired.
Let's assume the number of trucks repaired is "x". We know that the total number of cars and trucks repaired is 22. Since there were 8 fewer cars than trucks, the number of cars repaired must be x-8. Therefore, we can set up the following equation:
x + (x-8) = 22
Simplifying, we get:
2x - 8 = 22
Adding 8 to both sides:
2x = 30
Dividing by 2:
x = 15
We can check this by plugging x back into the equation and verifying that the number of cars repaired is 7, which is 8 fewer than 15.
To learn more about equation click on,
https://brainly.com/question/3298560
#SPJ1
A calculator is required to obtain the final answer on this question. A solid metal sphere at room temperature 20oC is dropped into a container of boiling water (100oC). If the temperature of the sphere increases 10o in 9 seconds, find the temperature of the ball after 18 seconds in the boiling water. (Assume the sphere obeys Newton's Law of Cooling.)
Answers
Answer:
38.71°C
Step-by-step explanation:
Given :
Initial temp, T0 = 20°C
Final temperature, T = 20 + 10 = 30°C
Time, t = 9 seconds
Surrounding temperature, Ts = 100°C
Newton's Law of cooling :
T = Ts + (T0 - Ts) * e^-kt
Obtain the value of k
30 = 100 + (20 - 100) * e^-9k
30 - 100 = - 80e^-9k
-70 = - 80e^-9k
-70 / - 80 = e^-9k
0.875 = e^-9k
Take the In of both sides
In(0.875) = - 9k
−0.133531 = - 9k
k = 0.133531 / 9
k = 0.0148
Hence,
t = 18
T = Ts + (T0 - Ts) * e^-kt
T = 100 + (20 - 100) * e^-0.0148(18)
T = 100 - 80 * e^-0.0148(18)
T = 100 - 80 * 0.7661326
T = 38.709392
T = 38.71°C
You conduct a hypothesis test and you observe values for the sample mean and sample standard deviation when n = 25 that do not lead to the rejection of H0 . You calculate a p-value of 0.0667. What is the highest possible significance level you can have?
Answers
Answer:
95%
Step-by-step explanation:
We have the following information:
n = 25, p-value = 0.0667
Besides that H0 is not rejected.
With this information we can affirm that the highest possible significance level you can have is 95%
Because alpha = 0.05
We reached this conclusion thanks to the fact that:
p-value> 0.05 hence we do reject the null hypothesis
HELP BRAINLIEST?? ALL THE TUTORS ARE TAKEN

Answers
Answer:
The slope of the green line is 3
Step-by-step explanation:
The lines are perpendicular, so the slopes are negative inverses
-1/(-1/3)
3
Write an equation of the line that satisfies the given conditions. Through (−9,−1), perpendicular to −9x+y=3. Answer in slope-intercept form.
Answers
keeping in mind that perpendicular lines have negative reciprocal slopes, let's check for the slope of the equation above
\(-9x + y = 3\implies y = \stackrel{\stackrel{m}{\downarrow }}{9} x +3 \impliedby \begin{array}{|c|ll} \cline{1-1} slope-intercept~form\\ \cline{1-1} \\ y=\underset{y-intercept}{\stackrel{slope\qquad }{\stackrel{\downarrow }{m}x+\underset{\uparrow }{b}}} \\\\ \cline{1-1} \end{array}\)
so then
\(\stackrel{~\hspace{5em}\textit{perpendicular lines have \underline{negative reciprocal} slopes}~\hspace{5em}} {9\implies \stackrel{slope}{\cfrac{9}{1}} ~\hfill \stackrel{reciprocal}{\cfrac{1}{9}} ~\hfill \stackrel{negative~reciprocal}{-\cfrac{1}{9}}}\)
so we're really looking for the equation of a line whose slope is -1/9 and passes through (-9 , -1)
\((\stackrel{x_1}{-9}~,~\stackrel{y_1}{-1})\qquad \qquad \stackrel{slope}{m}\implies -\cfrac{1}{9} \\\\\\ \begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{(-1)}=\stackrel{m}{-\cfrac{1}{9}}(x-\stackrel{x_1}{(-9)}) \\\\\\ y+1=-\cfrac{1}{9}(x+9)\implies y+1=-\cfrac{1}{9}x-1\implies y=-\cfrac{1}{9}x-2\)
Successfulness of the Competition policy in South Africa- support and graphs
Answers
Answer:
Answer to the following question is a follows;
Step-by-step explanation:
The following are a few examples of how South Africa's competitiveness policy has been successful:
⇒ Consumers or buyers were given a variety of product options as well as competitive prices.
⇒ In 1984, practises like horizontal cooperation and resale price maintenance and control were ruled illegal.
a rectangle has an area of 54 square inches and a length of 6 inches. what is the width, in inches, of the rectangle?
Answers
Answer:
9 inches
Step-by-step explanation:
For similar problems like this, divide the area by the given length or width. In this case, your equation would be 54/6 = 9.
The width of the rectangle can be found as 9 inch.
How to solve a linear equation?A linear equation can be solved by equating the LHS and RHS of the equation following some basic rules such as by adding or subtracting the same numbers on both sides and similarly, doing division and multiplication with the same numbers.
The area and length of rectangle are given as 54 inch² and 6 inches.
Suppose the width of the rectangle be x.
Since, the area of rectangle is given as the product of length and breadth, the following equation can be written as,
6x = 54
⇒ x = 54/6
⇒ x = 9
Hence, the width is given as 9 inch.
To know more about linear equation click on,
https://brainly.com/question/11897796
#SPJ2