Answers
Answer:
Across
Evapotranspiration is the sum of evaporation from plants.
Earth is surrounded by invisible gases that form a thin protective blanket that we call the atmosphere.
Water flows downhill because gravity is a form of potential energy – and the water, or anything that falls or rolls downward – flows in response to differences in potential energy (from high to low). ... Therefore, the potential energy that drives groundwater movement includes both pressure and gravity.
Precipitation: hail, rain, freezing rain, sleet and snow.
Condensation is the opposite of vaporization. Condensation occurs when a gas loses energy, slows in motion so that its cohesive force pulls the molecules close, but the molecules still have enough energy to break away from one connection only to connect with another molecule.
Down
Alternatively evaporation of the liquid should leave a solid residue. ... Dissolving is a reversible process and the solute can be recovered from a solution by evaporation though it will not always be in the exactly the same form as at the start.
Boiling. If a liquid is heated the particles are given more energy and move faster and faster expanding the liquid.
Answer: No entiendo la historia y no vengas por mí, solo quería los puntos jajaja
Step-by-step explanation:
Related Questions
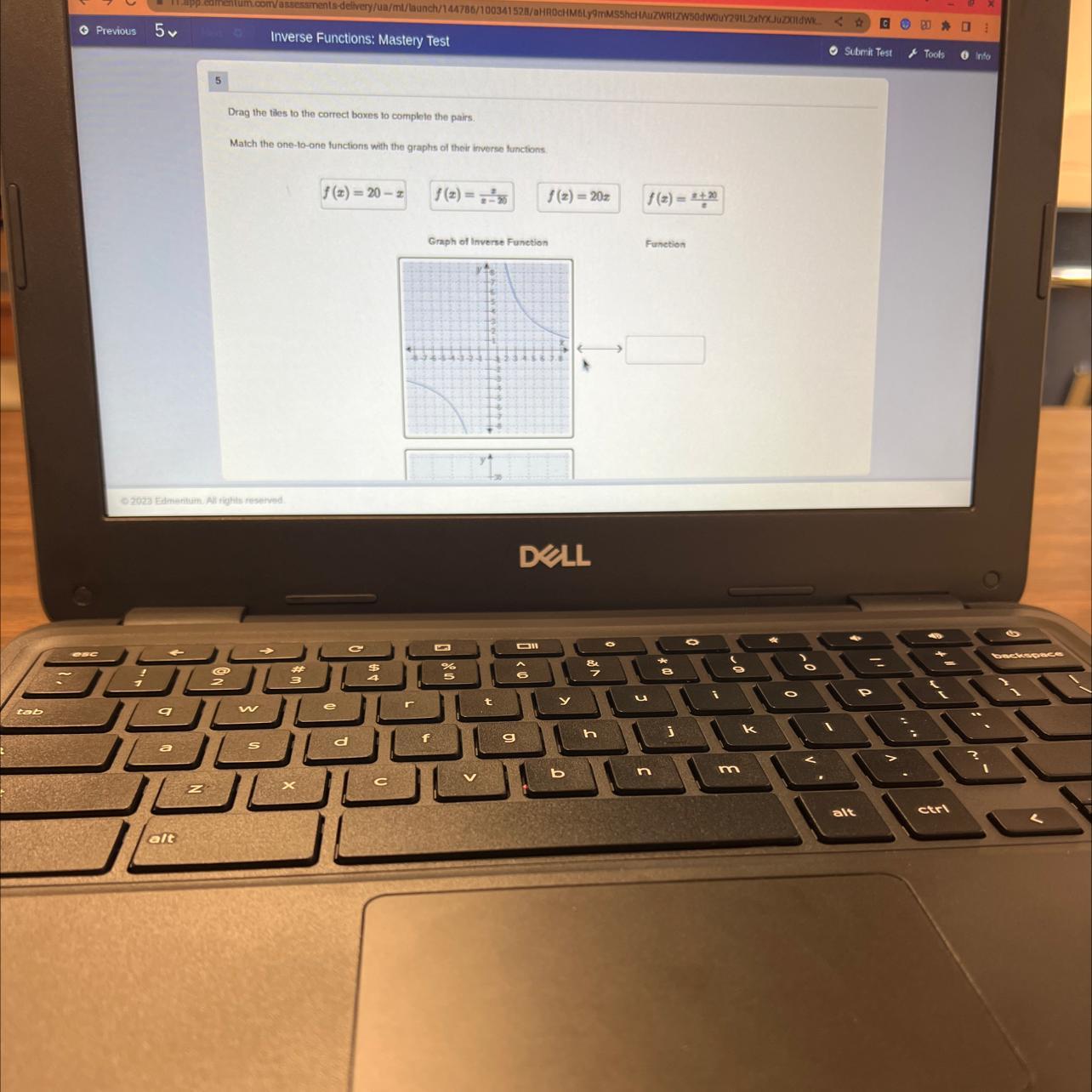
Has anyone done the inverse functions mastery text on edmentum it’s super hard stuck on this question and the pictures wont help
Answers
Find the standard form of the equation of the circle with center (-5,3) and tangent to the line y = 1.
Answers
Answer:
( x + 5 )^2 + ( y - 3 )^2 = 2^2
Step-by-step explanation:
The equation for a circle is ( x - h )^2 + ( y - k )^2 = r^2.
We know that h=-5 and k=3, so we just need to solve for r.
To do that, we need to envision the circle on a graph. If the edge of the circle touches the horizontal line y=1, how many units is it between the edge of the circle and the middle of the circle?
The middle of the circle is at y=3, and the edge is at y=1, so there are 2 units between the edge and the middle. Which means r=2.
so, ( x + 5 )^2 + ( y - 3 )^2 = 2^2.
The town of Valley View conducted a census this year, which showed that it has a population
of 1,800 people. Based on the census data, it is estimated that the population of Valley View
will grow by 12% each decade.
Write an exponential equation in the form y = a(b) that can model the town population, y, x
decades after this census was taken.
Use whole numbers, decimals, or simplified fractions for the values of a and b.
Answers
Answer:
ytlyguk
Step-by-step explanation:
gghfhfdh
if you invest $550.00 and your annual interest is 4%, what will be the interest
Answers
The annual interest is $22.
What is simple interest?Simple interest is a method of calculating the interest charge. Simple interest can be calculated as the product of principal amount, rate and time period.
Simple Interest = (Principal × Rate × Time) / 100
Given;
Amount invested= $550
Annual interest= 4%
SI= 550*4*1/100
=5.5*4
=22
Therefore, the simple interest will be $22.
Learn more about simple interest here;
https://brainly.com/question/1548909
#SPJ1
M=3n/4 if n=8 find M
Answers
Answer:
\(M=6\)
Step-by-step explanation:
\(M=\frac{3\cdot8}{4}\)
Solve
Step 1: Multiply the numbers
\(3\cdot \:8=24\)
Step 2: Divide
\(\frac{24}{4}=6\)
\(M=6\)
Why are there two solutions for the equation |6 + y| = 2?
Answers
Answer:
it can be negative or positive. You can change the number after the equal to a negative, or a positive depending on what the number is.
A student in a wildlife biology class wants to determine the abundance of a rodent species in a local nature preserve, divided into smaller blocks. She is concerned that she only has a modest number of traps and time to do the project, and wants to select the most appropriate sampling or experimental study design.
1. Which one of the following is most appropriate for this study?
Group of answer choices:
a. Natural experiment (observational study)
b. Stratified sampling
c. Cluster sampling
d. Systematic sampling
Answers
Answer:
c. Cluster sampling
Step-by-step explanation:
Taking into account that the exercise researcher is looking with limited resources to study a population that is divided, her best option is cluster sampling, which is a method applicable to this type of population, we could select in each group randomly her sample, the observational study is discarded because she does not have much availability of time or resources, nor would the stratified study be useful because she should select subgroups and create them to take samples and this would take more time and resources and sampling systematic is not adequate because it must have all the individuals and after having the list select the sample, but as we know, it is a process that will study the number of individuals so this option is not feasible.
Answer:
Cluster sampling
Step-by-step explanation:
Cluster sampling is almost always more economical or more practical than stratified sampling or simple random sampling as it reduces costs by increasing sampling efficiency. Due to the fact that she has limited resources, this method is better to observe clusters of units in a population than randomly selected distributed in the local nature preserve and this method is more economical and quick.
Can one of you guys pls help

Answers
Answer:
Puts the dots where the A,B,C,D dots are and move them 5 units to the right.
Example:
Original place
A=(2,5)
Moved 4 units to the right:
A'=(6,5)
Here are some tips:
Up= Y value goes up
Down= Y value goes down
Right= X value goes up
Left X value goes down
List all the subsets of the given set.
{e, n, t}
Answers
The subsets of the set {e, n, t} are given as follows:
{{}, {e}, {n}, {t}, {e,n}, {e,t}, {n,t}, {e,n,t}}.
How to obtain the number of subsets in a set?Considering a set with n elements, the number of subsets in the set is the nth power of 2, that is:
\(2^n\)
The set for this problem is given as follows:
{e, n, t}
The cardinality is given as follows:
n = 3.
Hence the number of subsets is given as follows:
2³ = 8.
The subsets are given as follows:
{{}, {e}, {n}, {t}, {e,n}, {e,t}, {n,t}, {e,n,t}}.
In which {} is the empty set.
More can be learned about the subsets of a set at brainly.com/question/13458417
#SPJ1
Solve by graphing. x2 + 2x – 3 = 0
Answers
By graphing or visualizing the parabolic shape, we can observe where the graph intersects the x-axis, which represents the solutions to the equation. In this case, the solutions are x = -3 and x = 1.
To solve the quadratic equation x^2 + 2x - 3 = 0 by graphing, we can plot the graph of the equation and find the x-values where the graph intersects the x-axis.
First, let's rearrange the equation to the standard form: x^2 + 2x - 3 = 0.
We can create a graph by plotting points for different values of x and then connecting them. However, I can describe the process and the key points on the graph.
1. Find the x-intercepts: These are the points where the graph intersects the x-axis. To find them, set y (the equation) equal to zero and solve for x:
0 = x^2 + 2x - 3.
This quadratic equation can be factored as (x + 3)(x - 1) = 0.
Therefore, x = -3 or x = 1.
2. Plot the points: Plot the points (-3, 0) and (1, 0) on the graph. These are the x-intercepts.
3. Draw the graph: The graph of the equation x^2 + 2x - 3 = 0 is a parabola that opens upward. It will pass through the x-intercepts (-3, 0) and (1, 0).
For more such questions on graph
https://brainly.com/question/19040584
#SPJ8
In a random sample of 70 undergraduate students from a large university, it was found that 37 had used library books. Find the sample proportion
Answers
Answer:
The sample proportion of undergraduate students that used library books is 0.5286.
Step-by-step explanation:
The sample proportion is the number of desired outcomes divided by the size of the sample.
In this question:
Sample of 70 undergraduate students, 37 had used library books.
\(p = \frac{37}{70} = 0.5286\)
The sample proportion of undergraduate students that used library books is 0.5286.
Determine whether the given ordered pair is a solution of the system.
(2,-1)
7x + 2y = 12
6x - 3y = 20
Answers
Answer:
Not a solution of the system
Step-by-step explanation:
Substitute 2 for x and -1 for y
\(7(2)+2(-1)=12\\6(2)-3(-1)=20\)
Simplify
\(14-2=12\\12+3=20\)
Simplify
\(12=12\\15\neq 20\)
PLEASE HELP ME!! I really need help

Answers
Answer:
(a) 1/6. One out of six sides will give you the desired result.
(b) 3/6. 3 out of 6 sides will give you the desired result.
(c) 2/3. 4 out of 6 sides will give you the desired result.
a) Multiply 82 X 34 with math workings
b) multiply 69 x 12 with math working
Answers
Multiply each term of 82 by each broken term of 34, i.e.
\( \tt \multimap \: 80 \times (30 + 4) + 2 \times (30 + 4)\)
\( \tt \nrightarrow \: 80 \times 34 + 2 \times 34\)
\( \tt \Rrightarrow \: 2720 + 68\)
\( \tt \rightharpoonup \: 2788\)
#b69 = 70-112 = 10+2Multiply each term of 69 by each broken term of 12, i.e.
\( \sf \multimap \: 70 \times (10 + 2) - 1(10 + 2)\)
\( \sf \nrightarrow \: 70 \times 12 - 1 \times 12\)
\( \sf \Rrightarrow \: 840 - 12\)
\( \sf \rightharpoondown \: 828\)
Here are the heights (in inches) of 12 students in a seminar. 71, 67, 62, 60, 70, 64, 68, 72, 58, 63, 60, 66 What is the percentage of these students who are shorter than 65 inches? 1% X 5
Answers
25% of the students in the seminar are shorter than 65 inches.
To find the percentage of students who are shorter than 65 inches, we first need to find the number of students whose height is less than 65 inches:
There are three students who are shorter than 65 inches: 62, 60, and 58.
Therefore, the percentage of students who are shorter than 65 inches is:
(3 students / 12 students) × 100% = 25%
Note that the value given for 1% × 5 does not appear to be relevant to this question, and is not necessary for the calculation of the percentage of students who are shorter than 65 inches.
For such more questions inches
https://brainly.com/question/876758
#SPJ8
Subtract the sum of 9 3/4 and 3 1/8 from 18 7/16
A. 5 9/16
B. 5 3/4
C. 6 9/16
D. 6 3/4
help pls
Answers
Answer:
A
Step-by-step explanation:
hope you have a great day!!
Find all points on the x-axis that are 14 units from the point (4, -7).
(Simplify your answer. Type an ordered pair. Use a comma to separate answers as needed.)
Answers
Answer:
The points are: (16.12,0),(-8.12,0).
Step-by-step explanation:
Solving a quadratic equation:
Given a second order polynomial expressed by the following equation:
\(ax^{2} + bx + c, a\neq0\).
This polynomial has roots \(x_{1}, x_{2}\) such that \(ax^{2} + bx + c = a(x - x_{1})*(x - x_{2})\), given by the following formulas:
\(x_{1} = \frac{-b + \sqrt{\bigtriangleup}}{2*a}\)
\(x_{2} = \frac{-b - \sqrt{\bigtriangleup}}{2*a}\)
\(\bigtriangleup = b^{2} - 4ac\)
Distance between two points:
Suppose we have two points, \((x_1,y_1)\) and \((x_2,y_2)\). The distance between them is given by:
\(D = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)
Find all points on the x-axis that are 14 units from the point (4, -7).
Being on the x-axis mean that they have y-coordinate equal to 0, so the point is (x,0).
The distance is 14. So
\(\sqrt{(x-4)^2+(0-(-7))^2} = 14\)
\(\sqrt{x^2 - 8x + 16 + 49} = 14\)
\(\sqrt{x^2 - 8x + 65} = 14\)
\((\sqrt{x^2 - 8x + 65})^2 = 14^2\)
\(x^2 - 8x + 65 - 196 = 0\)
\(x^2 - 8x - 131 = 0\)
So \(a = 1, b = -8, c = -131\)
\(\bigtriangleup = (-8)^{2} - 4(1)(-131) = 588\)
\(x_{1} = \frac{-(-8) + \sqrt{588}}{2} = 16.12\)
\(x_{1} = \frac{-(-8) - \sqrt{588}}{2} = -8.12\)
The points are: (16.12,0),(-8.12,0).
Find the solution of the system for which

Answers
Answer:
3,0,-6,0
Step-by-step explanation:
x1=3 because 3+0+0=3
since x2 and s2=0.
Solve the following inequality for zz. Write your answer in simplest form.3z - 4 > 8z + 2 ----
Answers
The expression is given as
\(3z-4\ge8z+2\)Determine the inequality,
\(-4-2\ge8z-3z\)\(-6\ge5z\)\(z\leq-\frac{6}{5}\)\(z\leq-1.2\)Hence the answer is
\(z\leq-1.2\)
A homebuyer is building a home and has sat down with an architect. The buyer tells the architect the perimeter of the house must be 200
feet. The dimensions of the house that would give the buyer the maximum area would be which of the following?
A 10 x 90 feet
B 20 x 80 feet
C 30 x 70 feet
40 x 60 feet
E 50 x 50 feet
Answers
Answer:
\(50\; {\rm ft} \times 50\; {\rm ft}\) would maximize the area for a rectangle with the given circumference of \(200\; {\rm ft}\). (Note, that a circle of the same circumference would have an even larger area.)
Step-by-step explanation:
Assume that the base of the house is a rectangle. Let the length of the two sides be \(x\; {\rm ft}\) and \(y\; {\rm ft}\), respectively. The goal is to find the \(x\) and \(y\) that:
\(\begin{aligned} \text{maximize} \quad & x\, y \\ \text{subject to} \quad & 2\, (x + y) = 200 \\ & x > 0 \\ & y > 0 \end{aligned}\).
Using the equality constraint \(2\, (x + y) = 200\) (or \(x + y = 100\)), the variable \(y\) could be replaced with \((100 - x)\) to obtain an equivalent problem of only one variable:
\(\begin{aligned} \text{maximize} \quad & x\, (100 - x) \\ \text{subject to} \quad & x > 0 \\ & (100 - x) > 0 \end{aligned}\).
Simplify to obtain:
\(\begin{aligned} \text{maximize} \quad & -x^{2} + 100\, x \\ \text{subject to} \quad & x > 0 \\ & x < 100 \end{aligned}\).
The objective function of this problem is \(f(x) = -x^{2} + 100\, x\). Derivatives of this function include
\(f^{\prime}(x) = -2\, x + 100\) and\(f^{\prime\prime}(x) = -2\).Since \(f^{\prime\prime}(x)\) is constantly less than \(0\), \(f(x)\) is concave and would be maximized when \(f^{\prime}(x) = 0\).
Setting \(f^{\prime}(x) = -2\, x + 100\) to \(0\) and solving for \(x\) gives:
\(-2\, x + 100 = 0\).
\(x = 50\).
Notice that \(x = 50\) satisfies both constraints: \(x > 0\) and \(x < 100\). Therefore, \(x = 50\) is indeed the solution that maximizes the area \(f(x) = -x^{2} + 100\, x\) while at the same time meeting the requirements.
With the length of one side being \(x = 50\) (\(50\; {\rm ft}\),) the length of the other side would be \(100 - x = 50\) (\(50\; {\rm ft}\!\).) Hence, a rectangular house of dimensions \(50\; {\rm ft} \times 50\; {\rm ft}\) would maximize the area under the given requirements.
x+11=35 solve on algebraic equation
Answers
Answer:
x = 24
Step-by-step explanation:
x + 11 = 35
x = 35 - 11
x = 24
x+11=35
Subtract 11 on both sides.
x=35−11Subtract 11 from 35 to get 24.
x=24 === AnswerVI. In a class of 40 students, the marks obtained in Mathematics (out of 50) are as under: 44,50,44,49,42,47,45,42,44,48,49,48,47 49,47,41,45,48,41,48,41,42,47,49,49,48, 50.47.49.48.46.44.45.45.46.44.42.47.48.45 ow answer the following questions: a) b) c) d) e) Find the number of students getting more than 45 marks. Find the number of students getting less than 45 marks. Find the maximum number of students getting the same marks. Find the average marks obtained by the students in the class. Find the number of students getting more than average marks.
Answers
a) To find the number of students getting more than 45 marks, we count the students whose marks are greater than 45 in the given list.
In the given list, the students with marks greater than 45 are: 50, 49, 47, 48, 49, 48, 47, 49, 48, 50, 47, 49, 48, 46, 47, 48, 47.
Counting these numbers, we find that there are 17 students who obtained more than 45 marks.
b) To find the number of students getting less than 45 marks, we count the students whose marks are less than 45 in the given list.
In the given list, the students with marks less than 45 are: 44, 44, 42, 41, 41, 42, 41, 44, 44, 42, 45, 45, 45, 44, 45.
Counting these numbers, we find that there are 15 students who obtained less than 45 marks.
c) To find the maximum number of students getting the same marks, we look for the mark that appears most frequently in the given list.
In the given list, the marks obtained by the students are: 44, 50, 44, 49, 42, 47, 45, 42, 44, 48, 49, 48, 47, 49, 47, 41, 45, 48, 41, 48, 41, 42, 47, 49, 49, 48, 50, 47, 49, 48, 46, 44, 45, 45, 46, 44, 42, 47, 48, 45.
Counting the frequency of each mark, we find that the marks 47 and 48 appear most frequently, with a count of 6 each. Therefore, the maximum number of students getting the same marks is 6.
d) To find the average marks obtained by the students in the class, we sum up all the marks and divide by the total number of students.
Total marks = 44 + 50 + 44 + 49 + 42 + 47 + 45 + 42 + 44 + 48 + 49 + 48 + 47 + 49 + 47 + 41 + 45 + 48 + 41 + 48 + 41 + 42 + 47 + 49 + 49 + 48 + 50 + 47 + 49 + 48 + 46 + 44 + 45 + 45 + 46 + 44 + 42 + 47 + 48 + 45
= 1912
Total number of students = 40
Average marks = Total marks / Total number of students
= 1912 / 40
= 47.8
Therefore, the average marks obtained by the students in the class is 47.8.
e) To find the number of students getting more than the average marks, we count the students whose marks are greater than 47.8.
In the given list, the students with marks greater than 47.8 are: 50, 50, 49, 48, 49, 48, 49, 48, 50, 49, 49, 48, 48, 50, 49, 49, 48, 48, 47, 49, 49, 48, 50, 47,
49, 49, 48, 50, 47, 49, 49, 48, 48, 49, 48, 47, 48, 49, 49, 48, 50, 49.
Counting these numbers, we find that there are 40 students who obtained more than the average marks.
Enter the number that belongs in the green box

Answers
The angle measure that belongs in the green box is given as follows:
70.67º.
What is the law of sines?We consider a triangle with side lengths and angles related as follows, as is the case for this problem:
Side length of a is opposite to angle A.Side length of b is opposite to angle B.Side length of c is opposite to angle C.Then the lengths and the sines of the angles are related as follows:
sin(A)/a = sin(B)/b = sin(C)/c.
The relation for this problem is given as follows:
sin(x)/12 = sin(76º)/12.34
Applying cross multiplication, the missing angle measure is given as follows:
sin(x) = 12 x sine of 76 degrees/12.34
sin(x) = 0.9436.
x = arcsin(0.9436)
x = 70.67º.
More can be learned about the law of sines at https://brainly.com/question/4372174
#SPJ1
Ms.Chase expected to get $520 for her birthday, but she only got $355. What was the percentage error? (Round to the nearest whole number)
Answers
Answer:
46
Step-by-step explanation:
520-355 = 165
165/355 = 0.46
0.46 x 100 = 46
Which is the graph of y = cos(x – 9)?

Answers
Answer:
The function y=cos(x-π) is the left graph
Step-by-step explanation:
y=cos(x-π) represents a horizontal shift to the right by π units from the parent function y=cos(x). Since y=cos(x) starts at the maximum, then shifting the function to the right by π units gives the leftmost graph.
Solve using the quadratic formula. 9q2 + 6q + 1 = 0 Write your answers as integers, proper or improper fractions in simplest form, or decimals rounded to the nearest hundredth. q = or q =
Answers
The solution to the quadratic equation is given as follows: \(q = -\frac{1}{3}\)
What is a quadratic function?A quadratic function is given according to the following rule:
\(y = ax^2 + bx + c\)
The solutions are:
\(x_1 = \frac{-b + \sqrt{\Delta}}{2a}\)\(x_2 = \frac{-b - \sqrt{\Delta}}{2a}\)In which:
\(\Delta = b^2 - 4ac\)
In this problem, the equation is:
9q² + 6q + 1.
The coefficients are a = 9,b = 6, c = 1, hence:
\(\Delta = 6^2 - 4(9)(1) = 0\)
\(q_1 = \frac{-6 + \sqrt{0}}{2(9)} = -\frac{1}{3}\)
\(q_2 = \frac{-6 - \sqrt{0}}{2(9)} = -\frac{1}{3}\)
More can be learned about quadratic functions at https://brainly.com/question/24737967
#SPJ1
The point (4,5) is translated two units left and eight units down. What is the y-coordinate of the image?
Answers
Answer:
-3
Step-by-step explanation:
Answer:
-3
Have fun!!
Step-by-step explanation:
Find the surface area of the prism.
mi
8 mi
8/12 mi
The surface area is
square miles.
112

Answers
Answer: 433.5 square miles or 433 1/2 square miles
Step-by-step explanation
\(SA = 6x^{2}\)
\(SA = 6 *(8.5)^{2} \\\\SA = 6*72.25\\\\SA = 433.5\)
answer the questions below to find the total surface area of the can

Answers
The total surface area of the tomato ketchup given in the diagram can be determined as follows:
The total surface area of a shape is the addition of the areas of its individual surface.
So that the questions can be answered as thus:
A. To find the area of the given circle;
i. Area of a circle = \(\pi r^{2}\)
where r is the radius of the circle.
area of the circle = π\((2.5)^{2}\)
= 6.25\(\pi\)
ii. There are two identical circles in the cylinder.
iii. The total area of all circles = 2(6.25\(\pi\))
= 12.5\(\pi\) square inches
B. To find the area of the rectangle;
i. one side of the rectangle is 5 inches.
ii. The other side of the rectangle = 2\(\pi\)r
= 2(2.5)\(\pi\)
= 5\(\pi\) inches
iii. The area of the rectangle = l x b
= 5\(\pi\) x 5
= 25\(\pi\) square inches
C. Total surfce area of the cylinder = 5\(\pi\) + 25\(\pi\)
= 30\(\pi\) square inches
For more clarifications on total surface area of a cylinder, check: https://brainly.com/question/16990329
#SPJ1
Answer:
Step-by-step explanation:
First box
6.25
2
12.5
------
Second box
------
5
5
25
------
Last box
------
37.5
36.
A meeting started at 11.35a.m. and
ended at 4.15p.m the same day. How
long did the meeting last?
a) 3hrs 40mins
b) 3hrs 50mins
c) 4hrs 35mins
d) 4hrs 40mins
e) 5hrs 40mins
What’s the answer
Answers
Answer:
Step-by-step explanation:
option (d) 4hrs 40mins
