Answers
Answer:
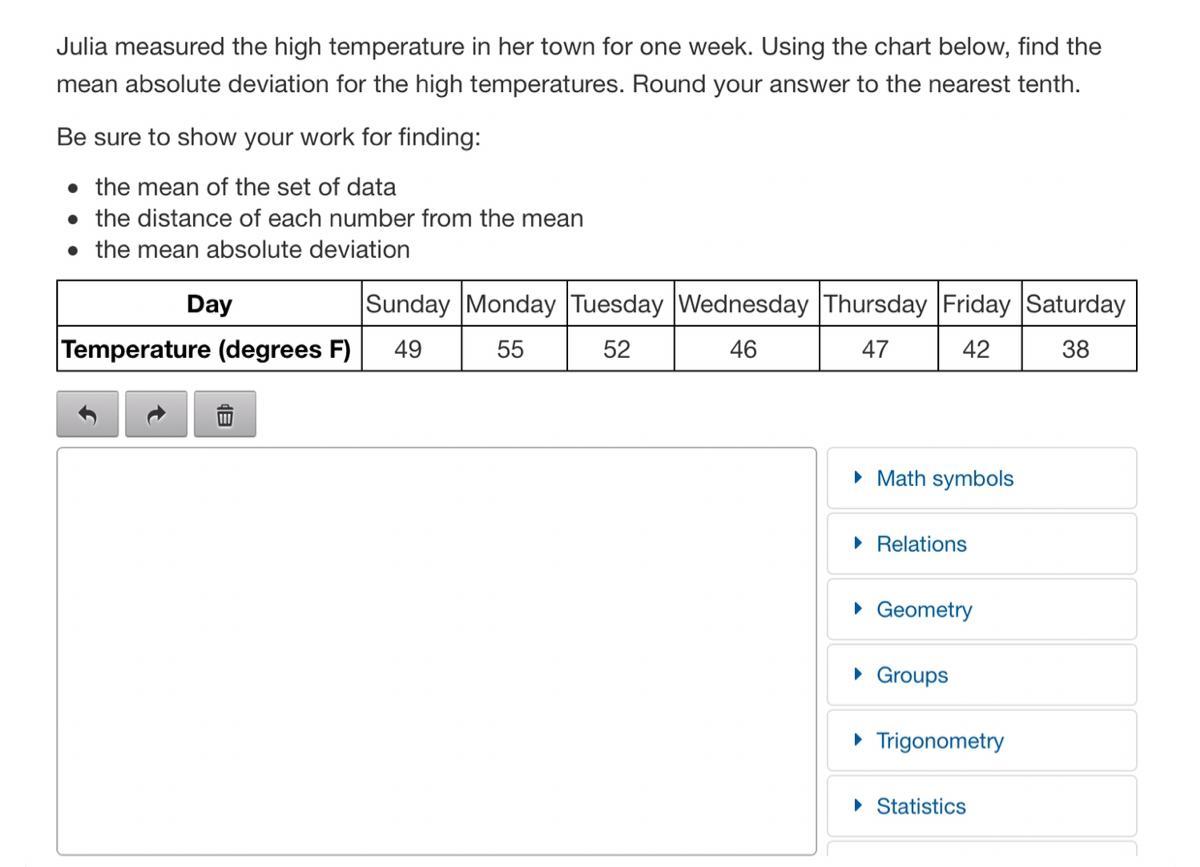
Sunday: 50 Monday: 60 Tuesday: 50 Wednesday: 50 Friday: 40 Saturday: 40
Step-by-step explanation:
That's If Its To The Nearest Tenth If This Is What U Wanted I'm Just Doing What The Instructions Told Me
Related Questions
For the function f(x) = x^1/3/3 find f^-1(x)

Answers
Answer:
To get f⁻¹(x), write f(x) = y = x^(1/3)/3, exchange x and y, so x = y^(1/3)/3, then y = (3x)³, this is just the f⁻¹(x) = (3x)³.
Step-by-step explanation:
Question 2 The current report quantitatively analyzes three variables - load factors, revenue passenger mile, and available seat miles for American Airlines. The data retrieved for the analysis was extracted from the Bureau of Transportation Statistics, focusing on domestic flights from January 2006 to December 2012. The quantitative analysis focused on finding critical statistical values like mean, median, mode, standard deviation, variance, and minimum/maximum variables. Table 2: Summary Statistics of American Airlines (Domestic) Revenue Passenger Miles Mean 6,624,897 Median 6,522,230 Mode NONE Minimum 5,208,159 Maximum 8,277,155 Standard Dev 720,158.571 Variance 518,628,367,282.42 Load Factors Mean 82.934 Median 83.355 Mode 84.56 Minimum 74.91 Maximum 89.94 Standard Dev 3.972 Variance 15.762 Revenue Passenger Miles 9000000 8000000 7000000 6000000 5000000 4000000 3000000 2000000 1000000 0 0 10 American Airlines (Domestic) Performance 20 30 ● Revenue Passenger Miles 40 50 Load Factors Available Seat Miles 60 Mean 7,984,735 Median 7,753,372 Mode NONE Minimum 6,734,620 Maximum 9,424,489 Standard Dev 744,469.8849 Variance 554,235,409,510.06 70 80 Linear (Revenue Passenger Miles) 90 100 Figure 1: American Airlines (Domestic) Performance Write a report based on the given data. Please include additional tests such as hypothesis testing, skewness, z statistic, level of significance, and other necessary tests, as well as a discussion of the results obtained.
Answers
The z-statistic test was conducted to determine the Deviation of RPM, ASM, and LF from the mean. The test indicates that RPM, ASM, and LF significantly deviate from the mean.
Report on the Analysis of American Airlines (Domestic) PerformanceThe quantitative analysis focused on three variables- load factors, revenue passenger miles, and available seat miles for American Airlines.
The Bureau of Transportation Statistics data for domestic flights from January 2006 to December 2012 was retrieved for the analysis. The quantitative analysis also focused on finding critical statistical values like mean, median, mode, standard deviation, variance, and minimum/maximum variables. The results of the data are summarized in Table 2. Revenue Passenger Miles (RPM) mean is 6,624,897, the median is 6,522,230, and mode is NONE. The minimum is 5,208,159 and the maximum is 8,277,155. The standard deviation is 720,158.571, and the variance is 518,628,367,282.42.
Load Factors (LF) mean is 82.934, the median is 83.355, and mode is 84.56. The minimum is 74.91, and the maximum is 89.94. The standard deviation is 3.972, and the variance is 15.762. The Available Seat Miles (ASM) mean is 7,984,735, the median is 7,753,372, and mode is NONE. The minimum is 6,734,620, and the maximum is 9,424,489. The standard deviation is 744,469.8849, and the variance is 554,235,409,510.06.Figure 1 above displays the performance of American Airlines (Domestic).
The mean RPM is 7,984,735, and the linear regression line is y = 50584x - 2.53E+8. The linear regression line indicates a positive relationship between RPM and year, with a coefficient of determination, R² = 0.6806. A coefficient of determination indicates the proportion of the variance in the dependent variable that is predictable from the independent variable. Therefore, 68.06% of the variance in RPM is predictable from the year. A one-way ANOVA analysis of variance test was conducted to determine the equality of means of three groups of variables; RPM, ASM, and LF. The null hypothesis is that the means of RPM, ASM, and LF are equal.
The alternative hypothesis is that the means of RPM, ASM, and LF are not equal. The level of significance is 0.05. The ANOVA results indicate that there is a significant difference in means of RPM, ASM, and LF (F = 17335.276, p < 0.05). Furthermore, a post-hoc Tukey's test was conducted to determine which variable means differ significantly. The test indicates that RPM, ASM, and LF means differ significantly.
The skewness test was conducted to determine the symmetry of the distribution of RPM, ASM, and LF. The test indicates that the distribution of RPM, ASM, and LF is not symmetrical (Skewness > 0).
Additionally, the z-statistic test was conducted to determine the deviation of RPM, ASM, and LF from the mean. The test indicates that RPM, ASM, and LF significantly deviate from the mean.
For more questions on Deviation .
https://brainly.com/question/24298037
#SPJ8
can somebody help me with this iready problem because I just need 60 minutes and I don't wanna mess this up

Answers
Answer:
the answer is 2\(\frac{1}{4}\)
Step-by-step explanation:
(3/4) + (3/4) + (3/4) = 2.25 --> \(2\frac{1}{4}\)
The radius r of a sphere is increasing at a rate of 3 inches per minute. (a) Find the rate of change of the volume when r = 9 inches. in.3/min (b) Find the rate of change of the volume when r = 37 inches. in.3/min
Answers
Answer:
\(\frac{dV}{dt}\) = 1017.87 in³/min
\(\frac{dV}{dt}\) = 17203.35 in³/min
Step-by-step explanation:
given data
radius r of a sphere is increasing at a rate = 3 inches per minute
\(\frac{dr}{dt}\) = 3
solution
we know volume of sphere is V = \(\frac{4}{3} \pi r^3\)
so \(\frac{dV}{dt} = \frac{4}{3} \pi r^2 \frac{dr}{dt}\)
and when r = 9
so rate of change of the volume will be
rate of change of the volume \(\frac{dV}{dt} = \frac{4}{3} \pi (9)^2 (3)\)
\(\frac{dV}{dt}\) = 1017.87 in³/min
and
when r = 37 inches
so rate of change of the volume will be
rate of change of the volume \(\frac{dV}{dt} = \frac{4}{3} \pi (37)^2 (3)\)
\(\frac{dV}{dt}\) = 17203.35 in³/min
Find value of x in trapezoid

Answers
Answer:
x = 1
Step-by-step explanation:
You want to know the value of x in the trapezoid with adjacent angles (43x+2)° and 135°.
Supplementary anglesThe two marked angles can be considered "consecutive interior angles" where a transversal crosses parallel lines. As such, they are supplementary.
(43x +2)° +135° = 180°
43x = 43 . . . . . . . . . . . . . . divide by °, subtract 137
x = 1 . . . . . . . . . . . . . . . divide by 43
The value of x is 1.
__
Additional comment
Given that the figure is a trapezoid, we have to assume that the top and bottom horizontal lines are the parallel bases.
<95141404393>
A number rounds down to 600 to 1 significant figure. What could the original number
be?
Answers
Answer:
1000
Step-by-step explanation:
Round the 6 in 600, this is 1 significant figure.6 rounds up to 10 making 1000
The number can be 601, 602, 603, ....... 699
What is significant figures?Significant figures are the number of digits in a value, often a measurement, that contribute to the degree of accuracy of the value. We start counting significant figures at the first non-zero digit.
If the number is round down to 600 then it's depend on round off
If the round off should be at hundred place, then number can be
601,602, ..................649.
If we round off the above number then it will be 600 which has 1 significant figure.
Learn more about significant figure here:
https://brainly.com/question/14359464
#SPJ2
what is the average rate of change for this quadratic function fo rate interval from x=-4 to x=-2
Answers
Answer:
ill edit my comment later but is there a graph? its not enough info
Step-by-step explanation:
not enough info i think
I keep getting the wrong answer.

Answers
The volume of the solid obtained by rotating the region bounded by the curve y = 1 - (x - 5)² in the first quadrant about the y-axis is 51π cubic units.
What is the volume of the solid obtained by rotating the region in the first quadrant bounded by the given curve about the y - axis?To find the volume of the solid obtained by rotating the region bounded by the curve y = 1 - (x - 5)² in the first quadrant about the y-axis, we can use the method of cylindrical shells.
The formula for the volume using cylindrical shells is:
V = 2π ∫ [a, b] x * h(x) dx
Where:
- V is the volume of the solid
- π represents the mathematical constant pi
- [a, b] is the interval over which we are integrating
- x is the variable representing the x-axis
- h(x) is the height of the cylindrical shell at a given x-value
In this case, we need to solve for x in terms of y to express the equation in terms of y.
Rearranging the given equation:
x = 5 ± √(1 - y)
Since we are only interested in the region in the first quadrant, we take the positive square root:
x = 5 + √(1 - y)
Now we can rewrite the volume formula with respect to y:
V = 2π ∫ [c, d] x * h(y) dy
Where:
- [c, d] is the interval of y-values that correspond to the region in the first quadrant
To determine the interval [c, d], we set the equation equal to zero and solve for y:
1 - (x - 5)² = 0
Expanding and rearranging the equation:
(x - 5)² = 1
x - 5 = ±√1
x = 5 ± 1
Since we are only interested in the region in the first quadrant, we take the value x = 6:
x = 6
Now we can evaluate the integral to find the volume:
V = 2π ∫ [0, 1] x * h(y) dy
Where h(y) represents the height of the cylindrical shell at a given y-value.
Integrating the expression:
V = 2π ∫ [0, 1] (5 + √(1 - y)) * h(y) dy
To find h(y), we need to determine the distance between the y-axis and the curve at a given y-value. Since the curve is symmetric, h(y) is simply the x-coordinate at that point:
h(y) = 5 + √(1 - y)
Substituting this expression back into the integral:
V = 2π ∫ [0, 1] (5 + √(1 - y)) * (5 + √(1 - y)) dy
Now, we can evaluate this integral to find the volume
V = 2π ∫ [0, 1] (5 + √(1 - y)) * (5 + √(1 - y)) dy
To simplify the integral, let's expand the expression:
V = 2π ∫ [0, 1] (25 + 10√(1 - y) + 1 - y) dy
V = 2π ∫ [0, 1] (26 + 10√(1 - y) - y) dy
Now, let's integrate term by term:
\(V = 2\pi [26y + 10/3 * (1 - y)^\frac{3}{2} - 1/2 * y^2]\)] evaluated from 0 to 1
V = \(2\pi [(26 + 10/3 * (1 - 1)^\frac{3}{2} - 1/2 * 1^2) - (26 * 0 + 10/3 * (1 - 0)^\frac{3}{2} - 1/2 * 0^2)]\)
V = 2π [(26 + 0 - 1/2) - (0 + 10/3 - 0)]
V = 2π (25.5)
V = 51π cubic units
Learn more on volume of a solid obtained by rotating curve here;
https://brainly.com/question/32301706
#SPJ1
Every 2 centimeters on a floor plan represents
meters of the house. The dining room is 8 cm by
10 cm on the floor plan, and the bedroom is 6cm by10cm on the floor plan. If installing tile costs $34
per square meter and installing carpet costs $21 per
square meter, how much would it cost to install tile
in the dining room and install carpet in the bedroom?
Show your work.
Answers
Given statement solution is :- It would cost $680 to install tile in the dining room and $315 to install carpet in the bedroom.
To find the cost of installing tile in the dining room and carpet in the bedroom, we need to calculate the areas of both rooms first.
Given:
Every 2 centimeters on the floor plan represents 1 meter of the house.
Dining Room:
On the floor plan, the dining room is 8 cm by 10 cm.
Converting this to meters, the dimensions of the dining room are 8 cm / 2 = 4 meters by 10 cm / 2 = 5 meters.
The area of the dining room is 4 meters * 5 meters = 20 square meters.
Bedroom:
On the floor plan, the bedroom is 6 cm by 10 cm.
Converting this to meters, the dimensions of the bedroom are 6 cm / 2 = 3 meters by 10 cm / 2 = 5 meters.
The area of the bedroom is 3 meters * 5 meters = 15 square meters.
Now, let's calculate the costs.
Cost of Tile:
The cost of installing tile is $34 per square meter.
The area of the dining room is 20 square meters.
Therefore, the cost of installing tile in the dining room is 20 square meters * $34/square meter = $680.
Cost of Carpet:
The cost of installing carpet is $21 per square meter.
The area of the bedroom is 15 square meters.
Therefore, the cost of installing carpet in the bedroom is 15 square meters * $21/square meter = $315.
Therefore, it would cost $680 to install tile in the dining room and $315 to install carpet in the bedroom.
For such more questions on Cost of tile and carpet.
https://brainly.com/question/29574063
#SPJ8
A mathematical model is a simplified description of a system or a process. In your opinion, how are mathematical models helpful? What are the advantages and disadvantages of using a model? In what ways are mathematical models linked to the fields of chemistry, biology, and physics? Cite several examples.
Answers
Given statement solution is :- Mathematical models are extremely valuable tools in various fields, including chemistry, biology, and physics. They offer several advantages: Simplification and abstraction, Prediction and simulation, Cost and time efficiency, Insight and understanding.
Mathematical models are extremely valuable tools in various fields, including chemistry, biology, and physics. They offer several advantages:
Simplification and abstraction: Mathematical models allow complex systems or processes to be represented using simplified mathematical equations or algorithms. This simplification helps in understanding the underlying principles and relationships of the system, making it easier to analyze and predict outcomes.
Prediction and simulation: Models enable scientists to make predictions about the behavior of a system under different conditions. They can simulate scenarios that are difficult or impossible to observe in the real world, allowing researchers to explore various hypotheses and make informed decisions.
Cost and time efficiency: Models can be used to explore different scenarios and test hypotheses in a relatively quick and cost-effective manner compared to conducting real-world experiments. They can help guide experimental design by providing insights into the most relevant variables and parameters.
Insight and understanding: Mathematical models often reveal underlying patterns and relationships that may not be immediately apparent from experimental data alone. They provide a framework for organizing and interpreting data, leading to a deeper understanding of the system being studied.
However, mathematical models also have limitations and potential disadvantages:
Simplifying assumptions: Models are based on assumptions and simplifications, which may not fully capture the complexity of the real-world system. If these assumptions are incorrect or oversimplified, the model's predictions may be inaccurate or misleading.
Uncertainty and error: Models are subject to uncertainties and errors stemming from the inherent variability of the system, limitations in data availability or quality, and simplifying assumptions. It is crucial to assess and communicate the uncertainties associated with model predictions.
Validation and verification: Models need to be validated and verified against experimental data to ensure their accuracy and reliability. This process requires rigorous testing and comparison to real-world observations, which can be challenging and time-consuming.
Mathematical models are closely linked to the fields of chemistry, biology, and physics, providing valuable insights and predictions in these disciplines. Here are some examples:
Chemistry: Mathematical models are used to study chemical reactions, reaction kinetics, and molecular dynamics. One example is the use of rate equations to model the kinetics of a chemical reaction, such as the reaction between reactants A and B to form product C.
Biology: Mathematical models play a crucial role in understanding biological systems, such as population dynamics, gene regulation, and the spread of infectious diseases. For instance, epidemiological models like the SIR (Susceptible-Infectious-Recovered) model are used to simulate and predict the spread of diseases within a population.
Physics: Mathematical models are fundamental in physics to describe physical phenomena and predict outcomes. One well-known example is Newton's laws of motion, which can be mathematically modeled to predict the motion of objects under the influence of forces.
Quantum mechanics: Mathematical models, such as Schrödinger's equation, are used to describe the behavior of particles at the quantum level, providing insights into atomic and molecular structures and the behavior of subatomic particles.
Fluid dynamics: Mathematical models, such as the Navier-Stokes equations, are employed to study the behavior of fluids, including airflow, water flow, and weather patterns.
These examples demonstrate the wide range of applications for mathematical models in understanding, predicting, and simulating various phenomena in the fields of chemistry, biology, and physics.
For such more questions on Advantages of Mathematical Models
https://brainly.com/question/12653211
#SPJ8
Solve the inequality. Graph the solution.Z/4 is less than or equal to 12.
Answers
You have the following inequality:
z/4 ≤ 12
To solve the previous inequality you proceed as follow:
z/4 ≤ 12 multiply both sides by 4
z ≤ 48
Hence, the solution is z ≤ 48
when you want to graph a solution of the form "z lower or equal than", you draw a black point, that means the solution are all number lower than 48, including 48.

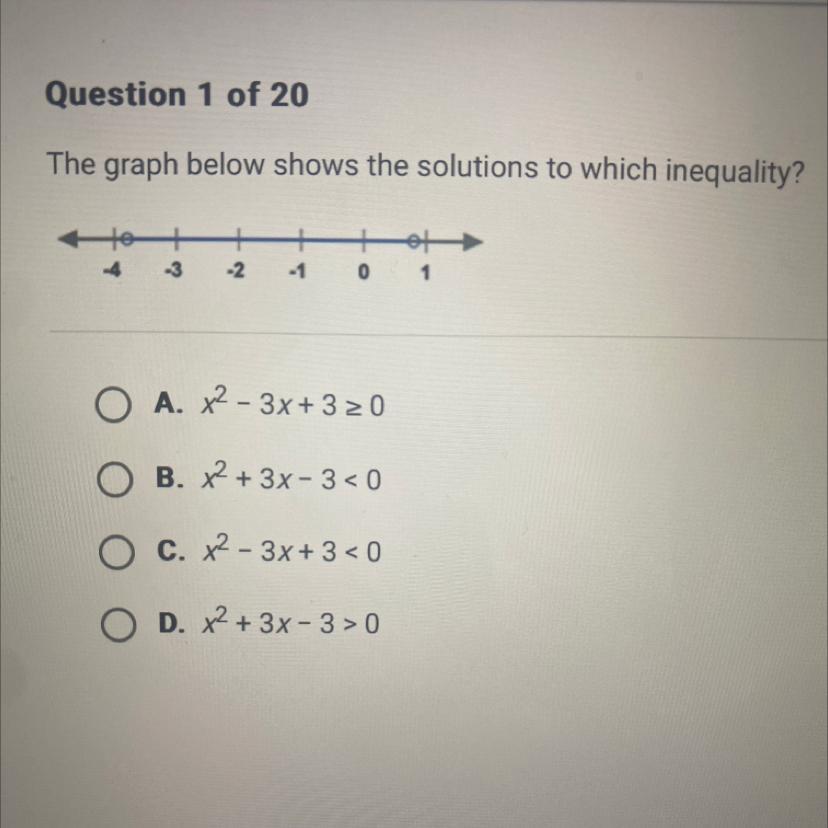
The graph below shows the solutions to which inequality?
A. x^2-3x+3 ≥0
B. x² + 3x-3 <0
C. x²-3x+3<0
D. x² + 3x-3>0
Answers
The inequality expression that corresponds to the solution of the inequality graph is x² + 3x - 3 < 0.
option B.
What is the solution of the inequality?The inequality expression that corresponds to the solution of the inequality graph is determined by simplifying the equations as follows;
The solution of the graph,
x > -4 and x < 1
The first equation with "≥" is ruled out because the graph doesn't have a thick dot.
Let's simplify the second expression;
x² + 3x - 3 < 0
solve using quadratic formula;
x > -3.79 or x < 0.79
The third expression is ruled out since its solution will be complex.
For the last expression;
x² + 3x - 3 > 0
x < -3.79 or x > 0.79
Thus, the correct inequality expression is x² + 3x - 3 < 0.
Learn more about inequality expression here: https://brainly.com/question/25275758
#SPJ1
the table below shows some inputs and outputs of the invertible function f etc

Answers
Answer:
\((a)\ f^{-1}(-15) = -6\)
\((b)\ f^{-1}(4) + f(9)=0\)
Step-by-step explanation:
Given
The attached table
\((a)\ f^{-1}(-15)\)
This represents an inverse function.
So, we look into x row for its value.
i.e.
\(f^{-1}(-15) = -6\)
\((b)\ f^{-1}(4) + f(9)\)
Just like (a)
\(f^{-1}(4) = -11\) ---- by looking into the x rows
\(f(9) = 11\)
So:
\(f^{-1}(4) + f(9)=-11 + 11\)
\(f^{-1}(4) + f(9)=0\)
Find the slope of the graphed line

Answers
Answer:
5/3
Step-by-step explanation:
use the rise/run tactic
20/48 equals what as a percentage
Answers
Answer:
approx 41.6%
Step-by-step explanation:
Answer:
41.7%
Step-by-step explanation:
First, you will divide 20 by 48.
\(20/48=0.4167\)
Secondly, you would multiply by 100%
\(0.4167* 100= 41.67%\)%
If you round to the nearest whole number it would give you \(42\)%. If it is rounded to the nearest tenth it would be \(41.7%\)%
question is in the picture, thank you so much in advance.

Answers
Answer:
y¹⁰
Step-by-step explanation:
Let’s say y=2.
This means 2 to the power of 4 is 16.
Then, we do 16 times 2, because it says y4 times 6.
16 times 2 is 32.
Now we find what 2 to the power of 5 is.
That is also 32.
Finally, we do 32 times 32 which is 1,024.
As you can see, we used 2, aka y 10 times. This is because y4 has 4 y’s, and y5 has 5 y’s. Then, there is one extra y in the middle.
Therefore, 4 + 5 + 1 is equal to 10.
This can be written as y10.
hope this helped!
Find m and c for this line
Y+3x=1
Answers
Answer:
m = -3 ; c = 1
Step-by-step explanation:
y = -3x + 1
y = mx + c
m = -3
c = 1
Graph the system of equations on your graph paper to answer the question.
{y=x−4y=−x+6
What is the solution for this system of equations?
Answers
Answer: (5 , 1)
Step-by-Step explanation:
hihi your problem is a system of question y = x-4 and y = -x+6 okay so graph them both normally and then find the point where they intersect which is gonna be a coordinate point, and that's your solution !!
y = x-4
the y intersect is going to be 4
the slope is a positive 1 , going up to the right, through the positive quadrant, line is facing to the right
y = -x+6
the y intersect is going to be -6
the slope is going to be a -1 , following up the opposite way the line is going to face the left
once you graph them both you'll see the point of intersection, the solution
make sure you drew your lines very clearly !!!!
the solution is x = 5 and y = 1 which is also (5 , 1)
hopefully this was helpful !
d = √(x2 - x1)2 + (y2 - y1)2, what is the distance between point (3, 2) and point (5, 4) rounded to nearest 10th
Answers
What is one plus sixety-four
Answers
Answer:
65
Step-by-step explanation:
Answer:
like 149
Step-by-step explanation:
big brain
Select the interval(s) where the function is increasing:
f(x) = x ^ 4 - 5x ^ 2 - 3
(- 9.3, - 3)
(- ∞,- 1.5)
(0, 1.5)
(-1.5, 0)
(1.5, ∞)
(-∞, ∞)
(-9.3, ∞)
Answers
(-1.5, 0) and (1.5, ∞)
Solve the given initial-value problem.
d2x/dt2 + 4x = −2 sin(2t) + 8 cos(2t),
x(0) = −1, x'(0) = 1
Answers
Combining the homogeneous and the particular solutions, and applying the initial conditions, the solution to the given IVP is:
\(x(t) = -\cos{(2t)} + \frac{1}{2}\sin{(2t)}\)
The IVP is given by:
\(x^{\prime\prime} + 4x = -2\sin{(2t)} + 8\cos{(2t)}\)
First, we find the homogeneous solution, which depends on the roots of the characteristic equation, given by:
\(r^2 + 4 = 0\)
\(r^2 = -4\)
\(r = \pm \sqrt{-4}\)
\(r = \pm 2i\)
Thus:
\(x_h(t) = a\cos{(2t)} + b\sin{(2t)}\)
Then, according to the source(left-side of the equality), the particular solution has the following format:
\(x_p(t) = A\cos{(2t)} + B\sin{(2t)}\)
Applying the derivatives:
\(x_p^{\prime}(t) = -2A\sin{(2t)} + 2B\cos{(2t)}\)
\(x_p^{\prime\prime}(t) = -4A\cos{(2t)} - 4B\sin{(2t)}\)
Replacing into the IVP:
\(x^{\prime\prime} + 4x = -2\sin{(2t)} + 8\cos{(2t)}\)
\(-4A\cos{(2t)} - 4B\sin{(2t)} + 4A\cos{(2t)} + 4B\sin{(2t)} = -2\sin{(2t)} + 8\cos{(2t)}\)
\(0A\cos{(2t)} + 0B\sin{(2t)} = -2\sin{(2t)} + 8\cos{(2t)}\)
Thus, the particular solution is \(x_p(t) = 0\).
The complete solution is:
\(x(t) = x_h(t) + x_p(t)\)
\(x(t) = x_h(t)\)
\(x(t) = A\cos{(2t)} + B\sin{(2t)}\)
Applying the initial conditions:
\(x(0) = -1 \rightarrow A + 0B = -1 \rightarrow A = -1\)
\(x^{\prime}(0) = 1 \rightarrow 2B = 1 \rightarrow B = \frac{1}{2}\)
Thus, the solution is:
\(x(t) = -\cos{(2t)} + \frac{1}{2}\sin{(2t)}\)
A similar problem is given at https://brainly.com/question/13143214
The table below shows the probability distribution of a random variable Z.
Z P(Z)
4 0
5 0.1
6 0.7
7 0.2
What is the variance of Z?
Write your answer as a decimal. Do not round.
Answers
The variance of Z is 1.67
What is a variance?
A data set's variance is a measure of dispersion that accounts for the spread of each data point. Along with the standard deviation, which is just the square root of the variance, it is the measure of dispersion that is most frequently employed.
To calculate the variance,
First, we need to calculate the mean.
So, the Mean of Z = \(\frac{4+5+6+7}{4}\) = 5.5
Then,
the variance of Z = \(\frac{(4-5.5)^{2} + (5-5.5)^{2}+(6-5.5)^{2}+(7-5.5)^{2} }{3}\) = 1.67
Hence, the variance of Z is 1.67
To learn more about variance
https://brainly.com/question/9304306
#SPJ1
Could someone help solve question 50? (One on left) thanks!!

Answers
First we are going to use the sin trigonometric function to find x,
\(\sin 45\text{ = }\frac{12\text{ cm}}{x}\Rightarrow\text{ x= }\frac{12\text{ cm}}{\sin 45}=\text{ }\frac{12\text{ cm}}{\frac{\sqrt[]{2}}{2}}=\frac{24}{\sqrt[]{2}}cm=\text{ 12}\sqrt[]{2}\text{ cm}\)Now, we do the analogous procedure for the angle of 30 degrees
\(\begin{gathered} \sin 30=\text{ }\frac{x}{z}\text{ }\Rightarrow\text{ z=}\frac{x\text{ }}{\sin 30}=\frac{12\sqrt[]{2}\text{ cm}}{\frac{1}{2}}=\text{ 24}\sqrt[]{2\text{ }}cm \\ \tan 30=\text{ }\frac{x}{y}\text{ }\Rightarrow\text{ y= }\frac{x}{\text{tan}30}=\frac{12\sqrt[]{2}cm}{\frac{\sqrt[]{3}}{3}}=\text{ 12}\sqrt[]{2}\sqrt[]{3}\text{ cm =12}\sqrt[]{6}\text{ cm} \end{gathered}\)I need an idea for how to film something maybe around 30 seconds using this criteria. I can use anything in my house and have one actor.
EXERCISE
Use framing to shoot a scene that creates a feeling of a character being trapped (claustrophobia), then emerging from that sense of entrapment.
● Use six shots
● Do not use camera movement
● Do not rely on acting
Answers
Answer: you can maybe show them being trapped in the bathroom them come in with a sharp knife and splash or put ketchup on the part you stabbbed them
Step-by-step explanation:
Type < or > to make this statement true -a___-b
Answers
The comparisons that are true are 11. -5 < 0 12. 9 > -8 14. 55 > -75 15. -32 < -24 16. 89 > 73 17. -58 < -51 19. 17 < 23 20. 18 > -36 and that is not true are 13. -7 = -7 (not true) 18. -32 > 4 (not true)
To make each statement true, write < or >. We need to compare two values for each statement to determine whether it is true or false.
To indicate that the first value is less than the second value, write <.
Alternatively, to indicate that the first value is greater than the second value, write >.
Below are the comparisons: 11. -5 < 0 12. 9 > -8 13. -7 > -7 14. 55 > -75 15. -32 < -24 16. 89 > 73 17. -58 < -51 18. -32 > 4 19. 17 > 23 20. 18 > -36
To determine the direction of inequality, we need to compare the values.
We used inequality signs such as > (greater than) or < (less than) to indicate which value is larger or smaller than the other.
For more questions on comparisons
https://brainly.com/question/30097421
#SPJ8
The correct question would be as
Write > or < to make each statement true.
11. -5 0
12. 9 -8
13. -7 7
14. 55 -75
15. -32 -24
16. 89 73
17. -58 -51
18. -32 4
19. 17 23
20. 18 -36
There is a straight road between town A and town B of length 130 km.
Maxi travels from town A to town B.
Pippa travels from town B to town A.
Both travel at a constant speed of 40 km/h.
Maxi leaves 30 minutes before Pippa.
Work out how far from town A they will be when they pass each other
Answers
They will be when they pass each other at 44 4/9 mins.
This is a classic question on Speed, time, & distance.
1. When time traveled in each segment is constant, then average speed is simple mean of speeds.
2. When distance traveled in each segment is constant, then average speed is reciprocal of simple mean of reciprocal of speeds. It is basically called Harmonic mean.
So this question falls in the category of 2.
=> So, average speed = Reciprocal of mean of reciprocals of 40 & 50.
=> Average speed = Reciprocal of mean of 1/40 & 1/50.
=> Average speed = Reciprocal of (1/40 + 1/50)/2
= Reciprocal of (5+4)/400
= 44 4/9 mins
Hence, they will be when they pass each other at 44 4/9 mins.
To know more about speed check the below link:
https://brainly.com/question/4931057
#SPJ1
(Solving for a). b=(4*a)-3/4
Answers
Answer:
a = 3/28
Step-by-step explanation:
To start solving for a variable, you need to isolate it.
-4/3b = 4a
-4/3 divided by 4 equals -4/12 or -1/3
a = -1/3b
To completely solve for a we need to plug it back in and solve for b.
b = (4(-1/3b)) - 3/4
b = -4/3b - 3/4
7/3b = -3/4
b = -9/28
Finally, we can plug b back in to the previous equation we got for a to solve for a.
a = -1/3(-9/28)
a = 3/28
Furthermore, we can check if this is correct by plugging in 3/28 for a into the original problem and see if we get what we got for b (-9/28)
What was the percent increase of China's
population from 1970 to 1995?
56.25%
45%
156.25%
9.405%
China's Population
Population
(billions)
0.7
Year
1965
1970
1975
1980
1985
1990
1995
2000
0.8
0.92
0.98
1.08
1.14
1.25
1.26
Answers
The percentage increase China's population from 1970 to 1995 is: 56.25%.
How to Calculate Percentage Increase?Percentage increase = (Final Value - Original Value)/Original value × 100.
Given the following:
Original value = 0.8 billion
Final Value = 1.25 billion
Final Value - Original Value = 1.25 - 0.8
Final Value - Original Value = 0.45
Percentage increase = 0.45/0.8 × 100 = 56.25%.
Learn more about percentage increase on:
https://brainly.com/question/14129404
#SPJ1
at.the zoo there is a ratio of zebra to giraffes 5:2 there are 21 animals how many zebra and how many graffies
Answers
Step-by-step explanation:
Given that the ratio of zebras are 5 and giraffes are 2
We add them giving is 7
So: giraffe=2/7 × 21 = 6
Zebra 5/7 × 21 = 15