three bolts and three nuts are in a box. two parts are chosen at random. find the probability that one is a bolt and one is a nut.
Answers
The probability of picking one bolt and one nut is 1/2 or 50%.
To find the probability that one is a bolt and one is a nut, we need to use the formula for calculating the probability of two independent events happening together: P(A and B) = P(A) × P(B)
Let's first calculate the probability of picking a bolt from the box:
P(bolt) = number of bolts / total number of parts = 3/6 = 1/2
Now, let's calculate the probability of picking a nut from the box:
P(nut) = number of nuts / total number of parts = 3/6 = 1/2
Since the events are independent, the probability of picking a bolt and a nut in any order is:
P(bolt and nut) = P(bolt) × P(nut) + P(nut) × P(bolt)
P(bolt and nut) = (1/2) × (1/2) + (1/2) × (1/2)
P(bolt and nut) = 1/2
Therefore, the probability of picking one bolt and one nut is 1/2 or 50%.
Learn more about probability
https://brainly.com/question/30034780
#SPJ4
the probability that one chosen part is a bolt and the other chosen part is a nut is 1, or 100%. This makes sense because if we choose two parts at random, we must get one bolt and one nut since there are three of each in the box.
To find the probability that one chosen part is a bolt and the other chosen part is a nut, we need to use the formula for probability:
Probability = (number of desired outcomes) / (total number of outcomes)
There are two ways we could choose one bolt and one nut: we could choose a bolt first and a nut second, or we could choose a nut first and a bolt second. Each of these choices corresponds to one desired outcome.
To find the number of ways to choose a bolt first and a nut second, we multiply the number of bolts (3) by the number of nuts (3), since there are 3 possible bolts and 3 possible nuts to choose from. This gives us 3 x 3 = 9 total outcomes.
Similarly, there are 3 x 3 = 9 total outcomes if we choose a nut first and a bolt second.
Therefore, the total number of desired outcomes is 9 + 9 = 18.
The total number of possible outcomes is the number of ways we could choose two parts from the box, which is the number of ways to choose 2 items from a set of 6 items. This is given by the formula:
Total outcomes = (6 choose 2) = (6! / (2! * 4!)) = 15
Putting it all together, we have:
Probability = (number of desired outcomes) / (total number of outcomes)
Probability = 18 / 15
Probability = 1.2
However, this answer doesn't make sense because probabilities should always be between 0 and 1. So we made a mistake somewhere. The mistake is that we double-counted some outcomes. For example, if we choose a bolt first and a nut second, this is the same as choosing a nut first and a bolt second, so we shouldn't count it twice.
To correct for this, we need to subtract the number of outcomes we double-counted. There are 3 outcomes that we double-counted: choosing two bolts, choosing two nuts, and choosing the same part twice (e.g. choosing the same bolt twice). So we need to subtract 3 from the total number of desired outcomes:
Number of desired outcomes = 18 - 3 = 15
Now we can calculate the correct probability:
Probability = (number of desired outcomes) / (total number of outcomes)
Probability = 15 / 15
Probability = 1
So the probability that one chosen part is a bolt and the other chosen part is a nut is 1, or 100%. This makes sense because if we choose two parts at random, we must get one bolt and one nut since there are three of each in the box.
learn more about probability
https://brainly.com/question/30034780
#SPJ11
Related Questions
Are the lines of equations
x = −2 + 2t, y = −6, z = 2 + 6t and
x=−1+t,y=1+t,z=t, t∈ R, perpendicular to each other?
Answers
The given lines of equations are not perpendicular to each other. Therefore, `θ = cos⁻¹(8/(4√10))` which is approximately `28.07°`.Since `θ ≠ 90°`, the given lines of equations are not perpendicular to each other.
Given lines of equations:
x = −2 + 2t, y = −6, z = 2 + 6tx=−1+t,y=1+t,z=t, t∈ R.
Firstly, we need to find the direction vectors of the two given lines.For the first equation,Let `t=1`, then the point on the line is `(-2+2(1), -6, 2+6(1))`=`(0, -6, 8)`.
Let `t=2`, then the point on the line is
\(`(-2+2(2), -6, 2+6(2))`=`(2, -6,\)14)`.T
herefore, direction vector `
\(v1 = (2, -6, 14)-(0, -6, 8)`=`(2, 0, 6)`\)
For the second equation, direction vector \(`v2 = (1, 1, 1)`.\\\)
Let the angle between the direction vectors `v1` and `v2` be `θ`.
Then, we know that `v1 • v2 = |v1||v2| cosθ`, where `•` represents the dot product of the vectors, and `|.|` represents the magnitude of the vector.
Thus, we have:
(2, 0, 6) • (1, 1, 1) = √(2²+0²+6²)√(1²+1²+1²) cosθ
=> 8 = √40√3 cosθ=> cosθ = 8/(4√10)
Therefore,
`θ = cos⁻¹(8/(4√10))`
which is approximately `28.07°`.
Since `θ ≠ 90°`, the given lines of equations are not perpendicular to each other.
To know more about equations visit :-
https://brainly.com/question/29657983
#SPJ11
A bus drives for 3½ hours at an average speed of 56 mph. How far does the bus drive?
Answers
distance = speed x time
where speed is given in miles per hour (mph) and time is given in hours.
In this case, the speed of the bus is 56 mph and the time it travels is 3.5 hours. So we can calculate the distance it travels as:
distance = speed x time
distance = 56 mph x 3.5 hours
distance = 196 miles
Therefore, the bus drives a distance of 196 miles.
Answer:
196 miles
Step-by-step explanation:
To find the distance that the bus drives, we can use the formula:
distance = rate x time
where rate is the average speed and time is the duration of the trip.
In this case, the average speed of the bus is 56 mph and the duration of the trip is 3 1/2 hours. However, it is easier to work with time in terms of a single unit, so let's convert 3 1/2 hours to 7/2 hours:
3 1/2 hours = (2 x 3) + 1/2 hours = 7/2 hours
Now we can plug in the values into the formula:
distance = rate x time
distance = 56 mph x 7/2 hours
We can simplify by multiplying 56 by 7 and then dividing by 2:
distance = (56 x 7) / 2 = 196 miles
On the image, what is the radius and center of the graphed circle?
(x + 4)^2 + (y - 1)^2 = 3^2
Answers
The radius of the circle as given is; 3.
The center of the circle as given is; (-4, 1).
What is the center and radius of the circle?It follows from the task content that the center and radius of the given circle image and radius are to be determined.
Recall, the center-radius equation of a circle takes the form;
(x - h)² + (y - k)² = r² where center is; (h, k) and radius is r.
By observation of the graph as well as the given equation of the circle, the pair of coordinates for the center is; (-4, 1).
Also, since the radius is the distance from the center to any point on the circumference of the circle; the radius of the circle is; 3.
Read more on center and radius of a circle;
https://brainly.com/question/29614115
#SPJ1
18m = 36
Please help me with this for brainliest HURRYYYY
Answers
Answer: m=2
Step-by-step explanation: Hope this help :D
Let's solve your equation step-by-step.
18m=36
Step 1: Divide both sides by 18.
18m/18=36/18
m=2
Find a sinusoidal function with the following four attributes: (1) amplitude is 10, (2) period is 5, (3) midline is y = 31, and (4) ƒ(3) = 41. f(x) = =
Answers
The sinusoidal function that satisfies the given attributes is f(x) = 10 * sin(2π/5 * x - π/5) + 31.
To find a sinusoidal function with the given attributes, we can use the general form of a sinusoidal function:
f(x) = A * sin(Bx + C) + D
where A represents the amplitude, B represents the frequency (related to the period), C represents the phase shift, and D represents the vertical shift.
Amplitude: The given amplitude is 10. So, A = 10.
Period: The given period is 5. The formula for period is P = 2π/B, where P is the period and B is the coefficient of x in the argument of sin. By rearranging the equation, we have B = 2π/P = 2π/5.
Midline: The given midline is y = 31, which represents the vertical shift. So, D = 31.
f(3) = 41: We are given that the function evaluated at x = 3 is 41. Substituting these values into the general form, we have:
41 = 10 * sin(2π/5 * 3 + C) + 31
10 * sin(2π/5 * 3 + C) = 41 - 31
10 * sin(2π/5 * 3 + C) = 10
sin(2π/5 * 3 + C) = 1
To solve for C, we need to find the angle whose sine value is 1. This angle is π/2. So, 2π/5 * 3 + C = π/2.
2π/5 * 3 = π/2 - C
6π/5 = π/2 - C
C = π/2 - 6π/5
Now we have all the values to construct the sinusoidal function:
f(x) = 10 * sin(2π/5 * x + (π/2 - 6π/5)) + 31
Simplifying further:
f(x) = 10 * sin(2π/5 * x - 2π/10) + 31
f(x) = 10 * sin(2π/5 * x - π/5) + 31
Therefore, the sinusoidal function that satisfies the given attributes is f(x) = 10 * sin(2π/5 * x - π/5) + 31.
Learn more about sinusoidal function here
https://brainly.com/question/29529184
#SPJ11
A number times six plus the same number times two
Answers
Answer:
6x +2x
Step-by-step explanation:
when the number= x, you can just form the equation as per usual. 6x = a number times 6; 2x = a number times 2.
x is used bc the number is an unknown value. only x can be used bc it is stated the same number. hsing different alphabets such as y or z indicates the unknown value ia different.
Answer:
\(x ^{2} + 8x + 12\)
Step-by-step explanation:
This works because of the method called "foil"
Ue the given condition to write an equation for the line in point-lope form and in lope-intercept form. Slope = 1/2, paing through the origin
Answers
The equation of the line in point-slope form and in slope-intercept form are both y = 1/2x.
There are three common forms of the equation of a line:1. Point-Slope Form: y - y1 = m(x - x1), where m is the slope of the line and (x1, y1) is a point on the line.
2. Slope-Intercept Form: y = mx + b, where m is the slope of the line and b is the y-intercept.
3. Standard Form: Ax + By = C, where A and B are coefficients that define the slope and y-intercept of the line.
If a line has a slope of 1/2 and passing through the origin, then:
m = 1/2
(x1, y1) = (0,0)
Plug in the values in the point-slope form and in slope-intercept form.
point-slope form
y - y1 = m(x - x1)
y - 0 = 1/2(x - 0)
y = 1/2x
slope-intercept form
y = mx + b
y = 1/2x + b
Substitute the values of x and y and solve for the y-intercept, b.
0 = 1/2(0) + b
b = 0
y = 1/2x + 0
y = 1/2x
Learn more about equation of line here: https://brainly.com/question/6497976
#SPJ4
the current temperature in small town is 20 degrees fahrenheit this is 6 degrees less than twice the temperature that it was 6 hours ago
Answers
a wheat farmer is investigating the effectiveness of a treatment for controlling a pest. a random sample of 500 plants shows that 47 of them are infected by the pest. what does this sample indicate about the claim that 20% of the plants are infected?
Answers
The sample indicates that the data does not provide sufficient evidence to support the claim that 20% of plants are infected.
This given test is a test for single sample proportion
The test hypothesis are:
\(H_{o} :p=0.20\), null hypothesis
\(H_{1} :p\neq 0.20\), alternative hypothesis
The test statistic fallows a standard normal distribution and is given by:
\(Z=\frac{x-p}{{\sqrt{p(1-p)/n} } }\)
p=0.20
X=47 plants
Sample size, n=500
x, is the sample mean:
x=X/n=47/500
x=0.094
So, test statistic is calculated as:
\(Z=\frac{0.094-0.20}{\sqrt{0.20(1-0.20)/500} }\)
Z=-5.93
From the z-table, the p-value associated with Z=-5.93 is approximately 0
The decision rule based on p-vale, is to reject the null hypothesis if p-value is less than confidence level
In this case, the p-value is very small and less than confidence level of 0.20, we therefore reject the null hypothesis or the claim
So we conclude that the data does not provide sufficient evidence to support the claim that 20% of plants are infected.
To learn more about claims and hypothesis test; click here:
https://brainly.com/question/17134633
#SPJ4
answer the question below which equation describes the function whose y-intrercept is -3 and whose graph has slope 5A) y=-3×+5B)y=3×-5c)y=5×-3D)y=5×+3
Answers
Answer:
C) y = 5x - 3
Explanation:
The equation of a line has the following form:
y = mx + b
Where m, the number beside x, is the slope and b is the y-intercept.
So, if the y-intercept is -3 and the slope is 5, the equation that describes the function is:
y = 5x - 3
So, the answer is y = 5x - 3
Will Mark Brainlest Help Please ,,,,
find the value of x and y
Answers
\(\\ \sf\longmapsto 2x+y=2\)
\(\\ \sf\longmapsto 2x=2-y\)
\(\\ \sf\longmapsto x=\dfrac{2-y}{2}\dots(1)\)
And
\(\\ \sf\longmapsto x+1=y+2\)
\(\\ \sf\longmapsto x=y+2-1\)
\(\\ \sf\longmapsto x=y+1\)
Put the value
\(\\ \sf\longmapsto \dfrac{2-y}{2}=y+1\)
\(\\ \sf\longmapsto 2-y=2(y+1)\)
\(\\ \sf\longmapsto 2-y=2y+2\)
\(\\ \sf\longmapsto 2-2=2y+y\)
\(\\ \sf\longmapsto 3y=0\)
\(\\ \sf\longmapsto y=\dfrac{0}{3}\)
\(\\ \sf\longmapsto y=\infty\)
Put in eq(1)
\(\\ \sf\longmapsto x=\dfrac{2-y}{2}\)
\(\\ \sf\longmapsto x=\dfrac{2-\infty}{2}\)
\(\\ \sf\longmapsto x=\dfrac{2}{2}\)
\(\\ \sf\longmapsto x=1\)
Which graph represents the function f x equals four over X?.
Answers
Answer:
You can see the graph in the picture attached.
city water tank holds 20 gallons of water. A technician empties 25% of the tank. How many more gallons of water must be removed from the tank so that it has 2/5 of the water that it started with?
Answers
Answer:
7
Step-by-step explanation:
Calcilate the fusere valo of 57,000 in 2. 5 years at an interest rale of \( 5 \% \) per year. b. 10 year at an irterest rate of \( 5 \% \) per year e. 5 years at an irterest rate of 10 h per year. a.
Answers
Answer:
Step-by-step explanation: I am sorry but i don't understand a single thing:(
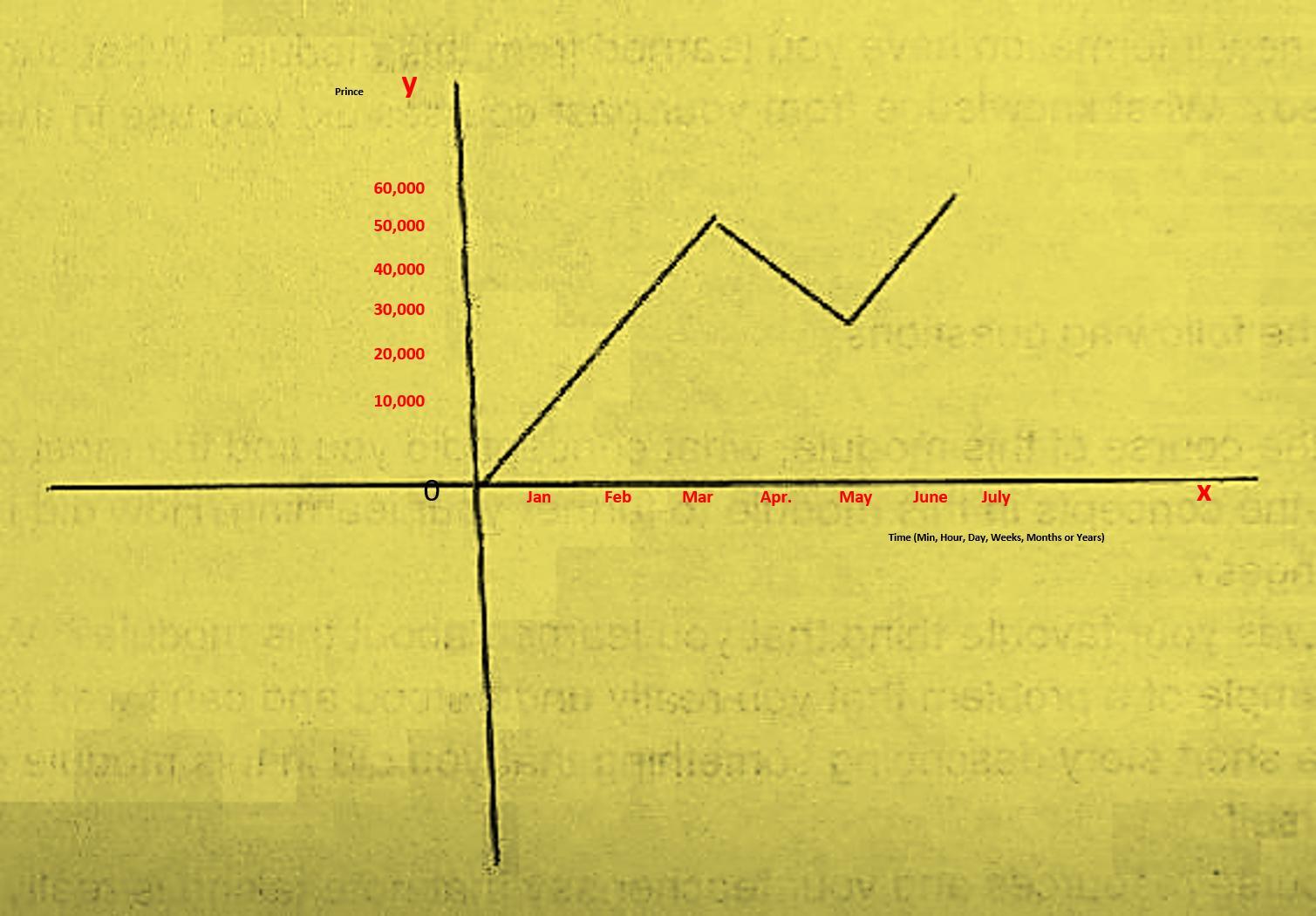
Part 1 - Application Pick one of the two graphs below. Describe a situation which could be modeled by this polynomial graph. Be sure to label the x and y axis with what each will represent in your real life graph. Sample labels could include time, temperature, speed, distance and more. Be sure to add numbers to your axes as well and explain how you came up with your situation.
Answers
One good example of a situation that can be modeled by this Polynomial Graph is the price-time relationship between currency pairs being traded on the Foreign Exchange Market.
What is a Polynomial Graph?A polynomial parameter graph is essentially a smooth continuous curve.
Although the forex graph attached has sharp undulations, when regressed and viewed via Polynomial Regression Indicators, they exhibit strong polynomial qualities that meet the requirements of the definition above.
It is to be noted that the Y-Axis is indicative of the price of the currency pairs (which could be any currency against another) and the X-Axis expresses time. See the attached graphs for a better picture.
Learn more about polynomial graphs at:
https://brainly.com/question/9696642
#SPJ1
Solve 3x2 + 2 = −x by using the Quadratic Formula. If necessary, round to the nearest hundredth. x ≈ 9.46 or x ≈ 2.54 x ≈ 6.58 or x ≈ 5.42 There are no real solutions. x ≈ 1.58 or x ≈ 0.42
Answers
There are no real solutions.
negitive ten is no less than two times a number plus fourteen
Answers
Answer:
Negative 12
Step-by-step explanation:
-10 ≥ 2x + 14
-24 ≥ 2x [subtract 14 from both sides]
2x ≤ -24 [read right to left]
x ≤ -12 [divide both sides by 2]
help meeeeeeeeeeee pleaseee rnnnnn!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Answers
By evaluating the exponential equation, we will see that the amount that Erica owes after 6 years is $8551.56
How to find the amount owed after 6 years?Here we just need to use the exponential equation:
A = P*(1 + r/n)^(n*t)
Where A represents the amount owed t years after, and the other letters represent:
P is the initial amount, here we know that it is $5,300, so P = $5,300r is the rate of growth, which is the percentage written as a decimal, so here we have r = 0.08t is the variable, we already said that this is time in years, here we want to find the amount that Erica owes after 6 years, so t = 6.n is how many times the rate applies on one unit of t, in this case the rate is monthly, and there are 12 months in a year, so n = 12.Replacing all that in the given quadratic equation we will get:
A = $5,300*(1 + 0.08/12)^(12*6) = $8551.56
Then the amount that Erica owes is $8551.56
Learn more about exponential equations:
https://brainly.com/question/11832081
#SPJ1
Please Show Work
.......................
Answers
correct answer:
3x + 2 = 35
3x = 35 -2
3x = 33
3x 33
—— = ——
3 3
x = 11
RIGHT ANSWER GETS BRAINLIST 100 POINTS
Samir is working on a project and has cut a number of wooden blocks of equal size that are represented by this right rectangular prism. He now needs to cover the wooden blocks on all sides with a blue fabric.
How much fabric does Samir need in order to cover 5 of these blocks?
12 cm²
34 cm²
60 cm²
170 cm²
Answers
Answer:
170 cm
Step-by-step explanation:
2 * 1 1/2 * 2 = 6
1 1/2 * 4 * 2 = 12
2 * 4 * 2 = 16
In total: 6 + 12 + 16 = 34.
Samir needs to cover 5 of these blocks so: 34 x 5 = 170
I also did the quiz.
Answer: 170cm
Step-by-step explanation: I did the test!! From k12
find a linear equation satisfying the condition, if possible passes through (−2,1) and (0,5)
Answers
A linear equation passing through (−2,1) and (0,5) is y = 2x + 5.
Given two points, (-2,1) and (0,5) on a coordinate plane. The linear equation for the line passing through two points (x₁, y₁) and (x₂, y₂) can be represented using the slope-intercept form given as y-y₁= m(x-x₁), where m is the slope of the line.
Using the two given points to calculate the slope of the line; m = (y₂ - y₁)/(x₂ - x₁)= (5 - 1)/(0 - (-2))= 4/2= 2. Therefore, the slope of the line is 2. Using the slope-intercept form of a line equation; y = mx + b, where m is the slope and b is the y-intercept and substitute slope and either point (0,5) to calculate b.
y = mx + by = 2x + b => 5 = 2(0) + bb = 5
Thus, the linear equation passing through (−2,1) and (0,5) is y = 2x + 5.
Learn more about linear equation here:
https://brainly.com/question/29111179
#SPJ11
can someone help me with this problem? Thank you!
Answers
To find the perimeter add all the sides together.
15 + 8 + 9 + 14 + 12 = 58 in.
Answer: 58 in.
Answer:
Perimeter = 58 inches
Step-by-step explanation:
Given side measures;
15 inches12 inches14 inches9 inches8 inchesThe perimeter of the figure is the sum of the measure of its sides. Therefore, the perimeter of the figure will be represented as;
⇒ 15 inches + 12 inches + 14 inches + 9 inches + 8 inchesCalculations:1. Add 15 and 14 in the expression
⇒ 29 inches + 12 inches + 9 inches + 8 inches [15 + 14 = 29]2. Add 12 and 9 in the expression
⇒ 29 inches + 21 inches + 8 inches [12 + 9 = 21]3. Add 21 and 29 in the expression
⇒ 50 inches + 8 inches [21 + 29 = 50]4. Add 50 and 8 in the expression
⇒ 58 inches [50 + 8 = 58]Therefore, the perimeter of the figure is 58 inches.
If n items are arranged two at a time, the number obtained is 20. Find the value of n.
Answers
Answer:
\(\tt ^{n}P_{2} = \dfrac{n \: !}{(n - 2)!} = 20\)
\(\tt \dfrac{n(n - 1)(n - 2) \: !}{(n - 2)!} = 20\)
\( \tt n (n - 1)= 20\)
\(\tt n^{2} - n - 20 = 0\)
\(\tt n^{2} - 5n + 4n -20 = 0\)
\(\tt n(n - 5) + 4(n -5) = 0\)
\(\tt n = 5 \: or \: n = - 4\)
Therefore, value of n = 5.
5. h(x)=0.5x - 1 with domain (-♾, 4) what is the range
Answers
We have a domain of a function, that is, which x-es can we throw in. But we are asking which y-s will we get given that we can only throw x-es in \((-\infty,4)\).
Let's try \(x=4\) even though we are forbidden to put 4 inside \(h\) we are still able to do so.
So \(h(4)=0.5\cdot4-1=2-1=1\) what we just got is the upper limit of the range. The lower limit is \(h(-\infty)=-\infty\).
So the range is just \((-\infty, 1)\).
Hope this helps :)
2x + 5 =12
What is x
Answers
Answer:
7/2
Step-by-step explanation:
2x=12-5....collectible like terms
2x=7
x=7/2...dividing both side by 2
Answer:
soln
we know that,
2x + 5 = 12
or, 2x = 12 - 5
or, 2x = 7
or, x = 7/2
x=7/2
need help with this please!
Answers
Answer:
p = 19 ft
hope it's helpful
Help me or I’ll kith you
Answers
Answer:
The answer is (-2,10)
What are the domain restrictions of q^2−7q−8 divided by q^2+3q−4 ?
o q≠1 and q≠−8
o q≠−1 and q≠8
o q≠−1 and q≠4
o q≠1 and q≠−4
Answers
The domain restrictions of the expression q²−7q−8/q²+3q−4 are q ≠ -4 and q ≠ 1. (option c)
The denominator of the expression is q²+3q−4. To determine the values that would make the denominator equal to zero, we can set it equal to zero and solve for q:
q² + 3q - 4 = 0
Now, we can factorize the quadratic equation:
(q + 4)(q - 1) = 0
To find the values of q, we set each factor equal to zero and solve for q:
q + 4 = 0 or q - 1 = 0
Solving these equations, we get:
q = -4 or q = 1
So, the values of q that would make the denominator equal to zero are q = -4 and q = 1. These are the values we need to exclude from the domain of the expression to avoid division by zero.
Therefore, the correct answer is option c) q ≠ 1 and q ≠ -4.
To know more about domain here
https://brainly.com/question/28599653
#SPJ4
Complete Question:
What are the domain restrictions of q²−7q−8/q²+3q−4?
a) q≠1 and q≠−8
b) q≠−1 and q≠4
c) q≠1 and q≠−4
d) q≠−1 and q≠8
help help help help with this please
Answers
choose one of the rental properties from part 2. using the dollar amount for savings in part 1, calculate how many months it will take to have four months of rent saved.
Answers
To calculate how many months it will take to have four months of rent saved for a chosen rental property, we need specific information about the rental property's monthly rent.
To determine the number of months required to save four months of rent, we divide the total savings amount from Part 1 by the monthly rent of the chosen rental property. This will give us the number of months it will take to accumulate the equivalent of four months' rent. By knowing the specific monthly rent, we can divide the savings amount by the monthly rent and obtain the answer in terms of months. Please provide the monthly rent, and I will perform the calculation for you.
Learn more about numbers here: brainly.com/question/24908711
#SPJ11