Three friends go grocery shopping together, and each buys the same kind of
oranges. LaMar buys 2 pounds (lb) and pays $1.00. Enrico buys 4 pounds and
pays $2.00. Anna buys 3 pounds and pays $1.50.
Identify the aranh and unit price that represent the orange costs.

Answers
Answer: C In my case
Step-by-step explanation:
Well you wanna choose the one with 1,2,3,4 as its pounds and that should be correct with the 50 cents in dollars.
Related Questions
113-5.[ 2 3-( 2 3+(6))]
Answers
Answer:
143 should be correct
Step-by-step explanation:
hope this helps
A jeepney ride cost 11 pesos for the first 4 kilometers and each additional integer kilometers adds 3.50 pesos to the fare, use a piece-wise function to represent the jeepney fare in terms of the distance f(d) in kilometers.
Answers
Answer:
\(f(d)=\left\{ \begin{matrix} 11 & \text{for} & 0< d\leq 4 \\-3+3.5d & \text{for}& d > 4 \end\)
Step-by-step explanation:
Cost of first 4 kilometers ride = 11 pesos.
So, for the first 4 km, the fair is constant i.e.
for 1 km the fare is 11 pesos,
for 2 km the fair is also 11 pesos,
similarly, for 3 km of 4 km, the fare is 11 pesos.
Hence, for the distance \(0\geq d\geq 4\), the fair function,
\(f(d)=11\cdots(i)\)
After 4 km, there is an increment of $ 3.50 for each kilometer.
So, the fare function up to 5 kilometers,
\(f(d)=11+3.5=14.5\)
So, the fare function up to 6 kilometers, i.e for the distance \(5<d\leq6\),
\(f(d)=11+2\times3.5=18\)
This can be arranged as the fare function up to 6 km,
\(f(d)=11+(6-4)\times3.5=18\)
Similarly, the fare function up to \(d\) kilometer \((n>4)\),
\(f(d)=11+(d-4)\times3.5\)
\(\Rightarrrow f(d)=-3+3.5d\cdots(ii)\)
Hence, from equations (i) and (ii),
\(f(d)=\left\{ \begin{matrix} 11 & \text{for}\; 0< d \leq 4 \\-3+3.5d & \text{for}\; d > 4 \end\)
Olivia wants to buy a pizza. A plain cheese pizza costs $8.50 and each additional topping costs $0.75. Let t represent the number of toppings. How many toppings can Olivia get if she only has $8.00 to spend. Set up your inequality and solve. Then write your final answer in a complete sentence.
Answers
Olivia would be able to get 11 toppings.
Steps:
8.00 / .75 = 10.6
Round~
11
You're welcome!!!
You bought some new fish and need the tank ready. You fill the tank with water and start running the filter system.You check the temperature of the water after 2 hours and notice the water is 78 degrees Fahrenheit. You need the temperature to be at 72 degrees Fahrenheit. after three additional hours and the water temperature is at so, you add the fish. What was the temperature when you first filled the tank?
Answers
Answer:
82 degrees
Step-by-step explanation:
It took 3 hours for it to go from 78 to 72.
Which is a rate of -2 degrees per hour
We want to know what the temperature was two hours before it was 78 degrees so we'd do 78 - (-2) which is 82
Suppose a life insurance company sells a
$280,000
1-year term life insurance policy to a
20-year-old
female for
$270.
According to the National Vital Statistics Report, 58(21), the probability that the female survives the year is
0.999544.
Compute and interpret the expected value of this policy to the insurance company.
Answers
Answer:
$142.32, profit on sale of the policy
Step-by-step explanation:
You want to know the expected value of a $280,000 life insurance policy sold for $270, if the probability the insured will live for the year is 0.999544.
CostThe insurance company expects to have to pay the $280,000 death benefit for 0.000456 of the policies issued. That means their expected payout on any one policy is ...
0.000456 × $280,000 = $127.68
ProfitThe company gets a premium of $270 for the policy, so the expected value of the policy to the company is ...
$270 -127.68 = $142.32
The expected value of the policy to the company is $142.32.
This represents its profit from sale of the policy.
__
Additional comment
Of course, the company has expenses related to the policy, perhaps including a commission to the agent selling it, and expenses related to handling claims. That is to say that not all of the difference between the premium and the average death benefit is actually profit. It is what might be called "contribution margin."
<95141404393>
help find the missing side

Answers
Answer:
12.9
Step-by-step explanation:
tanθ=opp/adj
tan 24° = x/29
x = 29 tan 24°
x = 12.9
2(x + 1) - 3x=? What is it?
Answers
2x + 2 - 3x = 0
-x + 2 = 0
-x = -2
Divide -1 on both sides
x = 2
What is the factored form of 250x3 − 16?
Answers
Answer:
Step-by-step explanation:
250x^3-16
2(125x^3-8)
2[(5x)^3-(2)^3]
2(5x-3)[(5x)^2+5x*3+(2)^2]
2(5x-3)(25x^2+15x+4)
The diameter of the can of tennis balls is about 3 inches, and the can is 9 inches tall. How much space in the
canister is not taken up by the tennis balls? Write your answer as a decimal rounded to the nearest tenth.
Answers
Answer:
27
Step-by-step explanation:
9x3 right so 27
Which of the following problem types can always be solved using the law of cosines or sines? Check all that apply.A. SSSB. AAAC. ASAD. SAAE. SSAF. SAS
Answers
The law of sines can be solved for the following cases:
• AAS
,• ASA
,• SSA (But this can be ambigous)
The law of cosines can be solved for the following cases:
• SAS
,• SSS
Thererefore, the correct options are A, C, E, D and F
A community is building a square park with side is that measure 120 m to separate the picnic area from the play area the park is split by a diagonal line what is the approximate length of the diagonal line
Answers
Answer:
(120^2+120^2)^0.5 = 169.705m
Step-by-step explanation:
Pythagorean Theorem
What is the mean of the values in the stem-and-leaf plot?
Enter your answer in the box.

Answers
Answer:
mean = 24
Step-by-step explanation:
the mean is calculated as
mean = \(\frac{sum}{count}\)
the sum of the data set is
sum = 12 + 13 + 15 + 28 + 28 + 30 + 42 = 168
there is a count of 7 in the data set , then
mean = \(\frac{168}{7}\) = 24
A box with a hinged lid is to be made out of a rectangular piece of cardboard that measures 3 centimeters by 5 centimeters. Six squares will be cut from the cardboard: one square will be cut from each of the corners, and one square will be cut from the middle of each of the -5 centimeter sides . The remaining cardboard will be folded to form the box and its lid . Letting x represent the side-lengths (in centimeters) of the squares, to find the value of that maximizes the volume enclosed by this box. Then give the maximum volume. Round your responses to two decimal places.
Answers
Answer:
The volume of the box is maximized when x = 0.53 cm
Therefore, x = 0.53 cm and the Maximum volume = 1.75 cm³
Step-by-step explanation:
Please refer to the attached diagram:
The volume of the box is given by
\(V = Length \times Width \times Height \\\\\)
Let x denotes the length of the sides of the square as shown in the diagram.
The width of shaded region is given by
\(Width = 3 - 2x \\\\\)
The length of shaded region is given by
\(Length = \frac{1}{2} (5 - 3x) \\\\\)
So, the volume of the box becomes,
\(V = \frac{1}{2} (5 - 3x) \times (3 - 2x) \times x \\\\V = \frac{1}{2} (5 - 3x) \times (3x - 2x^2) \\\\V = \frac{1}{2} (15x -10x^2 -9 x^2 + 6 x^3) \\\\V = \frac{1}{2} (6x^3 -19x^2 + 15x) \\\\\)
Take the derivative of volume and set it to zero.
\(\frac{dV}{dx} = 0 \\\\\frac{dV}{dx} = \frac{d}{dx} ( \frac{1}{2} (6x^3 -19x^2 + 15x)) \\\\\frac{dV}{dx} = \frac{1}{2} (18x^2 -38x + 15) \\\\\frac{dV}{dx} = \frac{1}{2} (18x^2 -38x + 15) \\\\0 = \frac{1}{2} (18x^2 -38x + 15)\\\\18x^2 -38x + 15 = 0\\\\\)
We may solve the quadratic equation using the quadratic formula.
\($x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$\)
The values of coefficients a, b, c are
\(a = 18 \\\\b = -38 \\\\c = 15 \\\\\)
Substituting the values into quadratic formula yields,
\(x=\frac{-(-38)\pm\sqrt{(-38)^2-4(18)(15)}}{2(18)} \\\\x=\frac{38\pm\sqrt{(1444- 1080}}{36} \\\\x=\frac{38\pm\sqrt{(364}}{36} \\\\x=\frac{38\pm 19.078}{36} \\\\x=\frac{38 + 19.078}{36} \: or \: x=\frac{38 - 19.078}{36}\\\\x= 1.59 \: or \: x = 0.53 \\\\\)
Volume of box when x = 1.59:
\(V = \frac{1}{2} (5 - 3(1.59)) \times (3 - 2(1.59)) \times (1.59) \\\\V = -0.03 \: cm^3 \\\\\)
Volume of box when x = 0.53:
\(V = \frac{1}{2} (5 - 3(0.53)) \times (3 - 2(0.53)) \times (0.53) \\\\V = 1.75 \: cm^3\)
As you can see, the volume of the box is maximized when x = 0.53 cm
Therefore, x = 0.53 cm and the Maximum volume = 1.75 cm³

A lot of 1000 components contains 350 that are defective. Two components are drawn at random and tested. Let A be the event that the first component drawn is defective, and let B be the event that the second component drawn is defective.
a. Find P(A).b. Find P(B|A) .c. Find P(A ∩ B).d. Find P(Ac ∩ B).e. Find P(B) .f. Find P(A|B).g. Are Aand B independent? Is it reasonable to treat A and B as though they were independent? Explain.
Answers
The probabilities are:
a. P(A) = 0.35
b. P(B|A) ≈ 0.349
c. P(A ∩ B) ≈ 0.122
d. P(A^c ∩ B) ≈ 0.228
e. P(B) = 0.35
f. P(A|B) = 0.349
g. A and B are independent.
Yes, it is reasonable to treat A and B as though they were independent because P(A) * P(B) = P(A ∩ B).
We have,
Given:
Total number of components (n) = 1000
Number of defective components (d) = 350
a.
P(A) is the probability that the first component drawn is defective:
P(A) = d/n = 350/1000 = 0.35
b.
P(B|A) is the probability that the second component drawn is defective given that the first component drawn is defective:
Since one defective component has already been drawn, the total number of components is now 999, and the number of defective components remaining is 349.
P(B|A) = Number of defective components remaining / Total number of components remaining = 349/999 ≈ 0.349
c.
P(A ∩ B) is the probability that both the first and second components drawn are defective:
P(A ∩ B) = P(A) * P(B|A) = 0.35 * 0.349 ≈ 0.122
d.
P(\(A^c\) ∩ B) is the probability that the first component drawn is not defective (complement of A) and the second component drawn is defective:
\(P(A^c)\) is the probability that the first component drawn is not defective:
\(P(A^c)\) = 1 - P(A) = 1 - 0.35 = 0.65
Since the first component drawn is not defective, the total number of components remaining is now 999, and the number of defective components remaining is still 350.
P(\(A^c\) ∩ B) = P(\(A^c\)) * P(B) = 0.65 * (350/999) ≈ 0.228
e.
P(B) is the probability that the second component drawn is defective:
P(B) = Number of defective components / Total number of components
= 350/1000
= 0.35
f.
P(A|B) is the probability that the first component drawn is defective given that the second component drawn is defective:
P(A|B) = P(A ∩ B) / P(B)
= (0.35 * 0.349) / 0.35
= 0.349
g.
To determine if A and B are independent, we need to compare
P(A) * P(B) with P(A ∩ B).
P(A) * P(B) = 0.35 * 0.35 = 0.1225
P(A ∩ B) = 0.122
Since P(A) * P(B) = P(A ∩ B), A and B are independent events.
It is reasonable to treat A and B as independent because the probability of A and the probability of B are not affected by each other.
The occurrence or non-occurrence of A does not impact the probability of B.
Thus,
The probabilities are:
a. P(A) = 0.35
b. P(B|A) ≈ 0.349
c. P(A ∩ B) ≈ 0.122
d. P(A^c ∩ B) ≈ 0.228
e. P(B) = 0.35
f. P(A|B) = 0.349
g. A and B are independent.
Yes, it is reasonable to treat A and B as though they were independent because P(A) * P(B) = P(A ∩ B).
Learn more about probability here:
https://brainly.com/question/14099682
#SPJ4
please help
What is the distance to the earth’s horizon from point P?
Enter your answer as a decimal in the box. Round only your final answer to the nearest tenth.
x =
mi

Answers
The measure of distance x, that is, the distance between a point P and the point of horizon, is equal to 284.372 miles.
How to find the distance to the earth horizon from a given point
In this problem we must determine the distance between a point P located about earth's circumference and the point of horizon, located on earth's circumference. Since the line between these two points is tangent to earth, then, distance x can be found by Pythagorean theorem:
x = √[(3959 mi + 10.2 mi)² - (3959 mi)²]
x = 284.372 mi
The distance x is equal to 284.372 miles.
To learn more on Pythagorean theorem: https://brainly.com/question/14930619
#SPJ1
if the distance between the points (5, 2) and (9, a) is 25 units then find the value of a?
Answers
Answer:
15 just the answer because of the value given above
Answer: Value of A is 5.
Step-by-step explanation:Can someone help me please it's only 2 questions!!!!!


Answers
Problem 1
Answer: -4 + 7Reason: We start at 0 and move 4 units left. This is represented by 0+(-4) or 0-4. That simplifies to -4. Then add on 7 to move 7 units to the right to arrive at 3 as the final destination.
=============================================
Problem 2
Answer: 8 + 3Reason: We start at 0 and move 8 units to the right. That is represented by +8 or simply 8. Then the +3 will move us 3 more units to the right to get to 11 on the number line. This is one visual way to see why 8+3 = 11.
8 is what percent of 24?
What is 63% of 130?
36 is 15% of what number?
A farmer decides to sell 32 pounds of his small 96 pound potato crop. What percent of the crop did he sell?
A university has 480 female students. This represents 64% of the student body. How many students are enrolled in the university?
Answers
Answer:
1, 33.3
2, 81.9
3, 240
4, the farmer sold 33.3 of his crops
5, 750 students are enrolled.
Answer:
1. 8 is 33.3333333% of 24. 2. 63% of 130 is 81.9. 3. 36 is 15% of 240. 4. 30.72% of crops. 5. 750 students
Step-by-step explanation:
Hope this helped you!! Give brainliest.
What is the value of 6 in 573,6007
600
6,000
0,6
0,060
Answers
Josie makes fruit punch by mixing fruit juice and lemonade in the ratio 1:3
She needs to make 28 litres of punch for a party,
How much of each ingredient does she need?
Fruit juice = 7 litres Lemonade = 21 litres [4]
During the party Josie decides to make some more.
She has 3 litres of fruit juice left and plenty of lemonade,
How much extra punch can she make?
litres
To make the second batch of punch go further Josie
adds 3 more litres of lemonade,
What is the ratio of fruit juice to
lemonade in the second batch?
Answers
For the second batch the ratio of fruit juice to lemonade would be 3:12 or 1:4
If g(x) = x2 + 3, find g(4).
11
19
16
8
Answers
4^2=16
16+3=19
If triangles ABC and DEF are similar, what is y? Show your work.

Answers
The value of y is 18
What are similar triangles?Similar triangles have the same corresponding angle measures and proportional side lengths. The angles of the two triangle must be equal and it not necessary they have equal sides.
Therefore the corresponding angles of similar triangles are congruent and the ratio of corresponding sides of similar triangles are equal.
Therefore;
14/21 = 12/y
14y = 21 × 12
14y = 252
divide both sides by 14
y = 252/14
y = 18
Therefore the value of y is 18.
learn more about similar triangles from
https://brainly.com/question/14285697
#SPJ1
What is the value of p?
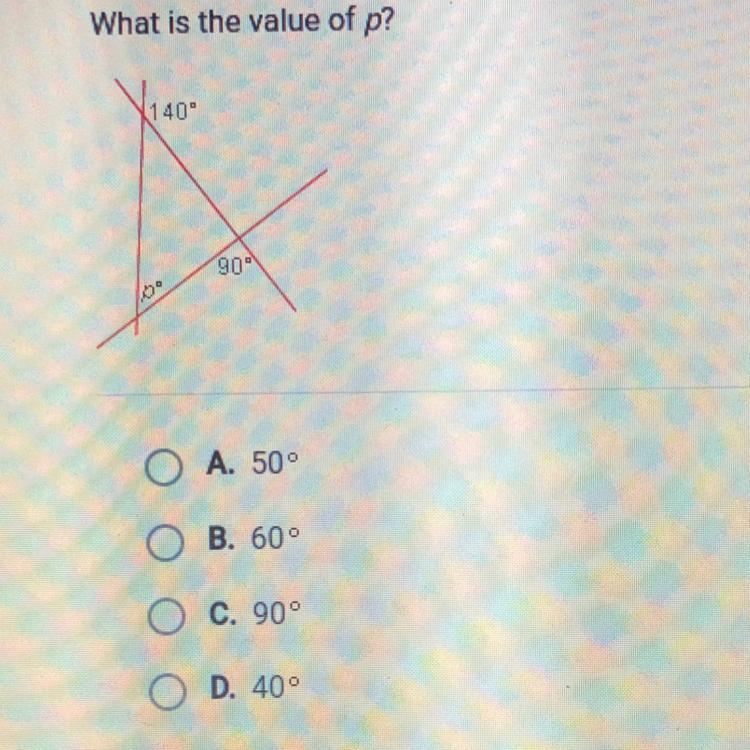
Answers
Answer:
Not C, Not A, most likely B
Step-by-step explanation:
Its less than 90 because its and acute, meaning its smaller, so you can already knock off C.
Match each expression with A, B, C or D.
A=a^3
B=6a
C=12a
D=3a^2
i)3a x 4
ii)a^2xa
iii) 6 1/2 a^2

Answers
The matching expressions are:
\(i) 3a x 4 = C (12a)\\ii) a^2 x a = A (a^3)\\iii) 6 × 1/2 a^2 = D (3a^2)\)
i) 3a x 4 can be represented as C (12a) since multiplying 3a by 4 gives 12a.
ii) a^2 x a can be represented as A (a^3) since multiplying a^2 by a gives a^3.
iii) \(6 \times 1/2 a^2\) can be represented as D (3a^2) since multiplying 6 by 1/2 and then by a^2 gives 3a^2.
To understand the matching expressions, let's break down each one:
i) 3a x 4:
This expression represents multiplying a variable, 'a', by a constant, 4. The result is 12a, which matches with C (12a).
ii) a^2 x a:
This expression represents multiplying the square of a variable, 'a', by 'a' itself. This results in a^3, which matches with A (a^3).
iii) 6 × 1/2 a^2:
This expression involves multiplying a constant, 6, by a fraction, 1/2, and then multiplying it by the square of 'a', a^2. The final result is 3a^2, which matches with D (3a^2).
Therefore, the matching expressions are:
i) 3a x 4 = C (12a)
ii) a^2 x a = A (a^3)
iii) 6 × 1/2 a^2 = D (3a^2)
for such more question on matching expressions
https://brainly.com/question/12270624
#SPJ8
Compound Interest
When Jack turned 21, he decided to start investing $200 a month every year for nine years. At age 30, he decided to stop investing altogether.
Blake started a little later, investing $200 a month every month starting at age 30, all the way until the ripe old age of 67.
Assuming that they were both amazing at investing and made 11% interest per year, how much money will they both have at age 67?
Answers
Answer:
Jack $1800 Blake $7400
Step-by-step explanation:
What is the definition of deductive reasoning?
Answers
Answer:
Deductive reasoning is a method of logical thought that begins with a general concept and arrives at a particular conclusion. It is often referred to as top-down thought or shifting from general to particular.
Step-by-step explanation:
Here are some examples:
Elephants have cells in their bodies, and all cells have DNA. ...All horses have manes.Acute angles are less than 90 degrees. This angle is 40 degrees, so it must be an acute angle.All noble gases are stable.deductive reasoning is a type of logical thinking that starts with the general idea and reaches a specific conclusion
Solve the following absolute value equation for the unknown. Show all of your work for full credit. |-3h – 6| ≤ 3
Answers
Answer:
\(-3 \le h \le 1\).
Step-by-step explanation:
Apply the property of absolute values: if \(a \ge 0\), then \(|x| \le a \iff -a \le x \le a\). By this property, \(|- 3\, h - 6 | \le 3\) is equivalent to \(-3 \le -3\, h - 6\le 3\). That's the same as saying that \(-3\, h - 6 \ge -3\) and \(-3\, h - 6 \le 3\).
Add \(6\) to both sides of both inequalities:
\(-3\, h \ge 3\) and \(-3\, h \le 9\).
Divide both sides of both inequalities by \((-3)\). Note that because \(-3 < 0\), dividing both sides of an equality by this number will flip the direction of the inequality sign.
\(-3\, h \ge 3\) would become \(h \le -1\).\(-3\, h \le 9\) would become \(h \ge -3\).Both inequalities are supposed to be true. Combining the two inequalities to obtain:
\(-3 \le h \le 1\).
Find the area of the isosceles trapezoid.
10 cm
9 cm
18 cm
OA.126 cm²
OB.91 cm²
OC. 252 cm²
OD. 63 cm2

Answers
Step-by-step explanation:
therefore, the correct option should be A.

a. Find parametric equations and symmetric equations for the line passing through the points (-2, 4, 3) and (1, 2, 7).
b. At what point does this line intersect the yz-plane?
Answers
a) The parametric equations of the line are: x(t) = −2 + 3t, y(t) = 4 − 2t, z(t) = 3 + 4t and The symmetric equation of the line are: (x + 2)/3 = (y − 4)/−2 = (z − 3)/4
b) The line intersects yz-plane at (0, 8/3, 17/3)
The given points on the line are:
(x₁, y₁, z₁) = (−2, 4, 3)
(x₂, y₂, z₂) = (1, 2, 7)
The direction ratios of this line are:
⟨a, b, c⟩ = ⟨x₂ − x₁, y₂ − y₁, z₂ − z₁⟩
= ⟨1 + 2, 2 − 4, 7 − 3⟩
= ⟨3, −2, 4⟩
a) Parametric equations of the line:
These are given by:
x(t) = x₁ + at = −2 + 3t
y(t) = y₁ + bt = 4 − 2t
z(t) = z₁ + ct = 3 + 4t
Symmetric equation of the line:
This is given by:
(x − x₁)/a = (y − y₁)/b = (z − z₁)/c
(x + 2)/3 = (y − 4)/−2 = (z − 3)/4
b) When a line intersects the yz-plane, its x-coordinate is zero.
Using the parametric equations of the part (a):
x = 0
−2 + 3t = 0
3t = 2
t = 2/3
Substitute this in the parametric equations corresponding to y and z as well:
y = 4 −2t
= 4 − 2(2/3)
= 8/3
z = 3 + 4t
= 3 + 4(2/3)
= 17/3
Hence, the required point is: (x, y, z) = (0, 8/3, 17/3)
To learn more about parametric equations here:
brainly.com/question/28537985
#SPJ4
Part of the population of 8,000 elk at a wildlife preserve is infected with a parasite. A random sample of 50 elk shows that 7 of them are infected. How many elk are likely to be infected?
Answers
From the sample we conclude that:
\(\frac{7}{50}=\text{0}.14\)the probability of an elk being infected is 0.14.
To find out how many of the total are infected we multiply the total by this probability, then:
\(8000\cdot0.14=1120\)Therefore, 1120 elks are likely to be infected.