Triangle ABC has the three angle side lengths of 2.1, 2.1 and 2.1. What is the angle measure of <A.
Is it ABC OR D
A- 2.1
B- 20
C-60
D- 180
Answers
Answer: C) 60
Explanation:
All equilateral triangles are also equiangular. This means all three angles are the same measure. If x was that measure, then
x+x+x = 180
3x = 180
x = 180/3
x = 60
Each angle is 60 degrees
Related Questions
In a complete paragraph, pick a scenario where concepts from this algebra course would be used - it could be in your own life, it could be in a specific work field such as a construction worker, or working in a business, etc. Choose at least 2-3 concepts to include, explain your scenario, how these concepts apply, and provide a worked example for each concept. Use the following format: Topic Sentence: 1 concise sentence describing a scenario where concepts from this course could be used. Supporting Detail: 1-2 sentences explaining how 1 concept from the class can be applied to the scenario. Worked Example: Show a worked example for the concept described above. Supporting Detail: 1-2 sentences explaining how 1 concept from the class can be applied to the scenario. Worked Example: Show a worked example for the concept described above. Conclusion: 1-2 sentences describing how applying the concepts in this algebra course to a real-life situation helps in understanding the material in the course.
Answers
Scenario: A small business owner needs to analyze their sales data to make informed decisions about pricing and profitability.
Supporting Detail 1: The concept of linear equations can be applied to determine the break-even point and set optimal pricing strategies for the business.
Worked Example 1: Let's say the small business sells a product for $10 each, and the fixed costs (expenses that don't vary with the number of units sold) amount to $500. The variable costs (expenses that depend on the number of units sold) are $2 per unit. We can use the formula for a linear cost equation (C = mx + b) to find the break-even point where revenue equals total costs:
10x = 2x + 500
Simplifying the equation, we get:
8x = 500
x = 500/8
x = 62.5
The break-even point is 62.5 units. Knowing this information, the business owner can make decisions about pricing, cost control, and production targets.
Supporting Detail 2: The concept of systems of equations can be applied to optimize the allocation of resources in the business.
Worked Example 2: Let's consider a scenario where the business owner sells two different products. Product A generates a profit of $5 per unit, while Product B generates a profit of $8 per unit. The business owner has a limited budget of $500 and wants to determine the optimal allocation of resources between the two products. We can set up a system of equations to represent the profit constraints:
x + y = 500 (total budget)
5x + 8y = P (total profit, represented as P)
By solving this system of equations, the business owner can find the optimal values of x and y that maximize the total profit while staying within the budget constraints.
Conclusion: Applying concepts from this algebra course to real-life scenarios, such as analyzing sales data for a small business, helps in understanding the material by providing practical applications. It demonstrates the relevance of algebra in making informed decisions, optimizing resources, and maximizing profitability.
These examples highlight how algebraic concepts enable problem-solving and provide valuable tools for individuals in various fields, including business and entrepreneurship.
For more such questions on profitability
https://brainly.com/question/29982132
#SPJ8
What is 3,700,000 in scientific notation??

Answers
=========================================================
Explanation:
Place a decimal point between the first two digits 3 and 7.
Now ask yourself how you can go from 3.7 back to the original value. Notice we can move the decimal point 6 spots to the right to go from 3.7 back to 3,700,000
Therefore, the exponent over the 10 is 6. The exponent is positive to mean we move the decimal point to the right. If we had a negative exponent, then we'd move left.
You can use a calculator to confirm that 3.7 * 10^6 = 3,700,000
--------------
Side notes:
3,700,000 = 3 million, 7 hundred thousand
3,700,000 = 3.7 million
please help me solve this i’ll mark brainliest

Answers
Answer:
Step-by-step explanation:
From the parallel lines, we know that corresponding angles are congruent, so:
(2y+78) = X
We also know that vertically opposite angles are equal:
X=5y
Substitute for X:
2y+78=5y
Solve:
2x-5x=-78
-3x=-78
x=26
Therefore, the measure of angle WXZ is 26.
Solve for the value of x 3x - 9 + 12 - 6x = -18
Answers
Answer:
x=7
Step-by-step explanation:
\(3x-9+12-6x=-18\)
now let’s put together the like terms
\(3-3x=-18\)
\(-3x=-21\)
now we divide \(-21\) By \(-3\)
the result is
\(x=7\)
Answer:
X=7
Step-by-step explanation:
Verification
\(3(7)-9+12-6(7)=-18\\21-9+12-42=-18\\12+12-42=-18\\24-42=-18\)
\(-18=-18\)
I hope this help.Please give me the brainliest
A microwave was originally sold for $137 and has been marked down to $66. What is the percentage decrease for the microwave? ____%
Answers
The percentage decrease in the price of the microwave is 51.82%.
What is the percentage decrease?Percentage is used to determine the relative value of a digit as a number out of a hundred. The sign that is used to represent percentages is %. In order to express a value as a percentage, multiply the number by 100. Percentage is a measure of frequency.
Percentage decrease = (change in price / initial price) x 100
Change in price = initial price - new price
$137 - $66 = $71
(71/137) x 100 = 51.82%
To learn more about percentages, please check: https://brainly.com/question/25764815
#SPJ1
Can someone help me with this question? Thanks!

Answers
You won't type in the percent sign since it's already taken care of by your teacher.
===========================================================
Explanation:
We know 100% that a fruit was chosen first. That means the three original fruits drops down to 3-1 = 2 fruits.
There are 2 fruits left and 2 vegetables. That gives 2+2 = 4 items to pick from for the second slot.
We have 2 things we want (those vegetables) out of 4 items to pick from. The chances of getting a vegetable here is 2/4 = 1/2 = 0.50 = 50%
------------------
This is an optional section, but here's another way to look at it. This method is slightly longer.
Let A,B,C be the three fruits and D,E be the two vegetables.
Here are all of the ways to have a fruit chosen first followed by a vegetable
AD and AEBD and BECD and CEThere are m = 3*2 = 6 ways to do this.
Now consider all of the ways to have a fruit first (either A,B, or C) and the second slot can be a fruit or a vegetable.
Here are all of the ways to do that
AB, AC, AD, AEBA, BC, BD, BECA, CB, CD, CEEach row has 4 items, so we have n = 3*4 = 12 different ways to have a fruit go first and the second item is a fruit or a vegetable.
Therefore, m/n = 6/12 = 1/2 = 0.5 = 50% is the probability of getting a vegetable second given that a fruit was chosen first.
The midpoint of \overline{\text{AB}}
AB
is M(3, 3)M(3,3). If the coordinates of AA are (2, -1)(2,−1), what are the coordinates of BB?
Answers
Answer:
B(4, 7)Step-by-step explanation:
\(M(3,\,3)\,,\quad A(2,\,-1)\,,\quad B(x_B,\,y_B)\\\\\overline{AM}=\overline{MB}\ \implies\ x_M-x_A=x_B-x_M\ \ \wedge\ \ y_M-y_A=y_B-y_M\\\)
\(3-2=x_B-3\qquad\wedge\qquad 3-(-1)=y_B-3\\\\ 1=x_B-3\qquad\qquad\wedge\qquad\ \ 3+1=y_B-3 \\\\ {}\quad x_B=4\qquad\qquad\wedge\qquad\qquad \ y_B=7\)
Answer:b=(1,−3)
Step-by-step explanation:
25 is 5% of what number?X(Type an integer or a decimal.)
Answers
let 5 % of x is 25
that means
\(x\times\frac{5}{100}=25\)\(\begin{gathered} x\times\frac{5}{100}=25 \\ x=\frac{2500}{5}=500 \\ x=500 \end{gathered}\)so the answer is x = 500.
and it is an integer.
=
Interim Checkpoint: Grade 7 Checkpoint 4 - Part 1
Write an equation that you can use to solve for X.
Enter your answer in the box.
100°
60
Answers
60 is the amazing cool answer XD
5. Find the area enclosed by f(x)=5x(5x 2−1) 3and g(x)=x 2.Sketch the region. Decide whether to integrate with respect to x or y. Show your integral and then the steps to solve it using the Evaluation Theorem. Solve your integral without multiplying out the integrand
Answers
To find the area enclosed by the curves f(x) = 5x(5x^2 - 1)^3 and g(x) = x^2, we integrate with respect to x.
To find the area enclosed by the two curves, we need to find the points of intersection and integrate the difference of the functions between those points.
First, let's find the points of intersection by setting f(x) equal to g(x):
5x(5x^2 - 1)^3 = x^2
Simplifying the equation, we have:
25x^6 - 10x^4 + x^2 = x^2
25x^6 - 10x^4 = 0
Factoring out x^2, we get:
x^2(25x^4 - 10) = 0
This equation has two solutions: x = 0 and x = ±sqrt(2/5).
To determine which interval to integrate over, we can plot the curves and visualize the region.
The graph shows that f(x) is above g(x) for x values between -sqrt(2/5) and sqrt(2/5). Therefore, we will integrate over this interval.
The integral to find the area is given by:
A = ∫[x=-sqrt(2/5)]^[x=sqrt(2/5)] (f(x) - g(x)) dx
Substituting the functions f(x) and g(x) into the integral, we have:
A = ∫[x=-sqrt(2/5)]^[x=sqrt(2/5)] (5x(5x^2 - 1)^3 - x^2) dx
Evaluating this integral requires some algebraic manipulation and the use of the Evaluation Theorem, which involves evaluating the antiderivative at the upper and lower limits of integration.
The step-by-step explanation of solving this integral can be quite involved and may require several lines of mathematical expressions and calculations. If you would like me to provide the detailed step-by-step explanation, please let me know.
Learn more about Evaluation Theorem:
brainly.com/question/28155645
#SPJ11
the variance and the standard deviation are examples of measures of the center. group of answer choices true false
Answers
Can someone explain why 12/9 is correct. Will mark brainliest.

Answers
Answer:
Cause u got confused with the numbers you had to switch them up, i dont know what you did wrong but it was the other way around.
Step-by-step explanation:
1
2
Even after that large purchase at Best Buy, you decide to go to Target to grab a few things that you missed. You purchase WWE 2K21 for $49.99, Starbucks Vanilla Coffee for $13.99, the new Keurig K550 for $179.99, and a pair of jeans for $17.99. The state sales tax is 6%.
What is the total selling price before tax?
How much is sales tax did you pay?
What was your total cost?
Answers
The total selling price before tax is $261.96.
The sales tax paid is $15.72.
The total cost is $277.68.
The total selling price before tax is the sum of the prices of the WWE 2K21, Starbucks Vanilla Coffee, new Keurig K550 and the jeans
$49.99 + $13.99 + $179.99 + $17.99 = $261.96.
Sales tax is the amount of money levied when a good or service is purchased. It is a percentage of the price of an item
Sales tax = tax rate x cost
6% x $261.96 = $15.72
The total price paid is the sum of the sales tax and the total selling price.
$15.72 + $261.96 = $277.68
To learn more about taxes, please check: https://brainly.com/question/25311567
[WILL GIVE BRAINLIEST!]
Angle α is in quadrant III and angle β is in quadrant IV. If sin α = –5/6 and cos β = 1/2, find cos(α + β).
Answers
Answer:
Step-by-step explanation:
The expansion for cos(x+y) is cosx*cosy - sinx*siny. We have sin x and cos y, now we need cosx and siny.
Angle x is in QIII and has a sin ratio of -5/6. Since the hypotenuse will never be negative and sin is opposite over hypotenuse, the side across from the reference angle, aka the height of the triangle, is -5 and the hypotenuse is 6. Using Pythagorean's Theorem we can find the third side:
\(6^2=(-5)^2+x^2\) and
\(36=25+x^2\) and
\(36-25=x^2\) so
x = √11.
We do the same for the other angle y. We have the cos of angle y is 1/2 and since the cos ratio is adjacent over hypotenuse, the side next to the reference angle is 1 and the hypotenuse is 2 and we will find the third side using Pythagorean's Theorem:
\(2^2=1^2+y^2\) and
\(4=1+y^2\) and
\(3=y^2\) so
y = √3.
We already know sinx = -5/6, now we know that cosx = -√11/6.
We already know cosy = 1/2, now we know that siny = -√3/2.
Now we can fill in the expansion for cos(x+y):
\((-\frac{\sqrt{11} }{6})(\frac{1}{2})-(-\frac{5}{6})(-\frac{\sqrt{3} }{2})\) Multiplying straight across the top and bottom we get
\(-\frac{\sqrt{11} }{12}-\frac{5\sqrt{3} }{12}\) which simplifies to
\(\frac{-\sqrt{11}-5\sqrt{3} }{12}\)
And you're done!
a cord is a volume of cut wood equal to a stack 8 ft long, 4 ft wide, and 4 ft high. how many cords are in 1.0 m 3 ?
Answers
The number of cords in 1 m^3 are four.
Here , volume of a cuboid is involved. If l, b, h are respectively the length, breadth and the height of the cuboid , then its volume is given by
V = l x b x h cubic units.
Now, here we know that 1 m =3.28 ft.
So, 1 m^3 = (3.28)^3 cubic feet. = 35.288 cubic feet.
So, we have to find the number of cords in 35.288 cubic feet.
Now, volume of a single cord = l x b x h = 8 x 4 x 4 = 128 cubic feet.
So, no. of cord = 128/35.288 = 3.66.
Since, the number of cords is always a whole number , so 3.66 can treated as 4 by rounding it off to unit's place.
Hence, The number of cords in 1 m^3 are four.
To learn more about volume of cuboid, visit link - brainly.com/question/29424737
#SPJ4
The number of cords in 1 m^3 is four.
Here, the volume of a cuboid is involved. If l, b, h are respectively the length, breadth and height of the cuboid, then its volume is given by
V = l x b x h cubic units.
Now, here we know that 1 m =3.28 ft.
So, 1 m^3 = (3.28)^3 cubic feet. = 35.288 cubic feet.
So, we have to find the number of cords in 35.288 cubic feet.
Now, the volume of a single cord = l x b x h = 8 x 4 x 4 = 128 cubic feet.
So, no. of cord = 128/35.288 = 3.66.
Since the number of cords is always a whole number, 3.66 can be treated as 4 by rounding it off to the unit's place.
Hence, The number of cords in 1 m^3 is four.
To learn more about the volume of a cuboid, visit the link - brainly.com/question/29424737
#SPJ4
If jummai is 12years old and Tunde is 8years old and they share 15bananas in the ratio of their ages how many will each have show calculation
Answers
Jummai and Tunde will each have 9 and 6 bananas respectively.
For the given ratio case we use the sharing ratio criterion to solve the problem.
Jummai is 12 years old.
Tunde is 8 years old.
Their ages are in ratio of;
A = 12 : 8
A = 3 : 2
The ratio's sum is 5.
15 bananas total are available for sharing.
Jummai will have \(x\\\) bananas \(x\) = (15 x 3/5) = 9
Tunde will have \(y\) bananas \(y\) = (15 x 2/5) = 6
Jummai and Tunde will each have 9 and 6 bananas with them.
To learn more about Ratio click here:
brainly.com/question/13419413
#SPJ4
Which statement describes how to solve Equation. Square both sides and then solve the resulting quadratic equation.
Square both sides and then solve the resulting cubic equation.
Cube both sides and then solve the resulting quadratic equation.
Cube both sides and then solve the resulting cubic equation.

Answers
Answer:
Cube both sides tham solve the resulting quadratic
The correct statement is:
Cube both sides and then solve the resulting quadratic equation.
What is cube root?The cube root of a number is the factor that we multiply by itself three times to get that number.
Given:
∛(x² - 6) = ∛(2x + 2)
For solving the above equation we have to take cube on both side
x² - 6 = 2x +2
x² - 2x -8 = 0
Then we get the quadratic equation.
Learn more about cube root here:
https://brainly.com/question/12726345
#SPJ5
what is the square root of 35
Answers
Answer:
Step-by-step explanation:
the square root of of 35 is
5.916079783099616
5.9160797831
Step-by-step explanation:
You can round this to 6 as a whole number or 5.9 to 1dp.
Please help with math ASAP, will give brainliest!!

Answers
Answer:
Step-by-step explanation:
center (-1, -2) , trough point ( 6, 4)
equation of the circle
r² = (x-h)²+(y-k)², where (h, k) are the coordinate of a circle so h=-1, k=-2
r² =(x+1)²+(y+2)², but (x, y ) are coordinates for any point on the circle so x=6 and y= 4
r² =(6+1)²+(4+2)²
r²= 7² +6²
r²= 85
so the equation is
(x+1)²+(y+2)²= 85
to find the points on the circle substitute in the equation x and y
(-10+1)²+(0+2)²= 85 ; 85=85 true
so the pint on the circle is (-10, 0)
Use the Trapezoidal Rule, the Midpoint Rule, and Simpson's Rule to approximate the given integral with the specified value of n. (Round your answers to six decimal places.)
Answers
Trapezoidal value will be = - 1392.087124
Midpoint value will be = -1744.434609
Simpson value will be = - 1624.985447
What is Trapezoidal?A method for estimating the definite integral is the trapezoidal rule. displaystyle 'int _'a'b'f'(x), dx. The area of the region that roughly fits the shape of a trapezoid under the graph of the function f(x) is how the trapezoidal rule operates.
According to the given information:The subintervals have a length of 12/8, or 1.5, because the interval is 12.
let,
f(x) = sin(x)x³
Trapezoidal value will be:
\(\begin{aligned}&\int_{0}^{12} x^{3} \sin (x) d x \approx \\&0.75(f(0)+2 f(1.5)+2 f(3)+2 f(4.5)+2 f(6)+2 f(7.5)+2 f(9)+2 f(10.5)+f(12))\end{aligned}\)
= - 1392.087124
Midpoint value will be:
\(\begin{aligned}&\int_{0}^{12} x^{3} \sin (x) d x \approx \\&1.5 *(f(0.75)+f(2.25)+f(3.75)+f(5.25)+f(6.75)+f(8.25)+f(9.75)+f(11.25))\end{aligned}\)
= -1744.434609
Simpson value will be :
\(\begin{aligned}&\int_{0}^{12} x^{3} \sin (x) d x \approx \\&0.25(f(0)+4 f(0.75)+2 f(1.5)+4 f(2.25)+2 f(3)+4 f(3.75)+2 f(4.5)+4 f(5.25)+ \\&2 f(6)+4 f(6.75)+2 f(7.5)+4 f(8.25)+2 f(9)+4 f(9.75)+2 f(10.5)+4 f(11.25)+\end{aligned}\)
= - 1624.985447
Trapezoidal value will be = - 1392.087124
Midpoint value will be = -1744.434609
Simpson value will be = - 1624.985447
To know more about Trapezoidal rule visit:
https://brainly.com/question/17218343
#SPJ4
I understand that the question you are looking for is:
Use the Trapezoidal Rule, the Midpoint Rule, and Simpson's Rule to approximate the given integral with the specified value of n. (Round your answers to six decimal places.)12integral.gif0x3 sin(x) dx, n = 8
(a) the Trapezoidal Rule
(b) the Midpoint Rule
(c) Simpson's Rule
the game of american roulette involves spinning a wheel with 38 slots: 18 red, 18 black, and 2 green. a ball is spun onto the wheel and will eventually land in a slot, where each slot has an equal chance of capturing the ball. gamblers can place bets on red or black. if the ball lands on their color, they double their money. if it lands on another color, they lose their money. suppose you bet $3 on red. what's the expected value and standard deviation of your winnings? (round your answers to four decimal places.)
Answers
The expected value (EV) of betting $3 on red is -$0.16
The standard deviation (SD) of betting $3 on red is 2.995
What is the expected value of the bet?The expected value of the bet is calculated as follows:
there are 18 red slots out of 38 total, so the probability of winning a bet on red is 18/38, or 0.4737.
The probability of losing the bet is 1 - 0.4737, or 0.5263.
If the ball lands on red, the player wins $3, and if it lands on black or green, the player loses $3.
The expected value (EV) f betting $3 on red is:
EV = (probability of winning * amount won) + (probability of losing * amount lost)
EV = (0.4737 * $3) + (0.5263 * -$3)
EV = $1.42 - $1.58
EV = -$0.16
The standard deviation (SD) of betting $3 on red is:
SD = √[(probability of winning * (amount won - EV)²) + (probability of losing * (amount lost - EV)²)]
SD = √[(0.4737 * ($3 - (-$0.16))²) + (0.5263 * (-$3 - (-$0.16))²]
SD = √[(0.4737 * $9.98) + (0.5263 * $8.06)]
SD = √[$4.728 + $4.245]
SD = √($8.973)
SD = $2.995
Learn more about standard deviation at: https://brainly.com/question/475676
#SPJ1
Pls help me with this answer

Answers
And angle which would be 90 degrees
Do 52+90 =142
180-142=38
Then you’d do 44+38=82
180-82=98
(This is because angles on straight line add up to 180)
ANSWER = 98
A rectangular building ha a bae that i 255ft long, 255 feet wide, and the building i 42 ft tall. Find the unit for the volume of the building
Answers
The volume of the rectangular building is 2,731,050 feet³ depending on the given height, base and width.
The volume of the building will be calculated by the formula -
Volume = length × breadth × height
Thus, keeping the value of each component of building in the formula to find the volume of the building.
Volume of building = 255 × 255 × 42
Performing multiplication on Right Hand Side of the equation to find the value of volume
Volume of building = 2,731,050 feet³
Therefore, the volume of the building is 2,731,050 feet³.
Learn more about volume -
https://brainly.com/question/463363
#SPJ4
If Antonio has six white Soxs, two black Sox's, and four gray socks In his drawer then if he randomly chooses a sock from the drawer, what is the probability he will choose a gray sock?
Answers
Answer:
1/3
Step-by-step explanation:
What, so he doesn't have the Red Sox?
Jkjk, so anyway let's get back to the problem.
There is a total of 12 socks.
There are 4 gray socks.
4/12=1/3
1/3 probability
when solving a system of equations that includes one linear equation and one quadratic equation, how many solutions can be found?
Answers
A system of equations with one linear equation and one quadratic equation has "zero or one or two" solutions.
How to solve a system of equations that includes one linear equation and one quadratic equation?Consider a system of equations with one linear equation and one quadratic equation as
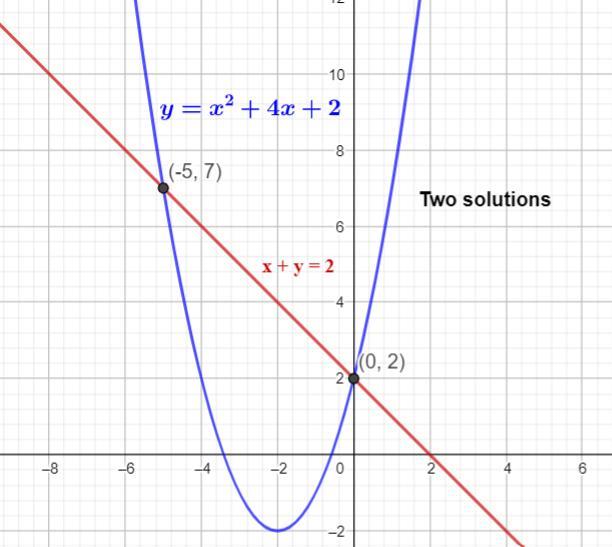
Case (1): y = x² + 4x + 2 ...(1)
and x + y = 2 ...(2)
By the substitution method:
from (2), y = 2 - x; Substituting in (1)
⇒ 2 - x = x² + 4x + 2
⇒ x² + 4x + 2 + x - 2 = 0
⇒ x² + 5x = 0
⇒ x(x + 5) = 0
∴ x = 0 and x = -5
If x = 0, then y = 2 - 0 = 2
If x = -5, then y = 2 + 5 = 7
So, the system has two solutions at (0, 2) and (-5, 7).
Case (2): y = x² + 4x + 2 ...(1)
and x - y = 2 ...(2)
By the substitution method:
from (2), y = x - 2; Substituting in (1)
⇒ x - 2 = x² + 4x + 2
⇒ x² + 4x + 2 + 2 - x = 0
⇒ x² + 3x + 4 = 0
we know that b² - 4ac will decide the nature of roots.
So, (3)² - 4(1)(4) = 9 - 16 = -7 < 0
Since the determinant is less than 0, the roots are imaginary. Hence the system has no solution. That means the line and the parabola do not meet.
Case (3): y = x² + 4x + 2 ...(1)
and y = x - 1/4 ...(2)
Substituting (2) in (1), we get
⇒ x - 1/4 = x² + 4x + 2
⇒ x² + 4x + 2 - x + 1/4 = 0
⇒ x² + 3x + 9/4 = 0
⇒ 4x² + 12x + 9 = 0
⇒ (2x + 3)² = 0
⇒ 2x + 3 = 0
∴ x = -3/2
If x = -3/2 then y = -3/4 - 1/4 = -7/4
So, the system has one solution at (-3/2, -7/4).
Therefore, the given type of system has "zero or one or two" solutions.
Learn more about the system of equations here:
brainly.com/question/2376175
#SPJ1


1. 5 2 1 4 0 0 7 2 8 1 m m 7 m 5 m A. 3656 D. 2739 B. 1841 E.5418 C. 3556
Answers
Given statement solution is :- We cannot find the missing value from the given options (3656, 2739, 1841, 5418, or 3556).
The given sequence is: 5 2 1 4 0 0 7 2 8 1 m m 7 m 5 m A.
To find the missing value, let's analyze the pattern in the sequence. We can observe the following pattern:
The first number, 5, is the sum of the second and third numbers (2 + 1).
The fourth number, 4, is the sum of the fifth and sixth numbers (0 + 0).
The seventh number, 7, is the sum of the eighth and ninth numbers (2 + 8).
The tenth number, 1, is the sum of the eleventh and twelfth numbers (m + m).
The thirteenth number, 7, is the sum of the fourteenth and fifteenth numbers (m + 5).
The sixteenth number, m, is the sum of the seventeenth and eighteenth numbers (m + A).
Based on this pattern, we can deduce that the missing values are 5 and A.
Now, let's calculate the missing value:
m + A = 5
To find a specific value for m and A, we need more information or equations. Without any additional information, we cannot determine the exact values of m and A. Therefore, we cannot find the missing value from the given options (3656, 2739, 1841, 5418, or 3556).
For such more questions on Missing value: Indeterminable.
https://brainly.com/question/30389332
#SPJ8
a. (-2,4) (-1,1) (-3,-1) (-5,2)
b. (2,4) (1,1) (3,1) (5,2)
c. (4,2) (1,1) (1,3) (2,5)
d. (4,-2) (1,-1) (-1,-3) (2,-5)

Answers
S'(4, -2) and T'(1, -1) and U'(-1, -3) and V'(2, -5)
Step-by-step explanation:\(Find\ the\ coordinates\ of\ the\ point\ after\ reflected\ in\ the\ line\ of\ symmetry:\\ \downarrow\\ S'(-4,-2)\ and\ T'(1,-1)\ and\ U'(-1,-3)\ and\ V'(2,-5)\)
I hope this helps you
:)
HELP ASAP
High-quality goods and services are made available to consumers because of producers __________.
A.hold self-interests
B.would like to compete
C.look for subsidies
D.specialize in production
Please select the best answer from the choices provided
A
B
C
D
Answers
Answer:
I think it’s D.
Step-by-step explanation:
HELLO PLWASE HELP PLEASE PLEASE

Answers
Answer:
just count the square from y or x axis then multply divide and wola theres the answr
Step-by-step explanation:
The Riemann zeta function for real numbers is defined for all x for which the series below converges. Find the domain of the function. (Enter your answer using interval notation.)
(x)=infinite to n=1 (n^-x)
Answers
In interval notation, the domain is (1, ∞).
The Riemann zeta function for real numbers is defined as ζ(x) = ∑n=1 to ∞ (n^-x) for all x for which the series converges.
To find the domain of the function, we need to determine for which values of x the series converges.
Using the p-series test, we know that the series ∑n=1 to ∞ (n^-x) converges if x > 1. Therefore, the domain of the Riemann zeta function is x > 1.
In interval notation, the domain is (1, ∞).
To know more about the Riemann zeta function visit:
https://brainly.in/question/46964748
#SPJ11