Triangle ABC is a right triangle
The length of BC is 5 units.
The area of ABC is
square units.
10
Answers
Answer:
the height of the triangle is 4
Step-by-step explanation:
2a/b
2(10/5)
2*2
=4
Answer:
The answer is 50.
Step-by-step explanation:
Related Questions
Consider the line y=x+9.
What is the slope of a line parallel to this line?
What is the slope of a line perpendicular to this line?
Answers
Answer:
parallel: 1, perpendicular: -1
Step-by-step explanation:
slope of a parallel line is the same
slope of a perpendicular line is a negative recipricol
slope of y=x+9 is 1
parallel: 1
perpendicular: -1
Please look at the photo. Thank you!

Answers
The equations of the composite functions are (h o h)(x) = (x² + 3)² + 3 and (f o f)(x) = x
How to calculate the composite functionsFrom the question, we have the following equations that can be used in our computation:
h(x) = x² + 3
f(x) = 3/4x
From the above, we have
(h o h)(x) = h(h(x))
So, we have
(h o h)(x) = (x² + 3)² + 3
Also, we have
(f o f)(x) = 3/[4(3/4x)]
Evaluate
(f o f)(x) = x
Hence, the composite functions are (h o h)(x) = (x² + 3)² + 3 and (f o f)(x) = x
Read more about composite functions at
brainly.com/question/33401202
#SPJ1
What is −1/2a+2/5+5/6a−1/10 written in simplest form?
Answers
Answer:
simple
Step-by-step explanation:
Can you tell which 3-D shape this would make?

Answers
Answer:
the answer is A
Step-by-step explanation:
you can see the image dont have stand. so it cannot be 3d. 3d need right left up down to fullfil the box
Dosen"t fold to make a 3D shape.
What is 3D shape?3D shapes exist in forms with three dimensions, such as width, height, and depth. An example of a 3D shape exists as a prism or a sphere. 3D shapes exist as multidimensional and can be physically held.
A 2D shape includes two dimensions- length and breadth. A 3D shape contains three dimensions- length, breadth, and height.
The figure doesn't fold to make a 3-D shape as it doesn't have all the specified number of sides for any given shapes.
To learn more about 3D shape refer to:
https://brainly.com/question/25965491
#SPJ2
Which of the following is the graph of the function shown below?
W.
X.
Y.
Z.
A.
X
B.
Y
C.
W
Answers
Answer:
Cannot be drawn directly.
Step-by-step explanation:
The graph of every function w = f (x, y, z) will be a surface in R 4, though it can't be drawn directly; however, slicing horizontally by w = c produces relations c = f (x, y, z) in x, y, and z whose graphs will be surfaces in 3-space which can be drawn. Therefore, the graph of the function shown above cannot be drawn directly.
I drove 527 miles and used 24 gallons of gas.
Answers
Answer:
21.9
Step-by-step explanation:
assuming you are asking about how much miles per gallon you got 21.9 would be the answer you just simply divide 527 by 24
Answer:
21.96 miles per gallon
Step-by-step explanation:
Find the slope of the line that passes through (1, 14) and (4,9)
Which two numbers in the points represent x values? Select both in the
list.
Answers
In any coordinate pair, the first number is the x-value and the second number is the y-value.
To find the slope, simply take the difference of the y values and divide by the difference in the x values: (14-9)/(1-4) is equal to -5/3.
The slope of the line that passes through (1, 14) and (4,9) is -5/3.
It is find the slope of the line.
what is slope?The slope of any line, ray, or line segment is the ratio of the vertical to the horizontal distance between any two points on it (“slope equals rise over run”).
The slope is always calculated from the rise divided by the run. Typically, the equation is presented as:
m = Rise/Run
If you have two points, the points should be \(P_{1} (x_{1} ,y_{1} )\) and \(P_{2} (x_{2} ,y_{2} )\) So, the equation would be:
\(m=\frac{y_{2}-y_{1} }{x_{2}-x_{1} }\)
In any coordinate pair, the first number is the x-value and the second number is the y-value.
The difference of the y values and divide by the difference in the x values:
m=(14-9)/(1-4) is equal to -5/3.
The slope of the line that passes through (1, 14) and (4,9) is -5/3.
Learn more about slope here:
https://brainly.com/question/17114095
#SPJ5
What are the intercepts of the following
equation?
3x - 6y = -12

Answers
Answer:
x-intercept will be: (-4, 0)y-intercept will be: (0, 2)Step-by-step explanation:
Given the equation
\(3x\:-\:6y\:=\:-12\)
We know that x-intercept is obtained when we put y = 0,
so
\(3x\:-\:6y\:=\:-12\)
3x - 6(0) = -12
3x = -12
x = -4
Therefore, x-intercept will be: (-4, 0)
We know that y-intercept is obtained when we put x = 0,
\(3x\:-\:6y\:=\:-12\)
3(0) - 6y = -12
-6y = -12
y = 2
Therefore, y-intercept will be: (0, 2)
Last year Lenny had an annual earned income of 58,475 he also had passive income of 1,255 and capital gains of 2,350 what was lennys total gross income for the year
Answers
58,475+1,255+2,350 =62,080
Answer:
The answer is D, $62,080
What type of matter is pure gold
a heterogenous mixture
a homogenous mixture
a compound
an element
Answers
Answer:
an element
Step-by-step explanation:
.
Step-by-step explanation:
a ) Heterogenous Mixture
Is the answer
PLEASE MARK AS BRAINLIEST ANSWER
a pizzeria had 4 cans of tomato sauce how many pizzas could they make with the cans if each pizza took one fourth of a can
Answers
Answer:
16 pizzas.
Step-by-step explanation:
That is 4 divided by 1/4
= 4 * 4/1
= 16.
Answer:
16
Step-by-step explanation:
There are 4 pizzas per can and you have 4 cans.
4 x 4 = 16
Hallar la cantidad de permutaciones diferentes de 7 letras que se pueden formar con las letras de la
palabra COBATAB
a) Si se deja fija la letra C.
b) Si se deja fija la última letra.
Answers
a. The number of permutations possible is 6!, which is equal to 720.
b. The number of different permutations is 2 × 6!, which is equal to 1440.
What are permutations?
An arrangement of items in a specific sequence is referred to as a permutation. Here, the components of sets are arranged in a linear or sequential manner.
a) If the letter C is left fixed, then we have 6 letters left to form the permutation. The number of permutations possible is 6!, which is equal to 720.
b) If the last letter is left fixed, then we have 6 letters left to form the permutation. The number of permutations possible is also 6!, but we need to consider that each permutation can be written in two different ways depending on which letter is fixed at the end. Therefore, the number of different permutations is 2 × 6!, which is equal to 1440.
Learn more about permutations on:
https://brainly.com/question/1216161
#SPJ1
The correct question is:
Find the number of different permutations of 7 letters that can be formed with the letters of the
word COBATAB
(a) If letter C is left fixed.
b) If the last letter is left fixed.
There are six pizzas there are 36 players on the team. If each member has one slice and each pizza has eight slices how much pizza in fraction form will be left over.
Answers
There will be 12 slices of pizza left over, which can be expressed as 3/2 or 1 1/2 slices in fraction form.
To find out how much pizza will be left over, we need to calculate the total number of slices available and subtract the number of slices consumed by the players.
Given that there are six pizzas and each pizza has eight slices, the total number of slices available is 6 pizzas * 8 slices/pizza = 48 slices.
Since there are 36 players on the team, and each player has one slice, the total number of slices consumed is 36 slices.
To determine the remaining slices, we subtract the consumed slices from the total available slices: 48 slices - 36 slices = 12 slices.
Therefore, there will be 12 slices of pizza left over.
To express this as a fraction, we can write it as 12/1, which simplifies to 12. This means there will be 12 whole slices of pizza left over.
If you would like to express it as a fraction in its simplest form, you can write it as 12/8. By dividing both the numerator and denominator by their greatest common divisor, which is 4, we get 3/2. So, in fraction form, there will be 3/2 or 1 1/2 slices of pizza left over.
for more questions on fraction
https://brainly.com/question/78672
#SPJ8
can someone please help

Answers
Answer:
The measure of CD is 46
Step-by-step explanation:
From the midpoint theorem, we have,
FG = (1/2)CD
so,
\(13+5x=(1/2)(-3x+52)\\So,\\2(13+5x)=-3x+52\\26+10x=-3x+52\\13x=52-26\\13x=26\\x=26/13\\x=2\)
Now,
\(CD = -3x+52\\since \ x=2\\we \ get\\CD=-3(2) +52\\CD=-6+52\\CD=46\)
Two six-sided dice are rolled. Using the sample space for rolling two dice shown in the figure below, find the probability that the sum of the dice is either 4 or 7. Give your answer as a reduced fraction.
Answers
Answer:
Step-by-step explanation:
There are 36 ways 2 dice can be thrown. Sometimes colors are used to tell the difference between the dice.
36 comes from 6*6
Suppose you have 2 dice 1 blue and the other white
Blue White
1 1
2
3
4
5
6
There's 6 ways that have been thrown. Then you go to the blue dice being 2. You get six more. Then 3 gives you six more 4 gives you another six. and so on. The whole procedure adds to 36
you can throw a four 3 ways
Blue white
1 3
3 1
2 2
You can throw 7 six ways
Blue white
1 6
6 1
2 5
5 2
3 4
4 3
So of the 36 ways to throw the dice 9 will successful. (6 + 3)
Answer: 9/36 = 1/4 times you will be successful
Find the value of x.

Answers
Answer:
These x-values are known as the “roots” or “zeros” of the quadratic. To find these roots, we simply set the quadratic equal to zero and solve for x
Step-by-step explanation:
The difference of three times a number and eight is two more than the number.
Answers
Answer:
The number is 5.
Step-by-step explanation:
Let x be the number.
\(3x - 8 = x + 2\)
\(2x = 10\)
\(x = 5\)
n a certain class of students, there are 20 boys and 15 girls. If the teacher calls upon a student to answer a question, what is the probability that the student will be a boy?
Answers
Answer:
57%
Step-by-step explanation:
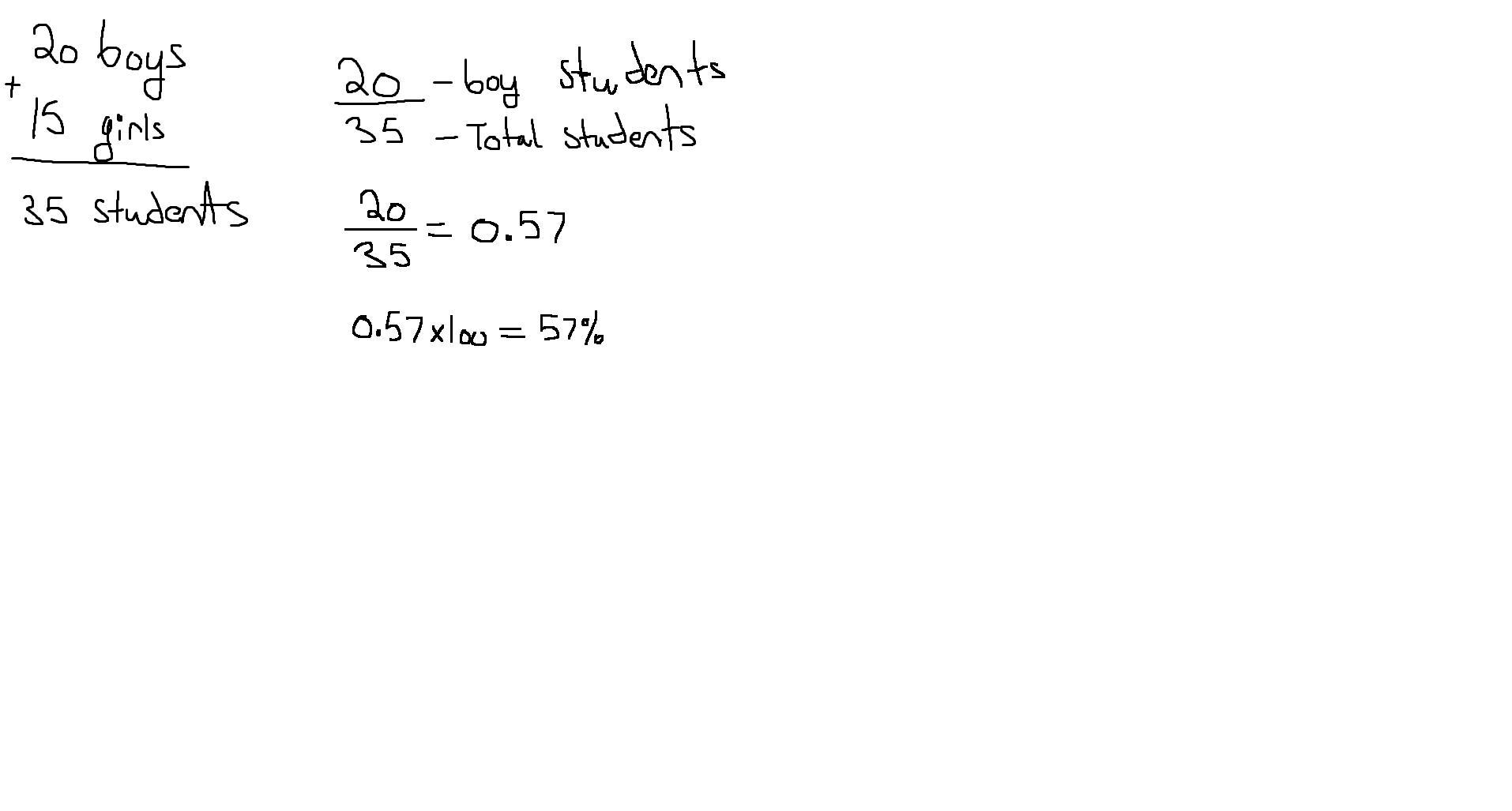
Identify the number line that correctly displays the solution x ≥ 3.




Answers
The correct number line that displays the solution `x ≥ 3` would be:
<------|------|------|------|------|------|------|------|------|------|------|------|------|------|------|------|------|------|------|------|------>
-10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10
●------------------------------------------------>
The solution `x ≥ 3` is an inequality that means x is greater than or equal to 3. To graph this inequality on the number line, we mark the point representing the value 3 with a closed circle on the number line and draw an arrow pointing to the right to indicate that all values greater than or equal to 3 satisfy the inequality.
The closed circle at 3 indicates that 3 is included in the solution set, and the arrow to the right indicates that all values greater than 3 also satisfy the inequality. Therefore, any value of x that is equal to or greater than 3 would be considered a solution to the inequality `x ≥ 3`.
It is important to note that if the inequality was `x > 3` (without the equal sign), the closed circle at 3 would be changed to an open circle, indicating that 3 is not included in the solution set, and only values greater than 3 would be considered solutions. In conclusion, the number line provided above correctly displays the solution `x ≥ 3`.
For such more questions on number line
https://brainly.com/question/24644930
#SPJ8
Kelvin, Celsius, and Fahrenheit are three types of
scales.
Answers
Answer:
Temperature
Step-by-step explanation:
the internet does wonders
Kelvin, Celsius, and Fahrenheit are three types of scales used to measure temperature. They all are related with each other as they all measure same thing, which is 'temperature'.
How are Kelvin, Celsius, and Fahrenheit related?We have got an equation that can relate these three units of measurement of temperature, as given below:
\(\dfrac{C}{5} = \dfrac{F - 32}{9} = \dfrac{K - 273}{5}\)
where C represents the measurement of a fixed temperature in Celsius, F represents the measurement of that same intensity temperature in Fahrenheit, and K represents the measurement of equally intense temperature in Kelvin.
Thus, Kelvin, Celsius, and Fahrenheit are three types of scales used to measure temperature. They all are related with each other as they all measure same thing, which is 'temperature'.
Learn more about temperature scale here:
https://brainly.com/question/2919967
#SPJ2
Write a sine function with an amplitude of 5, a period of
Pi/8,and a midline at y = 7.
f(x) = 4sin(8x) + 5
f(x) = 5sin(16)+7
f(x) = 5sin(16x) + 4
f(x) = 4sin(8x) + 7
Answers
Answer:
\(\textsf{B)} \quad f(x) = 5 \sin (16x) + 7}\)
Step-by-step explanation:
The sine function is periodic, meaning it repeats forever.
Standard form of a sine function\(\boxed{f(x) = A \sin (B(x + C)) + D}\)
where:
A is the amplitude (height from the midline to the peak).2π/B is the period (horizontal distance between consecutive peaks).C is the phase shift (horizontal shift - positive is to the left).D is the vertical shift (y = D is the midline).Given values:
Amplitude, A = 5Period, 2π/B = π/8Phase shift, C = 0Vertical shift, D = 7Calculate the value of B:
\(\dfrac{2\pi}{B}=\dfrac{\pi}{8}\implies 16\pi=B\pi\implies B=16\)
Substitute the values of A, B C and D into the standard formula:
\(f(x) = 5 \sin (16(x + 0)) + 7\)
\(f(x) = 5 \sin (16x) + 7\)
Therefore, the sine function with an amplitude of 5, a period of π/8, and a midline at y = 7 is:
\(\Large\boxed{\boxed{f(x) = 5 \sin (16x) + 7}}\)

Need help with this question please !!!
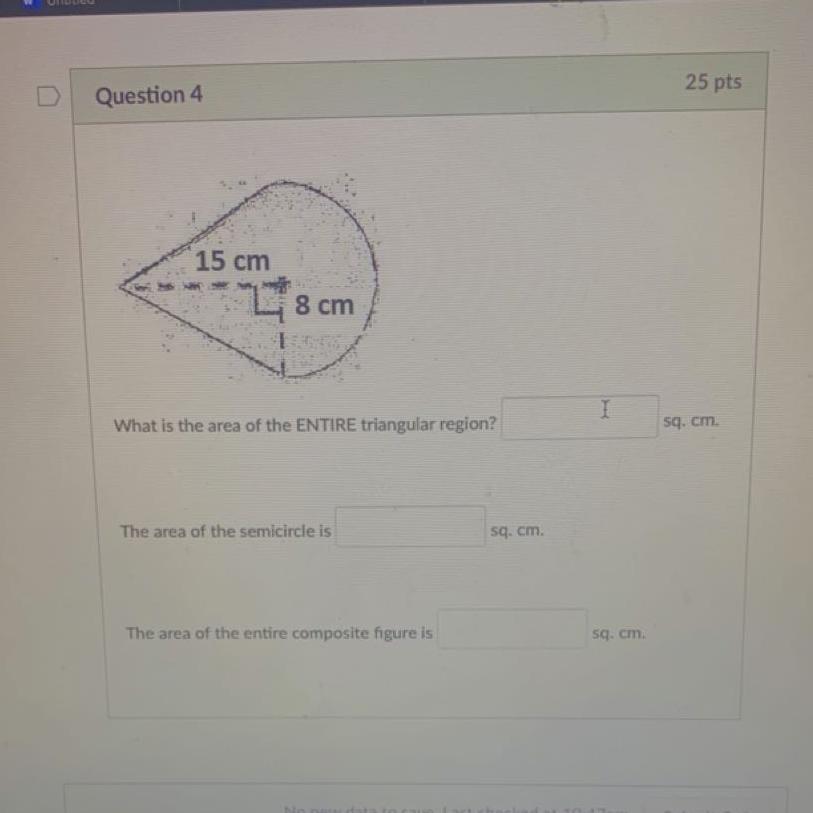
Answers
Answer: 27
Step-by-step explanation:
Factor the expression below. 9x^2-1 A. (3x - 1)(3x - 1) B. (3x - 1)(3x + 1) C. (x - 1)(9x - 1) D. (x - 1)(9x + 1)
Answers
Answer:
(3x + 1) • (3x - 1)
Step-by-step explanation:
Step by Step Solution
More Icon
STEP
1
:
Equation at the end of step 1
3\({}^{2}\)x\({}^{2}\) - 1
STEP
2
:
Trying to factor as a Difference of Squares:
2.1 Factoring: 9x\({}^{2}\)-1
Theory : A difference of two perfect squares, A\({}^{2}\) - B\({}^{2}\) can be factored into (A+B) • (A-B)
Proof : (A+B) • (A-B) =
A\({}^{2}\) - AB + BA - B2 =
A\({}^{2} \)- AB + AB - B2 =
A\({}^{2}\) - B2
Note : AB = BA is the commutative property of multiplication.
Note : - AB + AB equals zero and is therefore eliminated from the expression.
Check : 9 is the square of 3
Check : 1 is the square of 1
Check : x\({}^{2}\) is the square of x1
Factorization is : (3x + 1) • (3x - 1)
Final result :
(3x + 1) • (3x - 1)
In a survey of 259 professional athletes, it was found that 110 of them owned a convertible, 91 of
them owned a giant screen TV, and 120 owned a sporting goods store. 15 owned a convertible and a
store, 43 owned a TV and a store, and 44 owned a covertible and a TV. 9 owned all three items.
1. How many athletes did not own any of the three items?
2. How many owned a covertible and a TV, but not a store?
3. How many athletes owned a convertible or a TV?
4. How many athletes owned exactly one type of item in the survey?
5. How many athletes owned at least one type of item in the survey?
6. How many owned a TV or a store, but not a convertible?
Answers
1. Number of athletes did not own any of the three items = 259 - 228
= 31.
2. Number of athletes own a convertible and a TV but not a store = 44 - 9
= 35.
3. Number of athletes own a convertible or a TV = 110 + 91 - 44
= 157.
4. Number of athletes owned exactly one type of item = 60 + 13 + 71 = 144.
5. Number of athletes owned at least one type of item = 259 - 31
= 228
6. Number of athletes own a TV or a store, but not a convertible = 13 + 34 +71
= 118.
The number of athletes did not own any of the three items need to subtract the number of athletes who own at least one item from the total number of athletes surveyed.
Total number of athletes surveyed = 259
Number of athletes own at least one item = 110 + 91 + 120 - 15 - 43 - 44 + 9 = 228
Number of athletes who did not own any of the three items = 259 - 228 = 31.
The number of athletes who owned a convertible and a TV but not a store need to subtract the number of athletes who own all three items from the number of athletes who own a convertible and a TV.
Number of athletes who own a convertible and a TV = 44
Number of athletes who own all three items = 9
Number of athletes who own a convertible and a TV but not a store = 44 - 9 = 35
The number of athletes who owned a convertible, or a TV need to add the number of athletes who own a convertible to the number of athletes who own a TV and then subtract the number of athletes own both a convertible and a TV.
Number of athletes who own a convertible or a TV = 110 + 91 - 44
= 157.
The number of athletes owned exactly one type of item need to add up the number of athletes who own a convertible only the number of athletes own a TV only and the number of athletes who own a store only.
Number of athletes own a convertible only = 110 - 15 - 9 = 86
Number of athletes own a TV only = 91 - 44 - 9 = 38
Number of athletes own a store only = 120 - 15 - 43 - 9 = 53
Number of athletes owned exactly one type of item = 60 + 13 + 71 = 144.
The number of athletes who owned at least one type of item can use the result from part (1).
Number of athletes who owned at least one type of item = 259 - 31
= 228
The number of athletes who owned a TV or a store but not a convertible need to subtract the number of athletes who own all three items, and the number of athletes own a convertible and a TV from the number of athletes own a TV or a store.
Number of athletes own a TV or a store = 91 + 120 - 43 - 9 = 159
Number of athletes own a TV or a store not a convertible = 13 + 34 +71
= 118.
For similar questions on athletes
https://brainly.com/question/25631156
#SPJ11
Given the function f(x) = 0.5|x - 41-3, for what values of x is f(x) = 7?
x = -24, x = 16
x= -16, x = 24
x=-1, x = 9
x = 1, x = -9
Answers
The values of x for which f(x) = 7 are x = 61 and x = 21.
To find the values of x for which f(x) = 7, we can set up the equation and solve for x.
The given function is f(x) = 0.5|x - 41| - 3.
Setting f(x) equal to 7, we have:
0.5|x - 41| - 3 = 7.
First, let's isolate the absolute value term:
0.5|x - 41| = 7 + 3.
0.5|x - 41| = 10.
To remove the absolute value, we can consider two cases:
Case: (x - 41) is positive or zero:
0.5(x - 41) = 10.
Multiplying both sides by 2 to get rid of the fraction:
x - 41 = 20.
Adding 41 to both sides:
x = 61.
So x = 61 is a solution for this case.
Case: (x - 41) is negative:
0.5(-x + 41) = 10.
Multiplying both sides by 2:
-x + 41 = 20.
Subtracting 41 from both sides:
-x = -21.
Multiplying both sides by -1 to solve for x:
x = 21.
So x = 21 is a solution for this case.
Therefore, the values of x for which f(x) = 7 are x = 61 and x = 21.
for such more question on values
https://brainly.com/question/11546044
#SPJ8
Picture of coordinates (5,4) (3,4)
On a Cartesian plan
Answers
Both the coordinate points are plotted on the graph. The cartesian graph is attached with the answer.
What are coordinates?Coordinates are numbers which determine the position of a point or a shape in a particular space (a map or a graph). In the cartesian coordinate system, the coordinates are of the form (x, y).Other coordinate systems are : cylindrical and spherical coordinate systemGiven are the two coordinates to be plotted on a Cartesian plan -
(5, 4) , (3, 4).
The two given coordinate points are (5, 4) , (3, 4).
Refer to the graph attached. It shows both the points plotted.
Therefore, both the coordinate points are plotted on the cartesian graph.
To solve more questions on coordinates plotting and graphs, visit the link below -
https://brainly.com/question/24952385
#SPJ1

Which one is the best prediction! Please and no link answer :(

Answers
Answer:
\(Prediction = 35\)
Step-by-step explanation:
Given
The attached table
Required
Expected number of Daffodil when N = 150
First, we calculate the probability of having a Daffodil.
\(Pr = \frac{Daffodil}{Total}\)
This gives:
\(Pr = \frac{14}{14+10+24+12}\)
\(Pr = \frac{14}{60}\)
Simplify
\(Pr = \frac{7}{30}\)
When there are 150 flowers, the prediction of Daffodils is:
\(Prediction = Pr * N\)
\(Prediction = \frac{7}{30} * 150\)
\(Prediction = 7*5\)
\(Prediction = 35\)
A snowplow removes three fourths of the snow each time that it goes down a road. If a road starts with 24
inches of snow on it, determine how many times the road would need to be plowed in order for there to be less
than 1/2 inch of snow left on the road.
Answers
After 94/3 times, the snow left on the road will be less than 1/2 inch if the snowplow removes three-fourths of the snow each time.
What is a fraction?Fraction number consists of two parts, one is the top of the fraction number which is called the numerator and the second is the bottom of the fraction number which is called the denominator.
Let's suppose the after x times the snow left on the road is less than 1/2 inches
Each time, the snowplow removes 3/4 of the snow.
Then according to the problem:
24 - 3x/4 = 1/2
3x/4 = 24 - 1/2
3x/4 = 47/2
3x/2 = 47
x = 47(2)/3 = 94/3 times
Thus, after 94/3 times, the snow left on the road will be less than 1/2 inch if the snowplow removes three-fourths of the snow each time.
Learn more about the fraction here:
brainly.com/question/1301963
#SPJ2
I need to know how can I solve this, I really don’t know how to do it

Answers
The sample space for rolling two number cubes is shown below
1 2 3 4 5 6
1 1,1 1,2 1,3 1,4 1,5 1,6
2 2,1 2,2 2,3 2,4 2,5 2,6
3 3,1 3,2 3,3 3,4 3,5 3,6
4 4,1 4,2 4,3 4,4 4,5 4,6
5 5,1 5,2 5,3 5,4 5,5 5,6
6 6,1 6,2 6,3 6,4 6,5 6,6
Looking at the sample space, the outcomes where the sum is greater than 8 are
3, 6
4, 5
4, 6
5, 4
5, 5
5, 6
6, 3
6, 4
6, 5
6, 6
Thus, the correct answer is the last option
Which equation represents the slope-intercept form of the line below?
y-intercept = (0,-6)
slope = -5
O A. y = -6x + 5
O B. y = -5x - 6
O C. y = -5x + 6
D. y = -6x-5
Answers
Hi there!
»»————- ★ ————-««
I believe your answer is:
Option B: \(y=-5x-6\)
»»————- ★ ————-««
Here’s why:
Recall that the slope intercept form of a equation for a line is:⸻⸻⸻⸻
\(\boxed{\text{Slope-Intercept Form:}}\\\\------------\\y=mx+b\\\\\boxed{\text{\underline{Key}}}\\\\\rightarrow\text{m - slope}\\\\\rightarrow\text{b - y-intercept}\)
⸻⸻⸻⸻
We are given the information of:
The slope, which is -5.The y-intercept, which is (0, -6).⸻⸻⸻⸻
\(\boxed{\text{Replace The Variables with The Appropriate Values:}}\\\\y=mx+b\\\\\rightarrow\text{-5 would replace 'm', -6 would replace 'b'.}\\\\\text{\underline{Therefore:}}\\\\y=mx+b\rightarrow\boxed{y=-5x-6}\)
⸻⸻⸻⸻
Option B should be the correct answer.
»»————- ★ ————-««
Hope this helps you. I apologize if it’s incorrect.