Two balloons, Balloon A and Balloon B have a total volume of gallons. Balloon A has a greater volume than Balloon B. The difference in their volumes is a gallon. What is the volume of each balloon?
Answers
Answer:
A=2 B=1
Step-by-step explanation:
Related Questions
Does the sum of angles of any triangle will always equal 180 degrees?
Answers
Answer:
yes the sum of any triangle is 180°
Step-by-step explanation:
I hope it's helps you
Hi can u plzz help me with these thank you!!!
1. If the diameter of a circular object is 10 feet. Find the radius and the circumference. Use 3.14 for π.
2. Find the perimeter of the window. R = 4ft
Answers
Answer:
1.
\(Radius = 5ft\)
\(Circumference = 31.4\ ft\)
2.
\(Perimeter = 25.12\ ft\)
Step-by-step explanation:
Solving (1):
Given
\(Diameter = 10ft\)
Required
Determine the radius and circumference
Radius is calculated as follows:
\(Radius = \frac{1}{2} * Diameter\)
\(Radius = \frac{1}{2} * 10ft\)
\(Radius = 5ft\)
The circumference is calculated using:
\(Circumference = 2 * \pi * Radius\)
\(Circumference = 2 * 3.14 * 5ft\)
\(Circumference = 31.4\ ft\)
Solving (2):
Given
\(R = 4ft\)
Assume that the window is circular, the perimeter is calculated as follows:
\(Perimeter = 2 * \pi * R\)
\(Perimeter = 2 * 3.14 * 4ft\)
\(Perimeter = 25.12\ ft\)
Mr. Edwards bought a 50-pound bag of flour for his bakery. It was equally divided among 6 days. How much flour was used per day?
Answers
Answer:
8 \(\frac{1}{3}\)
Step-by-step explanation:
50 ÷ 6 = 8.3333333333... Which simplify's (as a fraction) into 8 \(\frac{1}{3}\).
Each day 8.33 pounds of flour is used.
What is Unitary Method?The unitary technique involves first determining the value of a single unit, followed by the value of the necessary number of units.
For example, Let's say Ram spends 36 Rs. for a dozen (12) bananas.
12 bananas will set you back 36 Rs. 1 banana costs 36 x 12 = 3 Rupees.
As a result, one banana costs three rupees. Let's say we need to calculate the price of 15 bananas.
This may be done as follows: 15 bananas cost 3 rupees each; 15 units cost 45 rupees.
Given:
Mr. Edwards bought a 50-pound bag of flour for his bakery.
It was equally divided among 6 days.
So, According per day the flour will be used
= 50/6
= 25/3
= 8.33 pound
Hence, 8.33 pounds used per day.
Learn more about Unitary Method here:
https://brainly.com/question/22056199
#SPJ2
What are the roots of the quadratic equation below?
2x2 - 12x + 13 = 0

Answers
Answer:
D
Step-by-step explanation:
Quadratic formula: \(\frac{-b+-\sqrt{b^2-4ac} }{2a}\)
\(2x^2- 12x + 13 = 0\)
\(x=\frac{-(-12)+-\sqrt{(-12)^2-4(2)(13)} }{2(2)}\)
\(x=\frac{12+-\sqrt{144-104} }{4}\)
\(x=\frac{12+-\sqrt{40} }{4}\)
\(x=\frac{12+-2\sqrt{10}}{4}\)
\(x=\frac{6+-\sqrt{10}}{2}\)
I hope this helps!
In the parallelogram below, solve for x and y. (Give your answer as a decimal, when necessary)

Answers
Answer: x = 15, y = 12.5
Step-by-step explanation:
The sum of the three angle measures of a triangle equals 180ᴼ
Since these triangles are vertical, the measures are congruent.
45 + 60 = 105
180 - 105 = 75
So now we know that 5x = 75ᴼ and 6y = 75ᴼ.
To find x, divide 75 by 5
75 / 5 = 15
x = 15
To find y, divide 75 by 6
75 / 6 = 12.5
y = 12.5
Answer this .......... according to thererom of circleanswer only (a) part

Answers
Solution:
(a) In the given figure,
\(\angle ABO=x\)BD is the bisector of angle ABC, thus:
\(\angle ABD=\angle DBC\)So, write as follows:
(i)
\(\angle ABC=\angle ABD+\angle DBC\)\(\begin{gathered} \angle ABC=\angle ABD+\angle ABD \\ \angle ABC=2\angle ABD \\ \angle ABC=2\angle ABO \\ \angle ABC=2x \end{gathered}\)Therefore,
\(\operatorname{\angle}ABC=2x\)(ii)
OB=OA=OD radii of the same circle.
As OB=OA then in triangle AOB,
\(\angle ABO=\angle BAO=x\)BOD is a diameter of a circle. then by theorem of circle,
\(\angle BAD=90^{\circ}\)thus,
\(\angle OAD=\angle BAD-\angle OAB\)\(\angle OAD=90^{\circ}-x\)OA=OD , in the tringle AOD,
\(\angle OAD=\angle ODA=90^{\circ}-x\)In triangle AOD,
\(\angle AOD+\angle OAD+\angle ODA=180^{\circ}\)\(\begin{gathered} \angle AOD+90^{\circ}-x+90^{\circ}-x=180^{\circ} \\ \angle AOD+180^{\circ}-2x=180^{\circ} \\ \angle AOD=2x \end{gathered}\)Therefore,
\(\begin{equation*} \angle AOD=2x \end{equation*}\)(iii) By the theorem of circle, the angle formed at the center of the circle is twice the angle formed at the circumference of the circle with the same base.
\(\angle AOC=2\angle ABC\)\(\begin{gathered} \angle AOC=2\times2x \\ \angle AOC=4x \end{gathered}\)Therefore,
\(\operatorname{\angle}AOC=4x\)(iv)
OA=OD , thus tringle AOD is an isosceles triangle,
\(\angle OAD=\angle ODA=90^{\circ}-x\)\(\begin{gathered} \angle ADO=90^{\circ}-x \\ \angle ADB=90^{\circ}-x \end{gathered}\)Therefore,
\(\begin{equation*} \angle ADB=90^{\circ}-x \end{equation*}\)How many different sums of money can be made from 4coins of different denomination
Answers
Answer:
15 different sums----------------------
There are various combinations of coins.
1 coin:4 options2 coins:4C2 = 4!/(2!2!) = 6 options3 coins:4C3 = 4!/(3!1!) = 4 options4 coins: 1 optionIn total there are:
4 + 6 + 4 + 1 = 15 different sumsSolve the two simultaneous equations.
You must show all your working.
3t+2p=15.5
5t+4p=28.5
Answers
Answer:
Given equations are,
5x+2y=−2 (1)
3x−5y=17.4 (2)
Multiply equation (1) by 5 and equation (2) by 2, we get,
5(5x+2y)=5×−2
∴25x+10y=−10 (3)
2(3x−5y)=2×17.4
∴6x−10y=34.8 (4)
Adding equations (3) and (4), we get,
31x=24.8
∴x=
31
24.8
Put this value in equation (1), we get,
5(
31
24.8
)+2y=−2
∴
31
124
+2y=−2
∴2y=−2−
31
124
∴2y=
31
−186
∴y=
31
−93
Step-by-step explanation:
Which of these three expressions are equivalent? Show your work. 7(2 + 3x) - 3x 2(6x + 7) + 10x 4(3 + 3x) + 2(1 + 3x)
Answers
The equivalent expressions are:
7(2 + 3x) - 3x and 4(3 + 3x) + 2(1 + 3x)
What is an expression?An expression is a way of writing a statement with more than two variables or numbers with operations such as addition, subtraction, multiplication, and division.
Example: 2 + 3x + 4y = 7 is an expression.
We have,
a)
7(2 + 3x) - 3x
= 14 + 21x - 3x
= 14 + 18x _____(1)
b)
2(6x + 7) + 10x
= 12x + 14 + 10x
= 22x + 14 _____(2)
c)
4(3 + 3x) + 2(1 + 3x)
= 12 + 12x + 2 + 6x
= 14 + 18x ______(3)
From (1), (2), and (2).
7(2 + 3x) - 3x and 4(3 + 3x) + 2(1 + 3x) are equivalent.
Thus,
7(2 + 3x) - 3x and 4(3 + 3x) + 2(1 + 3x) are equivalent expression.
Learn more about expressions here:
https://brainly.com/question/3118662
#SPJ1
Consider these statements written in ordinary language:_______.
A. The speed of the car is proportional to the distance it has traveled.
B. The car is speeding up.
C. The car is slowing down.
D. The car always travels the same distance in the same time interval.
E. We are driving backwards.
F. Our acceleration is decreasing. Denoting by s(t) the distance covered by the car at time t, and letting k denote a constant, match these statements with the following mathematical statements by entering the letters A through F on the appropriate boxes:_______.
s ′′ <0. s″<0.
s ′ s′ is constant
s ′ <0 s′<0
s ′′′ <0 s‴<0
s ′′ >0 s″>0
s ′ =ks s′=ks
Answers
Correct question is;
Consider these statements written in ordinary language:
A The speed of the car is proportional to the distance it has traveled.
B The car is speeding up.
C The car is slowing down.
D The car always travels the same distance in the same time interval.
E We are driving backwards.
F Our acceleration is decreasing. Denoting by s(t) the distance covered by the car at time t, and letting k denote a constant, match these statements with the following mathematical statements by entering the letters A through F on the appropriate boxes:
s′′<0.
s′ is constant
s′<0
s′′′<0
s′′>0
s′=ks
Answer:
Answers given below.
Step-by-step explanation:
F) acceleration is the second derivative of distance with respect to time.
Thus; s'' < 0
D) Car travels the same distance in the same time interval. This means the speed is constant. Speed is the first derivative of distance with time. Thus;
s' is constant
E) Driving backwards means that speed is; s' < 0
C) Car is slowing down means negative acceleration. Thus; s'' < 0
B) Car is speeding up means acceleration is greater than 0. Thus: s'' > 0
A) Car speed being proportional to the distance it has covered means that; s' ∝ s. Thus;
s' = ks
Answer this volume based Question. I will provide 50 points + make you brainliest

Answers
Volume formulas:
Cube V = s³, (s - side),Cone V = πr²h/3, (r- radius, h- height),Sphere V = 4πr³/3, (r - radius)======================
Volume of metal, is same as the volume of the cone with radius a and height 2a:
V = πr²h/3 V = π(a²)(2a)/3 = 2πa³/3(i) The volume of the metal plank is half the volume of the metal:
V = (1/2)(2πa³/3) = πa³/3(ii) The volume of the two spheres is same as the volume of the plank, so the volume of each sphere is:
V = (1/2)πa³/3 = πa³/6The volume of sphere with radius r is 3πr³/4, compare the two and solve for r:
3πr³/4 = πa³/6r³ = 4a³/18r³ = 2a³/9r = a∛(2/9)(iii) Using the volume of the plank (cube), find the side length:
V = s³ (s- side of cube)V = πa³/3s³ = πa³/3s = a∛(π/3)(iv)
Use the formula from the previous part and substitute values of a and π to get:
a∛(π/3) = 12.5∛(3.14/3) = 12.5*1.01 = 12.6 (rounded)what is the answer pls Question 29 of 45
In the triangle below, what is the length of MN?
OA. 50
OB. 100
OC. 20
OD. 40
50
20
M
50

Answers
The calculated length of the segment MN in the triangle is 20
How to find the length of the segment MN in the triangleFrom the question, we have the following parameters that can be used in our computation:
The triangle
The third angle in the triangle is calculated as
Third angle = 180 - 50 - 50
Evaluate
Third angle = 80
The length of the segment MN is then calculated as
MN/sin(50) = 20/sin(50)
This gives
MN = sin(50) * 20/sin(50)
Evaluate
MN = 20
Hence, the length of the segment MN in the triangle is 20
Read more about law of sines at
https://brainly.com/question/30974883
#SPJ1
Lauren's science class is taking a field trip to the nearest natural history museum. The
museum is 62.5 miles from Lauren's school. The class plans to stop after 30 minutes, or 0.5
hours, to visit a local wildlife refuge. The bus driver plans to drive at an average speed of 50
miles per hour. How many hours will the second part of the trip take?
Answers
Answer:0.75
Step-by-step explanation:
i just did it
Complete the coordinate proof of the theorem.


Answers
The coordinate of C( a+c , b) , AC are ((a+c)/2 , b/2) , BD are ((a+c)/2 , b/2)
What are Coordinates ?Coordinates is the value assigned to a point in a x-y graph to determine its location.
The coordinates of parallelogram is
A ( 0,0) B (a,0) , C ( __ , ___) , D ( c , b)
The y coordinate is same as D as b
and the x coordinate will be a+c
C( a+c , b)
The coordinate of the mid point of AC are ((a+c)/2 , b/2)
The coordinate of the mid point of BD are ((a+c)/2 , b/2)
To know more about Coordinates
https://brainly.com/question/15300200
#SPJ1
A piece of wood is in the shape of a rectangular prism with a length of 10 inches, a width of 4 inches, and a height of 5 inches. You cut the wood in half to form two pieces of wood, each with a length of 5 inches. What is the percent increase in the total surface area? Round your answer to the nearest hundredth, if necessary. %
Answers
Answer: 18.18%
Step-by-step explanation:
First, let's calculate the surface area of the original piece of wood. The surface area (SA) of a rectangular prism is given by the formula:
\($$SA = 2lw + 2lh + 2wh$$\)
where \(\(l\)\) is the length, \(\(l\)\) is the width, and \(\(h\)\) is the height. For the original piece of wood, \(\(l = 10\) inches\), \(\(w = 4\) inches\), and \(\(h = 5\) inches\).
After the piece of wood is cut in half, the length becomes 5 inches, but the width and height remain the same. So, for each of the two new pieces of wood, \(\(l = 5\) inches\), \(\(w = 4\) inches\), and \(\(h = 5\) inches\). The total surface area of the two new pieces of wood is twice the surface area of one of the new pieces.
The percent increase in the total surface area is given by the formula:
\($$\text{Percent Increase} = \frac{\text{New Total SA} - \text{Original SA}}{\text{Original SA}} \times 100\%$$\)
Let's calculate these values.
The percent increase in the total surface area when the piece of wood is cut in half is approximately 18.18%.
Write the equation of the line that has a slope of -3/4 and contains the point (8,-3)
Answers
Answer:
y = -3/4x + 3
Step-by-step explanation:
lmk if you want an explanation
What is the x intercept of y=4x-8
Answers
Answer:
(2,0) is the x-intercept
Step-by-step explanation:
It's easiest if you just type this equation into a graphing caculator
The x intercept of y = 4x -8 is at x = 2 or at point (2 , 0) .
Given,
Equation of line : y=4x-8
Now,
The standard equation of line is y = mx + c
To find the x intercept put y = 0 .
x intercept is the point on x axis thus we put y coordinate as 0 at y axis .
Now substitute y = 0 in the equation of line,
y=4x-8
0 = 4x - 8
8 = 4x
x = 2
Thus the x intercept is at x = 2 or the point is (2 , 0) .
Know more about lines,
https://brainly.com/question/2696693
#SPJ2
fill in the mission numbers to make the fractions equivalent. 1/2 and /8= 4/12 and /60= 2/3 and /12= 4/4 and /8=
Answers
To make the fractions equivalent, we need to find the missing numerators that would make them equal. Let's fill in the missing numerators:
1/2 and __/8
To make the fractions equivalent, we can multiply both the numerator and denominator of the first fraction by 4:
1/2 and 4/8
Now, the fractions are equivalent.
---
4/12 and __/60
To make the fractions equivalent, we can multiply both the numerator and denominator of the first fraction by 5:
4/12 and 20/60
Now, the fractions are equivalent.
---
2/3 and __/12
To make the fractions equivalent, we can multiply both the numerator and denominator of the first fraction by 4:
2/3 and 8/12
Now, the fractions are equivalent.
---
4/4 and __/8
To make the fractions equivalent, we can multiply both the numerator and denominator of the first fraction by 2:
4/4 and 8/8
Now, the fractions are equivalent.
Find the value of x, 12=x-[-15]
Answers
Answer:
x= - 3
Step-by-step explanation:
Use Newton's Method to approximate the zero(s) of the function. Continue the iterations until two successive approximations differ by less than 0.001. Then find the zero(s) to three decimal places using a graphing utility and compare the results. f(x) = x^3 - 4.9x^2 + 6.79x - 2.871
Answers
The zero(s) of the function is 6 if the function is f(x)=x³ - 4.9x² +6.79x-2.871.
The Newton's method is use to estimate the zeros is valuable, in spite of the way that it probably won't work. The central issue here is find digression lines, and applying that equation over and over till it draws nearer to the roots.
It fits for any polynomial condition despite the fact that it is significantly more utilized, to more serious level polynomial.
*For the function given, f(x)=x³ - 4.9x² +6.79x-2.871, starting from the root is a whole number, 6, in couple of preliminaries we'll find the root, every one of them greater than 0.001 so how about we supplant the
1) Really look at chart beneath.
2) Investigating, f(x)=x³ - 4.9x² +6.79x-2.871. we can see that the root is somewhere in the range of x=5 and x=7, we definitely know is - 6.
So,we check for x=7
Plugging in the formula,we get
=>\(X_n_+_1\) = \(x_n\) - f(x)/ f'(x)
=> x₂ =7- (x³ - 4.9x² +6.79x-2.871) / (3x² -9.8x +6.79)
=>x₂=7- (-7+6) / -1
=>x₂ = 7-1
=>x₂=6
Similarly, if we find x₃ then its value will be also 6.
In the given function, the root is a whole number, every one of the approximations were number numbers and bigger than 0.001.Then again, in the event that the function had nonsensical roots, we could undoubtedly show results lesser than 0.001.
Hence,zero(s) of the given function is 6.
To know more about functions, visit here:
https://brainly.com/question/29633660
#SPJ4
inver laplace
\( {l}^{ - 1} ( \frac{s}{( {s}^{2} + 16)^{2} } ) \)
![inver laplace [tex] {l}^{ - 1} ( \frac{s}{( {s}^{2} + 16)^{2} } ) [/tex]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/tRHfsGvT8N6QSZIhrDLCyZ5m4R7EEnMV.jpeg)
Answers
Answer:
s
_______________
ls^4 + 32ls^2 + 256l
Step-by-step explanation:
I used an algebra calculator called MathPapa to solve your equation.
Also, welcome to brainly!
The length of a rectangle is eight meters more than the width. Write an Algebraic Expression to find the area.
I kinda think that this Question is incomplete but this is what my teacher gave me. Thank you for Solving.
Answers
Answer: 8xw=a
Step-by-step explanation:
w=width
a=area
y=-1/4x+3
y=-3/2x-2
Answers
Answer:
x = -4
y = 4
plz follow me
and mark me as brainlist

Toby works at an amusement park. He loads 10 new passengers onto the roller coaster every
3/4
of a minute. At what rate does Toby load passengers?
Pleaseeee
Answers
Answer:
13 1/3
Step-by-step explanation:
im sure this is right btw
helppppp meeeeeeeeeeeeeeeeeeeeeee

Answers
Answer:
D 104
Step-by-step explanation:
A and b are too small to have $71 left. C is also not enough if he had $71 left.
ariana's 150g bag of trail mix is x% raisins. brandon's 250g bag of trail mix is y% raisins. they combine the two mixes together in one bowl. *write an expression that shows the concentration of raisins in the resulting mix.
Answers
Answer:
(3x+5y)/8
Step-by-step explanation:
The total amount is 150+250=400
We then do (3x+5y)/2 × 1/400
This equals (3x+5y)/800
We multiply that by 100 giving us the final answer.
Joseline has 347 marbles. Ever has 4 times as many as Joseline. Pablo has 799 fewer than Ever. How many marbles does Pablo have? Joseline tiene 347 canicas. Ever tiene 4 veces más que Joseline. Pablo tiene 799 menos que nunca. ¿Cuántas canicas tiene Pablo?
Answers
Answer:
its D
Step-by-step explanation:
Write the fraction below as a sum or difference.
11x + 5
6
Answers
The fraction in form of sum or difference will be;
⇒ 11/6x + 5/6
What is mean by Fraction?A fraction is a part of whole number, and a way to split up a number into equal parts. Or, A number which is expressed as a quotient is called fraction. It can be written as the form of p : q, which is equivalent to p / q.
Given that;
The fraction is,
⇒ (11x + 5) / 6
Now,
Since, The fraction is,
⇒ (11x + 5) / 6
It can be written as;
⇒ (11x + 5) / 6
⇒ 11x/6 + 5/6
Thus, The fraction is written as;
⇒ 11/6x + 5/6
Learn more about the fraction visit:
https://brainly.com/question/5454147
#SPJ1
Decide whether the given ordered pair is a solution to the system of equations.
x + 5y = 8
4x − 5y = 7
(3, 1)
Answers
Answer:
Yes
Step-by-step explanation:
(3) + 5(1) = 8
4(3) - 5(1) = 12 - 5 = 7
To determine if the ordered pair (3, 1) is a solution to the system of equations:
x + 5y = 8
4x - 5y = 7
We substitute x = 3 and y = 1 into both equations and check if the equations hold true.
x + 5y = 8
3 + 5(1) = 8
3 + 5 = 8
8 = 8
This equation is true when x = 3 and y = 1.
4x - 5y = 7
4(3) - 5(1) = 7
12 - 5 = 7
7 = 7
This equation is also true when x = 3 and y = 1.
Since both equations hold true for the values x = 3 and y = 1, we can conclude that the ordered pair (3, 1) is a solution to the system of equations.
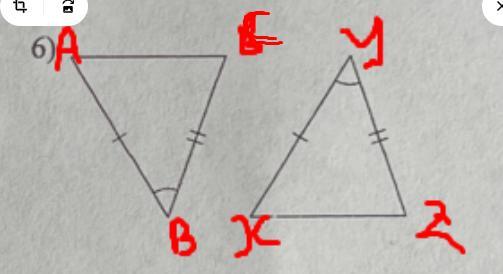
I need help on trying to find out how triangles are congruent an similar
Answers
Answer
\(\text{The two triangles are congruent by side angle side}\)\(\triangle\text{ABC}\cong\triangle\text{XYZ}\)\(\begin{gathered} \angle\text{ABC=}\angle XYZ \\ AB=XY \\ CB=YZ \end{gathered}\)\(\text{The two triangles are congruent by side angle side i.e SAS}\)