two people start walking in different directions from the same point. one walks south at 4 mph and the other walks west at 3 mph. at what rate is the distance between the walkers increasing two hours later?
Answers
The distance between the walkers will increase at the rate of 5mph.
According to the question,
Two people start walking in different direction from same point.
Speed on the person walking west = 3mph
Speed of the person walking south = 4mph
The angle formed by the point connecting two persons will be = 90 degree
Applying Pythagoreans theorem,
\(p^{2} + b^{2} = h^{2}\)
\(4^{2} + 3^{2} = h^{2}\)
\(16 + 9 = h^{2}\)
\(h^{2} = 25\)
\(h = \sqrt{25}\)
h = 5mph.
Thus after two hours, the distance between same two persons will be 10m.
Learn more about time and distance at
https://brainly.com/question/11411949
Related Questions
Find the probability of rolling a sum of 10 or a sum that is an odd number when two number cubes are rolled.
Answers
Answer:
7/12 chance
Step-by-step explanation:
(1 2 3 4 5 6)
(1 2 3 4 5 6)
All the possibilities:
(1, 1) (2, 1) (3, 1) (4, 1) (5, 1) (6, 1)
(1, 2) (2, 2) (3, 2) (4, 2) (5, 2) (6, 2)
(1, 3) (2, 3) (3, 3) (4, 3) (5, 3) (6, 3)
(1, 4) (2, 4) (3, 4) (4, 4) (5, 4) (6, 4)
(1, 5) (2, 5) (3, 5) (4, 5) (5, 5) (6, 5)
(1, 6) (2, 6) (3, 6) (4, 6) (5, 6) (6, 6)
There are 18 odd sums.
(1, 1) (2, 1) (3, 1) (4, 1) (5, 1) (6, 1)
(1, 2) (2, 2) (3, 2) (4, 2) (5, 2) (6, 2)
(1, 3) (2, 3) (3, 3) (4, 3) (5, 3) (6, 3)
(1, 4) (2, 4) (3, 4) (4, 4) (5, 4) (6, 4)
(1, 5) (2, 5) (3, 5) (4, 5) (5, 5) (6, 5)
(1, 6) (2, 6) (3, 6) (4, 6) (5, 6) (6, 6)
There are 3 possibilities whose sums add up to 10.
Since there are 36 total possibilities and 21 numbers that fit the rule of having an odd sum or a sum of 10. There is a 21/36 chance or simplified, 7/12 chance.
the major benefit of enterprise application integration is that it
Answers
The major benefit of enterprise application integration (EAI) is that it allows different applications and systems within an organization to seamlessly communicate and share data.
This integration eliminates data silos and enables real-time data exchange, leading to improved efficiency, productivity, and decision-making within the organization.
By implementing EAI, businesses can achieve the following benefits:
1. Enhanced Data Accuracy and Consistency: EAI ensures that data is synchronized and consistent across different systems, eliminating the need for manual data entry and reducing the risk of errors or discrepancies.
2. Increased Efficiency and Productivity: EAI automates the flow of information between applications, reducing the need for manual intervention and streamlining business processes.
This leads to improved efficiency and productivity as employees spend less time on repetitive tasks.
3. Improved Decision-Making: EAI provides a unified view of data from various systems, enabling better analysis and decision-making. Decision-makers have access to real-time and accurate information, allowing them to make informed and timely decisions.
4. Cost Savings: By integrating existing applications instead of developing new ones from scratch, EAI can help businesses save costs. It reduces the need for duplicate systems, minimizes data duplication, and optimizes IT infrastructure.
5. Scalability and Flexibility: EAI allows organizations to easily integrate new applications or systems as their needs evolve. It provides a flexible framework that can accommodate future growth and changes in business requirements.
Overall, the major benefit of enterprise application integration is the ability to achieve seamless connectivity and data exchange between systems, leading to improved efficiency, productivity, and decision-making in an organization.
To know more about integration refer here:
https://brainly.com/question/31744185#
#SPJ11
In an IQ test, 4 marks are given for every correct answer and 2 marks are deducted for every wrong answer. If Crystal answered 30 questions and scored 84 marks, how many of her answer were correct?
Answers
4x30=120
120-84=36
36/2=18
So the correct answer is 18.
HELLO HUMANS! QUICK QUESTION. WILL MARK AS BRAINLIEST!
How do you solve for the slope of a graph that isn't straight? How would I solve the slope for this?

Answers
9514 1404 393
Answer:
use the slope formula
Step-by-step explanation:
Usually, you are asked for an average slope over some interval. The slope is calculated on that interval the same as it would be if you were given two points, one at each end of the interval.
m = (y2 -y1)/(x2 -x1)
For example, if you wanted to know the slope on the interval [1, 2] hours, the points you would use would be ...
(hours, miles) = (1, 25) and (2, 75)
The corresponding slope on that interval is ...
m = (75 -25)/(2 -1) = 50 . . . . miles per hour
__
You can identify four (4) regions on this graph in which the slope is constant:
(0, 1) . . . slope is 25 mph
(1, 2) . . . slope is 50 mph, as computed above
(2, 3) . . . slope is 0 (the rider has stopped)
(3, 5) . . . slope is 25 mph
Over different intervals, you need to identify the points involved and use the formula to compute the average slope.
Find a polynomial function of lowest degree with rational coefficients that has the given numbers as some of its zeros. 1+i, 1 The polynomial function in expanded form is f(x) =
Answers
The polynomial function in expanded form is f(x) = x² - 3x² + 4x - 2.
A polynomial function with rational coefficients that has the given numbers as zeros, considering their conjugates . Since 1+i is a zero, its conjugate 1-i must also be a zero.
Using the zero-product property, that if a polynomial has a zero at a given number, then the polynomial must have a factor of (x - zero). Therefore, the polynomial function with the given zeros can be written as:
f(x) = (x - (1+i))(x - (1-i))(x - 1)
Expanding this expression,
f(x) = ((x - 1) - i)((x - 1) + i)(x - 1)
= ((x - 1)² - i²)(x - 1)
= ((x - 1)² + 1)(x - 1)
= (x² - 2x + 1 + 1)(x - 1)
= (x² - 2x + 2)(x - 1)
= x² - 2x² + 2x - x² + 2x - 2
= x² - 3x²+ 4x - 2
.
To know more about polynomial here
https://brainly.com/question/30464983
#SPJ4
minimum possible integral value of k such that the equation 2^2x - 2(k-1)2x+k=0 has one root less than 1 and other root greater than 1
Answers
Finding the smallest possible integer value of k requires analyzing the given equation and determining the conditions under which one root is less than 1 and the other is greater than 1.
The equation is:
2^(2x) - 2(k-1)^(2x) + k = 0
Let's break down the conditions step by step.
1. Square root less than 1:
To make the square root less than 1, we need to substitute x = 1 into the equation and get a positive value. So if x = 1, then
2^(2*1) - 2(k-1)^(2*1) + k > 0
4 - 2(k-1)^2 + k > 0
Extensions and simplifications:
4 - 2(k^2 - 2k + 1) + k > 0
4 - 2k^2 + 4k - 2 + k > 0
-2k^2 + 5k + 2 > 0
2k^2 - 5k - 2 < 0 xss=removed xss=removed xss=removed xss=removed > 0.
Now we can combine both conditions to find the smallest integer value of k.
2k^2 - 5k - 2 < 0 > 0 (Condition 2)
By solving these conditions simultaneously, we can find the range of values of k that satisfy both conditions and determine the smallest integer value of k. However, this process requires calculations and algebraic manipulations beyond the scope of simple text-based answers.
It is recommended to use an algebraic calculator or software to solve the equation and find the smallest integer value of k that satisfies the given conditions.
IMPORTANT:Kindly Heart and 5 Star this answer, thanks!Can we draw a triangle with sides 3cm 3.5 cm and 6.5 cm?
Answers
No, we cannot draw a triangle with sides 3 cm, 3.5 cm, and 6.5 cm.
Let's understand the concept behind this:
Apply the triangle's length-of-sides property, which stipulates that the total of any two sides should be more than the value of the third side. Such a triangle cannot exist if there is any pair of sides whose sum is equal to or less than the third side.
We must determine whether the supplied side lengths constitute a triangle. We now understand that the triangle's third side should be greater than the sum of any two of its sides. Such a triangle cannot exist if there is any pair of sides whose sum is equal to or less than the third side. So, we'll try every combination and see if it meets the criteria.
Let’s assume AB = 3 cm, BC = 3.5 cm and AC = 6.5 cm.
AB + AC = 3 + 6.5 cm = 9.5 cm > 3.5 cm = BC.
AC + BC = 6.5 + 3.5 = 10 cm > 3 cm = AB.
AB + BC = 3 + 3.5 cm = 6.5 cm = AC.
However, in this case, the length of the third side is equal to the total lengths of the other two sides, which renders the triangle's condition incorrect.
Therefore, there does not exist any triangle with sides of 3 cm, 3.5 cm, and 6.5 cm.
To learn more about Triangle properties, visit: https://brainly.com/question/8476788
#SPJ4
An article reports "attendance dropped 6% this year, to 252." What was the attendance before the drop?
Answers
Answer:
so Divide or subtract 252 - 6%= 236.
Step-by-step explanation:
236.
Ashanti bought seven boxes to pack all the junkie stuff in her room. A week later half of all her boxes were destroyed in a fire. There are now only 22 boxes left. How many boxes did she start with?
SHOW YOUR WORK.
Answers
Answer:
the aswer is 154
Step-by-step explanation:
multiple
Answer:
3 and half
Step-by-step explanation:
half of seven is 3.5
Step-by-step to reduce the radical of the square root Of 160
Answers
Answer:
\(4\sqrt{10}\)
Step-by-step explanation:
\(\sqrt{160}\)
\(\sqrt{16 * 10}\)
\(4\sqrt{10}\)
because 16 is a perfect square root and it splits into 4 * 4 while 10 isnt a perfect square root so it stays inside.
Answer:
4\(\sqrt{10}\\\)
Step-by-step explanation:
To reduce a radical of a square root, you want to find a perfect square that multiplies into that number. 16 is a perfect square (of 4) and can be divided into 160. so \(\sqrt{160\\}\) becomes \(\sqrt{16}\) x \(\sqrt{10}\) (because 16 x 10 = 160) then we simplify the square root of 16 to be 4. We leave the square root of 10 because it cannot be simplified.
Hope this helps!
:)
The length of a rectangle is six times its width. If the area of the rectangle is 384^2, find its perimeter.
Answers
Answer:
Perimeter, P = 112 meters
Step-by-step explanation:
Let the length of the rectangle be L.Let the width of the rectangle be W.Translating the word problem into an algebraic expression, we have;
L = 6W ...... equation 1
Given the following data;
Area of rectangle = 384 m²To find the perimeter of the rectangle;
First of all, we would determine the dimensions of the rectangle using its area.
Mathematically, the area of a rectangle is given by the formula;
Area of rectangle = LW ..... equation 2
Substituting eqn 1 into eqn 2, we have;
384 = 6W(W)
384 = 6W²
Dividing both sides by 6, we have;
W² = 384/6
W² = 64
Taking the square root of both sides, we have;
W = √64
Width, W = 8 meters
Next, we would find the length;
L = 6W
L = 6 * 8
Length, L = 48 meters
Lastly, we would determine the perimeter of the rectangle using the above dimensions;
Mathematically, the perimeter of a rectangle is given by the formula;
Perimeter = 2(L + W)
Substituting the values into the formula, we have;
Perimeter, P = 2(48 + 8)
Perimeter, P = 2(56)
Perimeter, P = 112 meters
a newsletter publisher believes that 50p% of their readers own a laptop. a testing firm believes this is inaccurate and performs a test to dispute the publisher's claim. after performing a test at the 0.050.05 level of significance, the testing firm decides to reject the null hypothesis. what is the conclusion regarding the publisher's claim?
Answers
The conclusion regarding the publisher's claim is that it is not valid. When the testing firm rejected the null hypothesis after performing a test at the 0.05 level of significance.
Therefore, the claim that 50% of their readers own a laptop by the newsletter publisher is not true. A null hypothesis is a statement that is being tested for possible rejection under the assumption that it is true. It is often symbolized as H0. A one-tailed test examines only one side of the distribution, while a two-tailed test examines both sides.
For a one-tailed test, the null hypothesis is rejected if the sample statistic is at the extremes of the distribution (either in the upper or lower tail). On the other hand, for a two-tailed test, the null hypothesis is rejected if the sample statistic is at the extremes of both tails.The level of significance, denoted as alpha (α), is the probability of committing a Type I error. A Type I error is the rejection of a null hypothesis that is true. Alpha is typically set to 0.05 or 0.01. A p-value is a probability that is calculated from the test statistics.
To know more about conclusion visit:
https://brainly.com/question/28832812
#SPJ11
Solve.
\( \frac{ \sqrt{5} + \sqrt{3} }{ \sqrt{5} - \sqrt{3} } + \frac{ \sqrt{5} - \sqrt{3} }{ \sqrt{5} + \sqrt{3} } \)
Solve.
Answers
Step-by-step explanation:
Hope it will help you a lot.
![Solve.[tex] \frac{ \sqrt{5} + \sqrt{3} }{ \sqrt{5} - \sqrt{3} } + \frac{ \sqrt{5} - \sqrt{3} }{ \sqrt{5}](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/Qyqi0ifCbL6v65JhhQlTadI8hDs8sspq.jpeg)
Use the Distributive Property to write an equivalent expression for the expression (a + b)(2 + y).
Answers
Answer:
2a+ay+2b+by
We multiple the first number by the two numbers in the next parentheses
Answer:
\(2a+2b+ay+ab\)
Step-by-step explanation:
\((a+b)(2+y)\\(2a+ay+2b+by)\\(2a + 2b+ay+ab)\)
a minus 5.36 = 1.04 solve for a what is it
Answers
Answer:
A = 6.4
Step-by-step explanation:
A - 5.36 = 1.04
+5.36 +5.36
A = 6.4
On an exam for a class with 32 students, the mean score was 67.2 points. The instructor rescored the exam by adding 8 points to the exam score for every student. What was the mean of the scores on the rescored exam?
Answers
The mean score on the rescored exam is 75.5 points.
To find the mean of the rescored exam, we need to add 8 points to each student's score and then find the new mean.
To do this, we can use the formula:
New Mean = (Sum of Rescored Scores) / Number of Students
We know that there are 32 students and the original mean score was 67.2 points.
So the sum of the original scores is:
Sum of Original Scores = Mean x Number of Students
= 67.2 x 32
= 2144.
To find the sum of the rescored scores, we need to add 8 points to each student's score:
Sum of Rescored Scores = Sum of Original Scores + (8 x Number of Students)
= 2144 + (8 x 32)
= 2416.
Now we can find the new mean:
New Mean = Sum of Rescored Scores / Number of Students
= 2416 / 32
= 75.5.
Therefore, the mean score on the rescored exam is 75.5 points.
To learn more about mean score here:
https://brainly.com/question/15931564#
#SPJ11
\( 2 x=3 y+4,5 x-6 y=-1 \); solve for \( x \) (put the first equation in the form \( a x+b y=c \) ).
Answers
To solve for \(\(x\) and \(y\)\), we can use the method of substitution or elimination. hus, we have successfully put the first equation in the required form. Now we need to solve this system of equations to find the value of x. Substituting the value of 2x from equation
Given equations:
Equation \((1): \(2x = 3y + 4\)\)
Let's solve it using the substitution method:
From equation (1), we can express \(x\) in terms of \(y\):
\(\(2x = 3y + 4\)\)
Dividing both sides by 2, we get:
\(\(x = \frac{3}{2}y + 2\)\)
Now, substitute this value of \(x\) into equation (2):
\(\(5x - 6y = -1\)\)
\(\(5\left(\frac{3}{2}y + 2\right) - 6y = -1\)\)
Simplifying the equation:
\(\(\frac{15}{2}y + 10 - 6y = -1\)\)
Combine like terms:
\(\(\frac{3}{2}y + 10 = -1\)\)
Subtract 10 from both sides:
\(\(\frac{3}{2}y = -11\)\)
Substitute the value of \(y\) back into equation (1):
\(\(2x = 3\left(-\frac{22}{3}\right) + 4\)\)
Therefore, the correct solution to the given system of equations is:
\(\(x = -20\) and \(y = -\frac{22}{3}\).\).
To know more about equation visit:
https://brainly.com/question/29657983
#SPJ11
please help no work needs to be shown

Answers
Answer:
I would say a 20, 30-ish degree angle, maybe 45 degrees, somewhere in that continuum
If you have to divide by a variable, be sure to explain why it is not zero or why it cannot be zero
1. Let A(x,y,z) = 12 +3+ y2 - 2y MULTIPLIERS
(a) Find the global maximum and minimum of A(3,7.2) subject to the constraint ar* + y + z = 2
(b) Find the global maximum and minimum of Als, y.) on the closed bounded dornain ** + y + x2 <16.
Answers
(a) There is no extreme value of A subject to the given constraint,
(b) For x = 0, y + z² ≤ 16.
y is between -4 and 4. In this case, f(y,z) = y² and the maximum value is 16.
For x = ±y, z = 4 - y².
y is between -2 and 2. In this case, f(y,z) = 2y² - y⁴ and the maximum value is 2.
When dividing by a variable, one should always keep in mind that the variable cannot be equal to zero. In other words, if the value of the variable is zero, the function or expression will not be defined or will give an undefined result. The reason is that division by zero is not defined in the set of real numbers.
Therefore, one should exclude the value of zero from the domain of the function or expression.
In part (a) of the given question, we are asked to find the global maximum and minimum of A(x,y,z) = 12 + 3x + y² - 2y subject to the constraint x + y + z = 2.
Let's find the partial derivatives of A with respect to x, y, and z.
∂A/∂x = 3
∂A/∂y = 2y - 2 = 2(y - 1)
∂A/∂z = 0
Now, we have to solve the system of equations consisting of the partial derivatives and the constraint equation.
\(3 = \lambda_1 + \lambda_2,\\2y - 2 = \lambda_1 + \lambda_2,\\\lambda_1x + \lambda_2x = 0,\\\lambda_1y + \lambda_2y - 1 = 0,\\\lambda_1z + \lambda_2z = 1.\)
Substituting the values of the partial derivatives, we get:
\(\lambda_1 + \lambda_2 = 3,\\\lambda_1 + \lambda_2 = -2,\\\lambda_1(3) + \lambda_2(0) = 0,\\\lambda_1(y - 1) + \lambda_2(y - 1) = 0,\\\lambda_1(0) + \lambda_2(1) = 1.\)
The second and third equations are contradictory. So, under the given constraint, A has no extreme value.
In part (b), we are asked to find the global maximum and minimum of A(x,y,z) = x² + y² on the closed bounded domain x² + y + z² ≤ 16.
Let's use the method of Lagrange multipliers to solve the problem. We have to find the critical points of the function f(x,y,z) = x² + y² subject to the constraint x² + y + z² = 16.
We have to solve the system of equations consisting of the partial derivatives of f, the partial derivatives of the constraint function, and the equation of the constraint function.
2x = λ(2x),
2y = λ(1),
2z = λ(2z).
Substituting the value of λ from the second equation into the first equation, we get: x = 0 or x = ±y.
Substituting the values of x and λ from the first and second equations into the third equation, we get:
z = 4 - y² or z = 0.
Since the constraint is x² + y + z² ≤ 16, we have to consider the following cases:
Case 1: x = 0, y + z² ≤ 16.
So, y is between -4 and 4. The maximum value of f(y,z)=y² is 16 in this case.
Case 2: x = ±y, z = 4 - y².
So, y is between -2 and 2. The maximum value of f(y,z) = 2y² - y⁴ is 2 in this case.
To know more about maximum value: https://brainly.com/question/30096512
#SPJ11
Using the following image, solve for JI.
J
2x + 28
x + 22
5
H
Answers
In the given image, the length of JI is 6
Solving linear equationsFrom the question, we are to solve for JI
From the given image, we can write that
JI + IH = JH
Then,
2x + 28 + 5 = x + 22
Solving for x
2x + 28 + 5 = x + 22
First, collect like terms
2x - x = 22 - 28 - 5
Simplifying
x = -11
But,
JI = 2x + 28
∴ JI = 2(-11) + 28
JI = -22 + 28
JI = 6
Hence, the length of JI is 6
Learn more on Linear equations here: https://brainly.com/question/27979747
#SPJ1

Is the following a property that holds for all non-decreasing positive functions f and g? (True=Yes/ False=No)
If f(n) = O(n2) and g(n) = Theta(n2), then f(n) = O(g(n)).
Answers
The answer to the question is True. This can be answered by the concept of Trigonometry.
First, let's recall the definitions of the asymptotic notations used in the question
f(n) = O(n²) means that there exists a positive constant c and a positive integer N such that f(n) <= c × n² for all n >= N.
g(n) = Theta(n²) means that there exist positive constants c1, c2, and a positive integer N such that c1 × n² <= g(n) <= c2 × n² for all n >= N.
Now, since f and g are non-decreasing positive functions, we can assume without loss of generality that N > 0 and c1 > 0. Then, for all n >= N, we have:
f(n) <= c × n² (by the definition of O notation)
c1 × n² <= g(n) <= c2 × n² (by the definition of Theta notation)
Multiplying the first inequality by c1, we get:
c1 × f(n) <= c × c1 × n²
Since c1 and n^2 are positive, we can divide both sides by n² to obtain:
c1 × (f(n) / n²) <= c × c1
Now, let's define a new function h(n) = f(n) / n². Since f(n) and n² are both non-decreasing positive functions, h(n) is also non-decreasing and positive. Moreover, for all n >= N, we have:
h(n) <= (c × c1) / c1 = c
Therefore, we have shown that there exists a positive constant c and a positive integer N such that h(n) <= c for all n >= N. This means that h(n) = O(1).
Using this result, we can conclude that:
f(n) = h(n) × n² = O(1) × n² = O(n²)
Therefore, we have:
f(n) = O(n²) and g(n) = Theta(n²) => f(n) = O(g(n))
Therefore, the answer to the question is True.
To learn more about Trigonometry here:
brainly.com/question/28863906#
#SPJ11
1.1x - 2 = 9.1 what is x
Answers
1.1x + 8 = 9.1
Reorder the terms:
8 + 1.1x = 9.1
Solving
8 + 1.1x = 9.1
Solving for variable 'x'.
Move all terms containing x to the left, all other terms to the right.
Add '-8' to each side of the equation.
8 + -8 + 1.1x = 9.1 + -8
Combine like terms: 8 + -8 = 0
0 + 1.1x = 9.1 + -8
1.1x = 9.1 + -8
Combine like terms: 9.1 + -8 = 1.1
1.1x = 1.1
Divide each side by '1.1'.
x = 1
Simplifying
x = 1
Answer:
my algebra calculator says that x=10.09
the .09 has a line over it btw!

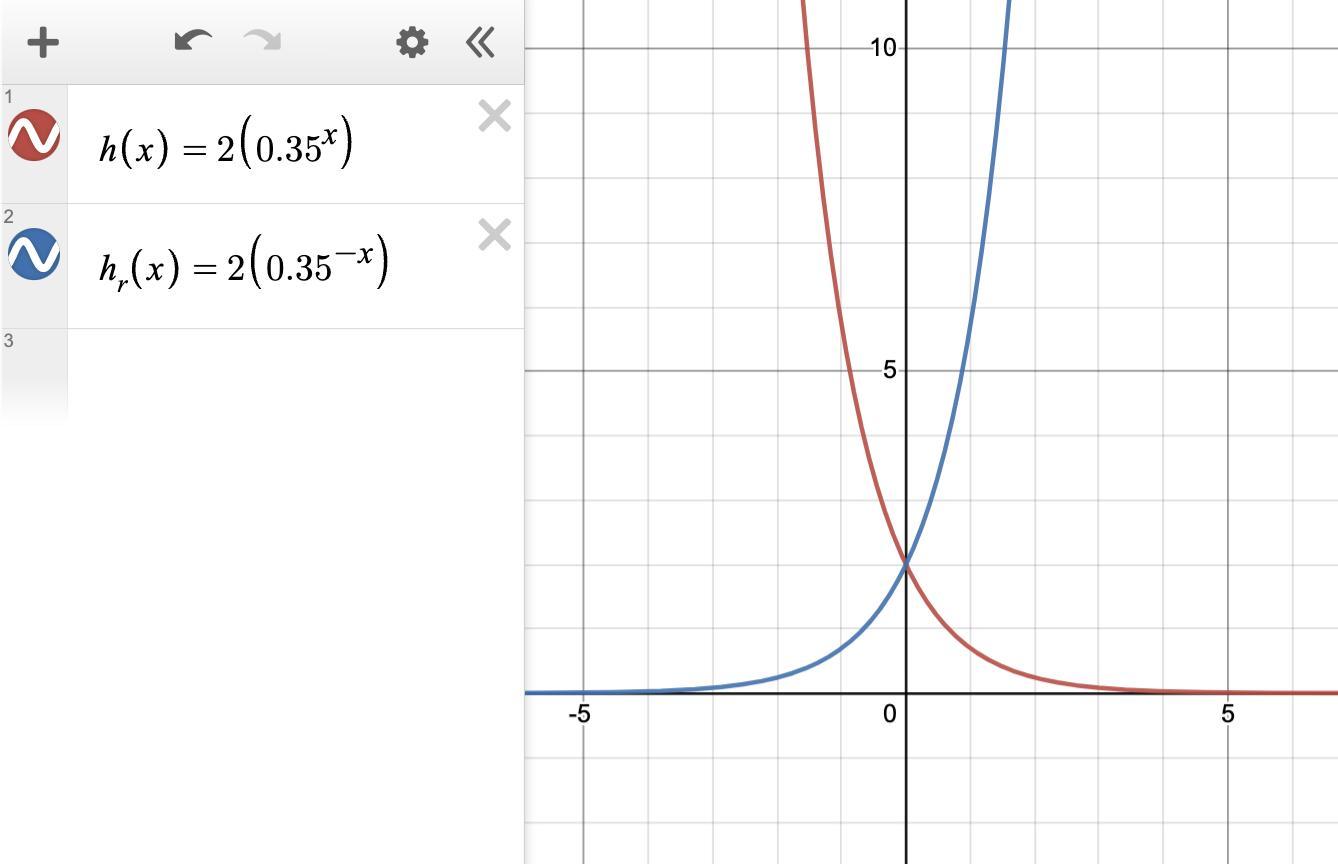
Which function represents a reflection of f(x) = 2(0. 35)x over the y-axis?
h(x) = 2(0. 35)x
h(x) = –2(0. 35)x
h(x) = 2(0. 35)–x
h(x) = 2(–0. 35)–x
Answers
Answer:
(c) h(x) = 2(0. 35)^–x
Step-by-step explanation:
You want to know the function that is a reflection of f(x) = 2(0.35^x) over the y-axis.
Reflection in y-axisWhen a point is reflected across the y-axis, the sign of its x-coordinate is changed. The y-coordinate is unchanged.
For a function y = f(x), the reflected function is y = f(-x).
For h(x) = 2(0.35^x), the reflected function is ...
h(x) = 2(0.35^-x)
<95141404393>
d) The given pie chart shows the composition of different materials in a type of cloth in percent. i) Calculate the percentage of each material found in the cloth. ii) Calculate the weight of each material contained by a bundle of 50 kg of cloth. Cotton 90° Nylon 54° Polyester 144° Others 72°
Answers
In a bundle of 50 kg of cloth, the weight of each material is:
Cotton: 12.5 kg
Nylon: 7.5 kg
Polyester: 20 kg
Others: 10 kg
To calculate the percentage of each material found in the cloth, we need to convert the given angles in the pie chart into percentages.
i) Calculating the percentage of each material:
Cotton: 90° / 360° * 100% = 25%
Nylon: 54° / 360° * 100% = 15%
Polyester: 144° / 360° * 100% = 40%
Others: 72° / 360° * 100% = 20%
Therefore, the percentage of each material found in the cloth is:
Cotton: 25%
Nylon: 15%
Polyester: 40%
Others: 20%
ii) To calculate the weight of each material contained in a bundle of 50 kg of cloth, we need to multiply the percentage of each material by the total weight.
Weight of Cotton = 25% * 50 kg = 0.25 * 50 kg = 12.5 kg
Weight of Nylon = 15% * 50 kg = 0.15 * 50 kg = 7.5 kg
Weight of Polyester = 40% * 50 kg = 0.40 * 50 kg = 20 kg
Weight of Others = 20% * 50 kg = 0.20 * 50 kg = 10 kg
for such more question on percentage
https://brainly.com/question/24877689
#SPJ8
21. If x: y = 3: 4, find (3x + 4y): (5x + 6y).
please fast answer I will mark you brain list answer
Answers
Answer: Correct option is B)
Put x=3y=4
(3x+4y):(5x+6y)=(3×3+4×4):(5×3+6×4)
=(9+16):(15+24)
=25:39
Step-by-step explanation:
The table shows values for a quadratic function.
x,y
0,0
1,2
2,8
3,18
4,32
5,50
6,72
What is the average rate of change for this function for
the interval from x= 1 to x= 3?
A. 6
B. 4
C. 8
D. 9
Answers
The a = 0.Substituting the values of a, b, and c in the general equation, we get:y = 0x² + 2x + 3The quadratic function is:y = 2x + 3Answer: The quadratic function is y = 2x + 3.
The given table illustrates the values of a quadratic function. Here is how you can find the quadratic function:Step 1: Write the general form of a quadratic function y = ax² + bx + c, where y is the dependent variable and x is the independent variable. a, b, and c are constants that affect the shape and position of the parabola.Step 2: Substitute the values from the table for x and y to form a system of equations.Step 3: Solve the system of equations to find the values of a, b, and c. Once you have found these values, substitute them into the quadratic equation to get the quadratic function.
The given table is as follows:x | 0 | 2 | 4 | 6y | 3 | 1 | -1 | -3Step 2:Form a system of equations using the values in the table. Here are the equations:y = a(0)² + b(0) + cy = a(2)² + b(2) + cy = a(4)² + b(4) + cy = a(6)² + b(6) + cStep 3:Solve the system of equations.Using the first equation, y = c. Hence, we have:y = 0²a + 0b + c3 = cThe value of c is 3.Using the second equation, we have:y = 2²a + 2b + 3y = 4a + 2b + 3Subtracting the two equations, we get:- 2a - b = - 2a + b = 2b = 4Therefore, b = 2.Substituting the values of b and c into the first equation, we get:3 = a(0)² + 2(0) + 3
for more search question equation
https://brainly.com/question/29174899
#SPJ8
Calculate the constant of variation if y varies directly as x.
y = -3
x = 2
-\(\frac{3}{2}\)
-\(\frac{2}{3}\)
-1
-6
Plsss help thankss
Answers
Answer:
-³/₂Step-by-step explanation:
y = ax
-3 = a×2 {divide both sides by 2}
a = -³/₂
let f(x) = x3 2x2 7x − 11 and g(x) = 3f(x). which of the following describes g as a function of f and gives the correct rule?
Answers
The correct rule to describe the function g as a function of f and gives the correct rule is that g(x) = 3x³-6x²+21x-33.
This function is obtained by multiplying the function f(x) by a constant, which in this case is 3.
The correct rule to describe the function
g(x) = 3f(x)
in terms of the function f(x) = x³-2x²+7x-11 is that
g(x) = 3(x³-2x²+7x-11) and thus
g(x) = 3x³-6x²+21x-33.
In order to obtain the function g(x) from the given function f(x), it is necessary to multiply it by a constant, in this case 3.
Therefore, g(x) = 3f(x) means that g(x) is three times f(x).
Thus, we can obtain g(x) as follows:
g(x) = 3f(x) = 3(x³-2x²+7x-11) = 3x³-6x²+21x-33
Therefore, the correct rule to describe the function g as a function of f and gives the correct rule is that
g(x) = 3x³-6x²+21x-33.
This function is obtained by multiplying the function f(x) by a constant, which in this case is 3.
To know more about function visit:
https://brainly.com/question/30721594
#SPJ11
Solve: -5-(-8)
ILL GIVE YOU 15 POINTS IF YOU HELP, ill mark you brainiest to
Answers
Answer:
3
Step-by-step explanation:
-5 + 8 = 3
keep inverse opposite:
-5 => -5
- => +
-8 => 8
what is the sum of 3/ X + 4/ X squared
Answers
Answer:
Step-by-step explanation:
2