two trains leave towns 831 kilometers apart at the same time and travel toward each other. one train travels 15 km/h faster than the other. if they meet in 3 hours what is the rate of each train?
Answers
Two trains leave towns 831 kilometers apart at the same time and travel toward each other.
Distance = d = 831 km
One train travels 15 km/h faster than the other.
Let the speed of the slower train is x km/h
Then the speed of the faster train is (x + 15) km/h
If they meet in 3 hours what is the rate of each train?
Time = t = 3 hours
Recall that the relationship between speed, distance, and time is given by
\(d=s\cdot t\)So we can write
\(831=(x+x+15)\cdot3_{}\)Where x is the speed of the slower train and x+15 is the speed of the faster train.
Let us solve the above equation
\(undefined\)Related Questions
What is 3 3/4 ft to yards as a mixed number?
Answers
The value of 3¾ft in yards would be = 1 6/25 yard
What is a mixed number?A mixed number is the type of number that is made up of three parts such as the whole number, a numerator and a denominator.
To convert to yards;
1 ft = 0.33 yard
3¾ = X yards
make x yards the subject of formula;
X yards = 3¾ × 0.33
X yards = 3.75×0.33
X yards = 1.24 yards
X yards in mixed number= 124/100 = 31/25 = 1 6/25 yard.
Note that the final value which is 124/100 is reduce to the lower figure by dividing through with 4 to arrive at the mixed number 1⁶/25
Learn more about mixed numbers here:
https://brainly.com/question/21610929
#SPJ1
There are six pizzas there are 36 players on the team. If each member has one slice and each pizza has eight slices how much pizza in fraction form will be left over.
Answers
There will be 12 slices of pizza left over, which can be expressed as 3/2 or 1 1/2 slices in fraction form.
To find out how much pizza will be left over, we need to calculate the total number of slices available and subtract the number of slices consumed by the players.
Given that there are six pizzas and each pizza has eight slices, the total number of slices available is 6 pizzas * 8 slices/pizza = 48 slices.
Since there are 36 players on the team, and each player has one slice, the total number of slices consumed is 36 slices.
To determine the remaining slices, we subtract the consumed slices from the total available slices: 48 slices - 36 slices = 12 slices.
Therefore, there will be 12 slices of pizza left over.
To express this as a fraction, we can write it as 12/1, which simplifies to 12. This means there will be 12 whole slices of pizza left over.
If you would like to express it as a fraction in its simplest form, you can write it as 12/8. By dividing both the numerator and denominator by their greatest common divisor, which is 4, we get 3/2. So, in fraction form, there will be 3/2 or 1 1/2 slices of pizza left over.
for more questions on fraction
https://brainly.com/question/78672
#SPJ8
Graph slope =-3 y-intercept=4
Answers
Answer:
Step-by-step explanation:
slope intercept: y = mx + b
where m is the slope and b is the y-intercept
Equation: y = -3x + 4
Since y-intercept is given, then we have the first point of the line as (0,4)
Let's find the value of x when y is 0
y = -3x + 4
0 = -3x + 4
3x = 4
x = 4/3
(4/3,0) ---second point
Since there are two points/coordinates already then we can now plot/graph.

compare the following pairs of numbers. in each pair,state which is greater

Answers
a. 759
b. 8769
c. 96699
d. 36754209
The trick is looking at the first numbers for either possible answer. Pick the one that is the greatest going backward. If you're stuck with the same numbers as in d, just continue going back until you see something like the 7 being greater than the 5.
please answer this question

Answers
Given that the variables are complex numbers, the value of the complex expression \(\frac{\gamma}{\alpha} +\bar{\frac{\alpha}{\beta}}\) is -2
How to solve the complex expression?The given parameters are:
\(\alpha + \beta + \gamma = 0\)
\(\frac{1}{\alpha} + \frac{1}{\beta} + \frac{1}{\gamma} = 0\)
Rewrite the first equation as:
\(\alpha + \beta = - \gamma\)
Take LCM in the second equation
\(\frac{\alpha + \beta}{\alpha \beta} + \frac{1}{\gamma} = 0\)
So, we have:
\(\frac{ - \gamma}{\alpha \beta} + \frac{1}{\gamma} = 0\)
Rewrite as:
\(\frac{1}{\gamma} = \frac{\gamma}{\alpha \beta}\)
Multiply through by \(\alpha\)
\(\frac{\alpha}{\gamma} = \frac{\gamma}{\beta}\)
Inverse both sides
\(\frac{\gamma}{\alpha} = \frac{\beta}{\gamma}\)
Make \(\beta\) the subject in \(\alpha + \beta + \gamma = 0\)
\(\beta =-(\alpha + \gamma)\)
So, we have:
\(\frac{\gamma}{\alpha} = \frac{-(\alpha + \gamma)}{\gamma}\)
Expand
\(\frac{\gamma}{\alpha} = -\frac{\alpha}{\gamma}- 1\)
This gives
\(\frac{\gamma}{\alpha} +\frac{\alpha}{\gamma} = - 1\)
Make \(\gamma\) the subject in \(\alpha + \beta + \gamma = 0\)
\(\gamma = -(\beta + \alpha)\)
So, we have:
\(\frac{\gamma}{\alpha} +\frac{\alpha}{-(\beta + \alpha)} = - 1\)
Split
\(\frac{\gamma}{\alpha} +\bar{\frac{\alpha}{\beta}} + \frac{\alpha}{\alpha} = - 1\)
Evaluate the quotient
\(\frac{\gamma}{\alpha} +\bar{\frac{\alpha}{\beta}} + 1 = - 1\)
Subtract 1 from both sides
\(\frac{\gamma}{\alpha} +\bar{\frac{\alpha}{\beta}} = - 2\)
Hence, the value of \(\frac{\gamma}{\alpha} +\bar{\frac{\alpha}{\beta}}\) is -2
Read more about complex numbers at:
https://brainly.com/question/10662770
#SPJ1
Solve the following equation for
�
b. Be sure to take into account whether a letter is capitalized or not.

Answers
The solution for b is: b = r * (f - h²).
What is Equation?the definition of an equation is a mathematical statement that demonstrates that two mathematical expressions are equal. For instance, the equation 3x + 5 = 14 consists of the two expressions 3x + 5 and 14, which are separated by the 'equal' symbol.
According to question:To solve for b, we need to isolate the variable b on one side of the equation. We can do that by multiplying both sides of the equation by (f - h²):
\($\frac{b}{(f - h^2)} = r * (f - h^2)\)
Now, we can isolate b by multiplying both sides by (f - h^2) again:
b = r * (f - h²)
Therefore, the solution for b is: b = r * (f - h²).
To know more about Equation visit:
brainly.com/question/28243079
#SPJ1
Find parametric equations for the tangent line to the curve with the given parametric equations at the specified point. Illustrate by graphing both the curve and the tangent line on a common screen. x=t, y=e^-t, z=2t-t^2; (0, 1, 0)
Answers
Answer:
\(x = t\)
\(y = 1 - t\)
\(z = 2t\)
Step-by-step explanation:
Given
\(x=t\)
\(y=e^{-t}\)
\(z=2t-t^2\)
(0, 1, 0)
The vector equation is given as:
\(r(t) = (x,y,z)\)
Substitute values for x, y and z
\(r(t) = (t,\ e^{-t},\ 2t - t^2)\)
Differentiate:
\(r'(t) = (1,\ -e^{-t},\ 2 - 2t)\)
The parametric value that corresponds to (0, 1, 0) is:
\(t = 0\)
Substitute 0 for t in r'(t)
\(r'(t) = (1,\ -e^{-t},\ 2 - 2t)\)
\(r'(0) = (1,\ -e^{-0},\ 2 - 2*0)\)
\(r'(0) = (1,\ -1,\ 2 - 0)\)
\(r'(0) = (1,\ -1,\ 2)\)
The tangent line passes through (0, 1, 0) and the tangent line is parallel to r'(0)
It should be noted that:
The equation of a line through position vector a and parallel to vector v is given as:
\(r(t) = a + tv\)
Such that:
\(a = (0,1,0)\) and \(v = r'(0) = (1,-1,2)\)
The equation becomes:
\(r(t) = (0,1,0) + t(1,-1,2)\)
\(r(t) = (0,1,0) + (t,-t,2t)\)
\(r(t) = (0+t,1-t,0+2t)\)
\(r(t) = (t,1-t,2t)\)
By comparison:
\(r(t) = (x,y,z)\) and \(r(t) = (t,1-t,2t)\)
The parametric equations for the tangent line are:
\(x = t\)
\(y = 1 - t\)
\(z = 2t\)

A container built for transatlantic shipping is constructed in the shape of a right rectangular prism. Its dimensions are 2 ft by 2 ft by 12.5 ft. If the container is entirely full and, on average, its contents weigh 0.22 pounds per cubic foot, find the total weight of the contents. Round your answer to the nearest pound if necessary.
Answers
Answer:
38.81 pounds
Step-by-step explanation:
Considering the definition of right rectangular prism and its volume, the total weight of the contents is 38.81 pounds.
Right rectangular prism
A right rectangular prism (or cuboid) is a polyhedron whose surface is formed by two equal and parallel rectangles called bases and by four lateral faces that are also parallel rectangles and equal two to two.
Volume of right rectangular prism
To calculate the volume of the rectangular prism, it is necessary to find the product of its dimensions, or of the three edges that converge at a certain vertex.
That is, to calculate the volume of a rectangular prism, multiply its 3 dimensions: length×width×height.
Volume of the container
In this case, you know that:
the dimensions of the container built are 7.5 ft by 11.5 ft by 3 ft.
the container is entirely full and, on average, its contents weigh 0.15 pounds per cubic foot.
So, the volume of the container is calculated as:
7.5 ft× 11.5 ft× 3 ft= 258.75 ft³
Then, the total weight of the contents is calculated as:
258.75 ft³× 0.15 pounds per cubic foot= 38.8125 pounds≅ 38.81 pounds
Finally, the total weight of the contents is 38.81 pounds.
I need help on this! It’s due at 2:00 pm today help!!

Answers
Total questions =10
Both part correct earns 5 points
One part correct earns 2 ponts
No parts correct earns - 1 points
P I-squared
Both = 4
One = 2
None = 4
Total points = (5×4) + (2×2) + (-1×4)
= 20 + 4 - 4
= 20
Point per question = 20/10 = 2Euler circles
Both = 2
One = 6
None = 2
Total points = (5×2) + (2×6) + (-1×2)
= 10 + 12 - 2
= 20
Point per question = 20/10 = 2Both team got equal points...Hope this will help....
Ella can read 2 pages in 3
minutes. How long will it take her
to read 45 pages ?
Answers
Answer:
15 minutes
Step-by-step explanation:
2 pages = 3 minutes
45 pages = 3x minutes
45 / 3 = 15
What is the range of y= tan x?
OA. All real numbers
OB. z+TTT
c. -1≤ y ≤1
D. −1≤ x ≤ 1
Answers
Answer: The range of the tangent function is (-∞,∞). So the answer is A: All real numbers.
Step-by-step explanation:
) Emily baked a cake in 42.5 minutes. She finished making dinner 9 1/10 minutes sooner than the cake. How long did it take her to make dinner? Hint: Change the 9 1/10 to a decimal
Answers
It took Emily 33.4 minutes to make dinner.
Define a mixed number?A mixed number is a kind of fraction that also has a proper fraction and a whole number. The number of whole units is represented by the whole number, and the fraction of a unit is represented by the proper fraction.
To solve the problem, we have to convert the mixed number \(9 \frac{1}{10}\) to a decimal number:
⇒ \(9 \frac{1}{10} = 9 +\frac{1}{10} = \frac{(9*10)+1}{10}\)
⇒ \(\frac{91}{10}\) = 9.1
This means that Emily finished making dinner 9.1 minutes sooner than the cake.
To find out how long it took Emily to make dinner, we can subtract 9.1 from the cake baking time:
⇒ 42.5 - 9.1 = 33.4 minutes
Therefore, it took Emily 33.4 minutes to make dinner.
To know more about mixed number, visit:
https://brainly.com/question/414559
#SPJ1
HELPPPP ???
Select the correct statement about the system of equations.

Answers
the answer is letter d)
if u arrange it correctly it will be -x +2y=2
-½x+y=1
then multiply -½ by the first equation and multiply -1 by the second equation..
then change the signs of the second equation
then cancel x .. then y =1
then substitute y with 1
..it won't be correct
Please help it’s due today!!!!

Answers
4. RSTU is a trapezoid because the opposite sides RS and UT are parallel.
5. RSTU is not an isosceles trapezoid because the diagonals are not congruent.
How to verify that RSTU is a trapezoid?In order to verify that RSTU is a trapezoid, we would have to determine slope of the pair of opposite sides and check whether at least one pair of opposite sides are parallel;
RU ║ ST
Slope of side RU = Slope of side ST
Slope of RU = (y₂ - y₁)/(x₂ - x₁)
Slope of RU = (1 + 3)/(5 + 3)
Slope of RU = 4/8
Slope of RU = 0.5.
Slope of RS = (y₂ - y₁)/(x₂ - x₁)
Slope of RS = (-9 + 3)/(-4 + 3)
Slope of RS = -6/-1
Slope of RS = 6.
Slope of ST = (y₂ - y₁)/(x₂ - x₁)
Slope of ST = (-2 - 1)/(10 - 5)
Slope of ST = -3/5
Slope of ST = -0.6.
Slope of UT = (y₂ - y₁)/(x₂ - x₁)
Slope of UT = (-2 + 9)/(10 + 4)
Slope of UT = 7/14
Slope of UT = 0.5.
Therefore, RSTU is a trapezoid because the opposite sides RS and UT are parallel.
Question 5.
In order to determine whether RSTU is an isosceles trapezoid, we would have to determine length of the diagonals by using the distance formula and check whether they are congruent;
Distance = √[(x₂ - x₁)² + (y₂ - y₁)²]
Distance RT = √[(-2 + 3)² + (10 + 3)²]
Distance RT = √170 units.
Distance = √[(x₂ - x₁)² + (y₂ - y₁)²]
Distance US = √[(5 + 4)² + (1 + 9)²]
Distance US = √181 units.
Therefore, RSTU is not an isosceles trapezoid because the diagonals RT and US are not congruent.
Read more on isosceles triangle here: brainly.com/question/19238666
#SPJ1
Review the Monthly Principal & Interest Factor chart to answer the question:
FICO Score APR 30-Year Term 20-Year Term 15-Year Term
770–789 5.5 $5.68 $6.88 $8.17
750–769 6.0 $6.00 $7.16 $8.44
730–749 6.5 $6.32 $7.46 $8.71
710–729 7.0 $6.65 $7.75 $8.99
690–709 7.5 $6.99 $8.06 $9.27
Determine the percent decrease in total principal and interest paid between a 30-year term mortgage and a 15-year mortgage with a principal balance of $484,500.00 and a 6.5% APR. Round the final answer to the nearest tenth.
31.0%
31.1%
59.0%
68.5%
Answers
The percent decrease in total principal and interest paid between a 30-year term mortgage and a 15-year mortgage with a principal balance of $484,500.00 and a 6.5% APR is 31.0%. (Option A)
How is this so ?
To calculate the percent decrease, we can use the following formula.
Percent decrease = ( (30-year factor - 15-year factor) / 30-year factor) x 100
Substituting the values from the chart.
= (($ 6.65 - $8.71) / $6.65) x 100
= ( -$ 2.06 / $6.65) * 100
= -0.309 * 100
Percent decrease ≈ - 30.9 %
Since the question asks for the percent decrease as a positive value, we take the absolute value of the result which is
Percent decrease ≈ 31%
Learn more about percentage decrease:
https://brainly.com/question/30404835
#SPJ1
What is 3-3×6+2 please?
Answers
Answer:
-13Step-by-step explanation:
What is 3-3×6+2 please?
remember PEMDAS
3 - 3 × 6 + 2 = (solve multiplication)
3 - 18 + 2 = (solve addition)
3 - 16 = (solve subtraction)
-13 (result)
Given the polynomial 9x2y6 − 25x4y8, rewrite as a product of polynomials.
(9xy3 − 25x2y4)(xy3 + x2y4)
(9xy3 − 25x2y4)(xy3 − x2y4)
(3xy3 − 5x2y4)(3xy3 + 5x2y4)
(3xy3 − 5x2y4)(3xy3 − 5x2y4)
Answers
Answer:
Option 3
(3xy³ + 5x²y⁴) (3xy³ - 5x²y⁴)
Step-by-step explanation:
Factorize polynomials:
Use exponent law:
\(\boxed{\bf a^{m*n}=(a^m)^n} \ & \\\\\boxed{\bf a^m * b^m = (a*b)^m}\)
9x²y⁶ = 3²* x² * y³*² = 3² * x² * (y³)² = (3xy³)²
25x⁴y⁸ = 5² * x²*² * y⁴*² = 5² * (x²)² * (y⁴)² = (5x²y⁴)²
Now use the identity: a² - b² = (a +b) (a -b)
Here, a = 3xy³ & b = 5x²y⁴
9x²y⁶ - 25x⁴y⁸ = 3²x²(y³)² - 5²(x²)² (y⁴)²
= (3xy³)² - (5x²y⁴)²
= (3xy³ + 5x²y⁴) (3xy³ - 5x²y⁴)
Explain how to rewrite the function shown in order to determine the transformation of the parent function. Then, describe the transformation of the graph compared to the parent function. y = ^3√-8x_4
Answers
The parent function is y = ∛x and the sequence of transformation is
Shift the function up by 4 unitsReflect across the y-axisHorizontal stretch by 1/8How to rewrite the equation of the functionFrom the question, we have the following parameters that can be used in our computation:
y = ^3√-8x_4
Rewrite the above equation properly
So, we have the following representation
y = ∛-8x - 4
Start by shifting the function up by 4 units
So, we have the following representation
y = ∛-8x - 4 + 4
Evaluate the sum
y = ∛-8x
Reflect across the y-axis
So, we have
y = ∛8x
Horizontal stretch by 1/8
This is represented as
y = ∛1/8 * 8x
So, we have
y = ∛x
Hence, the parent function is y = ∛x
Read more about transformation at
https://brainly.com/question/27224272
#SPJ1
Answer:Rewrite the equation by factoring –8 from the radicand and taking the cube root to get –2 in front of the radical symbol.
The graph is reflected over the x-axis.
The graph is also reflected over the y-axis.
The graph is vertically stretched by a factor of 2.
The graph is translated ½ unit to the left.
Step-by-step explanation:
Please help!!
If you could explain how you solved this in detail it would be much appreciated.
When x^3+kx^2+2kx+6 is divided by (x-2), the remainder is 30. Find k.
Answers
Simplifying this equation, we get:
8 + 4k + 4k + 6 = 30
8k + 14 = 30
8k = 16
k = 2
Therefore, the value of k is 1.
What is polynomial?In mathematics, a polynomial is an expression consisting of variables (usually represented by x), coefficients, and non-negative integer exponents, which are combined using the operations of addition, subtraction, and multiplication. For example,
\(3x^2 + 2x - 1\)
is a polynomial with three terms, or a "trinomial," where the variable x is raised to the powers of 2 and 1, and the coefficients are 3, 2, and -1.
The degree of a polynomial is the highest power of the variable in the expression. For example, the polynomial above has a degree of 2, since the highest power of x is 2.
Polynomials are used in many areas of mathematics, including algebra, calculus, and geometry, and are used to model many real-world phenomena.
We can use the remainder theorem, which states that if a polynomial f(x) is divided by (x - a), then the remainder is equal to f(a). In this case, we know that when the polynomial\(l x^3 + kx^2 + 2kx\) + 6 is divided by (x - 2), the remainder is 30. So, we can set up the following equation:
\(x^3 + kx^2 + 2kx + 6 = (x - 2)q(x) + 30\)
where q(x) is the quotient when. \(x^3 + kx^2 + 2kx + 6\) is divided by (x - 2). We don't need to know what q(x) is, since we're only interested in finding k.
Now, let's substitute x = 2 into the equation above:
\(2^3 + k(2^2) + 2k(2) + 6 = (2 - 2)q(2) + 30\)
Simplifying the left-hand side, we get:
\(8 + 4k + 4k + 6 = 30\)
\(16k = 16\)
\(k = 1\)
OR
8 + 4k + 4k + 6 = 30
8k + 14 = 30
8k = 16
k = 2
To know more about equation visit:
https://brainly.com/question/10413253
#SPJ1
PLS HELP ASAP ILL GIVE 5 STARS

Answers
Hey there!
(5 * 6) * 4
= 30 * 4
= 120
So you’re basically looking for something that’s equivalent to 120
CHOICE A.
5 * (5 * 6)
= 5 * 30
= 150
So, Choice A is probably NOT the answer you’re looking for!
CHOICE B.
4 * (5 * 6)
= 4 * 30
= 120
Choice B. is probably the answer you’re probably looking for.
So, I recommend you to color it apricot. :)
Good luck on your assignment and enjoy your day!
~Amphitrite1040:)
1. Which equation represents the relationship shown in the table below? (1 point)
y = -x - 3
y=x-3
y = 2x - 3
y=-2x + 3

Answers
The equation representing the relationship in the table is y = 2x - 3. The correct option is C.
What is an equation?The equation in mathematics is the relationship between the variables and the number and establishes the relationship between two or more variables.
Given data in the table:-
x y
0 -3
1 -1
2 1
3 3
The equation satisfying the values of the table will be:-
y = 2x - 3
-3 = 2 x 0 - 3=-3
-1 = 2 x 1 - 3 =-1
1 = 2 x 2 - 3 = 1
3 = 2 x 3 - 3 = 3
Therefore, the equation representing the relationship in the table is y = 2x - 3. The correct option is C.
To know more about an equation follow
https://brainly.com/question/18831322
#SPJ5
The length of a rectangle is 8 inches longer than 3 times its width. The area of the rectangle is 156 square inches.
What is the width of the rectangle?
Answers
The Answer:
Width = 6
Step-by-step explanation:
Let width be w
(3w + 8) x w = 156
3 \(w^{2}\) x 8n - 156 = 0
(w + 8 x 6) (w-6) = 0
w = 6
can i please have the answer
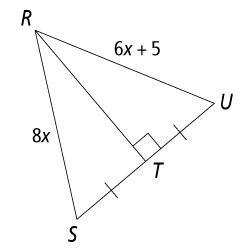
Answers
Because the triangles are congruent, we will see that x = 2.5
How to find the value of x?
Here we can see that we have two congruent triangles, RST and RTU. Because the triangles are congruent, all the correspondent sides must have equal measures.
This implies that:
RS = RU
Then, replacing the measures, we get:
8x = 6x + 5
Solving this for x we get:
8x - 6x = 5
2x = 5
x = 5/2 = 2.5
So we can conclude that x = 2.5
If you want to learn more about congruent triangles, you can read:
https://brainly.com/question/1675117
Target buys pants for $6.42 and marks up the price for customers by 70%. How much do they sell pants for?
0.7\left(6.42\right)=\$4.490.7(6.42)=$4.49
$4.49 is not the correct answer. What is the mistake? Explain.
Answers
$6.42*.70=$4.49 this is the mark up
Now $6.42+$4.49=$10.91 for the sales price
So Target sells the plants for $10.91 to their customers.
You just forgot to add the initial price to the mark-up
Hope it helps.
2x + 2 = 5x -8 simplify
Answers
Answer, x = 1
Litter such as leaves falls to the forest floor, where the action of insects and bacteria initiates the decay process. Let A be the amount of litter present, in grams per square meter, as a function of time t in years. If the litter falls at a constant rate of L grams per square meter per year, and if it decays at a constant proportional rate of k per year, then the limiting value of A is R = L/k. For this exercise and the next, we suppose that at time t = 0, the forest floor is clear of litter.
Required:
If D is the difference between the limiting value and A, so that D = R - A, then D is an exponential function of time. Find the initial value of D in terms of R.
Answers
Answer:
D = L/k
Step-by-step explanation:
Since A represents the amount of litter present in grams per square meter as a function of time in years, the net rate of litter present is
dA/dt = in flow - out flow
Since litter falls at a constant rate of L grams per square meter per year, in flow = L
Since litter decays at a constant proportional rate of k per year, the total amount of litter decay per square meter per year is A × k = Ak = out flow
So,
dA/dt = in flow - out flow
dA/dt = L - Ak
Separating the variables, we have
dA/(L - Ak) = dt
Integrating, we have
∫-kdA/-k(L - Ak) = ∫dt
1/k∫-kdA/(L - Ak) = ∫dt
1/k㏑(L - Ak) = t + C
㏑(L - Ak) = kt + kC
㏑(L - Ak) = kt + C' (C' = kC)
taking exponents of both sides, we have
\(L - Ak = e^{kt + C'} \\L - Ak = e^{kt}e^{C'}\\L - Ak = C"e^{kt} (C" = e^{C'} )\\Ak = L - C"e^{kt}\\A = \frac{L}{k} - \frac{C"}{k} e^{kt}\)
When t = 0, A(0) = 0 (since the forest floor is initially clear)
\(A = \frac{L}{k} - \frac{C"}{k} e^{kt}\\0 = \frac{L}{k} - \frac{C"}{k} e^{k0}\\0 = \frac{L}{k} - \frac{C"}{k} e^{0}\\\frac{L}{k} = \frac{C"}{k} \\C" = L\)
\(A = \frac{L}{k} - \frac{L}{k} e^{kt}\)
So, D = R - A =
\(D = \frac{L}{k} - \frac{L}{k} - \frac{L}{k} e^{kt}\\D = \frac{L}{k} e^{kt}\)
when t = 0(at initial time), the initial value of D =
\(D = \frac{L}{k} e^{kt}\\D = \frac{L}{k} e^{k0}\\D = \frac{L}{k} e^{0}\\D = \frac{L}{k}\)
Use cylindrical shells to find the volume of the solid generated when the region enclosed by the curves y=x3, x=1, and y=0 is revolved about the y-axis.
Answers
To calculate the total volume of the solid we will divide it into n shell cyline thickness of \($\Delta y$.\)
The internal shell cylinder circumference C shall be\($2 \pi r_i$\)
where r is the in The shell cylinder internal area A shall be C.
where h is the height
The volume of the shell cylinder\($\Delta v$\) shall be\($A \cdot \Delta y$.\)
Then we will have:
\(\Delta v=A \cdot \Delta y=C \cdot h \cdot \Delta y=2 \pi r_i h \cdot \Delta y \Rightarrow d v=2 \pi r_i h \cdot d y$$\)
The total volume of the solid shall be the summation of all n shell cylinders
\(\int d v=\int 2 \pi r_i h d y \Rightarrow V=\int_a^b 2 \pi r_i h d y \Rightarrow V=2 \pi \int_a^b r_i h d y$$\)
\(\int d v=\int 2 \pi r_i h d y \Rightarrow V=\int_a^b 2 \pi r_i h d y \Rightarrow V=2 \pi \int_a^b r_i h d y\)
\(The value $a$ is the value of $y$ at the point where $x=0$ then:For $x=0 \Rightarrow y=0^3 \Rightarrow y=0$ then $a=0$.The value $b$ is the value of $y$ at the point where $x=1$ then:\)
\(For $x=1 \Rightarrow y=1^3 \Rightarrow y=1$ then $b=1$.Since the integration will be with variable $y$ we have to express the function $y=x^3$ in terms of $y$ :$$\)
y=x^3 \\(Rightarrow x=\sqrt[3]{y}\)
Substituting in V, we will have:
\(V= & 2 \pi \int_a^b r_i h d y=2 \pi \int_0^1(1-y)(1-\sqrt[3]{y}) d y=2 \pi\)\\(int_0^1(1-y)\left(1-y^{\frac{1}{3}}\right) d y \\\)
&\(1-y \\& \frac{1-y^{\frac{1}{3}}}{1-y} \\& \frac{-y^{\frac{1}{3}}+y^{\frac{1}{3}} \cdot y^{\frac{1}{1}}}{} \\\)
\(& 1-y-y^{\frac{1}{3}}+y^{\frac{1}{3}+\frac{1}{1}}= \\& =1-y-y^{\frac{1}{3}}+y^{\frac{1+3}{3}}= \\\)
\(& =1-y-y^{\frac{1}{3}}+y^{\frac{4}{3}}= \\& =y^{\frac{4}{3}}-y^{\frac{1}{3}}-y+1\)
Substituting in V:
\(V=2 \pi \int_0^1\left(y^{\frac{4}{3}}-y^{\frac{1}{3}}-y+1\right) d y=2\)\({1}{3}+1}}{\frac{1}{3}+1}-\frac{y^{1+1}}\){\(1+1}+y\right]_0^1=2\) \(\pi\left[\frac{y^{\frac{4+3}{3}}}{\frac{4+3}{3}}\)-\(\frac{y^{\frac{1+3}{3}}}{\frac{1+3}{3}}-\frac{y^2}{2}+y\right]_0^1$$\)
Calculating the definite integral:
By definition\(, $\int_a^b f(x) d x=\left.F(x)\right|_a ^b=F(b)-F(a)$\) then:
\(& V=\frac{\pi}{14}\left[\left(12 \cdot 1^{\frac{7}{3}}-21 \cdot 1^{\frac{4}{3}}-14\)\(\cdot 1^2+28 \cdot 1\right)-\left(12 \cdot 0^{\frac{7}{3}}-21 \cdot\) \(0^{\frac{4}{3}}-14 \cdot 0^2+28 \cdot 0\right)\right] \\\)
& V=\(\frac{\pi}{14}[(12 \cdot 1-21 \cdot 1-14 \cdot 1+28 \cdot 1)-\underbrace{(12 \cdot 0-21 \cdot 0-14 \cdot 0+28 \cdot 0)}_0]\)
\(& V=\frac{\pi}{14}(12-21-14+28)=\frac{\pi}{14}(12+28-21-14)=\frac{\pi}{14}(40-35)=\frac{5 \pi}{14} \approx \frac{5 \cdot 3,1416}{14} \approx \frac{15,708}{14} \\& V \approx 1,122\)
Answer:\($V \approx 1,122 u . v$. (units of volume)\)
To learn more about total volume visit:
https://brainly.com/question/24852961
#SPJ4
Complete the equation of the line whose slope is -2 and y-intercept is (0, -8).
Answers
Answer:
y = -2x-8
Step-by-step explanation:
The equation for a slope is y=mx+b.
m = Slope (-2 in this case)
b = y-intercept (-8 in this case)
PLS HURRY!!! HALP PLS!!! DUE IN 10 MINS!!!
Find the AREA of the IRREGULAR figures. Show your work in a very organized way, and label your answers.
11. What is the RADIUS of ONE circle? Find the AREA of the figure.
Hint: (the circles are congruent)

Answers
Answer:
258.41 m
Step-by-step explanation:
Since there are three semi-circles in the length of the rectangle, we can divide 18 by 3 to get 6 as the diameter for each circle. The area of a semi-circle is (pi*r^2)/2, we can multiply that by 3 and add it with the area of the rectangle to get the total area.
(12*18) + (3(pi*3^2))/2 =
216 + 42.4115 =
258.41 m
15)
136⁰
2
S
?
R
Find the measure of the arc or angle indicated
Answers
Answer:
224
Step-by-step explanation:
360.-136.