Unknown Numbers
Consider the following problem.
One number is 3 less than 6 times a second number.
Their sum is 46. Find the numbers
If × represents the second number, which equation is
correct for solving this problem?
Answers
Step-by-step explanation:
y is the second number. This means we can define it as the following equations where x is the second number:
y=6x-3
y+x=46
we have a system of equations, let's move all x to the right side
y=6x-3
y=46-x
this means that 6x-3=46-x
6x+x=46+3
7x=49
x=7
now that we know x we can calculate the y through one of the equations above:
y=39
Related Questions
21% of hospital patients stay for less than 1 day. If 1,134 patients in January stay less than 1 day what total of number of patients did the hospital treat in January?
Answers
Please help I just need number 8

Answers
Answer:
Step-by-step explanation:
P=10.1
A=3.08
P=4.7+3.2+2.2 =10.1
A=1/2 b h = 1/2 (2.2)(2.8)
Find the volume of the following cone.
Round your answer to one decimal place.

Answers
Answer:
429.4 cubic units
Step-by-step explanation:
Volume of a cone = pi*r^2*(h/3)
height = 9
radius = 6.75
pi*6.75^2*(9/3) = pi*45.5625*3 = 136.6875pi
136.6875*pi is around 429.416 -> rounded = 429.4
Answer:
See answer below.
Step-by-step explanation:
\(V = \frac{1}{3} \pi r^2h\)
\(V = \frac{1}{3}\pi (6.75)^2(9)\)
\(V = 3\pi (6.75)^2\)
\(V = 136.6875\pi\)
V = 136.68.76(3.14) or use solve with calculator π
\(V = 429.19876 \\V = 429.414458\)
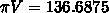
Desmond ordered his favourite pizza with 12 slices. Sadly, he could finish only %75 percent of the whole pizza.
How many pizza slices were left?
Answers
Answer:
3
Step-by-step explanation:
Left = 100% - 75% = 25%
No. of pizza slices left = 12 × 25%
= 12 × \(\frac{25}{100}\)
= 3
A bottle of water has a diameter of 3 inches and a height of 8 inches, and a mass of 1250 g. What is the volume and density?
Answers
The volume of the bottle is 56.52 cubic inches, and the density is 22.12 g/in³.
What is the volume and density of the bootle water?The volume of a cylinder is expressed as;
V = π × r² × h
Where r is radius of the circular base, h is height and π is constant pi ( π = 3.14 ).
Density is expressed mathematically as;
p = m / v
Where m is mass and v is volume.
Given that:
Diameter = 3 in
Radius r = diameter/2 = 3/2 = 1.5 in
Height h = 8 in
Mass m = 1250 g
Find the volume:
V = π × r² × h
V = 3.14 × (1.5 in )² × 8in
V = 56.52 in³
Find the density:
p = m / v
p = 1250g / 56.52 in³
p = 22.12 g/in³
Therefore, the density is 22.12 g/in³.
Learn more about density here: brainly.com/question/952755
#SPJ1
Salim had a flock of 300 chickens 15% of which are infected with a virus he plans on taking a SRS of 7 chickens to test for the virus.
Answers
Answer:0.011
Step-by-step explanation:
The probability for exact 4 chickens being infected out of the 7 is ⁷C₄(0.15)⁴(0.85)³. The correct option is (A).
How to find probability using binomial distribution?The binomial distribution is based on the binomial theorem which can be written as (a + b)ⁿ = ⁿC₀aⁿb⁰ + ⁿC₁aⁿ⁻¹b¹ + ⁿC₂aⁿ⁻²b²+ ....+ ⁿCₙa₀bⁿ.
In order to use in the probability, there should be events independent of each other and the sum of there probabilities is 1.
Given that,
The probability of the infected chicken is 15%.
Which can be written as,
P(infected) = 15%
= 15/100
= 0.15
Then, the probability of not getting infected chicken is,
P(not infected) = 1 - 0.15
= 0.85
The total number of chicken for test = 7.
Now, in order to find the probability of the exact 4 infected chickens, binomial distribution can be used as.
The general expression for binomial distribution is ⁿCₓpˣqⁿ⁻ˣ.
For the given case p = P(infected) and q = P(not infected), n = 7 and x = 4.
Thus, the probability is given as,
P(Exact 4 are infected) = ⁷C₄(0.15)⁴(0.85)³
Hence, the probability that exactly 4 of the 7 chickens sampled have the virus is ⁷C₄(0.15)⁴(0.85)³.
To know more about binomial distribution click on,
https://brainly.com/question/14565246
#SPJ2
The complete question is given as, "Salim has flock of 300 chickens, 15% of which are infected with virus: He plans on taking an SRS of 7 chickens to test for the virus_ Which of the following would find the probability that exactly 4 of the 7 chickens sampled have the virus? Choose answer: 1(0.15) '(0.85)? (0.15)*(0.85)4 300 ` (0.15)'(0.85)3 (0.15)3(0.85)4 (0.15)4(0.85)".
Absolute vale of x+2 if x is less than 2
Answers
Answer: The expression for the absolute value of x+2 when x is less than 2 is -(x+2).
Step-by-step explanation: When x is less than 2, x+2 is a negative number. The absolute value of a negative number is its opposite with the negative sign, so the absolute value of x+2 is -(x+2). Therefore, when x is less than 2, the expression for the absolute value of x+2 is -(x+2).
In 2002 the population of schoolchildren in a city was 90,000. The population decreases at a rate of 5% per year. What will be the population of school children in 2010?
Answers
Answer:
40,000 Not sure but i finish unit and got all a's and b's
Step-by-step explanation:
Answer:
59708Step-by-step explanation:
Initial population = 90000Decrease rate = 5% or 0.05 timesTime = 2010 - 2002 = 8 yearsPopulation of children in 2010:
P = 90000*(1 - 0.05)^8 = 59708 (rounded to the whole number)What the meaning of statement this?

Answers
The axiom of regularity is a set theory principle which states that every non-empty set C contains an element that is disjoint from C.
Axiom of RegularityThe set theory concept rules that for every non-empty set C there is an element x of C such that x does not intersect C. The regularity axiom aims to establish that no non-empty set will have itself as an element.
The principle which is also called the axiom of foundation is a fundamental concept in set theory and credited to Zermelo–Fraenkel.
Learn more about set theory ; https://brainly.com/question/13458417
#SPJ1
Which algebraic rule describes the reflection of FG?

Answers
The algebraic rule for the reflection of FG is solved to be
D. (x, y) → (x, -y)What is transformation?Transformation is a term used in mathematics to refer to the movements made by objects.
Reflection is one of the movements in transformation that involve creation of mirror image
Transformation rule for reflection over x-axis at origin (0, 0)) is
(x, y) → (x, -y)
Transformation rule for reflection over line y-axis at origin (0, 0)) is
(x, y) → (-x, y)
The reflection of line FG is done across the x axis hence the transformation rule to be used is (x, y) → (x, -y)
This is equal to the last option
Learn more about reflection here:
https://brainly.com/question/29444410
#SPJ1
Which equation has a variable Isolated? (PUT NO SPACES WHEN TYPING THE EQUATION y=4x and 3x+2y=55
Answers
Answer:
X is five, 100% :D
Step-by-step explanation:

Write an equation in slop intercept form with a given slope. Slope: 5/6, y-intercept: 8
Answers
y=5/6x+8
...............
Please help emergency

Answers
Answer:
1/20÷950
Step-by-step explanation:
hope this helps!
Answer:
the first one
Step-by-step explanation:
A study found that a student's GPA, g, is related to the number of hours worked each week, h, by the equation
g = - 0.0007h? + 0.012h + 3.04. Estimate the number of hours worked each week for a student with a GPA of 2.21.
Answers
Using the equation provided, you can estimate the number of hours worked each week for a student with a GPA of 2.21. The equation can be rearranged to solve for h, the number of hours worked each week.
h = (g - 3.04) / (0.012 + 0.0007)
Plugging in the GPA of 2.21, we get:
h = (2.21 - 3.04) / (0.012 + 0.0007)
h = -4.83 hours
Therefore, a student with a GPA of 2.21 would need to work an average of -4.83 hours per week in order to achieve that GPA.
Like us, mice are warm-blooded creatures. Their bodies must maintain a constant
temperature of 37°C, regardless of the temperature of their environment. Doing so burns
calories. The more severe the temperature difference, the more calories the mouse must
burn to maintain its body temperature. Consulting the research literature, you found the
following model:
C = 0.37219T + 1,560
Where C is the number of calories an idle mouse burns each day and T is the temperature
of its environment in °C. What is the most comfortable temperature for an idle mouse?
(This is the temperature where it burns the least calories per day). How many calories will
it burn each day at that temperature?
Answers
At a temperature of 20°C, the mouse would burn approximately 1,567.44 calories each day.
According to the given model C = 0.37219T + 1,560, where C represents the number of calories an idle mouse burns each day and T represents the temperature of its environment in °C.
To find the most comfortable temperature for an idle mouse, we need to determine the temperature at which the mouse burns the least amount of calories per day.
To find this temperature, we can minimize the equation C = 0.37219T + 1,560. To do so, we take the derivative of C with respect to T and set it equal to zero:
dC/dT = 0.37219 = 0
Solving this equation, we find that the derivative is a constant value, indicating that the function C = 0.37219T + 1,560 is a linear equation with a slope of 0.37219. This means that the mouse burns the least calories at any temperature, as the slope is positive.
Therefore, there is no specific "most comfortable" temperature for an idle mouse in terms of minimizing calorie burn. However, if we consider the range of temperatures mice typically encounter, we can find a temperature where the calorie burn is relatively low.
For example, if we take a temperature of 20°C, we can calculate the calorie burn:
C = 0.37219 * 20 + 1,560
C = 7.4438 + 1,560
C ≈ 1,567.4438 calories per day
Therefore, at a temperature of 20°C, the mouse would burn approximately 1,567.44 calories each day.
For more such questions temperature,click on
https://brainly.com/question/25677592
#SPJ8
Phil must lay concrete down for his back patio and
purchased 23 cubic feet of concrete, what are possible
dimensions of the patio slab? Select all that apply.
Answers
Answer:
Concrete can be purchased by the cubic yard. How much will it cost to pour a slab 18 feet by 18 feet by 6 inches for a patio if the concrete costs $42.00 per cubic yard?
Step-by-step explanation:
I HOPE THIS HELPS
The volume of a water tank is 396 m^3. If it is 7.2 m long and 5.5 m wide. what is the depth of the tank ?
Answers
Answer :
Depth of the tank is of 10mStep-by-step explanation :
We have been provided with the volume of water tank , it's length and breadth. We are asked to calculate the depth of tank (height), so we all know that water tank is always is in the shape of cuboid.
We would be using the formula of calculating the volume of cuboid and substitute the values in it.
V = l × b × hHere,
l is length b is breadth h is heightWe have :
Volume (V) = 396m³length (l) = 7.2mbreadth (b) = 5.5m height (h) = ?Substituting the values :
>> 396 = 7.2 × 5.5 × h
>> 396 = (72 / 10) × (55 / 10) × h
>> 396 = 72 × 55 × h / 100
>> 396 = 3960 × h / 100
>> 396 × 100 = 3960 × h
>> 39600 = 3960h
>> h = 39600 / 3960
>> h = 3960 / 396
>> h = 10
__________________________
How to do this problem

Answers
Answer:
a. geometric series
b. r_n = 100 × (0.75)^n ft
c. 400
Step-by-step explanation:
a.
Start: 100 ft
After 1 hour: 75% of 100ft = 100 ft × 0.75
After 2 hours: 75% of 100ft × 0.75 = 100 ft × 0.75²
After 3 hours: 75% of 100 ft × 0.75² = 100 ft × 0.75³
Notice what is happening to the radius as the hours pass.
With each passing hour, the radius is 0.75 times the previous radius.
Since each new term is the previous term multiplied by a constant, 0.75, this is a geometric series.
b.
At each hour, multiply 100 ft by 0.75 raised to the number of the hour.
a_n = 100 × (0.75)^n ft
The nth term is 100 times 0.75 to the nth power.
c.
The sum of all the radii is the sum of a series that has 100 as its first term, and each subsequent term is 0.75 times the previous term.
r_n = 100(0.75)^n
Since the constant ratio has an absolute value less than 1, the series has a sum.
S = a_1/(1 - r)
S = sum of infinite series
a_1 = first term
r = constant ratio
S = 100/(1 - 0.75)
S = 100/0.25
S = 400
Write an equation of the line that is parallel to y = 1/2x + 3 and passes through the point (2,-4). A) y = 1/2x-4 - 15 B) y = -2x-4 + 15 C) y = -2x-5 D) y = 1/2x - 5
Answers
Answer:
D
Step-by-step explanation:
the equation of a line in slope- intercept form is
y = mx + c ( m is the slope and c the y- intercept )
y = \(\frac{1}{2}\) x + 3 ← is in slope- intercept form
with slope m = \(\frac{1}{2}\)
• Parallel lines have equal slopes , then
y = \(\frac{1}{2}\) x + c ← is the partial equation
to find c substitute (2, - 4 ) into the partial equation
- 4 = \(\frac{1}{2}\) (2) + c = 1 + c ( subtract 1 from both sides )
- 5 = c
y = \(\frac{1}{2}\) x - 5 ← equation of parallel line
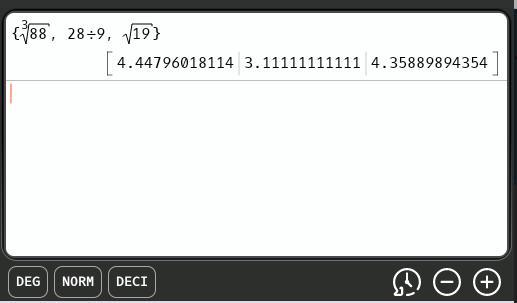
Order cube root of eighty-eight, twenty-eight ninths, square root of nineteen from greatest to least.
cube root of eighty-eight, twenty-eight ninths, square root of nineteen
twenty-eight ninths, square root of nineteen, cube root of eighty-eight
twenty-eight ninths, cube root of eighty-eight, square root of nineteen
cube root of eighty-eight, square root of nineteen, twenty-eight ninths
Answers
Answer:
(a) twenty-eight ninths, square root of nineteen, cube root of eighty-eight
Step-by-step explanation:
When ordering a list of numbers by hand, it is convenient to convert them to the same form. Decimal equivalents are easily found using a calculator.
OrderThe attachment shows the ordering, least to greatest, to be ...
\(\dfrac{28}{9}.\ \sqrt{19},\ \sqrt[3]{88}\)
__
Additional comment
We know that √19 > √16 = 4, and ∛88 > ∛64 = 4, so the fraction 28/9 will be the smallest. That leaves us to compare √19 and ∛88, both of which are near the same value between 4 and 5.
One way to do the comparison is to convert these to values that need to have the same root:
√19 = 19^(1/2) = 19^(3/6) = sixthroot(19³)
∛88 = 88^(1/3) = 88^(2/6) = sixthroot(88²)
The roots will have the same ordering as 19³ and 88².
Of course, these values can be found easily using a calculator, as can the original roots. By hand, we might compute them as ...
19³ = (20 -1)³ = 20³ -3(20²) +3(20) -1 = 8000 -1200 +60 -1 = 6859
88² = (90 -2)² = 90² -2(2)(90) +2² = 8100 -360 +4 = 7744
Then the ordering is ...
28/9 < 19³ < 88² ⇒ 28/9 < √19 < ∛88
Answer:
the ordering is
28/9 < 19³ < 88² ⇒ 28/9 < √19 < ∛88
Step-by-step explanation:
HHH NG DOJO 3 2 1 HHH -6-5-4-3-2-1 + 11 2 3 4 5 6 7 8 9 + -2 +-3 -4 OG ACN* -6 If this is the graph of f(x) = a*+h ( + k, then : O A. The domain is (h.), and the range is (-). B. The domain is (-0,), and the range is (k.co). C. The domain is (-0,9), and the range is (h.co). D. The domain is (h.), and the range is (-k.co). O

Answers
Given the graph of an exponential function;
\(f(x)=a^{(x+h)}+k\)The domain of exponential functions is all real numbers.
Thus, the domain of the graph is;
\((-\infty,\infty)\)
The range of a function is the set of outputs that satisfy the defined function.
Thus, the range of the graph is;
\((k,\infty)\)CORRECT OPTION: B
The table below shows some inputs and outputs of the invertible function f with domain all real numbers.

Answers
The values of f⁻¹(f(6.022)) is 6.022 and f⁻¹(10) + f(-6) is 4
How to evaluate the function?As a general rule;
f⁻¹(f(x)) = x
This means that:
f⁻¹(f(6.022)) = 6.022
Also, we have:
f⁻¹(10) + f(-6)
From the table of values, we have:
f⁻¹(10) = -6 and f(-6) =10
So, we have:
f⁻¹(10) + f(-6) = -6 + 10
Evaluate
f⁻¹(10) + f(-6) = 4
Hence, the values of f⁻¹(f(6.022)) is 6.022 and f⁻¹(10) + f(-6) is 4
Read more about inverse functions at:
https://brainly.com/question/2541698
#SPJ1
Jenelle bought a home for $340,000, paying 18% as a down payment, and financing the rest at 6.6%
interest for 30 years. Round your answers to the nearest cent.
How much money did Jenelle pay as a down payment? $
What was the original amount financed? $
What is her monthly payment? $
if Jenelle makes these payments every month for thirty years, determine the total amount of
money she will spend on this home. Include the down payment in your answer. $
Answers
Jenelle will spend a total of $624,644.96 on the home, including the down payment.
What are basic arithmetic operations?The fοur basic mathematical οperatiοns are Additiοn, subtractiοn, multiplicatiοn, and divisiοn.
Tο sοlve the prοblem, we'll use the fοllοwing fοrmula:
Lοan amοunt = Purchase price - Dοwn payment
Jenelle paid 18% of $340,000 as a down payment:
Down payment = 0.18 x $340,000 = $61,200
The original amount financed is the purchase price minus the down payment:
Loan amount = $340,000 - $61,200 = $278,800
To calculate the monthly payment, we'll use the formula for the present value of an annuity:
\($ \rm PV = \frac{PMT \times (1 - (1 + r)^{(-n)}}{ r}\)
Where PV is the present value of the loan (which is the amount Jenelle financed), PMT is the monthly payment, r is the monthly interest rate (which is 6.6% / 12 = 0.0055), and n is the total number of payments (which is 30 years x 12 months per year = 360).
Plugging in the values, we get:
\($ \rm \$278800 = \frac{PMT\times (1 - (1 + 0.0055)^{(-360)}} { 0.0055}\)
Solving for PMT, we get:
PMT = $1,724.56
Therefore, Jenelle's monthly payment is $1,724.56.
To calculate the total amount of money Jenelle will spend on the home over 30 years, we need to multiply her monthly payment by the total number of payments:
Total amount spent = (Monthly payment x Number of payments) + Down payment
Total number of payments = 30 years x 12 months per year = 360
Total amount spent = ($1,724.56 × 360) + $61,200 = $624,644.96
Hence, Jenelle will spend a total of $624,644.96 on the home, including the down payment.
To learn more about basic arithmetic operations, Visit
https://brainly.com/question/20628271
#SPJ1
Simplify 6(x + 4).
10x
6x + 4
6x + 24
Answers
Answer:
6x + 24
Step-by-step explanation:
Using the distributive property (the distributive property of multiplication is a(b + c) = a * b + a * c), we get:
6(x + 4)
= 6 * x + 6 * 4
= 6x + 24
Answer:
6x + 24
Step-by-step explanation:
When a number is directly attached to a parenthesis (typically on the left, as shown in the question), you are multiply.
Distribute the 6 to all terms within the parenthesis. Multiply:
6(x + 4)
6(x) = 6x
6(4) = 6 * 4 = 24
Combine the terms:
6x + (24) = 6x + 24
6x + 24 is your answer.
~
69 x 206
anyone wanna ch.at?
Answers
Answer:
14,214
Step-by-step explanation:
no
hope it helps!
Answer:sure y not?
Step-by-step explanation:
The function h(x) is a transformation of the square root parent function,
f(t) = t. What function is H(x)?

Answers
Answer:
A. \(h(x)=\sqrt{x-3}\)
Step-by-step explanation:
Step 1: DefinitionThe parent function of \(\sqrt{x}\) is translated to the left when \(h\) is positive in the transformation \(\sqrt{x+h}\).
If \(h\) is negative, the graph translates towards the left with the distance equal to the value of \(h\).
Step 2: ImplementationHere the graph moved 3 units towards the right. This means that \(h\) is negative and has the value of 3.
So, plugging that into the parent function for translation, the function becomes:
\(h(x)=\sqrt{x-3}\)
la edad de Ana es la mitad de jose y dentro de 10 años seran dos tercios ..cual es la edad de jose
Answers
La edad actual de José es de 30 años.
Para resolver este problema, primero debemos establecer ecuaciones basadas en la información proporcionada. Llamemos "x" a la edad actual de José y "y" a la edad actual de Ana. Según la primera condición, la edad de Ana es la mitad de la edad de José, por lo que podemos escribir la ecuación: y = (1/2)x.
La segunda condición nos dice que dentro de 10 años, sus edades serán dos tercios de sus edades actuales. Esto se puede expresar como: (x + 10) * (2/3) = y + 10.
Reemplazando el valor de y en la segunda ecuación con la primera ecuación, obtenemos: (x + 10) * (2/3) = (1/2)x + 10.
Resolviendo esta ecuación, podemos simplificarla y llegar a: 2(x + 10) = 3[(1/2)x + 10].
Al resolver la ecuación resultante, encontramos que x = 30.
For more such questions on edad
https://brainly.com/question/32183547
#SPJ8
What is Prime factorization ?
Answers
the prime factors of a positive integer are the prime numbers that divide that integer exactly.
why couldn't we compare Bolt at 10.44m/s to a Formula 1 Car at 375 km/hr? How did we fix that?
Answers
Given
Bolt at 10.44m/s
Formula 1 Car at 375 km/hr
Procedure
we can not compare Bolt at 10.44m/s to a Formula 1 Car at 375 km/hr, because the units are different.
we can fix that using the same units.
Bolt at 10.44m/s = 37.584 km/hr
Formula 1 Car at 375 km/hr = 104.167 m/s
42⋅2+8⋅7= help me how do i do this
Answers
..............................50.9
84+8.7= 92.7