Use the following set definitions to specify each set in roster notation. Except where noted, express elements of Cartesian products as strings. A = {a} B = {b, c} C = {a, b, d}
(a) A × (B ∪ C) Solution {aa, ab, ac, ad}
(b) A × (B ∩ C)
(c) (A × B) ∪ (A × C)
(d) (A × B) ∩ (A × C)
Answers
Answer:
Step-by-step explanation:
Given the set notations A = {a} B = {b, c} C = {a, b, d}
BUC = {a, b, c, d}
B∩C = {b}
a) A × (BUC) = {aa, ab, ac, ad}
b) A × (B ∩ C) = {ab}
c) (A × B) ∪ (A × C)
A × B = {ab, ac} and A × C = {aa, ab, ad}
(A × B) ∪ (A × C) = {aa, ab, ac, ad}
d) For (A × B) ∩ (A × C)
(A × B) ∩ (A × C) = {ab}
Note that the union (U) of two sets is the combination of all the elements in both sets while the intersection (∩)of two sets is the common elements that are found in both sets.
The Cartesian product of two sets is derived by mapping each of the element in the first set with all the element in the other set. It is denoted by the multiplication sign.
Related Questions
There are 4 consecutive even integers that add up to 100. What is the least of the 4 integers?
Answers
The least among all 4 integers such that they sum up to 100 will be 22.
What is an integer?An integer is a whole number irrespective of the sign that the integer is all whole numbers that are going from 0 to infinite or 0 to minus infinite.
Integer; ....-2 , -1 , 0 , 1 , 2 , .....
Integers are non-decimal numbers and all integers are rational numbers.
Suppose the first integer is x.
The next three digits will be, x + 2, x + 4, and x + 6 correspondings.
Sum x + x + 2 + x + 4 + x + 6 = 100
(x + x + x + x) + (2 + 4 + 6) = 100
4x + 12 = 100
4x = 88
x = 22
Hence"The smallest of the four integers that add up to 100 is 22".
To learn more about integers,
brainly.com/question/1768254
#SPJ1
Given the points below, find XY. Round to
the nearest hundredth.
X(-9, 2) and Y(5, -4)
Answers
The distance between X(-9,2) and Y(5,-4) is 15.23 units.
The distance formula states that if there are 2 points A(x1, y1) and B(x2, y2), then the distance between the two points is given by the formula-
\(\sqrt{(x1-x2)^{2} + (y1-y2)^{2} }\)
Here, we are given that there are 2 points- X(-9, 2) and Y(5, -4)
So here we can say that,
x1 = -9, y1 = 2
and x2 = 5, y2 = -4
Now, plugging in the values given above in the distance formula we will find XY as follows-
XY = \(\sqrt{(-9-5)^{2} + (5+4)^{2} }\)
XY = \(\sqrt{(-14)^{2} + (9)^{2} }\)
XY = \(\sqrt{196+ 81 }\)
XY = \(\sqrt{277 }\)
The square root of 277 is approximately 15.23.
Thus, XY = 15.23
Therefore the value of XY to the nearest hundredth is 15.23 units.
Learn more about distance between two points here-
brainly.com/question/17962414
For thousands of years, gold has been considered one of the Earth's most precious metals. One hundred percent pure gold is 24-karat gold, which is
too soft to be made into jewelry. Most gold jewelry is 14-karat gold, approximately 58% gold. If 18-karat gold is 75% gold and 12-karat gold is 50% gold,
how much of each should be used to make a 14-karat gold bracelet weighing 300 grams?
How many grams of 18-karat gold needs to be used to make the bracelet?
Answers
Tasha used the pattern in the table to find the value of 4 Superscript negative 4.
Powers of 4
Value
4 squared
16
4 Superscript 1
4
4 Superscript 0
1
4 Superscript negative 1
One-fourth
4 Superscript negative 2
StartFraction 1 Over 16 EndFraction
She used these steps.
Step 1 Find a pattern in the table.
The pattern is to divide the previous value by 4 when the exponent decreases by 1.
Step 2 Find the value of 4 Superscript negative 3.
4 Superscript negative 3 = StartFraction 1 Over 16 EndFraction divided by 4 = StartFraction 1 Over 16 EndFraction times one-fourth = StartFraction 1 Over 64 EndFraction
Step 3 Find the value of 4 Superscript negative 4.
4 Superscript negative 4 = StartFraction 1 Over 64 EndFraction divided by 4 = StartFraction 1 Over 64 EndFraction times one-fourth = StartFraction 1 Over 256 EndFraction
Step 4 Rewrite the value for 4 Superscript negative 4.
StartFraction 1 Over 256 EndFraction = negative StartFraction 1 Over 4 Superscript negative 4 EndFraction
Answers
The value of 4 Superscript negative 4 is negative StartFraction 1 Over 4 Superscript negative 4 EndFraction.
In the given table, Tasha observed a pattern in the powers of 4. When the exponent decreases by 1, the previous value is divided by 4. Using this pattern, she determined the values for 4 squared, 4 Superscript 1, 4 Superscript 0, 4 Superscript negative 1, and 4 Superscript negative 2.
To find the value of 4 Superscript negative 3, she divided the previous value (StartFraction 1 Over 16 EndFraction) by 4, resulting in StartFraction 1 Over 64 EndFraction.
Similarly, for 4 Superscript negative 4, she divided the previous value (StartFraction 1 Over 64 EndFraction) by 4, yielding StartFraction 1 Over 256 EndFraction.
Finally, to rewrite the value for 4 Superscript negative 4, she expressed it as negative StartFraction 1 Over 4 Superscript negative 4 EndFraction.
Therefore, the value of 4 Superscript negative 4 is negative StartFraction 1 Over 4 Superscript negative 4 EndFraction, which simplifies to StartFraction 1 Over 256 EndFraction
For more such answers on Superscript
https://brainly.com/question/29971585
#SPJ8
One in 1000 adults is afflicted with a rare disease forwhich a diagnostic test has been developed. The test is such,that when an individual has the disease, a positive result willoccur 98% of the time, while an individual without the disease willshow a positive result only 1% of the time. If a randomlyselected individual is tested and the result is positive, what isthe probability that the individual has the disease?
Answers
Answer:
0.0893
Step-by-step explanation:
Let A be the event that the individual has the disease
Let Aⁿ be the event that the individual doesn't have the disease
Let B be the event of a positive result showing.
Now,
We are told One in 1000 adults is afflicted with the disease.
Thus;
P(A) = 1/1000 = 0.001
P(Aⁿ) = 1 - 0.001 = 0.999
Also,we are told that when an individual has the disease, a positive result will occur 98% of the time.
Thus;
P(A|B) = 98% = 0.98
Also, we are told that an individual without the disease will show a positive result only 1% of the time. Thus;
P(Aⁿ|B) = 1% = 0.01
Now, from fundamental rule, let's find P(B). Thus;
P(B) = [P(A|B) × P(A)] + [P(Aⁿ|B) × P(Aⁿ)]
P(B) = (0.98 × 0.001) + (0.01 × 0.999)
P(B) = 0.01097
Now, from Baye's theorem, If a randomly selected individual is tested and the result is positive, the probability that the individual has the disease is given by;
P(A|B) = [P(A|B) × P(A)]/P(B)
P(A|B) = (0.98 × 0.001)/0.01097
P(A|B) = 0.0893
Calc II Question
Find the volume of the solid obtained by rotating the region bonded bt the given curves about the specified line.
Y = e^-x
Y = 1
X = 2
About the Y = 2
Answers
Answer:
\(\displaystyle \frac{\pi(5e^4+8e^2-1)}{2e^4}\approx9.526\)
Step-by-step explanation:
This can be solved with either the washer (easier) or the shell method (harder). For the disk/washer method, the slice is perpendicular to the axis of revolution, whereas, for the shell method, the slice is parallel to the axis of revolution. I'll show how to do it with both:
Shell Method (Horizontal Axis)
\(\displaystyle V=2\pi\int^d_cr(y)h(y)\,dy\)
Radius: \(r(y)=2-y\) (distance from y=2 to x-axis)
Height: \(h(y)=2-(-\ln y)=2+\ln y\) (\(y=e^{-x}\) is the same as \(x=-\ln y\))
Bounds: \([c,d]=[e^{-2},1]\) (plugging x-bounds in gets you this)
Plugging in our integral, we get:
\(\displaystyle V=2\pi\int^1_{e^{-2}}(2-y)(2+\ln y)\,dy=\frac{\pi(5e^4+8e^2-1)}{2e^4}\approx9.526\)
Washer Method (Parallel to x-axis)
\(\displaystyle V=\pi\int^b_a\biggr(R(x)^2-r(x)^2\biggr)\,dx\)
Outer Radius: \(R(x)=2-e^{-x}\) (distance between \(y=2\) and \(y=e^{-x}\))
Inner Radius: \(r(x)=2-1=1\) (distance between \(y=2\) and \(y=1\))
Bounds: \([a,b]=[0,2]\)
Plugging in our integral, we get:
\(\displaystyle V=\pi\int^2_0\biggr((2-e^{-x})^2-1^2\biggr)\,dx\\\\V=\pi\int^2_0\biggr((4-4e^{-x}+e^{-2x})-1\biggr)\,dx\\\\V=\pi\int^2_0(3-4e^{-x}+e^{-2x})\,dx\\\\V=\pi\biggr(3x+4e^{-x}-\frac{1}{2}e^{-2x}\biggr)\biggr|^2_0\\\\V=\pi\biggr[\biggr(3(2)+4e^{-2}-\frac{1}{2}e^{-2(2)}\biggr)-\biggr(3(0)+4e^{-0}-\frac{1}{2}e^{-2(0)}\biggr)\biggr]\\\\V=\pi\biggr[\biggr(6+4e^{-2}-\frac{1}{2}e^{-4}\biggr)-\biggr(4-\frac{1}{2}\biggr)\biggr]\)
\(\displaystyle V=\pi\biggr[\biggr(6+4e^{-2}-\frac{1}{2}e^{-4}\biggr)-\frac{7}{2}\biggr]\\\\V=\pi\biggr(\frac{5}{2}+4e^{-2}-\frac{1}{2}e^{-4}\biggr)\\\\V=\pi\biggr(\frac{5}{2}+\frac{4}{e^2}-\frac{1}{2e^4}\biggr)\\\\V=\pi\biggr(\frac{5e^4}{2e^4}+\frac{8e^2}{2e^4}-\frac{1}{2e^4}\biggr)\\\\V=\pi\biggr(\frac{5e^4+8e^2-1}{2e^4}\biggr)\\\\V=\frac{\pi(5e^4+8e^2-1)}{2e^4}\approx9.526\)
Use your best judgment when deciding on what method you use when visualizing the solid, but I hope this helped!

The number of subscribers to a web service is growing exponentially. If there were 100,000 subscribers initially and it grows by 2.4% per month, how many subscribers will there be after a year? Round your answer to the nearest whole number of subscribers.
Answers
Answer:
280,000
Step-by-step explanation:
Solve
Given: 100,000 subscribers increases by 2.4% per month
To find: After a year, how much will that be?
First step:
Find the increase of the subscribers per month
100,000 of 2.4%
Set up an equation
2.4/100 × 100,000/1
Cross multiply, cancel zeros in both 100,000 and 100. Which is equal to:
2.4/1 x 1,000/1 =
2,400
Second step: If it increases per month,
then to find the year, find out how many months is in a year:
12 months = 1 year
Now that has been figured out, multiply the result by the result in the first step:
12 × 2400 = 28.800
Therefore, the number of subscribers will be after a year
what is 6 10th in simplest form
Answers
Answer:
3/5ths
Yw :)
Answer:
3 / 5 (three - fifths)
Step-by-step explanation:
6 / 10 =
Divide both the top and bottom by 2.
3 / 5
Because 3 and 5 are prime numbers (5 can only be divided by 1 and 5, and 3 can only be divided by 1 and 3), this is the most simplified form.
You are preparing to buy a house. Your monthly gross income is $3,200. a. What is the maximum amount you can finance (mortgage)? (4 points)
Answers
The maximum amount you can finance is $896.
We are given that;
The monthly gross income = $3,200
Now,
28% of your gross monthly income on your mortgage, including taxes and insurance
The percentage = 28%
3200* 28/100
=32*28
=896
Therefore, by percentage the answer will be $896.
Learn more about percent here:
https://brainly.com/question/11549320
#SPJ1
Identify the solid formed by rotating the two-dimensional shape about the line.
Select Choice
pls help!!!!!

Answers
Answer:
Got you bro
Step-by-step explanation:
The two-dimensional shape appears to be a semi-circle, and it is being rotated about a line to form a three-dimensional shape. The resulting shape is a sphere.
Answer:
Step-by-step explanation:
The two-dimensional shape appears to be a semi-circle, and it is being rotated about a line to form a three-dimensional shape.
The resulting shape is a sphere.
35 POINTS WILL GIVE BRAINLYEST 5 QUESTIONS




Answers
4) If a shoe of size 9.5 is added to the data, the way the median would change is that; The median will increase to 7
5) If a value of 50° is added, the way that the median will change is that; The Median decreased to 77°
6) If 101° is added, then ; Mean increases to 82°
How to find the measure of central tendency?4) Arranging the shoe sizes from least to greatest is;
5, 5.5, 6, 6.5, 6.5, 7, 7.5, 8, 8, 8.5
The median here will be; (7 + 6.5)/2 = 6.75
If a size of shoe of 9.5 is added, the sizes will be arranged as;
5, 5.5, 6, 6.5, 6.5, 7, 7.5, 8, 8, 8.5, 9.5
The median will increase to 7
5) Arranging the average high temperatures from least to greatest is;
57, 58, 61, 66, 71, 77, 82, 91, 95, 100, 102, 105
The median here will be; (77 + 82)/2 = 78.5
If we add 50° to the values, the median is now;
Median = 77
Median decreased to 77°
6) 57, 58, 61, 66, 71, 77, 82, 91, 95, 100, 102, 105
The mean is; (57 + 58 + 61 + 66 + 71 + 77 + 82 + 91 + 95 + 100 + 102 + 105)/12 = 80.42
If 101° is added, mean = (965 + 101)/13 = 82
Mean increases to 82°
Read more about Measure of Central Tendency at; https://brainly.com/question/17631693
#SPJ1
Enter the number that belongs in the green box
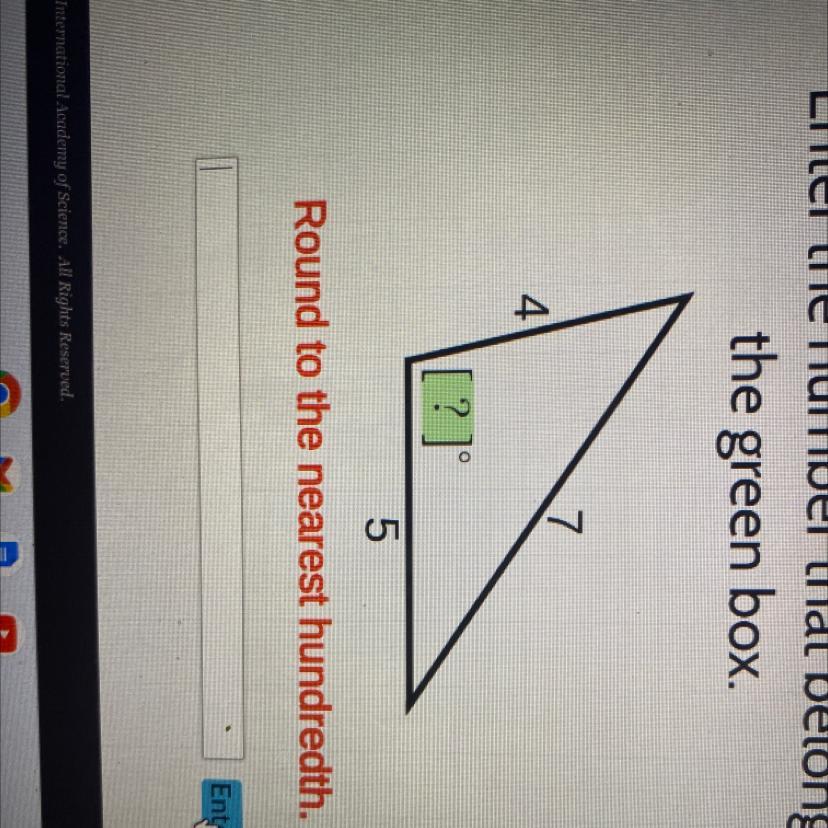
Answers
The angle between the sides measuring 4 and 5 in the obtuse triangle is approximately 101.54 degrees.
To find the measure of the angle between the sides measuring 4 and 5 in an obtuse triangle with side lengths 4, 5, and 7, we can use the Law of Cosines. The Law of Cosines states that in a triangle with side lengths a, b, and c, and an angle opposite to side c, the following equation holds:
\(c^2 = a^2 + b^2 - 2ab*cos(C)\)
In this case, we have side lengths a = 4, b = 5, and c = 7. We want to find the angle C, which is opposite to side c. Substituting these values into the Law of Cosines, we get:
\(7^2 = 4^2 + 5^2\)- 2(4)(5)*cos(C)
49 = 16 + 25 - 40*cos(C)
49 = 41 - 40*cos(C)
40*cos(C) = 41 - 49
40*cos(C) = -8
cos(C) = -8/40
cos(C) = -0.2
To find the measure of angle C, we can take the inverse cosine (arccos) of -0.2:
C = arccos(-0.2)
Using a calculator, we find that C ≈ 101.54 degrees.
Therefore, the measure of the angle between the sides measuring 4 and 5 in the obtuse triangle is approximately 101.54 degrees.
For more such information on: angle
https://brainly.com/question/25716982
#SPJ8
Please if you know the answer tell me it and the steps also thank you.

Answers
Step-by-step explanation: Well to begin, you take 15$ and multiply it by 4, since he wants to buy 4 of those tickets, which is 60$. Then, take the 10$ and multiply it by 2 since he wants 2 of those tickets, which is 20$, you then apply 10% to 60 and 20 by taking 10 percent of 60, then adding it to 60 once have that, which is 66, you take the 3% and find 3% of 66, then add the answer of that to 66, which is 67.98$, you then do the same thing to the 20$.
Sorry if this didnt help, im sure it didnt because im a very bad explainer, but i tried..
The finishing times for a race happen to be normally distributed with a mean of 10.2 seconds and a standard deviation of 1.4 seconds. Find the cut off score for the top 10%. Interpret this result.
Answers
Using the normal distribution, it is found that the cut off score for the top 10% is of 8.4 seconds. It means that a person with a time of 8.4 seconds or lower is in the faster 10% of runners.
In a normal distribution with mean \(\mu\) and standard deviation \(\sigma\), the z-score of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
It measures how many standard deviations the measure is from the mean. After finding the z-score, we look at the z-score table and find the p-value associated with this z-score, which is the percentile of X.In this problem:
Mean of 10.2 seconds, hence \(\mu = 10.2\)Standard deviation of 1.4 seconds, hence \(\sigma = 1.4\).The lower the times, the faster the runners are, hence, the cut off score for the top 10% is the 10th percentile, which is X when Z has a p-value of 0.1, so X when Z = -1.28.
\(Z = \frac{X - \mu}{\sigma}\)
\(-1.28 = \frac{X - 10.2}{1.4}\)
\(X - 10.2 = -1.28(1.4)\)
\(X = 8.4\)
The cut off score for the top 10% is of 8.4 seconds. It means that a person with a time of 8.4 seconds or lower is in the faster 10% of runners.
A similar problem is given at https://brainly.com/question/24663213
(2.8•10^8)(1.9•10^4)
Answers
Answer: 5.32 × 10^12
Step-by-step explanation:
This is a question relating to indices. In indices, we add the power given for question relating to multiplication. Hence, this will be:
= (2.8•10^8)(1.9•10^4)
= (2.8 × 1.9) × 10^8+4
= 5.32 × 10^12
Therefore, the answer to the question will be 5.32 × 10^12.
If f(x)=3x² -2 and g(x) = 2x+4, find (f - g)(x) pretty please?

Answers
Answer:
3x^2-2x-6
Step-by-step explanation:
So first i paid attention in class
second apply to my homework
third step apply too your
<33 ur welcome lol
13-2x=4x+7 I’m being asked how to solve this
Answers
Answer:
Step-by-step explanation:
13-2x=4x+7 -2x+13=4x+7 (-2x+13)+(-13-4x)=(4x+7)+(-13-4x) -2x+13-4x-13=4x+7-13-4x
-2x-4x+13-13=4x-4x+7-13 -6x=-6 6x/6=6/6 x=1
3. two dice are thrown. consider the sample space with 36 (equally likely) outcomes. let sj be the event that the total of the values which come up on the dice is j. find p(s2), p(s3), p(s4), p(s5), p(s6), p(s7), and p(s8); in doing so, show all the outcomes in each event being considered.
Answers
The value of the probability p(s2) is 1.36, p(s3) is 1/18, p(s4) is 1/12, p(s5) is 1/9, p(s6) is 5/36, p(s7) is 1/6, and p(s8) 5/36
The sample space for this problem can be represented as all the possible outcomes when two dice are thrown.
Each die has six sides with numbers 1 through 6, so there are 6 x 6 = 36 possible outcomes. We can represent each outcome as a pair of numbers (i, j) where i is the number on the first die and j is the number on the second die.
Now, we want to find the probability of getting a certain total when the two dice are thrown. We can define an event Sj as the event where the total of the values on the dice is j.
To calculate the probability of each event, we need to count the number of outcomes that belong to each event, and divide by the total number of outcomes (which is 36).
Let's start with S2. The only outcome that belongs to this event is (1, 1), so the probability of getting a total of 2 is 1/36.
For S3, we can get a total of 3 in two ways: (1, 2) and (2, 1). So the probability of getting a total of 3 is 2/36 or 1/18.
For S4, we can get a total of 4 in three ways: (1, 3), (2, 2), and (3, 1). So the probability of getting a total of 4 is 3/36 or 1/12.
For S5, we can get a total of 5 in four ways: (1, 4), (2, 3), (3, 2), and (4, 1). So the probability of getting a total of 5 is 4/36 or 1/9.
For S6, we can get a total of 6 in five ways: (1, 5), (2, 4), (3, 3), (4, 2), and (5, 1). So the probability of getting a total of 6 is 5/36.
For S7, we can get a total of 7 in six ways: (1, 6), (2, 5), (3, 4), (4, 3), (5, 2), and (6, 1). So the probability of getting a total of 7 is 6/36 or 1/6.
Finally, for S8, we can get a total of 8 in five ways: (2, 6), (3, 5), (4, 4), (5, 3), and (6, 2). So the probability of getting a total of 8 is 5/36.
To know more about probability here.
https://brainly.com/question/11234923
#SPJ4
Which of the following is false regarding number sets

Answers
Answer:
D
Step-by-step explanation:
just took a random guess
Solve for x: 1 < x + 3 < 4
4 > x > 7
4 < x < 7
−2 > x > 1
−2 < x < 1
100 points!!!
Answers
Answer:
Solve for x: x < 1
Step-by-step explanation:
♡♡♡♡♡♡♡♡♡♡♡♡♡♡♡♡♡♡♡♡♡♡♡♡♡♡♡♡♡♡♡♡♡♡♡♡♡

HELP ME!!!!!
Solve. −n/2 + 3/8 = −6 7/8 Enter your answer as a mixed number in simplest form in the box.
Answers
Your answer should be n=14 1/2. Hope this helped.
Using a directrix of y = 5 and a focus of (4, 1), what quadratic function is created?
HELP PLS
Answers
Answer:
(x-4)^2=-8(y-3)
This is a parabola.
Step-by-step explanation:
Since the directrix is horizontal, the parabola faces up or down. Since the focus is below the directix it faces down. This means p will be negative in the equation (x-h)^2=4p(y-k).
p also tells us the half the distance between the focus and the directrix. The distance between 1 and 5 is 4, so p=-2.
The vertex is half way point between focus (4,1) and directrix y=5.
So the vertex is (4, [1+5]/2 )= (4 ,6/2)=(4,3). This is (h,k) in our equation.
(x-h)^2=4p(y-k)
(x-4)^2=4×-2(y-3)
(x-4)^2=-8(y-3)
Which would most likely be graphed using a continuous graph? Check all that apply.
Answers
The items that would most likely be graphed using a continuous graph are:
total cost, c, of buying g pounds of broccoli.speed of a car, s, as it accelerates over time, t.total distance, d, that has been driven over time, tdecrease in outside temperature, F, one evening over time, t.What are explanation for the items?1. Total cost, c, of buying b cans of beans:
Cans of beans is the input, and the number of cans is a countable number, that is, 0, 1, 2, ..., so a discrete graph is used, and the option is not checked.2. Total cost, c, of buying g pounds of broccoli
Pounds can assume decimal values, so it is a continuous variable, and a continuous graph is used, and this option is checked.3. Speed of a car, s, as it accelerates over time, t:
Total distance, d, that has been driven over time, t
Decrease in outside temperature, F, one evening over time, t
Time can assume decimal values, like 0.5 seconds, 0.5 hours, so it is a continuous variable, and a continuous graph is used, and these options is checked.4. Number of stamps, s, needed to mail p postcards
The number of postcards is the input, and the number of postcards is a countable number, that is, 0, 1, 2, ..., so a discrete graph is used, and the option is not checked.Missing options "- total cost, c, of buying b cans of beans
- total cost, c, of buying g pounds of broccoli
- speed of a car, s, as it accelerates over time, t
- number of stamps, s, needed to mail p postcards
- total distance, d, that has been driven over time, t
- decrease in outside temperature, F, one evening over time, t
Read more about continuous graph
brainly.com/question/7717858
#SPJ1
.
At a meat packing plant in Green Bay, the owners want to begin a continuing education program so their 186 employees can get a college education online if they desire. The following table represents an incomplete picture of the results. Use the following two-way frequency table for the questions below:
Men Women Total
No College Credit 28 A B
Some College C D 81
College Graduate 15 22 E
Total 79 F 186
a. Fill in the missing data in the table for values A through F. Explain the strategies you used to get each answer.
b. Describe a few pieces of data in terms of joint relative frequency. Explain why these data are both joint and relative.
c. Explain a few ways we can summarize pieces of this table using conditional relative and marginal relative frequency.
d. Are the data independent or dependent? Why?
Answers
Answer:
a. To fill in the missing data in the table, we can use the information given in the table along with the fact that the total number of employees is 186.
For value A: Since the total number of employees with no college credit is 28, and the total number of men is 79, we can subtract the number of men with some college (C) and college graduates (15) from the total number of men to find the missing value A. So A = 79 - C - 15.
For value B: Since the total number of women is 186, we can subtract the number of women with some college (D) and college graduates (22) from the total number of women to find the missing value B. So B = 186 - D - 22.
For value C: Since the total number of employees with some college is 81, and we have already determined the values A and D, we can subtract A and D from the total number of employees with some college to find the missing value C. So C = 81 - A - D.
For value D: Similarly, we can subtract B and E from the total number of women to find the missing value D. So D = 186 - B - E.
For value E: Since the total number of college graduates is 37 (15 men + 22 women), we can subtract the number of college graduates among men (15) from the total to find the missing value E. So E = 37 - 15.
For value F: Since the total number of employees is 186, we can subtract the total number of men (79) from the total to find the missing value F. So F = 186 - 79.
b. Joint relative frequency refers to the proportion of individuals that fall into a particular combination of categories. For example, the joint relative frequency of men with no college credit is the number of men with no college credit divided by the total number of employees (28/186). These data are joint and relative because they represent the proportion of individuals in a specific category combination relative to the total population.
c. To summarize the data using conditional relative frequency, we can calculate the proportion of individuals in each category given a specific condition. For example, we can calculate the conditional relative frequency of women who are college graduates by dividing the number of women who are college graduates (22) by the total number of women (186). Similarly, we can calculate the conditional relative frequency of men with some college by dividing the number of men with some college (C) by the total number of men (79).
To summarize the data using marginal relative frequency, we can calculate the proportion of individuals in each category by dividing the number of individuals in that category by the total number of individuals. For example, we can calculate the marginal relative frequency of men by dividing the total number of men (79) by the total number of employees (186). Similarly, we can calculate the marginal relative frequency of college graduates by dividing the total number of college graduates (37) by the total number of employees (186).
d. The data in the table can be analyzed to determine if there is an association or relationship between the variables. If the values in the table change depending on the categories of the other variable, then the variables are dependent. In this case, the data is dependent because the number of individuals with certain educational levels (no college credit, some college, college graduate) varies based on their gender. For example, there are different proportions of men and women in each educational category, indicating a relationship between gender and education level.
Step-by-step explanation:
The missing values in the two-way frequency table are filled based on the given values and the composition of the table. The table represents joint relative frequency, which is the proportion of specific groups in the total population. We can summarize the data using marginal and conditional relative frequencies, and the data are considered dependent because an employee's education level depends on their gender.
Explanation:To fill in the missing values of the two-way frequency table, we need to use the given numbers and the rules of the two-way frequency table. Here are the strategies used for filling in the values for A through F:
A = Total number of women - Total number of women with some college and college graduate education (in this case A = F - D - 22, because we know the number of total women F and the number of women college graduates 22, but D is still unknown).B = Total number of employees - Total number of men - Total number of women (B = 186 - 79 - F).C = Total number of some college - Number of women with some college (C = 81 - D)D = Total number of some college - Number of men with some college (D = 81 - C).E = Total number of employees - Total of men and women with and without college (E = 186 - B - 81 - 37F = Total number of employees - Total number of men (F = 186 - 79).The table will also represent joint relative frequency because each cell represents the joint occurrence of two categories (gender and education level). For example, the number of male employees with no college credit (28) divided by the total number of employees (186) is a joint relative frequency.
We may summarize the table data using conditional relative frequency and marginal relative frequency. The marginal relative frequency is the total of each row or column divided by the grand total. The conditional relative frequency would be, for example, the proportion of women among those with no college credit.
The data are dependent because the education level depends on whether the employee is a man or a woman.
Learn more about Two-Way Frequency Tablehttps://brainly.com/question/16148316
#SPJ2
Which equation represents h(x)?
The table shows three functions and their output values
for different values of x.
0 h(x) =
g(x)
х
1
2
3
3
9
27
g(x)
18
21
24
h(x)
15
12
-3
O h(x) = 0
Oh(x) = f(x) - g(x)
Oh(x) = g(x) – f(x)
Answers
Answer: -01
Step-by-step explanation:
The correct equation for represents h (x) is,
⇒ h (x) = g (x) - h (x)
What is mean by Function?A relation between a set of inputs having one output each is called a function. and an expression, rule, or law that defines a relationship between one variable (the independent variable) and another variable (the dependent variable).
We have to given that;
The table shows three functions and their output values for different values of x.
Now, By the table;
f (x) = 3
g (x) = 18
h (x) = 15
Hence, We can formulate;
g (x) - f (x) = 18 - 3
= 15
= h (x)
Thus, The correct equation for represents h (x) is,
⇒ h (x) = g (x) - h (x)
Learn more about the function visit:
https://brainly.com/question/11624077
#SPJ7

A tank is full of water. Find the work required to pump the water out of the spout. (Use 9.8 m/s2 for g. Use 1000 kg/m3 as the density of water. Assume r = 6 m and h = 2 m.)
Answers
The work required to pump the water out of the spout is 70.9 * 10⁶ joules which is 71 M Joules approx.
Let the spherical tank be divided into a series of horizontal disks.
Let x be the height of each disk, g = gravity and p = density
Volume of each disk = πr2dx
Where r is the radius of each disk and dx is the thickness
By Pythagoras r² = 6² - x²= 36 -x²
Therefore Volume = π*(36-x²)*dx cubic metres
The distance each disk has to be lifted to escape the top of the spout = 2 + 6-x meters = (8-x)
Work needed to lift each disk to outlet = distance * mass where
mass = volume * density * gravity
= pi(36-x²)*p*g = 9800pi(36-x²)dx
dW = (8-x)* 9800pi(36-x²)dx
Since we have already accounted for the height of the spout, the work required is obtained by integrating the above expression from the bottom of the tank to the top. In other words, - 6 to + 6.
W = ⌠(8-x)*9800pi(36-x2)dx = 9800pi⌠[288 - 36x - 8x² +x³]dx
The odd terms evaluate to zero and we can rewrite the above as 2* I from 0 to 6.
W = 9800pi*2 [288x - 8x³/3] at x = 6 = 1152*19600π Joules = 22579200π joules = 70963200j
Total work required = 70.9 * 10⁶ joules
Visit here to learn more about spherical tank: https://brainly.com/question/11279278
#SPJ4
HELP PLEASE!
A local little league has a total of 80 players, of whom 20% are left-handed. How many
left-handed players are there?
Answers
Answer:
There are 16 left-handed players.
Step-by-step explanation:
Answer:
16
Step-by-step explanation:
Please help with writing linear functions

Answers
The function would be \(f(x)=\frac{1}{2}x + 1 \ and\ f(x)=\frac{1}{2}x - \frac{1}{2}\)
What is linear function?
A linear function is one with one or two variables that does not have exponents. It is a function that has a straight line graph.
A linear function has the form f(x) = mx + b, where m is the slope and b is the y-intercept. To find the equation of the linear function given the values of x and f(x), we can use two points and use the slope-intercept form of the equation.
A way to find the equation of the linear function is to use the point-slope form: f(x) = m(x-x1) + f(x1), where (x1,f(x1)) is a point on the line.
If we use the points (-4,-2) and (0,0) we can find the slope:
m = (0 - (-2)) / (0 - (-4)) = 2/4 = 1/2
then using point-slope form:
f(x) = 1/2(x - (-4)) + (-2)
f(x) = 1/2x + 1
so the equation of the linear function is f(x) = 1/2x + 1
Alternatively, we can use the two points (-2,-1) and (0,0) we can find the slope:
m = (0 - (-1)) / (0 - (-2)) = 1/2
then using point-slope form:
f(x) = 1/2(x - (-2)) + (-1)
f(x) = 1/2x - 1/2
so the equation of the linear function is f(x) = 1/2x - 1/2.
Therefore, equation f(x) = 1/2x+1 and f(x) = 1/2x - 1/2 represents the given values of x and f(x)
To know more about linear functions visit,
https://brainly.com/question/2248255
#SPJ1
Which expression is equivalent to 4^7/8
4^1/4?

Answers
Mr. Smith makes two dozen cupcakes. Each cupcake weighs 27.2 grams. What is the weight of all the cupcakes in grams?54.4 grams
A:652.8 grams
B:326.4 grams
C:163.2 grams
D:54.4 grams
Answers
Answer: The answer is 652.8
Step-by-step explanation:
First, one dozen cupcakes is 12.. So do 12*2=24 to get two dozen cupcakes.
Next, do 27.2*24=652.8