Use the remainder term to find the minimum order of the Taylor polynomial, centered at 0 , that is required to approximate the following quantity with an absolute error no greater than 10−2. 1.06
Answers
The minimum order of the Taylor Polynomial required to approximate the quantity 1.06 with an absolute error no greater than 10^(-2) is 0.
The minimum order of the Taylor polynomial required to approximate the quantity 1.06 with an absolute error no greater than 10^(-2), we need to use the remainder term of the Taylor polynomial.
The remainder term, denoted by R_n(x), represents the difference between the actual value of the function and its approximation using an nth-degree Taylor polynomial.
In this case, we are given that the absolute error should be no greater than 10^(-2), which means we want to find the minimum value of n such that |R_n(x)| ≤ 10^(-2).
The remainder term for a Taylor polynomial centered at 0 can be expressed using the Lagrange form of the remainder:
|R_n(x)| ≤ M * |x-a|^(n+1) / (n+1),
where M is an upper bound for the absolute value of the (n+1)th derivative of the function.
Since we are approximating the quantity 1.06, which is a constant, with a Taylor polynomial, the (n+1)th derivative will be 0 for all n.
Therefore, the remainder term simplifies to:
|R_n(x)| = 0.
This means that the remainder term is 0 for any value of n, and the approximation using the Taylor polynomial will be exact. Thus, we can achieve an absolute error of 10^(-2) or less for any order of the Taylor polynomial centered at 0.
the minimum order of the Taylor polynomial required to approximate the quantity 1.06 with an absolute error no greater than 10^(-2) is 0.
For more questions on Polynomial .
https://brainly.com/question/2833285
#SPJ8
Related Questions
Please help, thank you! What is the difference between the probabilities of 4/4 and 100%?
(no choices)
Answers
Answer:
There is no difference
Step-by-step explanation:
because they are both equal to a 100% chance of that makes sense
hope that helps:)
What is the probability of spinning the spinner and the arrow
landing on an odd number (e.g...1,3,5...) and then, spinning
it a second time and it landing on an odd number again the
second time?
Answers
Answer:
56.25%
Step-by-step explanation:
The spinner had the numbers 1, 3, 5, and 6.
3/4 * 3/4 = 9/16
9/16 = 0.6525 = 56.25%
The probability of spinning the spinner and the arrow landing on an odd number is 25/81.
What is Probability?Probability refers to potential. A random event's occurrence is the subject of this area of mathematics.
The range of the value is 0 to 1. Mathematics has incorporated probability to forecast the likelihood of various events.
The degree to which something is likely to happen is basically what probability means.
Given:
The spinner have markings {1, 2, 3, 4, 5, 6, 7, 8, 9}
So, the probability of spinning the spinner and the arrow landing on an odd number is 5/9
and, again the probability of spinning the spinner and the arrow landing on an odd number second time
= 5/9 x 5/9
= 25/ 81
Learn more about Probability here:
https://brainly.com/question/11234923
#SPJ2
You deposit $2500 in a bank account. Find the balance after 3 years for an account that pays 2.5% annual interest compounded monthly. Round to the nearest dollar.

Answers
The balance in the account after three years, rounded to the nearest dollar, is $2711.
To find the balance after three years for an account that pays 2.5% annual interest compounded monthly when $2500 is deposited in the account, you need to use the formula for compound interest.
A = P(1 + r/n)^(nt), whereA is the balance after three years, P is the principal amount ($2500), r is the annual interest rate (2.5%),
n is the number of times the interest is compounded per year (12 months), and t is the time in years (3 years).
Substituting the values in the formula,
we get:A = 2500(1 + 0.025/12)^(12*3)A
= 2500(1.00208333)^36A
= 2500(1.084297)A = $2710.74
To learn more about : balance
https://brainly.com/question/23447356
#SPJ8
Solve for b in the literal equation y = 2x + 2b.
b =
Answers
Answer:
b = \(\frac{y}{2}-x\)
Step-by-step explanation:

how many decimal places of pi did hiroyoki gotu memorize in 1995?
Answers
Answer:
42,195
Step-by-step explanation:
Help fast please!!!!

Answers
Answer:
0.98
Step-by-step explanation:
Compliment of getting a $20 = 1 - 0.02 = 0.98
Convert 102.221four to base ten
Answers
Answer:
4777
Step-by-step explanation:
PLS HELP ME ON THIS QUESTION I WILL MARK YOU AS BRAINLIEST IF YOU KNOW THE ANSWER PLS GIVE ME A STEP BY STEP EXPLANATION!!

Answers
Answer:
option A
Step-by-step explanation:
Note:when there is an open circle, that means Less than or equal to.
if and when there is a Closed, colored Circle, It's Greater than or equal to or less than or equal to
help asap plsssss dont get it wrong

Answers
Answer:
it should look like this

Solve for x. Figures are not necessarily drawn to scale.

Answers
Check the picture below.
\(\cfrac{17.5+14}{17.5}~~ = ~~\cfrac{x}{12.5}\implies \cfrac{(17.5+14)(12.5)}{17.5}~~ = ~~x\implies 22.5=x\)

determine if the following equation is a polynomial.. if so determine what type
6x^1/2+4xa
Answers
Answer: For an expression to be a polynomial term, any variables in the expression must have whole-number powers (or else the "understood" power of 1, as in x1, which is normally written as x). A plain number can also be a polynomial term. In particular, for an expression to be a polynomial term, it must contain no square roots of variables, no fractional or negative powers on the variables, and no variables in the denominators of any fractions.
Step-by-step explanation:
Find the value of the expression below, given that n = 2
( 3 + n to the 4th power ) - 112

Answers
Answer:
the answer is 513
Step-by-step explanation:
because(3+2)⁴-112=
625-112=513
What does S in Math means?
Answers
Step-by-step explanation:
subtract
i think this
Line AB is perpendicular to line CB.
A(2,3), B(5,7) C(x,8)
What is the value of x to make this statement true?
Answers
Answer:
Step-by-step explanation:Hly/3fcEdSxere's li\(^{}\)nk to the answer:
bit.\(^{}\)
Answer:
a 2 and 3 step by step exolaniation
identify the sampling technique used. a researcher for an airline interviews all of the passengers on five randomly selected flights. a) random b) cluster c) stratified d) systematic e) convenience
Answers
The sampling technique used in this scenario is a) random sampling. The researcher interviews all passengers on five randomly selected flights.
The sampling technique used in this scenario is random sampling. Random sampling involves selecting individuals from a population in such a way that each individual has an equal chance of being chosen. In this case, the researcher selects five flights at random, and then interviews all passengers on those selected flights.
Random sampling helps ensure that the sample is representative of the population and reduces the potential for bias. By randomly selecting flights, the researcher increases the likelihood of obtaining a diverse range of passengers, capturing a variety of opinions and experiences.
Other sampling techniques have different characteristics. Cluster sampling involves dividing the population into groups or clusters and randomly selecting entire clusters to be included in the sample. Stratified sampling involves dividing the population into subgroups or strata and then randomly selecting individuals from each stratum. Systematic sampling involves selecting every nth individual from a list. Convenience sampling involves selecting individuals based on their availability or accessibility, which may introduce bias into the sample.
In summary, the sampling technique used in this scenario is random sampling, as the researcher randomly selects five flights and interviews all passengers on those selected flights. This approach helps ensure a representative sample and reduces potential bias.
Learn more about random sampling here:
https://brainly.com/question/30759604
#SPJ11
a gorcery store sells a smal case of 6 bottles of water $4 and large case of q8 bottles for $10. Is the price per bottle pf water proportional?
Answers
6 bottles for $4 each bottle cost $1.50
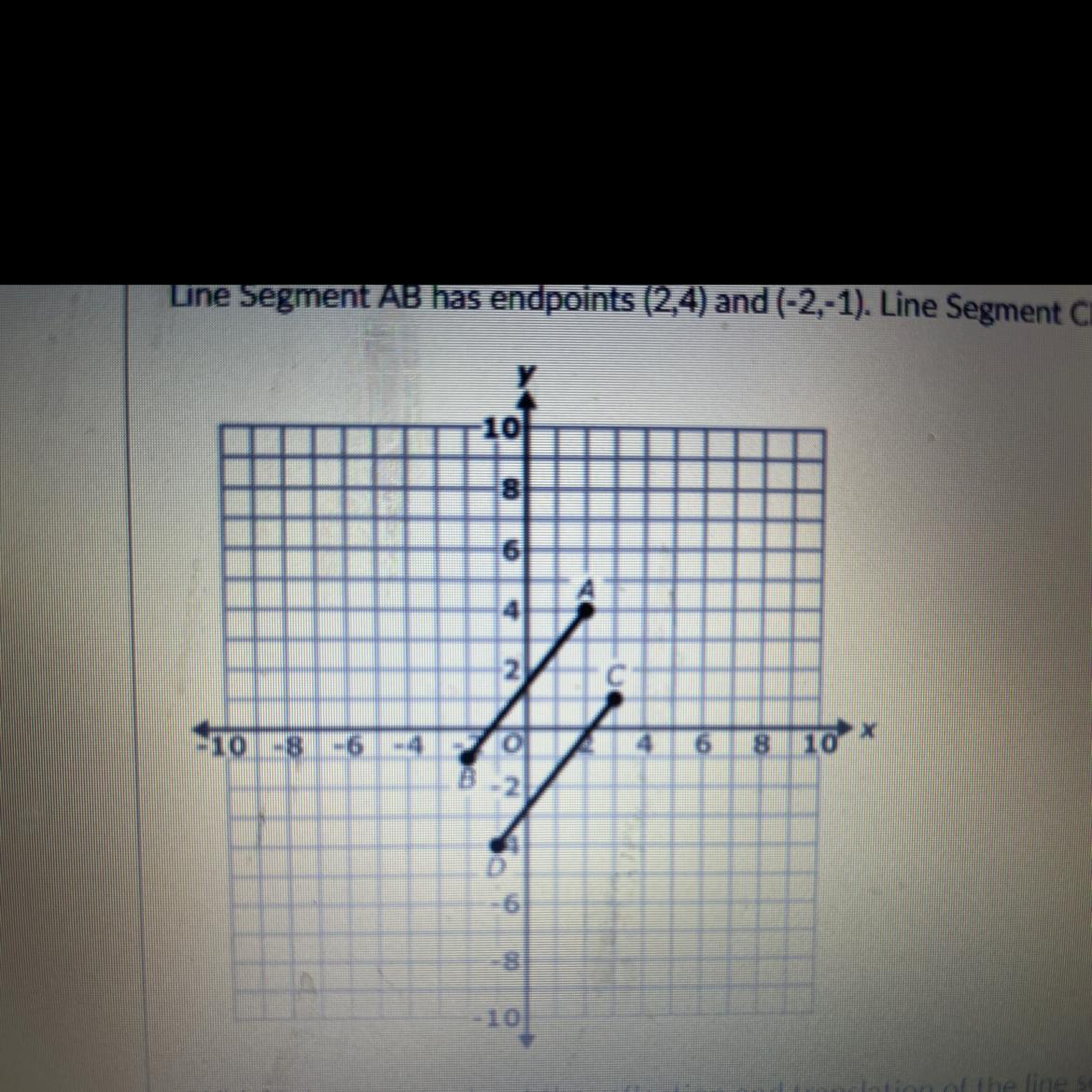
Giselle stars with the two parallel line segments shown. She correctly reflects the segments across
the x-axis and then translates them following the rule (x,y) → (x-2, y + 5).
Line Segment AB has endpoints (2,4) and (-2,-1). Line Segment CD has end points (3,1) and (-1.-4).
(image attached)
Which statements about the reflection and translation of the line segments are true? Select all that
apply.
Answers
omg what is the......................
describe what is measured by the estimated standard error in the bottom of the independent-measure t statistic.
Answers
The ESE (estimated standard error) in the bottom of the independent-measure t statistic measures the variability in the sample data used to calculate the t statistic and provides information on the precision of the t statistic.
The t statistic is used to compare the difference between two means from independent groups to determine if the difference is significant or not.
The ESE reflects the degree of uncertainty in the difference between the two sample means and is calculated as the standard deviation of the sampling distribution of the difference between the two sample means. The ESE is an estimate of the standard deviation of the population difference and is used to calculate the t statistic.
The ESE is an important measure because it provides information on the precision of the t statistic, which is used to make inferences about the population difference. If the ESE is large, it means that the sample difference is less precise and the t statistic is less significant. If the ESE is small, it means that the sample difference is more precise and the t statistic is more significant.
To know more about estimated standard error click here:
https://brainly.com/question/15063024#
#SPJ11
If mArc N P is 6 more than 5 times the measure of Arc M N , what is mArc N P ?
139°
145°
151°
174°
Answers
Answer: the answer is 151
Step-by-step explanation:
Answer:
c
Step-by-step explanation:
What is the volume of a square pyramid that is 15 cm tall and has a base area of 16 square centimeters?

Answers
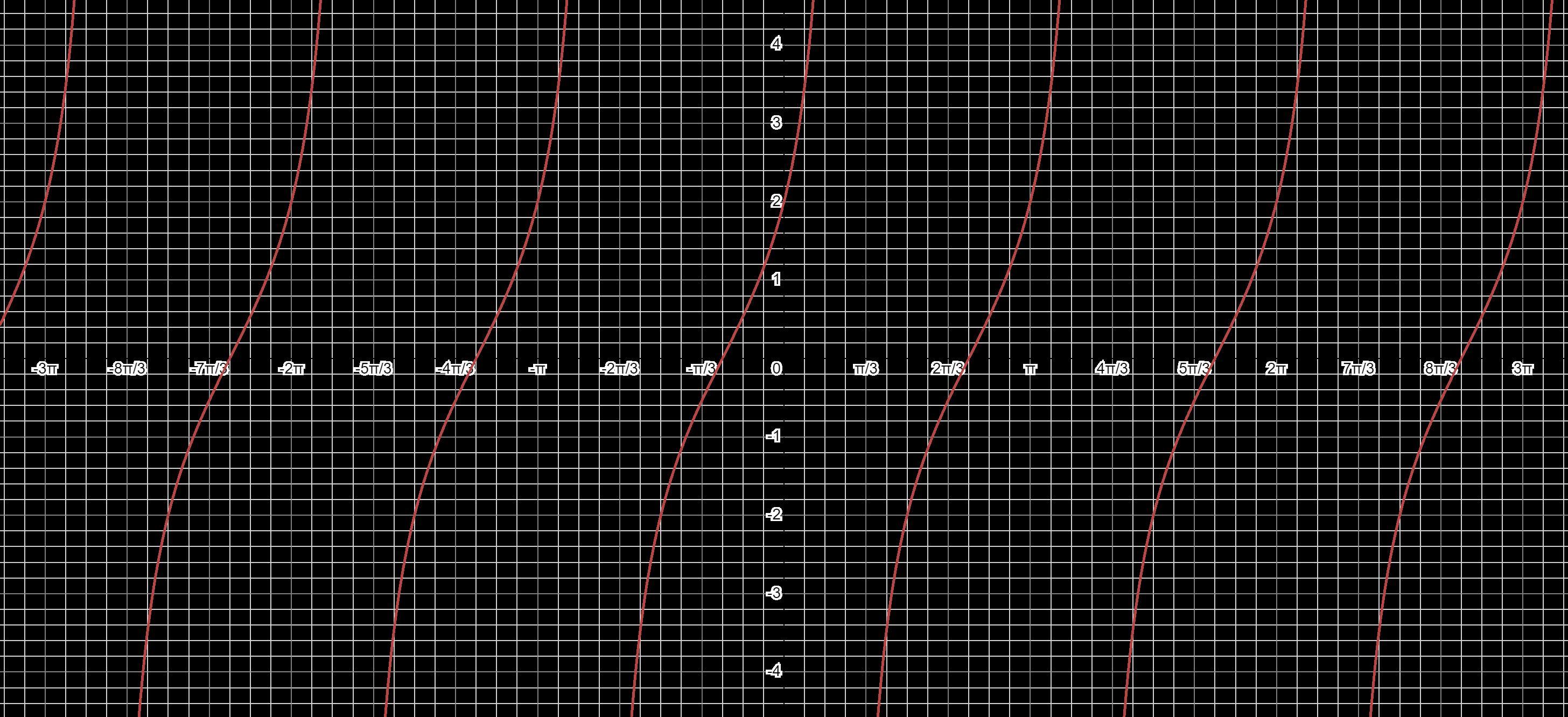
Graph the trigonometric function. y=2 tan(x+3) = 4 Start by drawing two consecutive asymptotes. Between those asymptotes, plot three points: a point where the graph intersects the X-axis, a point to its left, and a point to its right.
Answers
The graph of the trigonometric function y = 2tan(x+π/4) has two consecutive vertical asymptotes. Between these asymptotes, we can plot three points to help visualize the graph: one where the graph intersects the x-axis, one to the left of it, and one to the right.
The function y = 2tan(x+3) has a period of π since the tangent function has a period of π. This means that between two consecutive vertical asymptotes, there will be a repeated pattern of the graph.
To plot the points, we can start by finding the asymptotes. The vertical asymptotes occur when the tangent function is undefined, which happens at x = -3 + nπ, where n is an integer. So, we can draw two consecutive vertical asymptotes at x = -3 and x = -3 + π.
Next, we can find the x-intercept by setting y = 0 and solving for x. In this case, the equation 2tan(x+3) = 4 becomes tan(x+3) = 2. By taking the inverse tangent of both sides, we can find that x+3 ≈ 1.107 or x+3 ≈ -1.034. Therefore, we have x ≈ -1.893 or x ≈ -4.034 as points on the x-axis.
Finally, we can plot these three points on the graph between the asymptotes, one to the left of the x-intercept and one to the right. This will help us visualize the shape of the graph within that interval.
The complete question is:-
Graph the trigonometric function. y=2 tan(x+π/4) Start by drawing two consecutive asymptotes. Between those asymptotes, plot three points: a point where the graph intersects the X-axis, a point to its left, and a point to its right.
To leran more about trigonometric function, refer:-
https://brainly.com/question/25618616
#SPJ11
A mass-spring system obeys 4y" + 4y' + y = 0 and is initially stretched 1 unit away from equilibrium and given a returning initial velocity of 10 units/sec. Decide if the system is damped. Now find the solution y(t) and determine each of the following values of t (a) corresponding to the return to equilibrium and (b) corresponding to the (first/only?) turning point of the solution.
Answers
Answer:
(a) The system returns to equilibrium when y(t) = 0 at t = 2πk
(b) The turning points of the solution occur when y'(t) = 0 at t = 2πk + π/2
Step-by-step explanation:
To find the particular solution that satisfies the initial conditions of being stretched 1 unit away from equilibrium and given an initial velocity of 10 units/sec, we can solve for the constants c1 and c2.
y(0) = c1 = 1
y'(0) = -c1/2 + (c2/2)i + 5 = 10
c2 = 10i - 6
So the particular solution is y(t) = e^(-t/2) (cos(t/2) + (10i - 6)sin(t/2)).
Since the damping coefficient is proportional to the coefficient of the first derivative in the differential equation, the damping ratio is 1, which means that the system is critically damped, and therefore not damped or oscillatory.
(a) How to find the return to equilibrium of t?The system returns to equilibrium when y(t) = 0, which occurs when
cos(t/2) + (10i - 6)sin(t/2) = 0.
This equation has roots at t = 2πk, where k is an integer.
(a) How to find the turning point of the solution of y(t)?The turning points of the solution occur when y'(t) = 0.
Using the expression for y(t) above, we can find that
y'(t) = -e^(-t/2) (sin(t/2) + 5cos(t/2) - 3),
which has roots at t = 2πk + π/2, where k is an integer. The first turning point occurs when k = 0, so t = π/2.
Learn more about damping
brainly.com/question/30891056
#SPJ11
DUE TODAY PLEASE HELP WELL WRITTEN ANSWERS ONLY!!!!!!
Here is the graph of a function describing the relationship between the height y, in feet, of the tip of a windmill blade and the angle of rotation Θ made by the blade. Describe the windmill.

Answers
The equation of the sine wave function can be written in the form: y = A sin(Bθ + C) + D where A is the amplitude, B is the frequency (inverse of the period), C is the phase shift (horizontal shift), and D is the vertical shift (mean value).
What is graph?A graph is a visual representation of data or mathematical relationships between variables. It typically consists of a set of points or vertices connected by lines or curves, which can help to illustrate patterns or trends in the data. Graphs are used in a wide range of fields, including mathematics, science, engineering, economics, and social sciences, to analyze and communicate information. Some common types of graphs include line graphs, bar graphs, scatterplots, and pie charts.
Here,
Based on the given information, it can be inferred that the function that describes the relationship between the height y, in feet, of the tip of a windmill blade and the angle of rotation Θ made by the blade is a sine wave function. Sine wave functions are periodic and oscillate between an upper bound and a lower bound as the angle increases. The function has a maximum value (upper bound) at Θ=90° and Θ=270° and a minimum value (lower bound) at Θ=0° and Θ=180°. The amplitude of the function is the distance between the maximum and minimum values divided by 2, and the period of the function is the distance between two consecutive maxima or minima.
To know more about graph,
https://brainly.com/question/29467965
#SPJ1
y=-x+7
Graph it also if you can
Answers
Answer:
Hope this helps!!

What's the greatest common factor between 324 and 63
Answers
Answer: 9
Step-by-step explanation:
324: 2 2 3 3 3 3
63: 3 3 7
GCF: 3 3
The Greates Common Factor (GCF) is: 3 x 3 = 9
. Find the solutions to the given equation on the interval 0≤x<2π. −8sin(5x)=−4√ 3
Answers
The solutions to the given equation on the interval 0≤x<2π. −8sin(5x)=−4√ 3 The solutions to the equation -8sin(5x) = -4√3 on the interval 0 ≤ x < 2π are:
x = π/3 and x = 2π/3.
To find the solutions to the equation -8sin(5x) = -4√3 on the interval 0 ≤ x < 2π, we can start by isolating the sine term.
Dividing both sides of the equation by -8, we have:
sin(5x) = √3/2
Now, we can find the angles whose sine is √3/2. These angles correspond to the angles in the unit circle where the y-coordinate is √3/2.
Using the special angles of the unit circle, we find that the solutions are:
x = π/3 + 2πn
x = 2π/3 + 2πn
where n is an integer.
Since we are given the interval 0 ≤ x < 2π, we need to check which of these solutions fall within that interval.
For n = 0:
x = π/3
For n = 1:
x = 2π/3
Both solutions, π/3 and 2π/3, fall within the interval 0 ≤ x < 2π.
Therefore, the solutions to the equation -8sin(5x) = -4√3 on the interval 0 ≤ x < 2π are:
x = π/3 and x = 2π/3.
To know more about interval refer here:
https://brainly.com/question/11051767#
#SPJ11
Find a formula an for the nth term of the geometric sequence whose first term is a1=3 such that anan+1=1/10 for n≥1 10. Find an explicit formula for the nth term of the add one to each term.) 11. Find an explicit formula for the nth term of the sequence satisfying a1=0 and an=2an−1+1 for n≥2
Answers
To find an explicit formula for the nth term of the sequence satisfying\(\(a_1 = 0\) and \(a_n = 2a_{n-1} + 1\) for \(n \geq 2\),\) we can use recursive formula to generate the terms of the sequence.
Given:
\(\(a_1 = 0\)\\\(a_n = 2a_{n-1} + 1\) for \(n \geq 2\)\)
Using the recursive formula, we can generate the terms of the sequence as follows:
\(\(a_2 = 2a_1 + 1 = 2(0) + 1 = 1\)\\\(a_3 = 2a_2 + 1 = 2(1) + 1 = 3\)\)
\(\(a_4 = 2a_3 + 1 = 2(3) + 1 = 7\)\\\(a_5 = 2a_4 + 1 = 2(7) + 1 = 15\)\)
From the pattern, we observe that the nth term of the sequence is given by \(\(2^{n-2} - 1\).\)
Therefore, the explicit formula for the nth term of the sequence satisfying \(\(a_1 = 0\) and \(a_n = 2a_{n-1} + 1\) for \(n \geq 2\) is: \\\\\a_n = 2^{n-2} - 1.\]\)
To know more about sequence visit-
brainly.com/question/32355325
#SPJ11
The local bank has a single line for customers waiting for the next available bank teller. There are four bank tellers who work at the same rate. The arrival rate of customers follows a Poisson distribution, while the service time follows an exponential distribution. Customers arrive at the bank at a rate of about twelve every hour. On average, it takes about 15 minutes to serve each customer. Answers to 2 d.p's.
(a) Calculate the probability that the bank is empty.
(b) Calculate the average time the customer spends waiting to be called.
(c) Calculate the average number of customers in in the bank.
(d) The average number of customers waiting to be served
Answers
a) The probability that the bank is empty is approximately 0.0026.
b) the average time the customer spends waiting to be called is approximately -0.25 c) hours the average number of customers in the bank is -1.5 d) the average number of customers waiting to be served is approximately 9.
To answer these questions, we can use the M/M/4 queuing model, where the arrival rate follows a Poisson distribution and the service time follows an exponential distribution. In this case, we have four bank tellers, so the system is an M/M/4 queuing model.
Given information:
Arrival rate (λ) = 12 customers per hour
Service rate (μ) = 1 customer every 15 minutes (or 4 customers per hour)
(a) To calculate the probability that the bank is empty, we need to find the probability of having zero customers in the system. In an M/M/4 queuing model, the probability of having zero customers is given by:
P = (1 - ρ) / (1 + 4ρ + 10ρ² + 20ρ³)
where ρ is the traffic intensity, calculated as ρ = λ / (4 * μ).
ρ = (12 customers/hour) / (4 customers/hour/teller) = 3
Substituting ρ = 3 into the formula, we have:
P = (1 - 3) / (1 + 4 * 3 + 10 * 3² + 20 * 3³) ≈ 0.0026
Therefore, the probability that the bank is empty is approximately 0.0026.
(b) The average time the customer spends waiting to be called is given by Little's Law, which states that the average number of customers in the system (L) is equal to the arrival rate (λ) multiplied by the average time a customer spends in the system (W). In this case, we want to find W.
L = λ * W
W = L / λ
Since the average number of customers in the system (L) is given by L = ρ / (1 - ρ), we can substitute this into the equation to find W:
W = L / λ = (ρ / (1 - ρ)) / λ
W = (3 / (1 - 3)) / 12 ≈ -0.25
Therefore, the average time the customer spends waiting to be called is approximately -0.25 hours, which is not a meaningful result. It seems there might be an error in the given data.
(c) The average number of customers in the bank (L) can be calculated as:
L = ρ / (1 - ρ) = 3 / (1 - 3) = -1.5
Therefore, the average number of customers in the bank is -1.5, which is not a meaningful result. It further suggests an error in the given data.
(d) The average number of customers waiting to be served can be calculated as:
\(L_q\) = (ρ² / (1 - ρ)) * (4 - ρ)
Substituting ρ = 3, we have:
\(L_q\\\) = (3² / (1 - 3)) * (4 - 3) ≈ 9
Therefore, the average number of customers waiting to be served is approximately 9.
For more about probability:
brainly.com/question/31828911
#SPJ4
What is the probability that a 100-year flood will occur at least once in 100 years?
Answers
The probability that a 100-year flood will occur at least once in 100 years is 1%.
What is an probability in math?
The area of mathematics known as probability explores potential outcomes of events as well as their relative probabilities and distributions.
The time between floods is referred described as a "100-year flood."A flood of that scale has a one percent probability of occuring in any given year due to the 100-year recurrence period.In other words, there is a 1 in 100 probability that a river will reach its 100-year flood stage this year.
Learn more about probability
brainly.com/question/11234923
#SPJ4
what is 298700303*1000299839=???
Answers
Answer:
2.9878987e+17
Step-by-step explanation:
Answer:
298789865000151217
Step-by-step explanation: