using assembly language to find sum of positive odd integers
Answers
In order to find the sum of positive odd integers using assembly language, you will need to write a program that iterates through a set of numbers and adds up any positive odd integers it encounters.
The first step is to set up a loop that will iterate through a range of numbers. You can use the CMP (compare) instruction to check whether the number is positive, and the TEST instruction to check whether it is odd. If the number is both positive and odd, you can add it to a running total using the ADD instruction. You will need to keep track of the current number being evaluated and the total sum in registers. Once the loop has completed, you can output the total sum using an appropriate system call or output instruction. Overall, the process will involve setting up a loop, checking for positive odd integers, adding them to a running total, and outputting the final sum. This can be accomplished with careful programming and attention to detail.
To know more about assembly language visit:
https://brainly.com/question/14728681
#SPJ11
Related Questions
A tank is filling up with water at a rate of 3 gallons per minute. The tank already had 5 gallons in it before it started being filled. What is the starting amount of the water tank?
Answers
Answer:
5 gallons
Step-by-step explanation:
there were 5 gallons already in the tank before it started to get filled.
Find the interest rate for a $8500 deposit accumulating to $11,022, compounded annually for 7 years. The interest rate is \%. (Do not round until the final answer. Then round to two decimal places as needed.)
Answers
Answer:
3.78%
Step-by-step explanation:
The formula for compound interest is given by:
A(t) = P(1 + r/n)^(nt), where
A is the amount that has accumulated in the account,P is the principal (i.e., the deposit),r is the interest rate as a decimal (can swtich to percentage form by multiplying r by 100),n is the number of compounding periods per year (annual compound means only 1 compounding period),and t is the time in years.Thus, we can plug in 8500 for P, 11022 for A(t), 1 for n, and 7 for t to find r:
Step 1: Plug in the values and simplify:
11022 = 8500 * ( 1 + r/1)^(7 * 1)
11022 = 8500 * (1 + r)^(7)
Step 2: Divide both sides by 8500:
(11022 = 8500 * (1 + r)^(7)) / 8500
11022/8500 = (1 + r)^(7)
5511/4250 = (1 + r)^(7)
Step 3: Raise both sides to the 1/7 power (this is the same as taking the 7th root of both sides):
(5511/4250 = (1 + r)^(7))^(1/7)
1.037815641 = 1 + r
Step 4: Subtract 1 from both sides to find r:
(1.037815641 = 1 + r) - 1
0.0378154607 = r
Step 5: Multiply 0.0378154607 by 100 to find the interest rate as a percentage:
0.0378154607 * 100
3.78156407 = %
Step 6: Round to the nearest two decimal places:
3.78
Thus, the interest rate is about 3.78%
-42) what is the y intercept of the line defined by the parametric equations x(t) = -3 + 7 and y(t) = 2t - 5 ?
how do you find it
Answers
The first equation is missing the variable (t)
Please help me solve problem 2 and 3

Answers
It’s because you have to first find the area which is 100 inches
Divide it by 2 inches with is 50 inch cubes
Find the percent of decrease from 62 trees to 31 trees. Round the percent to the nearest tenth if necessary.
Answers
Answer:
50% decrease
Step-by-step explanation:
since a 31 tree decrease is half of 62 the percent would be a 50% decrease (half)
So the answer is 50% decrease
Hope this helps :)
Write an inequality for the statement:
-2/7 is at most the product of a number and -4/5.
Answers
The inequality for the statement:-2/7 is at most the product of a number and -4/5. is --4x/5 ≤ -2/7
How to write the inequality for the given statementInformation from the question
the statement: -2/7 is at most the product of a number and -4/5
Inequality is a means of representing the relationship existing between the positive and negative parts of equations, using other terms aside exactly using equal to
at most means the highest value hence the answer is either the number or less.
let the number be x
x * -4/5 ≤ -2/7
--4x/5 ≤ -2/7
Learn more about inequality:
brainly.com/question/29244324
#SPJ1
The image shown here shows a scale drawing of the average seventh grader's foot next to the world's largest foot.
If the average seventh grader's foot is approximately 10 inches long, estimate the length of the world's largest foot. Explain your thinking.

Answers
Answer:
If you are estimating....
Step-by-step explanation:
if the small foot is 10in then the bigger foot must be around 12-13inchs considering on how big it is to the little foot, so about 13 inches
Please help explanation if possible

Answers
Answer:
length = 48 feet , width = 32 feet
Step-by-step explanation:
Using
2W + 2L = 160 with W = L - 16 , then
2(L - 16) + 2L = 160 ← distribute and simplify left side
2L - 32 + 2L = 160
4L - 32 = 160 ( add 32 to both sides )
4L = 192 ( divide both sides by 4 )
L = 48
Substitute L = 48 into W = L - 16
W = 48 - 16 = 32
Thus length = 48 feet and width = 32 feet
Answer:
l = 48 cm
w = 32 cm
Step-by-step explanation:
length = l
Width w= l - 16
Perimeter = 160 ft
2*(l + w) = 160
2*(l + l -16) = 160
2*(2l - 16) = 160
Use distributive property
2*2l - 2*16 = 160
4l - 32 = 160 {add 32 to both sides}
4l = 160 + 32
4l = 192 {Divide both sides by 4}
l = 192/4
l = 48 cm
W = 48 - 16 = 32 cm
What is the range of y = cos x?
O A. x nn
OB. x+Nπ
O C. All real numbers
OD. -1 ≤ y ≤ 1

Answers
The range of the given trigonometric equation is -1≤y≤1. Therefore, option D is the correct answer.
The given trigonometric equation is y=cosx.
Find the domain by finding where the equation is defined. The range is the set of values that correspond with the domain.
Domain: (−∞,∞),{x|x∈R}
Range: [−1,1],{y|−1≤y≤1}
Therefore, option D is the correct answer.
To learn more about the trigonometric equation visit:
brainly.com/question/23599274.
#SPJ1
Give the x and y intercepts: x+3y=24
please help this is due tomorrow morning, its worth a lot of points

Answers
The y intercept is (0,8)
if the number of times you take the test were independent of the chance you fail what could that mean?
Answers
if the number of times you take the test were independent variable of the chance you fail what could that mean the difficulty of the test is consistent and unchanging.
The difficulty of the test is consistent and unchanging, making it so that the chance of failing is solely determined by the individual's performance on the test. Factors such as knowledge of the subject and the ability to focus can play a role in a person's success, but the actual chance of failing is not affected by how many times the test is taken. This means that those who fail the test will have to work harder and prepare better in order to pass it on the next attempt. Taking the test multiple times does not guarantee a higher chance of success, as the difficulty remains the same each time due to independent variable.
Learn more about independent variable here
https://brainly.com/question/29430246
#SPJ4
PLEASE HELP
What is the product of (-a + 3)(a + 4)?
A. - a2 - a - 12
B. a2 - a + 12
C. - a2 - a + 12
D. a2 - a - 12
Answers
Answer:
-a^2-a+12
Step-by-step explanation:
Answer:
Option C.
\(-a^{2}-a+12\)
Step-by-step explanation:
1. Distributive multiply
\(-a*(a+4)+3*(a+4)\)
2. Distributive multiply
\(-a*a-a*4+3*(a+4)\)
3. Multiply terms to exponential form
\((-1) *a^{2}-a*4+3*(a+4)\)
4. Multiply constants
\(-a^{2}-4*a+3*(a+4)\)
5. Distributive multiply
\(-a^{2}-4a+(3*a+3*4)\)
6. Multiply constants
\(-a^{2}-4a+(3a+12)\)
7. Reorder terms
\(-a^{2} -4a+(12+3a)\)
8. Add terms
\(-a^{2}-a+12\)
Elena wants to build a one-sample z interval to estimate what proportion of computers produced at a
factory have a certain defect. She chooses a confidence level of 94%. A random sample of 200 computers
shows that 12 computers have the defect
What critical value z' should Elena use to construct this confidence interval?
Answers
Answer:
Z = 1.88
Step-by-step explanation:
In a sample with a number n of people surveyed with a probability of a success of \(\pi\), and a confidence level of \(1-\alpha\), we have the following confidence interval of proportions.
\(\pi \pm z\sqrt{\frac{\pi(1-\pi)}{n}}\)
In which
z is the zscore that has a pvalue of \(1 - \frac{\alpha}{2}\).
94% confidence level
So \(\alpha = 0.06\), z is the value of Z that has a pvalue of \(1 - \frac{0.06}{2} = 0.97\), so \(Z = 1.88\).
The critical z-value elena should use to construct the given confidence interval is; 1.88
We are given;
Confidence level = 94%Sample proportion; p^ = 12/200 = 0.06Sample size; n = 200Formula for confidence intervals of proportion is;
CI = p^ ± z√(p^(1 - p^)/n)
Since we are given Confidence level of 94%, the significance level is;
α = 100% - 94%
α = 0.06
The the z-score will be at the p-value of 1 - α/2
P-value = 1 - (0.06/2) = 0.97
From online p-value from z-score calculator, we have; z-score = 1.88
Read more about confidence intervals at; https://brainly.com/question/16236451
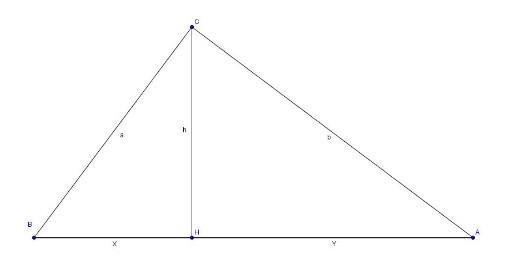
Let $\triangle ABC$ be a right triangle, and let $H$ be the point on side $\overline{AB}$ so that $\overline{CH} \perp \overline{AB}. $
[asy]
// Coordinates for 3-4-5 triangle
pair A = (5, 0);
pair B = (0, 0);
pair C = (1. 8, 2. 4);
pair H = foot(C, A, B);
draw(A--B--C--cycle);
draw(rightanglemark(B, C, A));
draw(C--H);
draw(rightanglemark(C,H,A));
label("$A$", A, E);
label("$B$", B, W);
label("$C$", C, N);
label("$H$", H, S);
label("$x$", midpoint(B--H), S);
label("$y$", midpoint(A--H), S);
label("$h$", midpoint(C--H), E);
label("$a$", midpoint(B--C), NW);
label("$b$", midpoint(A--C), NE);
[/asy]
Prove that
\[(x + h)^2 + (y + h)^2 = (a + b)^2. \]
Answers
For ABC is a right angled triangle and let H be a point on side AB so that CH is prependicular to AB. Then ( x + h)² + ( y + h)² = (a + b)².
We have a right angled triangle ABC with angle B = 90° and length of side AB=x + y
Length of side BC = a
Length of side AC = b
Now, in ∆BHC and ∆BCA
BC = BC ( common side) measure of angle ACB = measure of angle BHC = 90° Also, angle ABC = angle HBC ( common angle)by SAS( side angle side) Congruence rule, ∆BHC is similar to ∆ BCA. So,
HC / BC = CA / BA
=> h/a = b/( x + y) ---(1)
From right angled triangle BCH and ACH,
x² + h² = a² --(2) and y² + h² = b² --(3)
from equation (1),
h( x + y) = ab
=> hx + hy = ab
2xh + 2yh = 2ab -- (4) (multiply through by 2)
Adding expansion from equation (2),(3) and (4), (x² + h² ) + (y² + h²) + ( 2xh + 2yh) = a² + b² + 2ab
=> (x² + 2xh + h²) + (y² + 2yh + h²) = (a + b)²
=> ( x + h)² + ( y + h)² = (a + b)² ( since, whole square formula)
Hence, proved.
To learn more about right angled triangle, visit:
https://brainly.com/question/64787
#SPJ4
A "blink of an eye" is a time interval of about 150 ms for an average adult. The "closure" portion of the blink takes only about 55 ms. Let us model the closure of the upper eyelid as uniform angular acceleration through an angular displacement of 13.4
∘
What is the value of the angular acceleration the eyelid undergoes while closing? rad/s
2
Answers
The angular acceleration the eyelid undergoes while closing is approximately 13.93 rad/s².
To find the angular acceleration (α) of the eyelid while closing, we can use the equations of rotational motion. The given data is:
Angular displacement (θ) = 13.4 degrees
Time interval for closure (Δt) = 55 ms = 0.055 s
We can use the following equation to relate angular displacement, angular acceleration, and time:
θ = 0.5 * α * t²
Plugging in the values:
13.4 degrees = 0.5 * α * (0.055 s)²
Let's convert the angular displacement from degrees to radians:
θ = 13.4 degrees * (π/180) radians/degree
θ ≈ 0.2332 radians
Now, we can rearrange the equation to solve for α:
α = (2θ) / (t²)
α = (2 * 0.2332 radians) / (0.055 s)²
Calculating the value:
α ≈ 13.93 radians/s²
Therefore, the angular acceleration the eyelid undergoes while closing is approximately 13.93 rad/s².
To learn more about angular acceleration
https://brainly.com/question/13014974
#SPJ11
A boat traveled downstream a distance of 54 mi and then came back right back. If the speed of the current was 12 mph and the total trip took 6 hours, find the average speed of the boat relative to the water.
Answers
Answer:
18 mph.-
Step-by-step explanation:
This is 2*54 / 6
= 18 m p h.
Write an equation in slope-intercept form that passes through (5, -8) and runs perpendicular to y = 5/2x + 4
Answers
y= (-2/5)x-6
Step-by-step explanation:
the slope of the line perpendicular the the given line is found by the formula m1.m2= -1 hence m2= -2/5
using the slope-intercept form
y+8= -2/5(x-5) y= (-2/5)x-6
Plz help fast will mark brainliest!!!

Answers
There are many cones with a height of 12 inches. Let r represent the radius and v represent the volume of these cones
Answers
The relationship between the radius (r) and the volume (v) of these cones is v = 4πr^2.
We have multiple cones with a height of 12 inches, and we are representing the radius of the cones as r and the volume as v. We need to determine the relationship between the radius and the volume of these cones.
To find the relationship between the radius and the volume of the cones, we can follow these steps:
The formula for the volume of a cone is given by V = (1/3) * π * r^2 * h, where V is the volume, π is a constant (approximately 3.14), r is the radius, and h is the height.
Since we have multiple cones with the same height of 12 inches, we can substitute h = 12 into the volume formula: V = (1/3) * π * r^2 * 12.
Simplify the equation: V = 4πr^2.
Therefore, the relationship between the radius (r) and the volume (v) of these cones is v = 4πr^2.
To learn more about formula for the volume of a cone click here:
brainly.com/question/29767724
#SPJ11
The equation of the conic with focus at (1,−1) directrix along x−y+1=0 and with eccentricity 2 is.O x2−y2=1O xy=1O 2xy−4x+4y+1=0O 2xy+4x−4y−1=0
Answers
The equation of the conic with Points at (1,−1) directrix along x−y+1=0 and with eccentricity 2 is 2xy - 4x -4y +1 = 0 .
Equation:
An equation is a formula that connects two expressions with the equal sign = to indicate that they are equal. Solving an equation involving variables involves determining which values of the variables make the equation true. The variables for which the equation must be solved are also called unknowns, and the values of the unknowns that satisfy the equation are called solutions of the equation. There are two types of comparisons: identity comparisons and conditional comparisons. The identity is true for all values of the variable. Conditional comparisons are only true for certain values of variables
According to the Question:
Let P(x, y) be any point on conic. Then,
\(\sqrt{(x-1)^2+(y+1)^2}\) = \(\sqrt{2} (\frac{x-y+1}{\sqrt{2} } )\)
⇒ (x-1)²+(y+1)² = (x- y+ 1)²
⇒ 2xy - 4x -4y +1 = 0
The above equation is the required equation of conic.
Complete Question:
The equation of the conic with focus at (1,−1) directrix along x−y+1=0 and with eccentricity 2 is.
1) x²− y²=1O
2) xy =1O
3) 2xy−4x+4y+1 =0
4) 2xy+4x−4y−1 =0
Learn more about Equation:
https://brainly.com/question/29657983
#SPJ4
–12 + (–7) + 11 how do i get it right it is hard
math
Answers
Answer:
-8
Step-by-step explanation:
-12 + (-7) + 11 combine like terms
-19 + 11 add + 11 to -19
-8
RATING BRAINLIEST Which of the following demonstrates the Distributive Property?
4(2a + 3) = 8a + 3
4(2a + 3) = 2a + 12
4(2a + 3) = 6a + 7
4(2a + 3) = 8a + 12
Answers
Answer:
D: 4(2a+3)=8a+3
Step-by-step explanation:
4x2a = 8a and 4x3 = 12
Answer:
just saying this so other can get brainliest
Step-by-step explanation:
d
100 POINTS
PLEASE DO THESE FOUR QUESTIONS (even if it’s just one)
1. write a number sentence expressing the value of the missing angle in the diagram below
2. write a number sentence expressing the value of r in the diagram
3. label the diagram below so that one pair of parallel lines, and one pair of equal lines
4. use the index laws to simplify the expression below, giving your answer with positive indices. SHOW ALL WORKING OUT.
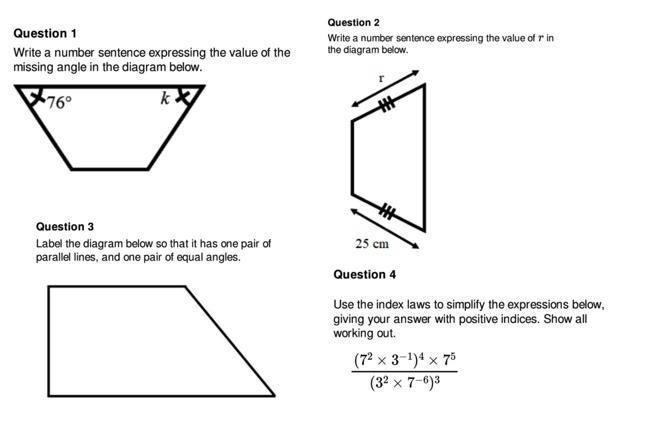
Answers
Step-by-step explanation:
1. k = 76°
2. r = 25cm
3. as the drawing attached
one pair of parallel lines : AB and DC
one pair of equal angles : L A and L D
4. (7²× 3`¹)⁴×7^5 / (3² × 7^(-6))³
= (7^8 × 3`⁴)×7^5/ (3² × 7^(-6))³
= (7^13 × 3`⁴)/ (3^6 × 7^(-18))
= (7^(31) × 3^(-10))
= 7^31 / 3^10

what is the numerical answer for 49 1/2?
Answers
Answer:
49.50
Step-by-step explanation:
All you do is turn the fraction into a decimal so:
1/2 = .50
so the answer would be 49.50
Ace Carlos
A polynomial identity is shown, where p stands for a polynomial.
x3+y3=p(x2−xy+y2)
ON TIMED ASSESMENT PLEASE HELP ASAP
Answers
Answer:
p=x+y
Step-by-step explanation:
Answer:
p=x+y
Step-by-step explanation:
that is the answer
How many 4th cups of flour are in 3 3/4 cups
Answers
Answer: 12 cups
Step-by-step explanation:
Tyler thinks he knows one of the linear factors of . After finding that , he suspects that is a factor of P(x). Here is the diagram he made to check if he’s right, but he set it up incorrectly. What went wrong?
Answers
Linear factors are the factors of a polynomial
What went wrong is that: Tyler's linear factors are incorrect
The polynomial function is given as:
Rewrite as:
Further rewrite as:
Factorize the above polynomial
Factor out x - 1 from the polynomial
This means that:
The linear factors are x - 1 and x^2 - 8x + 15
From the given diagram, Tyler's linear factors are x - 1 and x^2 - 8x - 15
Hence, Tyler's linear factors are incorrect
sol
2.18 Show that the equation \[ 4 x^{2} u^{n}+\left(1-x^{2}\right) u=0 \]
has two solutions of the form \[ \begin{array}{l} u_{1}=x^{\frac{1}{2}}\left[1+\frac{x^{2}}{16}+\frac{x^{4}}{1024}+\cdots\righ
Answers
The equation \(4x^2u^n + (1-x^2)u = 0\) has two solutions. One solution is given by \(u_1 = x^{1/2}\left(1 + \frac{x^2}{16} + \frac{x^4}{1024} + \dots\right)\). The other solution is not provided in the given question.
To find the solutions, we can rewrite the equation as \(u^n = -\frac{1-x^2}{4x^2}u\). Taking the square root of both sides gives us \(u = \pm\left(-\frac{1-x^2}{4x^2}\right)^{1/n}\). Now, let's focus on finding the positive solution.
Expanding the expression inside the square root using the binomial series, we have:
\[\left(-\frac{1-x^2}{4x^2}\right)^{1/n} = -\frac{1}{4^{1/n}x^{2/n}}\left(1 + \frac{(1-x^2)}{4x^2}\right)^{1/n}\]
Since \(|x| < 1\) (as \(x\) is a fraction), we can use the binomial series expansion for \((1+y)^{1/n}\), where \(|y| < 1\):
\[(1+y)^{1/n} = 1 + \frac{1}{n}y + \frac{1-n}{2n^2}y^2 + \dots\]
Substituting \(y = \frac{1-x^2}{4x^2}\), we get:
\[\left(-\frac{1-x^2}{4x^2}\right)^{1/n} = -\frac{1}{4^{1/n}x^{2/n}}\left(1 + \frac{1}{n}\cdot\frac{1-x^2}{4x^2} + \frac{1-n}{2n^2}\cdot\left(\frac{1-x^2}{4x^2}\right)^2 + \dots\right)\]
Simplifying and rearranging terms, we find the positive solution as:
\[u_1 = x^{1/2}\left(1 + \frac{x^2}{16} + \frac{x^4}{1024} + \dots\right)\]
The second solution is not provided in the given question, but it can be obtained by considering the negative sign in front of the square root.
Learn more about equation here: brainly.com/question/29657983
#SPJ11
use the relationship between the electric field and the electric potential to find the electric field along the x axis
Answers
Follow these steps below to find electric field along the x axis.
1. Understand the relationship
2. Determine the electric potential function
3. Take the derivative of the electric potential function
4. Find the electric field at the desired location
lets briefly discuss these steps:
1. Understand the relationship: The electric field (E) and electric potential (V) are related by the equation E = -dV/dx, where dV is the change in potential, dx is the change in position along the x-axis, and the negative sign indicates that the electric field points from higher potential to lower potential.
2. Determine the electric potential function: You'll need the electric potential function V(x) for the problem you're working on. This function will be given or can be derived from other information in the problem.
3. Take the derivative of the electric potential function: Differentiate the electric potential function V(x) with respect to the position x to find the electric field as a function of position E(x).
4. Find the electric field at the desired location: Evaluate E(x) at the specific point along the x-axis where you want to find the electric field.
By following these steps, you can find the electric field along the x-axis using the relationship between the electric field and the electric potential.
Learn more about electric potential.
brainly.com/question/17058027
#SPJ11
i dont know how to sovle this problem y minus 12
Answers
Have they given you a y=something? If not y-12 is the answer. If they have given a number for y, put that in the y's place. An example would be:
y=20. What is y-12 and you would put 8.