Using the Pythagorean theorem decided if the values 10 11 2 could be a right triangle
Answers
We have to check if a triangle with sides of length 10, 11 and 2 could be a right triangle.
If it is a right triangle, it should verify the Pythagorean theorem:
\(c^2=a^2+b^2\)where c is the hypotenuse, that we can identify as the longest side.
In this case the hypotenuse would be 11, as it is the longest side.
Then, 2 and 10 would be the legs.
We can then check the Pythagorean theorem:
\(\begin{gathered} c^2=a^2+b^2 \\ 11^2=10^2+2^2 \\ 121=100+4 \\ 121\ne104\to Not\text{ }verified \end{gathered}\)As the sides do not check the Pythagorean theorem, the sides do not correspond to a right triangle.
Answer: The sides do not correspond to a right triangle.
Related Questions
Assume that when human resource managers are randomly selected, 41% say job applicants should follow up within two weeks. If 8 human resource managers are randomly selected, find the probability that at least 4 of them say job applicants should follow up within two weeks.
Answers
Using the binomial distribution, it is found that there is a 0.4295 = 42.95% probability that at least 4 of them say job applicants should follow up within two weeks.
For each manager, there are only two possible outcomes. Either they say job applicants should follow up within two weeks, or they do not say it. The opinion of a manager is independent of any other manager, which means that the binomial distribution is used to solve this question.
Binomial probability distribution
\(P(X = x) = C_{n,x}.p^{x}.(1-p)^{n-x}\)
\(C_{n,x} = \frac{n!}{x!(n-x)!}\)
The parameters are:
n is the number of trials.x is the number of successes.p is the probability of a success on a single trial.In this problem:
41% say job applicants should follow up within two weeks, thus \(p = 0.41\)8 managers are selected, thus \(n = 8\).The probability that at least 4 of them say job applicants should follow up within two weeks is \(P(X \geq 4)\), which is given by:
\(P(X \geq 4) = 1 - P(X < 4)\)
In which:
\(P(X < 4) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3)\)
Then:
\(P(X = x) = C_{n,x}.p^{x}.(1-p)^{n-x}\)
\(P(X = 0) = C_{8,0}.(0.41)^{0}.(0.59)^{8} = 0.0147\)
\(P(X = 1) = C_{8,1}.(0.41)^{1}.(0.59)^{7} = 0.0816\)
\(P(X = 2) = C_{8,2}.(0.41)^{2}.(0.59)^{6} = 0.1985\)
\(P(X = 3) = C_{8,3}.(0.41)^{3}.(0.59)^{5} = 0.2759\)
\(P(X < 4) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) = 0.0147 + 0.0816 + 0.1985 + 0.2759 = 0.5707\)
\(P(X \geq 4) = 1 - P(X < 4) = 1 - 0.5705 = 0.4295\)
0.4295 = 42.95% probability that at least 4 of them say job applicants should follow up within two weeks.
A similar problem is given at https://brainly.com/question/25166697
Hi Guys
Please answer this question. I will choose Brainliest.
Also please do a step by step method.
Worth 10 points and it is a Maths question.
Cheers,
Jake

Answers
Answer:
In simplifying this is simple.
2-4 x + 3x-12.2x+9x2-x-12pls help will give brainliest
Given f(x)=2/x^2+3x-10, which of the following is true?
A. f(x) is positive for all x<-5
B. f(x) is negative for all x<-5
C. f(x) is positive for all x<2
D. f(x) is positive for all x>2
Answers
The only true statement about the domain of the given function is:
B. f(x) is negative for all x < -5
How to solve for the domain of the function?The domain of a function is defined as the set of values that we can possibly plug into our function. This set is the x values in a function such as f(x).
Now, we are given the function as:
f(x) = \(\frac{2}{x^{2} } + 3x - 10\)
When x < -5, we have:
f(-4) = \(\frac{2}{(-4)^{2} } + 3(-4) - 10\)
f(-4) = -21.875
This suggests that for all values below x = -5 will result in negative values
When x > 2
f(3) = \(\frac{2}{3^{2} } + 3(3) - 10\)
f(3) = -0.78
Thus, it will get positive for higher values but it can also be negative as seen here.
Read more about Domain of Function at: https://brainly.com/question/10197594
#SPJ1
2. the sum of x and 9
Answers
Answer:
x + 9
Step-by-step explanation:
The sum of x and 9,
x + 9
Determine whether the following system of linear equations have no solution, infinitely many solution or unique solutions.x+2y=3,2x+4y=15A.No solutionB.Infinitely many solutionC.Unique solutionD.Cannot be determined
Answers
C. Unique solution. The system of linear equations have a unique solution because the equations are consistent and have the same number of variables and equations.
The given system of linear equations is x+2y=3 and 2x+4y=15. To determine whether the system of linear equations have no solution, infinitely many solution or unique solutions, we need to solve the system of equations. Firstly, we expand and simplify both equations to get x+2y=3 and 2x+4y=15. Then, we compare the coefficients of the equations to determine if the system of equations is consistent, inconsistent or dependent. Since the equations are consistent and have the same number of variables and equations, we can solve the system of equations. By isolating the variables and using the substitution method, we can solve the system of equations to get x=3 and y=3. This means that the system of linear equations have a unique solution.
Learn more about equation here
https://brainly.com/question/29657983
#SPJ4
5. El bloque de la figura se encuentra en reposo en el momento en que empiezan a actuar las fuerzas.
F₁ = 25 N
F, = 22.6 N
m = 2 kg
a. Encontrar el valor de la fuerza resultante.
b. Determina su aceleración.
C. Calcula la velocidad del bloque a los 5 segundos de movimiento.
Answers
The resultant force acting on the block is 47.6N.
The acceleration of the block will be 23.8 m/s².
The speed of the block after 5 seconds of movement is 119 m/s.
What is the resultant force?In this question, we need to make use of Newton's second law, hence:
resultant force = mass × acceleration
So, for question a. The value of the resultant force will be obtained by adding the two forces together:
resultant force = F₁ + F₂
= 25N + 22.6N
= 47.6N
b. Its acceleration will be:
acceleration = resultant force / mass
= 47.6N / 2kg
= 23.8 m/s²
c. The speed of the block after 5 seconds of movement will be:
Velocity (v) = u + at
velocity = initial velocity + acceleration x time
Based on the block was initially at rest, the initial velocity is 0.
Hence:
V = acceleration x time
= 23.8 m/s² x 5s
= 119 m/s
Hence the speed of the block after 5 seconds of movement will be: 119 m/s.
Learn more about resultant force from
https://brainly.com/question/25239010
#SPJ1
See full text below
The block in the figure is at rest when the forces begin to act.
F₁ = 25N
F, = 22.6 N
m = 2kg
to. Find the value of the resultant force.
b. Determine its acceleration.
C. Calculate the speed of the block after 5 seconds of movement.
{(x, y): y = 2 |x + 1| and x {-2, -1, 0, 1, 2}}. (-2, __)
Answers
Answer: 37-07
Step-by-step explanation:
The statement "tane = -1/2/2, e is in quadrant 3": CSC8 = 13, and the terminal point determined by theta is in quadrant 3
Answers
The correct answers are Options: B and C as both are applicable in this case.
How to determine the correct option?The terminal point determined by theta can not be in quadrant 3 since tan theta is greater than zero in this quadrant.
In addition, if tan theta =-12/5 then csc theta = ±13/12 since the terminal point determined by theta can be in quadrant 2 where sine theta and consequently csc theta would be positive or in quadrant 4 where csc theta would be negative.
In conclusion, we chose Options: B and C as correct answers as both are applicable in this case.
Learn more about Trigonometry on https://brainly.com/question/29002217
S#PJ1
Corrected Question
The statement "tan theta=-12/5 , csc theta = -13/5 , and the terminal point determined by theta is in quadrant 3":
A. cannot be true because tan theta must be less than 1.
B. cannot be true because tan theta is greater than zero in quadrant 3.
C. cannot be true because if tan theta = -12/5 , then csc theta = +/- 13/12
D. cannot be true because 12^2 + 5^2 ≠ 1
Susan threw a softball 42 yards on her first try and 51 1/2 yards on her second try.
How much farther did she throw the softball on her second try than her first?
Express your answer in feet and inches.
9 ft 12 in.
28 ft 12 in.
28 ft 6 in.
126 ft
Answers
Answer:
the answer is 9 ft 12in here is a simple formula to find how many inches are In a yard
1 yard = 24 inches and half of 24 equals 12
I have 18 tens and 22 ones what am
I
Answers
Answer:
A number. :) lol
Step-by-step explanation:
I don’t know if it is right though....
A boy drops his toy car from the top floor of his house. The time it takes for the toy to fall from a height of 13 feet is given by the equation
h=94−16t^2, where t is the time in seconds. Determine the time it takes the toy to fall to the bottom floor.

Answers
It takes the toy car 2.43 seconds to fall to the bottom floor, answer choice is B. 9/4 seconds, which is equal to 2.25 seconds.
Describe Equation?An equation is a mathematical statement that asserts that two expressions are equal. An equation consists of two sides, the left-hand side and the right-hand side, separated by an equal sign (=).
For example, 2x + 5 = 11 is an equation, where the left-hand side is 2x + 5 and the right-hand side is 11. This equation asserts that the expression 2x + 5 is equal to 11, and the value of x can be determined by solving for x.
Equations can be simple or complex, and they can involve one or more variables. They can also be linear or nonlinear, depending on the nature of the expressions involved.
Solving an equation involves finding the values of the variables that make the equation true. This may involve applying algebraic operations and simplification techniques to isolate the variable on one side of the equation.
Equations are used in many areas of mathematics, science, engineering, and economics, and they provide a powerful tool for modeling and analyzing real-world situations. They are also used extensively in computer programming and cryptography, where they play a critical role in the development of algorithms and data encryption methods.
We have the equation \(h = 94 - 16t^2\), where h is the height of the toy car in feet and t is the time in seconds.
When the toy car reaches the bottom floor, its height will be h = 0. So we can set the equation equal to 0 and solve for t:
\(0 = 94 - 16t^216t^2 = 94t^2 = 94/16\)
\(t = \sqrt{(94/16)} = \sqrt{(23.5/4)} = 2.43 seconds\) (rounded to two decimal places)
Therefore, it takes the toy car 2.43 seconds to fall to the bottom floor.
The closest answer choice is B. 9/4 seconds, which is equal to 2.25 seconds.
To know more about decimal visit:
brainly.com/question/29018620
#SPJ1
Kevin's supervisor, Jill, has asked for an update on today's sales, Jill is pretty busy moving back and forth between different store locations. How can Kevin most effectively deliver an update to her ? a) Call with a quick update Ob ) Send a detailed text message c ) Book a one-hour meeting for tomorrow morning d) Send a detailed email
Answers
In ΔHIJ, h = 33 cm, i = 61 cm and j=39 cm. Find the area of ΔHIJ to the nearest square centimeter.
Answers
Thus, the area of ΔHIJ using the Heron's formula is found as 580.47 square centimeter.
Explain about the Heron's formula:Heron of Alexandria (c. 62 ce) is credited with developing the Heron's formula, which determines the area of a triangle in regards of the lengths of its sides. If the side lengths are represented by the symbols a, b, and c: √s(s - a)(s - b)(s - c)
where s = half the perimeter,
s = (a + b + c)/2.
given data:
In ΔHIJ,
h = 33 cm, i = 61 cm and j =39 cm.semi -perimeter s = (i + j + h) / 2
s = (33 + 61 + 39) / 2
s = 66.5
Now,
s - h = 66.5 - 33 = 33.5
s - i = 66.5 - 61 = 5.5
s - j = 66.5 - 39 = 27.5
area of ΔHIJ = √s(s - h)(s - i)(s - j)
area of ΔHIJ = √66.5*33.5*5.5*27.5
area of ΔHIJ = √336947.1875
area of ΔHIJ = 580.47
Thus, the area of ΔHIJ using the Heron's formula is found as 580.47 square centimeter.
Know more about the Heroin's formula:
https://brainly.com/question/17617609
#SPJ1

A rectangle is 15 feet long and 9 feet wide. Find its area,A24 square feetB 126 square feetC 135 square feetD 45 square feet
Answers
We can draw the following picture:
the area A is given by
\(\begin{gathered} A=b\cdot h \\ A=15\cdot9 \\ A=135 \end{gathered}\)therefore, the area is 135 ft^2. Which corresponds to option C.

An arrow is shot from 3 ft above the top of a hill with a vertical upward velocity of 108 ft/s. If it strikes the plain below after 9.5 s, how high is the hill?
If the arrow is launched at t0, then write an equation describing velocity as a function of time?
Answers
The height of the hill is approximately 25.73 ft. Where v0 is the initial velocity (108 ft/s), g is the acceleration due to gravity \((-32.2 ft/s^2)\),
To find the height of the hill, we can use the formula for the vertical position of an object under constant acceleration:
h = h0 + v0t + 1/2at^2
where h is the final height, h0 is the initial height, v0 is the initial velocity, t is the time, and a is the acceleration due to gravity (-32.2 ft/s^2).
In this case, we are given that the initial height h0 is 3 ft, the initial velocity v0 is 108 ft/s, and the time t is 9.5 s. We want to find the height of the hill, which we can denote as h_hill. The final height is the height of the plain, which we can denote as h_plain and assume is zero.
At the highest point of its trajectory, the arrow will have zero vertical velocity, since it will have stopped rising and just started to fall. So we can set the velocity to zero and solve for the time it takes for that to occur. Using the formula for velocity under constant acceleration:
v = v0 + at
we can solve for t when v = 0, h0 = 3 ft, v0 = 108 ft/s, and a = -32.2 ft/s^2:
0 = 108 - 32.2t
t = 108/32.2 ≈ 3.35 s
Thus, it takes the arrow approximately 3.35 s to reach the top of its trajectory.
Using the formula for the height of an object at a given time, we can find the height of the hill by subtracting the height of the arrow at the top of its trajectory from the initial height:
h_hill = h0 + v0t + 1/2at^2 - h_top
where h_top is the height of the arrow at the top of its trajectory. We can find h_top using the formula for the height of an object at the maximum height of its trajectory:
h_top = h0 + v0^2/2a
Plugging in the given values, we get:
h_top = 3 + (108^2)/(2*(-32.2)) ≈ 196.78 ft
Plugging this into the first equation, we get:
h_hill = 3 + 108(3.35) + 1/2(-32.2)(3.35)^2 - 196.78
h_hill ≈ 25.73 ft
If the arrow is launched at t0, the equation describing velocity as a function of time would be:
v(t) = v0 - gt
For such more questions on velocity
https://brainly.com/question/25749514
#SPJ8
4 cm
5 cm
What is the volume of the prism?
20 cm
36 cm3
47 cm
60 cm3
3 cm
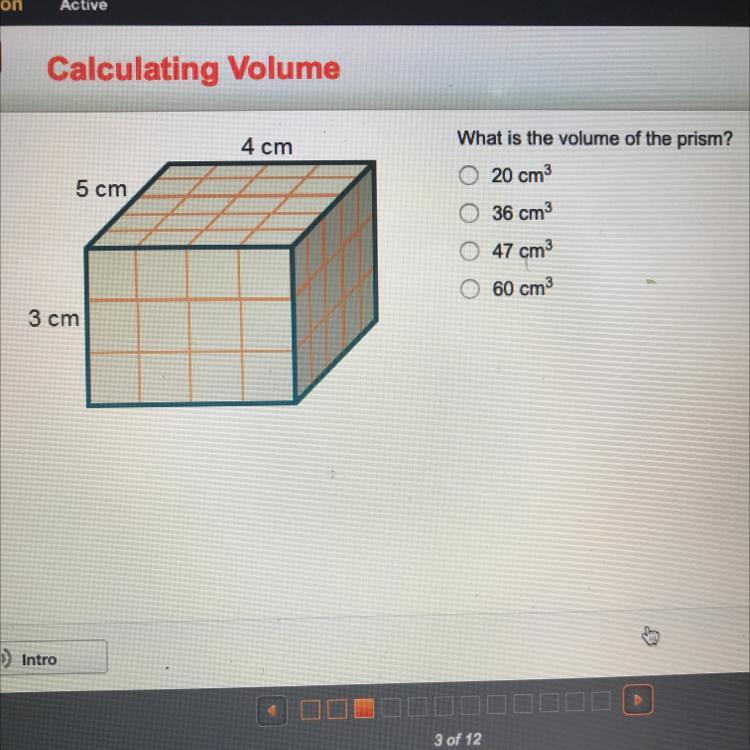
Answers
To find the volume it’s v=lwh
3 Jack walk from Santa Clara to Polo Allo. Il took I hour 25 min to walk from Santa Clot to Los Altos. Than it took 25 minute of wal from los altos to Palo buto. He arrived in Palo alto at 2:45 P.M. of what time die Santa Clara ? he leave Santa clara
Answers
The time Jack left Santa Clara is 1 : 55 pm
What is word problem?A word problem in math is a math question written as one sentence or more. These statements are interpreted into mathematical equation or expression.
The time for Jack to walk to lose Altos is 25 min and he uses another 25mins to work to Palo alto.
Therefore, the total time he spent is
25mins + 25 mins = 50 mins
He arrived Palo at 2 :45 pm, therefore the time he left Santa Clare will be ;
2:45 pm = 14 :45
= 14:45 - 50mins
= 13:55
= 1 : 55pm
Therefore he left at 1:55 pm
learn more about word problem from
https://brainly.com/question/21405634
#SPJ1
Mika can eat 21 hot dogs in 6 minutes. She wants to know how many minutes (m) left parenthesis, m, right parenthesis it would take her to eat 35 hot dogs if she can keep up the same pace.
Answers
Answer:
10 mins
Step-by-step explanation:
Proportion:
21/6=35/x
x=(35*6)/21
x=10
Hope this helps plz hit the crown :D
Answer:
10 mintes
Step-by-step explanation:
Mika would need 10 minutes to eat 35 hot dogs.
Mika can eat 21 hot dogs in 6 minutes. So Mika eats 21 hot dogs/6 minutes
So Mika eats 35 hot dogs/m minutes. The proportion is set up like this:
21/6 = 35/m Then, cross-multiply:
6·35 = 21m
m = 210/21
m = 10 minutes
Drag the tiles to the correct boxes to complete the pairs. Match each function to its domain and range.

Answers
Matching of the functions domain and range are as follows:
f(x) = 4-4x ;
Domain:{0,1,3,5,6}
Range;{-20,-16,-8,0,4}
f(x) = 5x - 3
Domain:{-2,-1,0,3,4}
Range:{-13,-8,-3,12,4}
f(x) = -10x
Domain:{-4,-2,0,2,4}
Range:{-40,-20,0,20,40}
f(x) = (3/x) + 1.5
Domain:{-3,-2,-1,2,6}
Range:{0.5,0,-1.5,3,2}.
How to find the domain and range of the functions?1) The function f(x) = 4 - 4x
Take Domain:{0,1,3,5,6}
If, we take x=0 and put in the function then we get
f(x)=4-0
f(x)=4
put x=1
f(x) = 4 - 4 =0
put x=3 then we get
f(x)=4-12=--8
put x=5 them we get
f(x)=4-20=-16
put x=6 then we get
f(x)=4-24=-20
Therefore ,range:[-20,-16,-8,0,4}
2) The function f(x)=5x-3
Take domain{-2,-1,0,3,4}
Now, put x=-2 in the function then we get
f(x) = -13
now put x=-1 then we get
f(x)=-5-3=-8
Put x=0 then we get
f(x)=0-3=-3
Put x=3 then we get
f(x)=15-3=12
Put x=4 then we get
f(x)=20-3=17
Therefore , range:{-13,-8,-3,12,17}
3) The function f(x)=-10x
Take domain:{-4,-2,0,2,4}
Put x=-4 in the function then we get
f(x)=40
Put x= -2 then we get
f(x)=20
Put x=0 then we get
f(x)=0
Put x=2 then we get
f(x)=-20
Put x=4 then we get
f(x)=-40
Therefore , range :{-40,-20,0,20,40}
4) The function f(x)= (3/x) + 1.5
Take domain:{-3,-2,-1,2,6}
Put x= -3 in the taken function then we get
f(x)=-1+1.5=0.5
put x=-2 then we get
f(x)= -1.5+1.5=0
Put x=-1 then we get
f(x)=-3+1.5=-1.5
Put x= 2 then we get
f(x)=1.5+1.5=3
Put x= 6 then we get
f(x)=0.5+1.5=2
Therefore, range : {0.5,0,-1.5,3,2}.
Read more about Domain and Range at: https://brainly.com/question/10197594
#SPJ1
a(n)=−5+6(n−1)
What is the 12th term in the sequence
Answers
Answer:
n/2[2a+(n-1)d]
12/2[2(-5)+(12-1)6]
66-10=56×6=336
336 is the 12th term
12=x÷8
I need help please
Answers
Answer:
x=96
Step-by-step explanation:
I believe that’s the answer
I don’t get it. Can someone explain this to me?

Answers
Answer:
18.285 in.²
Step-by-step explanation:
3 in. × 4 in. = 12 in.²
A = πr²
A = 12.57 in.²
12.57 in.² ÷ 2 = 6.285 in.²
6.285 in.² + 12 in.²
18.285 in.²
-) Aspirin has a half-life of 6 hours in the blood stream. If a person takes 625mg, how long will it take for there to be 150mg left in the bloodstream?
Answers
It will take approximately 25 hours and 1 minute for there to be 150mg of aspirin left in the bloodstream.
We have,
To determine how long it will take for there to be 150mg of aspirin left in the bloodstream, we can use the concept of half-life.
The half-life of aspirin is given as 6 hours, which means that after every 6 hours, the amount of aspirin in the bloodstream reduces by half.
Let's calculate the number of half-lives required to reach 150mg:
Initial amount of aspirin = 625mg
Final amount of aspirin = 150mg
625mg / 150mg = 4.17
This means it will take approximately 4.17 half-lives for the amount of aspirin in the bloodstream to reduce from 625mg to 150mg.
Since each half-life is 6 hours, we can calculate the total time it will take:
Total time = Number of half-lives * Half-life duration
Total time = 4.17 x 6 hours
Total time ≈ 25 hours and 1 minute
Therefore,
It will take approximately 25 hours and 1 minute for there to be 150mg of aspirin left in the bloodstream.
Learn more about expressions here:
https://brainly.com/question/3118662
#SPJ1
Over a half-mile stretch of road, there are 7 evenly spaced street signs. Find the distance
between each street sign.
Answers
Answer:
We know that:
Over a half-mile stretch of road, there are 7 evenly spaced street signs.
If we assume that there is a sign right at the beginning and another right at the end, then the distance between each sign will be equal to the total distance divided by the total number of signs minus one because the distance is measured in pairs of consecutive signs, if we have 7 signs, then we will have 6 pairs of consecutive ones ( 1st and 2nd, 2nd and 3rd, 3rd and 4th, ...)
(0.5mi)/6 = 0.83... mi
So, rounding to the second decimal after the decimal point, the distance between each sign is 0.83 miles.
Find four pairs of integers that add up to 1.
Answers
Answer:
5 & -4
4 & -3
3 & -2
2 & -1
Step-by-step explanation:
5 + (-4) = 1
4 + (-3) = 1
3 + (-2) = 1
2 + (-1) = 1
A 2-gallon container of disinfectant costs $20.48. What is the price per cup?
Answers
Answer:
$0.64 per cup
Step-by-step explanation:
There are 16 cups in 1 gallon, so the number of cups in 2 gallons is:
1 gallon: 16 cups
2 gallon = 2 x 1 gallon = 2 x 16 cups = 32 cups
So we need to find the price of each cup:
1 cup = ($20.48 / 32 cups) = $0.64 per cup.
Does the geometric sequence converge or diverge? Explain.
5,-2.5, 1.25,-0.625,...
O The sequence diverges because r = -2, which is less than 1.
The sequence converges because |r | = 0.5, which is less than 1.
O The sequence diverges because Ir | = 2, which is greater than 1.
O The sequence converges because r = 0.5, which is less than 1.
Answers
In a geometric sequence, each term is obtained by multiplying the previous term by a constant factor called the common ratio (denoted by \(\displaystyle\sf r\)). In the given sequence, the common ratio is \(\displaystyle\sf r=-2\).
To determine if the sequence converges or diverges, we look at the absolute value of the common ratio (\(\displaystyle\sf |r|\)). If the absolute value of the common ratio is less than 1 (\(\displaystyle\sf |r|<1\)), the sequence converges. If the absolute value of the common ratio is greater than or equal to 1 (\(\displaystyle\sf |r|\geq 1\)), the sequence diverges.
In this case, the absolute value of the common ratio is \(\displaystyle\sf |-2|=2\), which is greater than 1. Therefore, the sequence diverges.
Answer:
Step-by-step explanation:
The common ratio in a geometric sequence is calculated by dividing any term by its preceding term. In this case:
-2.5 ÷ 5 = -0.5
1.25 ÷ -2.5 = -0.5
-0.625 ÷ 1.25 = -0.5
We can observe that the common ratio between each term is -0.5.
A geometric sequence converges if the absolute value of the common ratio is between -1 and 1. In this case, the absolute value of the common ratio (-0.5) is less than 1. Therefore, the geometric sequence converges.
In a converging geometric sequence, as more terms are added, the values approach a certain limiting value. In this case, since the common ratio is negative, the terms alternate between positive and negative values. As the sequence progresses, the absolute values of the terms decrease, approaching zero.
Hence, the geometric sequence 5, -2.5, 1.25, -0.625, ... converges.
2(-x-4)+3=-7x+5+5x
Pls help!!!!!!!!
Answers
1 Simplify
−
7
x
+
5
+
5
x
−7x+5+5x to
−
2
x
+
5
−2x+5.
2
(
−
x
−
4
)
+
3
=
−
2
x
+
5
2(−x−4)+3=−2x+5
2 Expand.
−
2
x
−
8
+
3
=
−
2
x
+
5
−2x−8+3=−2x+5
3 Simplify
−
2
x
−
8
+
3
−2x−8+3 to
−
2
x
−
5
−2x−5.
−
2
x
−
5
=
−
2
x
+
5
−2x−5=−2x+5
4 Cancel
−
2
x
−2x on both sides.
−
5
=
5
−5=5
5 Since
−
5
=
5
−5=5 is false, there is no solution.
No Solution
n*2 + 5n +2 (when n= -2)
Answers
Answer:
-12
Step-by-step explanation:
n*2 + 5n + 2
-2 × 2 + 5(-2) + 2
-4 + -10 + 2
= -12
Mean is 22 and standard deviation is 0.2, what is the spread
Answers
Answer:
:v What??
jwkwlwmwbwjqkq
.........
.
........
..

Answer:
0.04
Step-by-step explanation:
Standard deviations== square root of variance define as spread.
Standard deviations square = variance
[0.2]^2= 0.04