Veronika’s five test scores are 59, 80, 95, 88, and 93. If the outlier of 59 is removed, what is the mean absolute deviation of the remaining four test scores
Answers
Answer:
Mean deviation of 80, 88, 93, 95 is 5
Step-by-step explanation:
Step 1: find the mean
Mean = Sum of items/ Number of items
Mean = 80+88+93+95 = 356
Mean = 356 / 4 = 89
Step 2: find the mean deviation
Mean Deviation = ∑i = 0n |xi − μ| / N
Mean Deviation = | (89-80) + (89-88) + (89-93) + (89-95) | /4
Mean Deviation = 5
Related Questions
A rectangle with vertices M(-7, -2), N(-5, -1), O (-2, -7) and P(-4, -8) is rotated 90 degrees counter clockwise about the origin. What are the new locations of the vertices?
Answers
Answer: If the figure is rotated 90 degrees counter clockwise about the origin, ... Triangle LMN has vertices L(-1,4), M(-2,4), and N(-1,-1).
Step-by-step explanation:
90 Degrees
Show that 1/x is an integrating factor of the equation dy/dx-y/x = 3x
Answers
Suppose we're asked to solve the first order linear differnetial equation,
\(\longrightarrow\rm{\dfrac{dy}{dx}+y\cdot P(x)=Q(x)}\)
To solve this equation we have to find out a term called 'Integrating Factor' given by,
\(\rm{I_f=e^{\int P(x)\ dx}}\)
such that the solution of the equation is,
\(\displaystyle\longrightarrow\rm{y\cdot I_f=\int Q(x)\cdot I_f\ dx}\)
Here the given differential equation is,
\(\longrightarrow\rm{\dfrac{dy}{dx}-\dfrac{y}{x}=3x}\)
\(\longrightarrow\rm{\dfrac{dy}{dx}+y\left(-\dfrac{1}{x}\right)=(3x)}\)
Here,
\(\longrightarrow\rm{P(x)=-\dfrac{1}{x}}\)
Integrating wrt x,
\(\displaystyle\longrightarrow\rm{\int P(x)\ dx=-\int\dfrac{1}{x}\ dx}\)
\(\displaystyle\longrightarrow\rm{\int P(x)\ dx=-\ln|x|}\)
[We will consider constant of integration as zero.]
Then the integrating factor is,
\(\longrightarrow\rm{I_f=e^{\int P(x)\ dx}}\)
\(\longrightarrow\rm{I_f=e^{-\ln|x|}}\)
Since \(\rm{e^{b\,\ln(a)}=a^b,}\)
\(\longrightarrow\rm{I_f=x^{-1}}\)
\(\longrightarrow\rm{\underline{\underline{I_f=\dfrac{1}{x}}}}\)
Hence the integrating factor for the given differential equation is 1/x.
Using a graph, table of values, and/or equations solve the following problem.
When 1 is subtracted from six times a certain number, the result is 21. What is the number?
Round and write your answer to the tenths place value. Do not include units
Answers
Answer:
n = 11/3
Step-by-step explanation:
n = certain number
6n - 1 = 21
6n = 22
n = 22/6 or 11/3
Proof that 1^√2 = 1 is true
Answers
Answer:
1^sqrt(2) = 1 is always true
Step-by-step explanation:
Step-by-step explanation:
it is always 1 because the teacher said.....lol
(s3-6s)+4t2 when s=5 and 3=t
Answers
Answer:
9
Step-by-step explanation:
(5)3-6(5)+4(3)2
(15-30)+4(3)2
-15+ 24
=9
Q3: Solve the following first order differential equation using Exact method (e^{y+x} + ye^y)dx + (xe^y-1)dy , y(0) = -1
Answers
To solve the differential equation using the exact method, we need to verify that it is exact. A first-order differential equation of the form M(x,y)dx + N(x,y)dy = 0 is exact if and only if ∂M/∂y = ∂N/∂x.
In this case, we have:
M(x,y) = e^{y+x} + ye^y
N(x,y) = xe^y - 1
∂M/∂y = e^{y+x} + e^y + ye^y
∂N/∂x = e^y
Since ∂M/∂y is not equal to ∂N/∂x, the equation is not exact. However, we can make it exact by multiplying both sides of the equation by a suitable integrating factor. An integrating factor is a function that when multiplied by both sides of a differential equation, makes it exact.
To find the integrating factor, we need to find a function μ(x,y) such that:
μ(x,y)∂M/∂y - ∂μ/∂y M(x,y) = μ(x,y)∂N/∂x - ∂μ/∂x N(x,y)
By comparing the coefficients of dx and dy, we get:
∂μ/∂y = xe^y - 1
∂μ/∂x = e^{y+x} + ye^y
Integrating the first equation with respect to y and the second equation with respect to x, we get:
μ(x,y) = e^{xy} - y
μ(x,y) = e^{y+x} + ye^y + f(x)
Equating the two expressions for μ(x,y), we get:
e^{xy} - y = e^{y+x} + ye^y + f(x)
Taking the derivative of both sides with respect to x, we get:
ye^{xy} = e^{y+x} + ye^y f'(x)
Solving for f'(x), we get:
f'(x) = \frac{ye^{xy}-e^{y+x}}{ye^y}
Integrating both sides with respect to x, we get:
The solution of the first order differential equation using Exact method is -e⁻¹
We must determine whether the differential equation meets the criteria for being exact in order to solve it using the exact method, which is given by:
∂M/∂y = ∂N/∂x
where M and N, respectively, are the dx and dy coefficients.
Here, \(M = e^{y+x} + ye^y\) and\(N = xe^y - 1.\)
∂M/∂y = \(e^{y+x} + e^y + ye^y\)
∂N/∂x = \(e^y\)
We must discover the integrating factor to make the equation precise because ∂M/∂y does not equal ∂N/∂x. The formula for the integrating factor is
μ =\(e^{\int\limits(\partial N/\partial x - \partial M/\partial y)/N dx = e^{\int\limits(1 - e^{-y})/x dx} = e^y ln|x|\)
We obtain the following by multiplying the given equation by the integrating factor:
\((e^{2y+x}ln|x| + ye^yln|x|)dx + (xe^yln|x| - ln|x|)dy = 0\)
We can now check if the equation is exact:
∂M/∂y = \(e^{2y+x}ln|x| + e^y + ye^yln|x|\)
∂N/∂x = \(e^yln|x|\)
As both are equal, the equation is exact.
By integrating the coefficients of dx with respect to x and dy with respect to y, we can now get the potential function u(x,y):
u(x,y) = ∫\((e^{2y+x}ln|x| + ye^yln|x|)dx = x e^{2y+x} ln|x| - x ye^yln|x| + f(y)\)
∂u/∂y = \(xe^{2y+x} + e^yln|x| + ye^y\)
Comparing this with N, we get:
∂u/∂y = ∫Ndy = ∫\((xe^y-1)dy = xe^y - y + g(x)\)
Using u's partial derivative with regard to y, we can calculate:
\(xe^{2y+x} + e^yln|x| + ye^y = xe^y + g'(x)\)
Comparing the coefficients of \(e^y\) and ln|x|, we get:
g'(x) = \(xe^{2y+x} - ye^y\)
When we combine both sides in relation to x, we get:
g(x) = \((1/3)xe^{2y+3x} - xye^y + C\)
where C is the integration constant.
When we change the values of u and g in the formula u(x,y) = g(x) + C, we obtain:
\(x e^{2y+x} ln|x| - x ye^yln|x| + (1/3)xe^{2y+3x} - xye^y = C\)
Substituting the initial condition y(0) = -1, we get:
C = -e⁻¹
As a result, the following is the differential equation's solution:
\(x e^{2y+x} ln|x| - x ye^yln|x| + (1/3)xe^{2y+3x} - xye^y = -e^{(-1)\)
To know more about differential equation, refer here:
brainly.com/question/14598404#
#SPJ11
Express (root 19 - root 7)(root 19 + root 7) in simplest form.
Answers
Answer
root 354
Step-by-step explanation:
Answer:
12
Step-by-step explanation:
(√19 -√7)(√19 +√7)
( a +b)( a -b) = a²-b²
(√19)² -(√7)² = 19 -7 = 12
Use the table below to find what the out put will be when the input is 54. Explain

Answers
Answer:
The answer is 15
Step-by-step explanation:
adding 3 to y for each time 1 is added to y. since you start with a base of 9, we can conclude this answer by taking 3 times 15, which is 45, then adding 9, which makes 54. Like this:
0 | 9
1 | 12
2 | 15
...
13 | 48
14 | 51
15 | 54
Use the inteediate value theorem to show that there is a root (a point where f(x))=(0) for the equation f(x)=x^(5)-2x^(3)-2. Make sure to show all your work and explain how all the requirements are met.
Answers
The equation f(x) = x^5 - 2x^3 - 2 has a root in the interval [-2, 0] by the Intermediate Value Theorem.
To apply the Intermediate Value Theorem and show that there is a root (a point where f(x) = 0) for the equation f(x) = x^5 - 2x^3 - 2, we need to demonstrate that f(x) changes sign over a given interval.
First, we evaluate f(x) at two points, a and b, such that f(a) and f(b) have opposite signs. Let's choose a = -2 and b = 0:
f(-2) = (-2)^5 - 2(-2)^3 - 2 = -18
f(0) = (0)^5 - 2(0)^3 - 2 = -2
Since f(-2) = -18 is negative and f(0) = -2 is positive, f(x) changes sign over the interval [-2, 0]. According to the Intermediate Value Theorem, there must exist at least one value c within this interval where f(c) = 0, indicating the presence of a root.
Therefore, by satisfying the requirements of the Intermediate Value Theorem and showing a change in sign between f(-2) and f(0), we can conclude that there is a root for the equation f(x) = x^5 - 2x^3 - 2 within the interval [-2, 0].
learn more about "equation ":- https://brainly.com/question/29174899
#SPJ11
3 ?
-
5 = 20
3 fifths is equivalent to what 20s
Answers
Answer:
3 12
- = -
5 20
Step-by-step explanation:
5×4=20
3×4= 12
The graphs below have the same shape. What is the equation of the blue
graph?
g(x) =____
f(x) = x² 5
-5
-5
O A. g(x) = (x + 2)²
OB. g(x)=(x-2)²
O c. g(x)²2-2.
OD. g(x)=x² +21
X
g(x) = ?
5

Answers
Answer:
B
Step-by-step explanation:
given f(x) then f(x ± a ) is a horizontal translation of f(x)
• if + a , then a shift left of a units
• if - a then a shift right of a units
here g(x) is the graph of f(x) moved 2 units right , then
g(x) = (x - 2)²
Shop A has repaired 55 cars and repairs
5 more each week. Shop B has repaired
30 cars and repairs 10 more each week.
How many weeks (w) will it be before
Shop B repairs as many cars (C)
as Shop A?
C5W + 55
C= 10W + 30
Answers
Using a system of equations, it will take 5 weeks for Shop B to repair as many cars as Shop A.
What is a system of equations?A system of equations is called simultaneous equations.
Simultaneous equations are two or more equations solved concurrently.
Shop A Shop B
The number of cars already repaired 55 30
The number of cars repaired per week 5 10
Let the number of cars repaired by Shop A in w weeks = 5w + 55
Let the number of cars repaired by Shop B in w weeks = 10w + 30
For the number of cars repaired by each shop to equate, 5w + 55 = 10w + 30
5w - 10w = 30 - 55
-5w = -25
w = 5
Thus, using simultaneous equations, we can conclude that it will take Shop B 5 weeks to repair as many cars as Shop A.
Learn more simultaneous equations at https://brainly.com/question/148035
#SPJ1
Plss answer all these showing your work need the answers asap will give the first person that answers all and shows work brainliest, don’t give me no files

Answers
Answer:
Subtract everything from 180. The square boxes represent 90°.
1. 180-80-40 = 60°
2. 180-90-32 = 58°
3. 180-45-90 = 45°
4. 180-90-78 = 12°
5. 180-90-15 = 75°
6. 180-55-25 = 100°
7. 180-90-36 = 54°
8. 180-90-30 = 60°
9. 180-60-30 = 90°
Hope this helped :)
A street performer earns 45% of all of his daily earnings at the Barclays Center subway station. He earns about $300 daily. How much does he earn at the Barclays Center subway station?
Answers
Answer:
666
Step-by-step explanation:
Jane has 1 quarter, 3 dimes, and 4 nickels. What percent of dollar does Jane have?
i know the answer is 44% but can someone please explain how i got 44%??
Answers
Answer:
ok so I'm English not a hundred percent sure on your break down of money......so if I'm right in thinking that a nickel = 5 cents, dime = 10cents and a quarter =25cents
you add the amounts together
so 25 + 30 +20 = 75 cents.
there are 100 cents in a dollar so 100/100 X 75=75%
I have no idea how you got to 44%
Which value of x means that 3x < 2x + 1
Answers
Answer:
The answer is: x < 1
Step-by-step explanation:
the time spent waiting in the line is approximately normally distributed. the mean waiting time is 44 minutes and the standard deviation of the waiting time is 22 minutes. find the probability that a person will wait for more than 66 minutes. round your answer to four decimal places.
Answers
The probability that a person will wait for more than 66 minutes is 0.1587
Given;
The time spent waiting in line is approximately normally distributed with the mean will be ' X '.
The mean given is μ = 44 minutes
The standard deviation is δ = 22 minutes
The probability that a person will wait for more than 66 minutes is;
P ( X > 66 ) = P [ X - μ/δ > 66 - μ/δ]
= P [Z > 66 - 44 / 22]
= P [Z > 1]
= 1 - P(Z ≤ 1)
= 1 - 0.8413
= 0.1587
The probability that a person will wait for more than 66 minutes is 0.1587.
To learn more about Probability click here:
brainly.com/question/11234923
#SPJ4
if 2/5 of the sweets in a bag is 60, how
many sweets would represent 1/3
Answers
Answer:
50 Candy
Step-by-step explanation:
We know that 2/5 of the bag is 60 candy. By taking this information we can conclude that 1/5 of the bag is 30 candy. We know that 1/5 of the bag is 30, so 30 times 5 is 150 candy.
Now that we have found out that there is 150 candy total we can know divde 150 by 3 to find out how much candy is in 1/3 of the bag.
150/3 = 50 Candy
1/3 of the bag represent 50 candy.
what primary characteristics distinguish a spatial join from selecting by location? from the intersect function?
Answers
Spatial join, selecting by location, and intersect function are all used in GIS to combine or extract spatial information from multiple layers. The primary characteristics that distinguish a spatial join from selecting by location and intersect function are:
Spatial Join: A spatial join combines two or more layers based on their spatial relationship. It creates a new layer by linking attributes from one layer to another based on the spatial relationship between the features. For example, a spatial join can be used to find out how many houses are within a certain distance from a park.Selecting by Location: Selecting by location is used to extract features from one layer that intersect with features from another layer. It creates a new layer with the selected features only. For example, selecting by location can be used to find out which buildings intersect a flood zone.Intersect Function: The intersect function creates a new layer by overlaying two or more layers and only keeping the areas where they intersect. For example, the intersect function can be used to find out which parcels of land intersect with a road, and then create a new layer with those parcels only.In summary, the primary characteristic that distinguishes a spatial join from selecting by location and intersect function is that a spatial join combines layers based on their spatial relationship, while selecting by location and intersect function extract features based on their spatial relationship.
For more details about information click here:
https://brainly.com/question/13629038#
#SPJ11
Help me answe this please lol
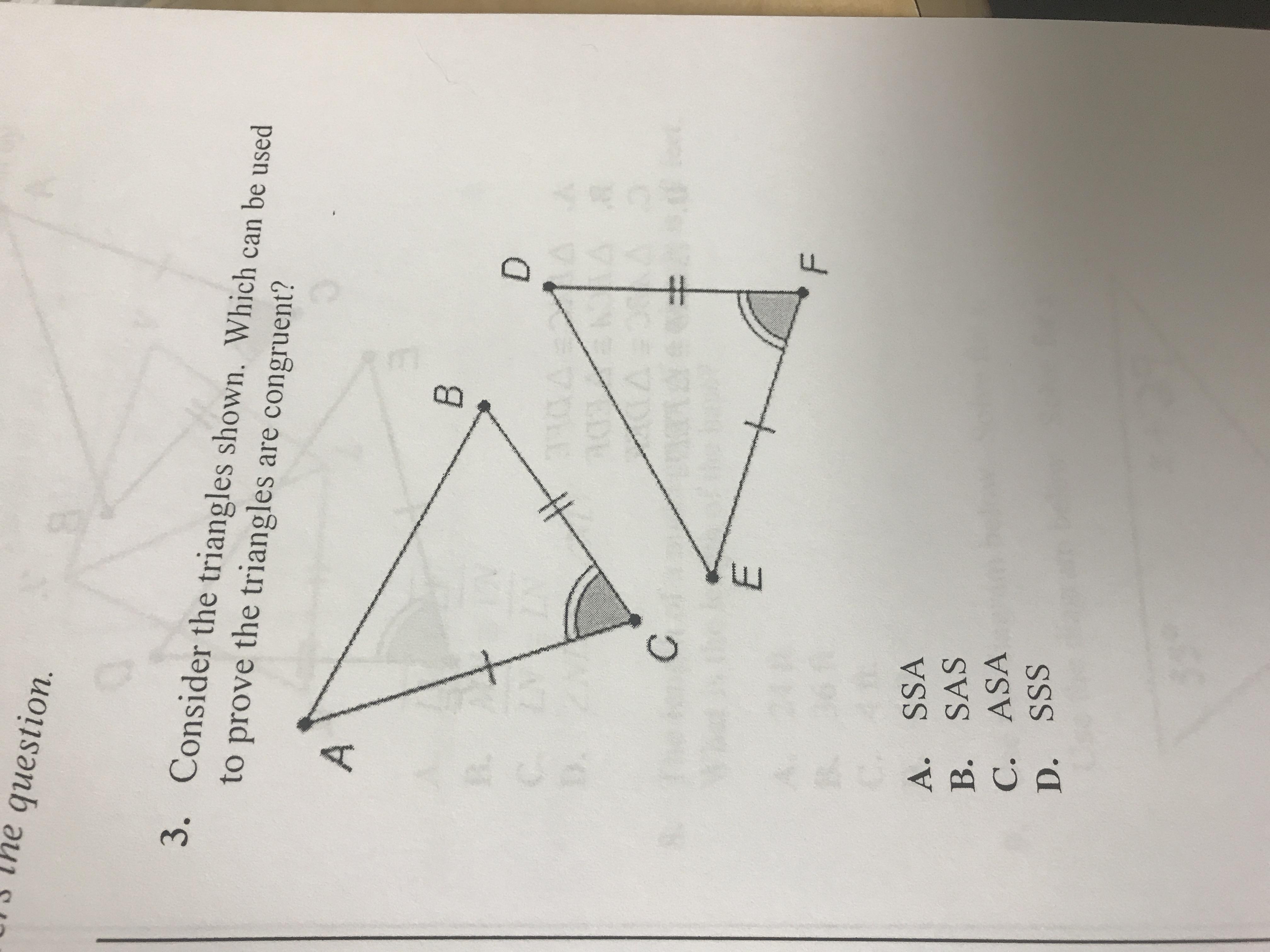
Answers
Answer:
SAS
is the correct answer of this question
Answer:
SAS
Step-by-step explanation:
SAS is an abbreviation for side angle side, which is what your triangle shows.
whats is the measure of x
Answers
Worth 60 points for a rapid reply- find the area of each regular polygon. Answers are rounded to the nearest whole number.

Answers
The area of the regular polygons with 12 sides(dodecagon) and 5 sides (pentagon) are 389.06 in² and 19.87 in² respectively.
How to calculate for the area of the polygonArea of regular polygon = 1/2 × apothem × perimeter
perimeter = (s)side length of octagon × (n)number of side.
apothem = s/[2tan(180/n)].
11 = s/[2tan(180/12)]
s = 11 × 2tan15
s = 5.8949
perimeter = 5.8949 × 12 = 70.7388
Area of dodecagon = 1/2 × 11 × 70.7388
Area of dodecagon = 389.0634 in²
Area of pentagon = 1/2 × 5.23 × 7.6
Area of pentagon = 19.874 in²
Therefore, the area of the regular polygons with 12 sides(dodecagon) and 5 sides (pentagon) are 389.06 in² and 19.87 in² respectively.
Read more about area here:https://brainly.com/question/27440983
#SPJ1
What is 124 lbs in kg ?
Answers
Answer: 56.24545388
Step-by-step explanation:
A common question is How many pound in 124 kilogram? And the answer is 273.373205109 lbs in 124 kg. Likewise the question how many kilogram in 124 pound has the answer of 56.24545388 kg in 124 lbs.
By converting 124 pound to kilogram has the answer of 56.24545388 kg in 124 lbs.
How to convert pound to kilogram ?To convert 124 lbs to kg multiply the mass in pounds by 0.45359237. The 124 lbs in kg formula is [kg] = 124 * 0.45359237. Thus, for 124 pounds in kilogram we get 56.24545388 kg.
The fundamental mass unit in the metric system is the kilogramme (kg). The mass of 1,000 cubic centimetres of water is very close to (and was originally intended to be exactly) one kilogramme. The actual weight of a pound is 0.45359237 kg.
In its initial form, a solid platinum cylinder served as the kilogram's symbol in the late 18th century. However, it turned out to be difficult and cumbersome to measure the mass of a volume of water, thus the platinum artefact itself ended up being the standard. It was replaced in 1889 by a standard kilogramme, which was constructed of the same platinum-iridium alloy as the bar being used at the time to define the metre and was also a solid cylinder with a height equal to its diameter.
To know more about diameter visit:-
https://brainly.com/question/28544190
#SPJ4
If a,b,c and d are the digits at the thousand,hundreds,tens,and ones place respectively.Write the number formed by these digits.
Answers
Answer:
1000a+100b+10c+d
Step-by-step explanation:
place value of a =1000×a
place value of b=100×b
place value of c=10c
place value of d=1×d
Determine which function has the greatest rate of change as x approaches infinity.A). f(x) = 2x − 8B). g(x) = 5x^2 − x + 7C). h(x) = 4^x − 6D). There is not enough information to determine the answer.
Answers
We need to find the derivative which is the rate of change
\(\begin{gathered} f^{\prime}(x)=2 \\ g^{\prime}(x)=10x\text{ - }1\text{ + 7} \\ g^{\prime}(x)=10x+6 \\ h^{\prime}(x)=4 \end{gathered}\)So, when x is infinite, the function g(x) has the greatest rate of change
Find the sum. Write your answer in standard form. (2x3+4x2+3)+(3x3−3x−4)
Answers
Answer:
5x³ + 4x² - 3x - 1
General Formulas and Concepts:
Algebra I
Terms/CoefficientsStep-by-step explanation:
Step 1: Define
Identify
(2x³ + 4x² + 3) + (3x³ - 3x - 4)
Step 2: Simplify
Combine like terms: 5x³ + 4x² - 3x - 1Answer:
\(3.8*10^1\)
Step-by-step explanation:
So we'll be using PEMDAS, which is an acronym used to explain order of operations. It stands for P- Parentheses, E- Exponents, M- Multiplication, D- Division, A- Addition, and S- Subtraction.
P- Parentheses:
(2x3+4x2+3)+(3x3−(3x−4))
M- Multiplication (within Parentheses):
(6+8+3)+(9−(-12))
A- Addition (within Parentheses):
(6+8+3)+(9−(-12))
17 + 21
A- Addition:
38
Now, we'll take that number and put it in standard form, which is the number with only one number outside of the decimal times ten to the however many times it can be divided by ten.
So,
38/10 = 3.8
So,
3.8 * 10^1 is your answer.
PLEASE HELP ME!!!!!!!
The number of lattes sold daily by two coffee shops is shown in the table.
Shop A Shop B
55 36
52 40
50 34
47 39
51 44
48 41
53 40
53 38
Based on these data, is it better to describe the centers of distribution in terms of the mean or the median?
a. Mean for both coffee shops because the data distribution is symmetric
b. Median for both coffee shops because the data distribution is not symmetric
c. Mean for shop B because the data distribution is symmetric; median for shop A because the data distribution is not symmetric
d. Mean for shop A because the data distribution is symmetric; median for shop B because the data distribution is not symmetric
Answers
Based on data, it is better to describe the centers of distribution in terms of median because the data distribution is not symmetric. The Option B is correct.
What is a better measure of center for the given data?To determine a better measure of center, we must examine the symmetry of the data distribution. We can do it by constructing box plots or dot plots but because we have small data set, we will examine the data visually.
By looking at the data, we see that those distributions are not perfectly symmetric with some values have more spread out than the others. So, it is better to describe the centers of distribution in median rather than in mean.
Read more about median
brainly.com/question/26177250
#SPJ1
We can learn a lot about a population if we select a ______ of it. Group of answer choices population subset data set case
Answers
We can learn a lot about a population if we select a subset of it.
What is a subset?One kind of set is a sample space. It is a clear listing of every event that could occur in a statistical experiment. A statistical experiment's events are a subset of the sample space.
A subset is a smaller group of results that are part of the bigger group.
Subsets are events, and events are subsets. A subset is an event of a sample space, and an event is a potential result of an experiment. A random experiment's sample space is a set (S) that contains all of the experiment's potential outcomes.
Learn more about subsets here:
https://brainly.com/question/20509970
#SPJ4
what do you call the fixed line of a parabola?
Answers
Answer: directrix.
hoped this helped lmk if it did
How many solutions does this system have?
Y= 3x+2
Y= 3x-6
Answers
Answer:
None
Step-by-step explanation:
They have the same slope so they are parallel and will never intersect.
Answer:
No solutions
Step-by-step explanation:
I just did it on Khan Academy.