Vincent bought a 25-pound bag of rice. He cooked 6.25 pounds of the rice. He stored the rest of the rice in 334 - pound portions. What is the maximum number of 334 - pound portions he stored?
Answers
Question:
Vincent bought a 25-pound bag of rice. He cooked 6.25 pounds of the rice. He stored the rest of the rice in \(3\frac{3}{4}\) - pound portions. What is the maximum number of \(3\frac{3}{4}\) - pound portions he stored?
Answer:
The maximum number of portion he stored is 5 portion
Step-by-step explanation:
Given
Size of Rice = 25 lb
Size of Cooked Rice = 6.25 lb
Portions saved = \(3\frac{3}{4}\) lb
Required
Number of portion saved;
First, the size of rice after cooking needs to be calculated;
If 6.25lb of rice was cooked from a total of 25lb;
Then, the size of rice left is
\(Size = 25lb - 6.25lb\)
\(Size = 18.75lb\)
Now that we have the amount left after cooking; we can simply calculate the maximum number of portions;
This is calculated by dividing size of rice left by portions of saved rice;
i.e.
Maximum number of portion = Size of rice left / Portions of saved rice
Maximum number of portion = \(\frac{18.75lb}{3\frac{3}{4}lb}\)
Convert \(3\frac{3}{4}\) to mixed fraction
Maximum number of portion = \(\frac{18.75lb}{\frac{15}{4}lb}\)
Maximum number of portion = \(\frac{18.75}{\frac{15}{4}}\)
Rewrite expression
Maximum number of portion = \(18.75 / \frac{15}{4}\)
Change divide (/) sign to multiplication (*)
Maximum number of portion = \(18.75 * \frac{4}{15}\)
Maximum number of portion = \(\frac{75}{15}\)
Maximum number of portion = 5
Hence, the maximum number of portion he stored is 5 portions
Related Questions
f(x)= x+6x 2+9x+18
g(x)=x+3
Determine whether or not the two functions are equal. Provide a supporting explanation for your determination. Your explanation can be verbal, symbolic, graphical, or numerical. Grading: /10 /2 points for correctly identifying whether or not the functions are equal ( 1 point for identifying an answer. 2 points for identifying the correct answer) 14 points for your supporting explanation (1=little or no supporting details or major conceptual misunderstanding. 2= supporting details are vagup or have multiple flaws in reasoning. 3= supporting details are given, but some details are missing or are invalid. 4=
Answers
The two functions, F(x) = x + 6x^2 + 9x + 18 and g(x) = x + 3, are not equal.
In F(x), the highest power of x is x^2, while in g(x), the highest power of x is x^1. This difference alone indicates that the functions are not equal since their terms involve different powers of x.
To further demonstrate this, let's simplify and compare the two functions. Expanding F(x), we have F(x) = 6x^2 + (1+9)x + 18 = 6x^2 + 10x + 18. On the other hand, g(x) remains unchanged as x + 3.
If the two functions were equal, their corresponding terms would have to be equal. However, looking at the simplified forms, we can see that the coefficients of the x^2 terms (6 in F(x)) are different from each other, and the constant terms (18 in F(x) and 3 in g(x)) are also different. Hence, the two functions are not equal.
In summary, the functions F(x) = x + 6x^2 + 9x + 18 and g(x) = x + 3 are not equal because their terms involve different powers of x and have different coefficients.
Learn more about functions here:
https://brainly.com/question/31062578
#SPJ11
please no links!!!!!!!!!!!
Suppose a trip is 355.1 miles long and you want to spend 2 days driving. How many miles
should you drive each day?
Answers
Answer: 177.55 miles
Step-by-step explanation: 355.1/2
= 177.55 miles each day
Answer:
177.55mi/day
Step-by-step explanation:
If you travel for x number of days and want to split your trip evenly across those days, simply divide the distance you need to travel by the number of days.
HELP PLEASE PLEASE PLEASEEEEEEEEE!!!!!

Answers
Answer:
x = 70 degrees
Step-by-step explanation:
Answer:
x = 70°
Step-by-step explanation:
Because it is an isosceles triangle, the two base angles are the same (55° and 55°)
All triangles angles must add up to 180°, so 180-55-55 will give us the missing angle (x).
180-55-55 = 70
x = 70°
Approximately how much greater, in grams is 191520 than 146640
Answers
Find the 73rd term of the following arithmetic sequence. 7, 12, 17, 22,
Answers
Answer:
\(a_{73}=367\)
Step-by-step explanation:
\(a_n=a_1+(n-1)d\\a_{73}=7+(73-1)(5)\\a_{73}=7+(72)(5)\\a_{73}=7+360\\a_{73}=367\)
PLEASE HURRY!!! What is the value of p in the equation?
One-fourth (8 minus 4 p) + 2 p = 12 Here are the answer choices...
–20
–2
5
10
Answers
Answer:
10
Step-by-step explanation:
took the test on edge
Solve the following by completing the square y=x^2+10
Answers
The resulting equation on using the completing the square is y = (x+5)² - 25
Completing the square methodThe quadratic equation has a leading degree of 2. Given the equation below;
y = x^2+10x
Add the square of the half of coefficient of x to have;
y = x^2+10x + (10/2)²- (10/2)²
y = x^2 + 10x + 5² - 5²
y = x^2 + 10x + 25 - 25
y = (x+5)² - 25
Hence the resulting equation on using the completing the square is y = (x+5)² - 25
Learn more on completing the square here: https://brainly.com/question/1596209
#SPJ1
Find the equation of a line perpendicular to y - 1= -x that passes through the
point (-4,-8).
1.) y = x - 4
2.) y = -x - 4
3.) y = -x - 1
4.) y = x - 1
Answers
Answer:
4
Step-by-step explanation:
firstly you separate y
y=-x-1
which means that the slope is equal to -1
then you flip the slope so -1 over -1 which is equal 1
Ron Fortini received a 5.20% merit increase and
a 2.75% cost-of-living increase after his quarterly review.
His new weekly salary was $968.80. What was his weekly
salary prior to the increases?
Answers
A salary is the amount of money that an employee receives from their employer each month, particularly if they work in a profession like education, law, or medical
His weekly salary prior to the increases is $897.45.
How to find his salary prior?An employee's pay is the amount of money that they are given each month by their employer, particularly if they work in an occupation like education, law, or medicine.
For instance, the lawyer received a big salary.
Given,
Ron Fortini received a 5.20% merit increase
2.75% cost-of-living increase
His new weekly salary is $968.80.
Solution:
Let's take his initial salary as x.
The total increase in Ron's salary = 5.20%+2.75% = 7.95%
i.e.,
107.95% * x = $968.80
107.95/100*x = 968.80
x = 968.80 * 100/107.95
x = 897.45
His weekly salary prior to the increases is $897.45.
To learn more about salary sums, refer
https://brainly.com/question/25307637
#SPJ13
the chance of rain is forecast to be 20% each day over the next 7 days. how many rainy days should be expected?
Answers
Answer:
The forecasted 20% chance of rain represents the probability of rain on any given day. This does not mean that exactly 20% of the days will have rain, but rather each day independently has a 20% chance of rain.
To calculate the expected number of rainy days over the next 7 days, you can multiply the total number of days (7) by the probability of rain on any given day (0.20 or 20%).
So, the expected number of rainy days is 7 * 0.20 = 1.4 days.
This, of course, is a statistical average. In reality, you can't have 1.4 days of rain - you'll either have 1 day, 2 days, or some other whole number of days. But on average, over many sets of 7-day periods, you'd expect about 1.4 days to have rain.
Which of the following is the graph of f(x) = x2 + 3x − 4? graph of a quadratic function with a minimum at 2, negative 9 and x intercepts at negative 1 and 5 graph of a quadratic function with a minimum at 3, negative 4 and x intercepts at 1 and 5 graph of a quadratic function with a minimum at 2.5, negative 2.4 and x intercepts at 1 and 4 graph of a quadratic function with a minimum at negative 1.5, negative 6.2 and x intercepts at 1 and negative 4
Answers
Answer:
x intercepts at -4 and 1,
with a minimum at (-1.5, -6.25)
Step-by-step explanation:
(x + 4)(x - 1) = 0
x = -4, 1
min = -b/2a = -3/2(1) = x = -1.5
y = (-1.5)² + 3(-1.5) - 4 = -6.25
Answer:
graph of a quadratic function with a minimum at negative 1.5, negative 6.2 and x intercepts at 1 and negative 4
Step-by-step explanation:
The graph shows the minimum is (-1.5, -6.25) and the x-intercepts are a -4 and 1. This matches the last description.
__
The x-coordinates of the offered minima are all different, so it is sufficient to know that the axis of symmetry is the line ...
x = -b/(2a) = -3/(2(1)) = -1.5 . . . . . . . for quadratic f(x) = ax² +bx +c
This is the x-coordinate of the minimum.

Glen Davis is shooting free throws. Making or missing free throws doesn't change the probability that he will make his next one, and he makes his free throws 74%
Answers
Answer:
0.00456
Step-by-step explanation:
Given: Percentage of free throws = 74%
Required: What is the probability of Glen Davis making none of his next 4 free throw attempts?
Since, there is a free throw 74% of the time, thus, the time he misses = 26% of the time.
To miss four in a row, it is requires to miss the first throw, the second throw, the third throw and also the fourth throw.
Thus, the probabilities of Gien missing will be multiplied.
By using the probability formula -
P ( MMMM) = 26/100 × 26/100 × 26/100 × 26/100
= 456976/ 100000000
= 0.00456
Therefore, the probability that he will have next 4 free attempts is 0.00456.
Mr. Keller bought 5 electronic games. The games range from $25. 00 to $65. 00 for each game. What is a reasonable estimate of the amount he paid for the games?
between $25 and 565
between $70 and $120
between $165 and $285
between $290 and $370
Answers
The cost of 5 electronic games falls between $165 and $285.
Mr. Keller bought 5 electronic games, and the games range from $25 to $65 for each game.
We need to find a reasonable estimate of the amount he paid for the games.
Let's find the average value of the games. Add up the cost of each game and divide by the number of games:
The amount for 5 games = (25 + 30 + 35 + 55 + 65) dollar
Amount for 5 games = 240 dollars
Therefore, we can say that the reasonable estimate of the amount he paid for the games is between $165 and $285 dollars. This is because the cost of 5 electronic games falls in between the given values. Hence, option (c) between $165 and $285 is the correct answer.
Option (c) is the correct option: between $165 and $285.
To learn more about cost click on the given link:
https://brainly.com/question/25109150
#SPJ11
Explore equivalent ratios by using the slider. Complete the sentences below. For every __ apples, there are 6 oranges.
Answers
Answer:
For every 2 apples, there are 6 oranges
Step-by-step explanation:
I got it on khan so trust me
(P. S. could u give me brainliest?)
You plan to purchase a house for 12.5 million baht, using a 30-year mortgage. You will make a down payment of 15 percent of the purchase price and you will not pay off the mortgage early. Ignore taxes in your analysis. Your bank offers you the following two options for payment.
Option 1: Mortgage rate of 7.25 percent and zero points.
Option 2: Mortgage rate of 6.75 percent and 4 points.
You would choose option ------- (1 or 2) because the Net Present Value of choosing option 2 is------ . (The answer can be negative. Do not round intermediate calculations and round your answer to two decimal places, e.g., 32.16.)
Answers
Option 2 has a lower NPV and thus should be chosen as it results in less total payment and better savings. Hence, you would choose option 2 as the Net Present Value of choosing option 2 is -9,903,615.48.
Given:
Purchase price = 12.5 million baht
Down payment = 15%30-year mortgage
We have to calculate the option which is best for us.
Option 1: Mortgage rate = 7.25%
Option 2:Mortgage rate = 6.75%
(a) Monthly Payment of Option 1:
Loan Amount = 12.5 * (100-15)%
= 10,625,000 baht
n = 30 * 12
= 360
i = 7.25%/12
= 0.006042857
Yearly Interest Paid = i * 10,625,000
= 64,515.48 baht
Monthly Interest Paid = 64,515.48 / 12
= 5,376.29 baht
EMI =\([P x R x (1+R)^n] / [(1+R)^n-1]\)
where P = Loan Amount, R= Interest Rate per month, n= total number of payments.
EMI = \([10,625,000 x 0.006042857 x (1+0.006042857)^360] / [(1+0.006042857)^360-1]\)
EMI = 69,677.31 baht
(b) Monthly Payment of Option 2:
Loan Amount = 12.5 * (100-15)%
= 10,625,000 baht
n = 30 * 12 = 360
i = 6.75%/12 = 0.005625
Yearly Interest Paid = i * 10,625,000
= 59,765.63 baht
Monthly Interest Paid = 59,765.63 / 12
= 4,980.47 baht
Point cost = 4% of Loan Amount
= 10,625,000 x 4/100
= 425,000 baht
Loan Amount after Deducting Points = 10,625,000 - 425,000
= 10,200,000 baht
EMI = \([P x R x (1+R)^n] / [(1+R)^n-1]\)
where P = Loan Amount, R= Interest Rate per month, n= total number of payments.
EMI =\([10,200,000 x 0.005625 x (1+0.005625)^360] / [(1+0.005625)^360-1]\)
EMI = 66,128.92 baht
(c) We have to calculate the NPV of the payments to decide which option is better.
We use the formula to calculate NPV:-
NPV = - \([B + (PMT / i) * (1 - (1 + i)^-n)] / ((1 + i)^t)\)
Where B = amount borrowed, PMT = monthly payment, i = interest rate, n = total number of payments, t = year.
NPV =\(- [10625000 + (69677.31 / 0.006042857) * (1 - (1 + 0.006042857)^-360)] / ((1 + 0.006042857)^30)\)
= -9,892,571.85 baht
NPV = \(- [10200000 + (66128.92 / 0.005625) * (1 - (1 + 0.005625)^-360)] / ((1 + 0.005625)^30)\)
= -9,903,615.48 baht
Know more about the Net Present Value
https://brainly.com/question/13228231
#SPJ11
Patrick is excited to attend his son’s soccer game tomorrow
evening, but he also needs to ensure his daughter arrives at her
coding class on time. Patrick is debating whether taking the train
or his
Answers
Personal car would be the best option to manage both tasks efficiently. While the train is a reliable mode of transportation, it may have fixed schedules that might not align perfectly with Patrick's needs.
On the other hand, using his personal car provides more flexibility and allows him to tailor the departure time according to his daughter's coding class schedule.
If Patrick decides to take the train, he would need to check the train schedule to see if there are convenient departure and arrival times for both the soccer game and the coding class. This option would require planning and coordination to ensure he arrives at the game on time and can pick up his daughter afterward.
Using his personal car gives Patrick the freedom to leave at a time that accommodates both the soccer game and the coding class. He can drop off his daughter at her coding class, attend the soccer game, and then pick her up afterward without being restricted by train schedules.
Considering the circumstances, Patrick might find it more convenient to use his personal car to manage both tasks effectively and ensure he can attend his son's soccer game while also ensuring his daughter arrives at her coding class on time.
To learn more about transportation
https://brainly.com/question/32750280
#SPJ11
work out shaded area

Answers
Answer:
A = (1/2)(12)(9 + 14) = 6(23) = 138 m^2
Answer:
Area = 138 m²
Step-by-step explanation:
In the question, we are given a trapezium and told to find its area.
To do so, we must use the formula:
\(\boxed{\mathrm{A = \frac{1}{2} \times (a + b) \times h}}\) ,
where:
A ⇒ area of the trapezium
a, b ⇒ lengths of the parallel sides
h ⇒ perpendicular distance between the two parallel sides
In the given diagram, we can see that the two parallel sides have lengths of 9 m and 14 m. We can also see that the perpendicular distance between them is 12 m.
Therefore, using the formula above, we get:
A = \(\frac{1}{2}\) × (a + b) × h
⇒ A = \(\frac{1}{2}\) × (14 + 9) × 12
⇒ A = \(\frac{1}{2}\) × 23 × 12
⇒ A = 138 m²
Therefore, the area of the given trapezium is 138 m².
6. What is the slope of the line below? *
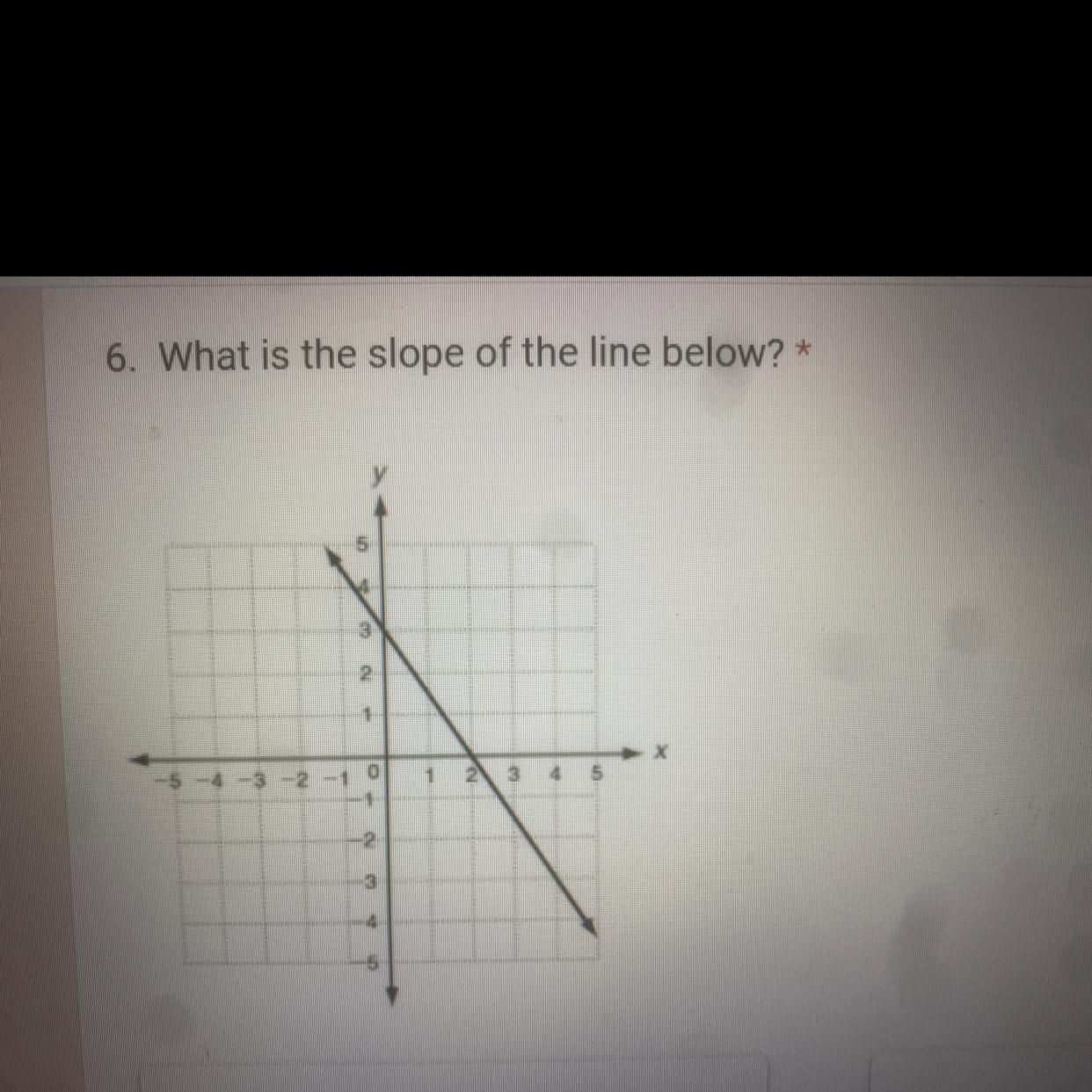
Answers
Answer:3/2
Step-by-step explanation: slope=rise/run=3/2
Please help! 30 points!
Use the numbers:
6 3 5 4 2 1
in that order to make 100. Use brackets and the four operations.
Answers
Answer:
((6 x 3 + 4/2) x 5 ) / 1
The table below shows the results of a survey about vacation destinations and the length of those vacations.
Which of the following includes the correct relative frequency and conclusion based on the table?
A
The relative frequency for traveling in state for longer than a week is 17%. This could be low because people want to spend more time if they have traveled farther.
B
The relative frequency for traveling out of state for longer than a week is 48%. This could be high because people want to spend more time if they have traveled farther.
C
The relative frequency for traveling in state for longer than a week is 30%. This could be low because people want to spend more time if they have traveled farther.
D
The relative frequency for traveling out of state for longer than a week is 83%. This could be high because people want to spend more time if they have traveled farther.

Answers
The correct relative frequency and the conclusion based on the table is B. The relative frequency for traveling out of state for longer than a week is 48%. This could be high because people want to spend more time if they have traveled farther.
Given a table.
Relative frequency of a data set is defined as the ratio of the number of outcomes that occured by the total number of trials.
Total number of surveys = 100
Relative frequency for traveling in state for longer than a week is,
10/100 = 10%
Relative frequency for traveling out of state for longer than a week is,
48/100 = 48%
This must be true since people will be more likely to spend more time if they travelled farther.
Hence the correct option is B.
Learn more about Relative frequency here :
https://brainly.com/question/30466267
#SPJ1
The Arnold Inn offers two plans for wedding parties. Under plan A, the inn charges $30 for each person in attendance. Under plan B, the inn charges $1300 plus $20 for each person in excess of the first 25 who attend. For what size parties will plan B cost less? I do not understand how for Plan b: 1300+20(p-25). I do not understand the part p-25
Answers
ANSWER
81 people
EXPLANATION
Let p be the number of people that attend the party.
Under plan A, the inn charges $30 for each person, so the value y of a party for p people is,
\(y_A=30x\)Then, under plan B, the cost is $1300 for a maximum of 25 people - this means that if 1 to 25 people attend the party, the cost is the same, $1300. For each person in excess of the first 25 - this means for 26, 27, 28, etc, the inn charges $20 each. The cost for plan B is,
\(y_B=1300+20(p-25)\)The last part, (p - 25), is the part of the equation that separates the first 25 attendees. This equation works for 25 people or more, but it is okay to solve this problem. Note that for p = 25, the cost for plan A is,
\(y_A=30\cdot25=750\)Which is less than the cost of plan B ($1300).
We have to find for what number of people attending the party, the cost of plan B is less than the cost of plan A,
\(y_BThis is,\(1300+20(p-25)<30p\)We have to solve this for p. First, apply the distributive property of multiplication over addition/subtract4ion to the 20,
\(\begin{gathered} 1300+20p-20\cdot25<30p \\ 1300+20p-500<30p \end{gathered}\)Add like terms,
\(\begin{gathered} (1300-500)+20p<30p \\ 800+20p<30p \end{gathered}\)Now, subtract 20p from both sides,
\(\begin{gathered} 800+20p-20p<30p-20p \\ 800<10p \end{gathered}\)And divide both sides by 10,
\(\begin{gathered} \frac{800}{10}<\frac{10p}{10} \\ 80For 80 people, the costs of the plans are,
\(\begin{gathered} y_A=30\cdot80=2400 \\ y_B=1300+20(80-25)=1300+20\cdot55=1300+1100=2400 \end{gathered}\)Both have the same cost. The solution to the inequation was the number of people, p, is more than 80. This means that for 81 people the cost of plan B should be less than the cost of plan A,
\(\begin{gathered} y_A=30\cdot81=2430 \\ y_B=1300+20(81-25)=2420 \end{gathered}\)For 81 people, plan B costs $10 less than plan A.
what do parallel line prove
Answers
Answer:
the pairs of corresponding angles are congruent
Step-by-step explanation:
the president of a university claimed that the entering class this year appeared to be larger than the entering class from previous years but their mean sat score is lower than previous years. he took a sample of 30 of this year's entering students and found that their mean sat score is 1,501 with a standard deviation of 53. the university's record indicates that the mean sat score for entering students from previous years is $1,520. he wants to find out if his claim is supported by the evidence at a 5% significance level. which of the following best describes a type i error? the president concludes that the mean sat score of the entering students is lower than previous years when it is indeed not lower the president concludes that the mean sat score of the entering students is higher than previous years when it is indeed higher the president concludes that the mean sat score of the entering students is not lower than previous years when it is indeed lower the president concludes that the mean sat score of the entering students is lower than previous years when it is indeed lower
Answers
The result is not statistically significant.
To test the hypothesis is the mean SAT score is less than 1520 at 5% significance level.
The null hypothesis is
H₀ : μ ≥ 1520
The alternative hypothesis is
Hₐ : μ ≤ 1520
then the test statistic is,
t = (x - μ)/(s/√n)
= (1501 - 1520)/(53/√20)
t = - 1.603
The t-test statistic is - 1.603.
Degree of freedom n - 1 = 20 - 1 = 19
Hence the t-critical value is -1.792.
The conclusion is that the t value corresponds to sample statistics is not fall in the critical region, so the null hypothesis is not rejected at 5% level of significance. There is insignificance evidence indicates that the mean SAT score is less than 1520.
The result is not statistically significant.
To know more about mean score here
https://brainly.com/question/16907497
#SPJ4
8 ft A triangle has an area of 42 cm². The heigh of the triangle is 14 centimeters. What is the length of the base of the triangle?
Answers
Answer:
the length of the base of the triangle is 6 centimeters.
Step-by-step explanation:
We can use the formula for the area of a triangle:
Area = (1/2) x base x height
Substituting the given values:
42 cm² = (1/2) x base x 14 cm
Multiplying both sides by 2:
84 cm² = base x 14 cm
Dividing both sides by 14 cm:
base = 6 cm
know more about area of triangle: brainly.com/question/27683633
#SPJ11
Use the Divergence Theorem to compute the net outward flux of the field F=<-x, 3y, 2z> across the surface S, where S is the boundary of the tetrahedron in the first octant formed by the plane x+y+z=1
Answers
The net outward flux across the boundary of the tetrahedron is: 5, using the concept of gradient of function.
What is the gradient of a function in a vector field?The gradient of a function is related to a vector field and it is derived by using the vector operator ∇ to the scalar function f(x, y, z).
Given vector field:
F = ( -x, 3y, 2 z )
Δ . F = (i δ/δx + j δ/δy + k δ/δz) (-x, 3y, 2 z )
Δ . F = [δ/δx(-x)] + δ/δy (3y) + δ/δz (2z)]
Δ . F = - 1 + 3 + 2
Δ . F = 4
According to divergence theorem;
Flux = ∫∫∫ Δ . (F) dv
x+y+z = 1; so, 1st octant
x from 0 to 1y from 0 to 1 -xz from 0 to 1-x-y∫₀¹∫₀¹⁻ˣ∫₀¹⁻ˣ⁻y (4) dz dy dx
= 4 ∫₀¹∫₀¹⁻ˣ (1 - x - y) dy dx
= 5
Therefore, we can conclude that the net outward flux across the boundary of the tetrahedron is: 5
To learn more about the gradient of a function refer to:
brainly.com/question/6158243
#SPJ4
Which graph shows this system of equations?

Answers
Answer:
third graph
Step-by-step explanation:
the equation of a line in slope- intercept form is
y = mx + c ( m is the slope and c the y- intercept )
y = \(\frac{1}{3}\) x + 12 ← is in slope- intercept form
with slope m = \(\frac{1}{3}\) and y- intercept c = 12
y = 3x + 4 ← is in slope- intercept form
with slope m = 3 and y- intercept c = 4
• If m > 0 , then graph slopes upwards from left to right
Both equations have a positive slope, thus both slope upwards from left to right.
the first equation has a y- intercept of 12
the second equation has a y- intercept of 4
Theses lines are represented in the third graph
5. define unbiased estimator. why are unbiased estimators useful? (2 points)
Answers
An estimator is said to be unbiased if the expected value of the estimator is equal to the true value of the parameter being estimated.
Unbiased estimators are useful because they provide an estimate that, on average, is equal to the true value of the parameter, making them desirable for making accurate inferences about a population.
In statistics, an estimator is a statistic used to estimate the value of an unknown parameter in a population. An estimator is said to be unbiased if, on average, it produces an estimate that is equal to the true value of the parameter. An unbiased estimator is desirable because it provides an estimate that is, on average, accurate, which is important for making inferences about a population.
Biased estimators, on the other hand, tend to consistently overestimate or underestimate the true value of the parameter, which can lead to incorrect conclusions. Therefore, unbiased estimators are useful because they provide more accurate estimates, which can lead to more reliable inferences about a population.
You can learn more about Unbiased estimators at
https://brainly.com/question/29646467
#SPJ11
4. Show that f(x,y)=x^2y is homogeneous, and find its degree of homogeneity. 5. Which of the following functions f(x,y) are homothetic? Explain. (a) f(x,y)=(xy)^2+1 (b) f(x,y)=x^2+y^3 3
Answers
4. f(x,y) is homogeneous of degree 2.
5. a) f(x,y) is homothetic with h(x,y) = xy and g(x) = x-1
4. Show that f(x,y)=\(x^2\)y is homogeneous, and find its degree of homogeneity:
A function is said to be homogeneous of degree k, if it satisfies the condition:
f(tx,ty) = \(t^k\)f(x,y)
We have f(x,y) = \(x^2\)y. Let’s check if it satisfies the above condition:
f(tx,ty) = \((tx)^2(ty) = t^3x^2y = t^2(x^2y\)) = \(t^2\)f(x,y)
Hence f(x,y) is homogeneous of degree 2.
5. Which of the following functions f(x,y) are homothetic? Explain.
(a) f(x,y)=\((xy)^2\)+1
(b) f(x,y)=\(x^2+y^3\)
Let us first understand the meaning of homothetic transformation.
A homothetic transformation is a non-rigid transformation of the Euclidean plane that preserves the direction of the straight lines but not their length. It stretches or shrinks the plane by a constant factor called the dilation.
Let’s now find out whether the given functions are homothetic or not.
(a) f(x,y)=\((xy)^2\)+1
In order to check if f(x,y) is homothetic or not, we need to check if the function satisfies the following condition:
f(x,y) = g(h(x,y))
where g is a strictly monotonic function and h is a homogeneous function with degree 1
We have
f(x,y) = \((xy)^2\)+1
Let’s assume g(x) = x - 1, then g(x+1) = x
Similarly, let’s assume h(x,y) = (xy), then h(tx,ty) = \(t^2\)h(x,y)
Now, we have
g(h(x,y)) = h(x,y) - 1 = (xy) - 1
Thus f(x,y) is homothetic with h(x,y) = xy and g(x) = x-1
(b) f(x,y)=\(x^2+y^3\)
We can’t write this function in the form f(x,y) = g(h(x,y)) where h(x,y) is a homogeneous function with degree 1. Hence this function is not homothetic.
To leran more about degree of homogeneity, refer:-
https://brainly.com/question/15395117
#SPJ11
A wheel has a diameter of 40 cm, to the nearest 10 cm.
Write an inequality to show
a the lower and upper bounds for the diameter d of the wheel
b the lower and upper bounds for the circumference C of the wheel.

Answers
a) The diameter d of the wheel has bounds:
35 cm ≤ d ≤ 45 cm
b) The circumference C has bounds, using C = πd:
π * 35 cm ≤ C ≤ π * 45 cm
How to solveThe inequality representing the lower and upper bounds for the diameter d is:
35 cm ≤ d ≤ 45 cm
b) For the lower bound, we substitute the lower bound of the diameter (35 cm) into the formula:
\(C_l_o_w_e_r\) = π * 35 cm
For the upper bound, we substitute the upper bound of the diameter (45 cm) into the formula:
\(C_u_p_p_e_r\) = π * 45 cm
The inequality representing the lower and upper bounds for the circumference C is:
π * 35 cm ≤ C ≤ π * 45 cm
Read more about inequality here:
https://brainly.com/question/24372553
#SPJ1
Zero is less than negative fifteen decreased by y, solve for y.
av <15
what is the answer?
Answers
The inequality equation will be 0 < -15 - y. Then the value of the variable y is less than negative 15.
What is inequality?Inequality is defined as an equation that does not contain an equal sign. Inequality is a term that describes a statement's relative size and can be used to compare these two claims.
Zero is less than negative fifteen decreased by y, can be written as mathematically
0 < -15 - y
Then solving for y, we have
y < -15
The value of the variable y is less than negative 15.
More about the inequality link is given below.
https://brainly.com/question/19491153
#SPJ1