what are all the place values ?
Answers
Answer:
ones, tens,hundreds,ten thousands, hundred thousands,million, tillion
Step-by-step explanation:
ones,tens,hundreds,
Related Questions
5-time x, increased by 2
Answers
Answer:
i think it would be 27
Step-by-step explanation
1: 7
2: 12
3: 17
4:22
5:27
6:32
7:37
8: 42
9:47
10:52
the increase for each number will be 5
or if u want the increase to be 2 you can go :
1: 5
2: 9
3: 13 ect.
you get the point:)
i hope this helpsss:)))
brainliest pleasee<33
have and amazing day
Can someone please help me with this quick

Answers
Answer:
Minimum = -1
Maximum = 3
Step-by-step explanation:
∛-10+9 = ∛-1 = -1
∛18+9 = ∛27 = 3
How many classrooms would be necessary to hold 1,000,000 inflated balloons? (Assume one balloon is about 1 ft3 and a typical classroom is about 35 ft × 50 ft × 15 ft. Round your answer to the nearest number of classrooms.)
Answers
One balloon = 1 cube ft. Using this value and multiplying it by 1,000,000, we can find how much space all of these would take up. Since 1 times anything is just the unchanged value,
• a million inflated balloons = 1000000 ft^3.
The classroom has dimensions 35, 50, and 15 ft. We can use these values to find the classroom’s volume. The equation for Volume of a rectangular prism: V = lwh, where l is length, w is width, and h is height. Substitute given dimensions into this equation:
• V = 35*50*15 = 26250 ft^3.
now, what times 26250 will equal 1000000? Well, let’s set up an equation and solve for x, the number of classrooms.
• 26,250x = 1,000,000. Divide both sides by 26250 to get x alone:
• x = 38.0952.
Approximately 38 classrooms are necessary to hold 1,000,000 inflated balloons.
Check: when x is 38: 26,250(38) = 997,500 ft^3. When x is 39: 26,250(38) = 1,023,750 ft^3. x = 38 is more accurate.
**(I will note, however, that I’m not sure if you’re instructed to round according to the decimal rules or round UP a whole number because that extra .0952 needs to be included).
To hold 1,000,000 inflated balloons,
38 classrooms are needed.
What is volume?In three-dimensional space,
the amount of space taken by an object is the volume of that object.
The volume of the cubic,
= length x width x height
Given:
The dimensions of the normal classroom are 15 ft × 50 ft × 35 ft.
The volume of the classroom,
= 15 ft by 50 ft by 35 ft.
= 26250 cubic feet.
The number of classrooms,
= 1,000,000 / 26250
Simplifying the fraction,
we get,
= 38.09
≈ 38 to the nearest whole number.
Therefore, 38 classrooms are required.
To learn more about the volume;
https://brainly.com/question/23477586
#SPJ2
Solve the right triangle below. Round all your answers to the nearest tenth. Measure of angle X = ______

Answers
Remember the Pythagorean theorem. A^2+ B^2= C^2. The hypotenuse, or 9 (in this question) will always be C
Which of the following sets are equal to each other: Ø, {Ø}, {Ø}?
Answers
Answer:
{Ø}, {Ø} - these two
Dana is making bean soup. The recipe she has makes 10 servings and uses
3/4
of a pound of beans. How many total pounds of beans does she need to make 5 servings of soup?
She has
1/16
of a pound of beans in one container and
1/4
of a pound of beans in another container. How many more pounds of beans does Dana need to make the 5 servings of soup? Show your work or explain your answer.
Answers
Solve for X
4(x + 3) = 2(x - 1)
Answers
4x+12=2x-2
2. Take one side away from the other
4x-2x =2x
2x+12=-2
-12
2x=-14
/2
X=-7
Anita, Byron, Carlos, and Dominique buy a gift for their grandmother. They split the cost equally and each pay $14.62. Which equation represents d, the cost of the gift in dollars? 14.62 = d minus 4 14.62 = d divided by 4 14.62 minus 4 = d 14.62 divided by 4 = d
Answers
Answer:
Answer is D
Step-by-step explanation:
$14.62(4) = D
Answer:
b is the answer because there is 4 people and d devided by 4 = 14.62
Step-by-step explanation:
Kate has a negative bank account balance of $100. If she is depositing $5 a day , how long until she has a negative balance of only $30?

Answers
Answer:
14 days
Step-by-step explanation:
-100 +5+5+5+5+5+5+5+5+5+5+5+5+5+5= -30
Simplify.
3y - 4x + 6x - y
The simplified expression is???
Answers
Answer:
2y-4x+6x
=2y+2x
Step-by-step explanation:
Answer:
2x+2y
Step-by-step explanation:
Let's simplify step-by-step.
3y−4x+6x−y
=3y+−4x+6x+−y
Combine Like Terms:
=3y+−4x+6x+−y
=(−4x+6x)+(3y+−y)
=2x+2y
-6+x/x^4 limit at x →0
Answers
Answer:
not existing
Step-by-step explanation:
\( \frac{ - 6 + x}{ {x}^{4} } \)
lim x goes to 0 is
\( \frac{ - 6 + 0}{ {0}^{4} } = \frac{ - 6}{0} \)
so not exist
I'm not sure if u mean that or this

an airplane takes 3 hours to travel a distance of 1440 miles with the wind. The return trip takes 4 hours against the wind. Find the speed of the plane in the still air and the speed of the wind.
Answers
Answer:
The speed of the plane in the still air is 420 miles/hour
The speed of the wind 60 miles/hour
Step-by-step explanation:
Let the speed of the plane with the wind be v
Let the speed of the plane against the wind be u
Now, speed = distance/time
With the wind,
v = (1440 miles)/(3 hours) = 480 miles/hour
v = 480 miles/hour
Against the wind,
u = (1440 miles)/(4 hours) = 360 miles/hour
u = 360 miles/hour
Now, let the speed of plane be p, and speed of wind be w,
Now, with the wind, the speed is 480 mph,
so,
speed of plane + speed of wind = 480 mph
p + w = 480 (i)
and against the wind, the speed is 360 mph,
so,
speed of plane - speed of wind = 360mph
p-w = 360 (ii)
adding equations (i) and (ii), we get,
p+w + p-w = 480 + 360
2p = 840
p = 840/2
p = 420 miles/hour
Then, the speed of the wind will be,
p + w = 480,
420 + w = 480
w = 480 - 420
w = 60 miles/hour
The speed of the plane in still air is calculated to be 420 mph, and the speed of the wind is calculated to be 60 mph by solving the two simultaneous equations obtained from the time, rate, and distance relationship.
Explanation:This problem is about the rate, time, and distance relationships. The rate at which the airplane travels in still air is r (unaffected by wind), and the speed of the wind is w. When the plane flies with the wind, it is 'assisted' and therefore travels faster - at a speed of (r + w); against the wind, it travels slower - at a speed of (r - w).
From the problem, we know that:
The trip with the wind covers 1440 miles in 3 hours, so (r + w) * 3 = 1440The return trip against the wind covers the same 1440 miles in 4 hours, so (r - w) * 4 = 1440By solving these two equations, we get the following:
r + w = 480r - w = 360Adding these two gives 2r = 840 => r = 420 mph (the speed of the plane in still air), and subtracting gives 2w = 120 => w = 60 mph (the speed of the wind).
Learn more about Simultaneous Equations here:https://brainly.com/question/31913520
#SPJ2
a triangle has angles measuring 45°, 55°, and 80°. it is dilated by a scale factor of 2. what are the angle measures, in order from least to greatest, of the dilated image? enter the correct answers in the boxes.
Answers
Answer:
\(45\)°, \(55\)°, and \(80\)°
Step-by-step explanation:
Dilations preserve angle measures, regardless of the scale factor. Therefore, the angle measures of the image will be the same of that of the pre-image, so our answer is still \(45\)°, \(55\)°, and \(80\)°. Hope this helps!
solve the PDE using separation of variables method Uxx = 1/2 Ut 0< X <3 with U(0,t) = U(3, t)=0, U(0, t) = 5sin(4πx)
Answers
The general solution of the partial differential equation is:
U(x, t) = Σ [Aₙ*sin((nπ/3)x)]*e^(-(nπ/3)²t)
How to solve Partial Differential Equations?The partial differential equation (PDE) is given as:
Uxx = (1/2)Ut with the boundary and initial conditions as 0< X <3 with U(0,t) = U(3, t)=0, U(0, t) = 5sin(4πx)
Assume that the solution can be written as a product of two functions:
U(x, t) = X(x)T(t)
Substituting this into the PDE, we have:
X''(x)T(t) = (1/2)X(x)T'(t)
Dividing both sides by X(x)T(t), we get:
(X''(x))/X(x) = (1/2)(T'(t))/T(t)
Since the left side only depends on x and the right side only depends on t, both sides must be equal to a constant, denoted as -λ²:
(X''(x))/X(x) = -λ²
(1/2)(T'(t))/T(t) = -λ²
Simplifying the second equation, we have:
T'(t)/T(t) = -2λ²
Solving the second equation, we find:
T(t) = Ce^(-2λ²t)
Applying the boundary condition U(0, t) = 0, we have:
U(0, t) = X(0)T(t) = 0
Since T(t) ≠ 0, we must have X(0) = 0.
Applying the boundary condition U(3, t) = 0, we have:
U(3, t) = X(3)T(t) = 0
Again, since T(t) ≠ 0, we must have X(3) = 0.
Therefore, we can conclude that X(x) must satisfy the following boundary value problem:
X''(x)/X(x) = -λ²
X(0) = 0
X(3) = 0
The general solution to this ordinary differential equation is given by:
X(x) = Asin(λx) + Bcos(λx)
Applying the initial condition U(x, 0) = 5*sin(4πx), we have:
U(x, 0) = X(x)T(0) = X(x)C
Comparing this with the given initial condition, we can conclude that T(0) = C = 5.
Therefore, the complete solution for U(x, t) is given by:
U(x, t) = Σ [Aₙsin(λₙx) + Bₙcos(λₙx)]*e^(-2(λₙ)²t)
where:
Σ represents the summation over all values of n
λₙ are the eigenvalues obtained from solving the boundary value problem for X(x).
To find the eigenvalues λₙ, we substitute the boundary conditions into the general solution for X(x):
X(0) = 0: Aₙsin(0) + Bₙcos(0) = 0
X(3) = 0: Aₙsin(3λₙ) + Bₙcos(3λₙ) = 0
From the first equation, we have Bₙ = 0.
From the second equation, we have Aₙ*sin(3λₙ) = 0. Since Aₙ ≠ 0, we must have sin(3λₙ) = 0.
This implies that 3λₙ = nπ, where n is an integer.
Therefore, λₙ = (nπ)/3.
Substituting the eigenvalues into the general solution, we have:
U(x, t) = Σ [Aₙ*sin((nπ/3)x)]*e^(-(nπ/3)²t)
where Aₙ are the coefficients that can be determined from the initial condition.
Read more about Partial Differential Equations at: https://brainly.com/question/28099315
#SPJ1
On Friday, three friends shared how much they read during the week
Barbara read the first 100 pages from a 320-page in the last 4 days
Judy read the first 54 pages from a 260-page book in the last 3 days.
Nancy read the first 160 pages from a 480-page book in the last 5 days
Order the friends from the first one who is predicted to finish her book to the third one who is predicted to finish her book(Show all work)
Answers
The friends from the first one who is predicted to finish her book to the third one who is predicted to finish her book is given by the order Nancy > Barbara > Judy
Given data ,
The total number of pages in each friend's book as follows:
Barbara's book: 320 pages
Judy's book: 260 pages
Nancy's book: 480 pages
Now, we can calculate their reading rates as pages read per day:
Barbara's reading rate: 100 pages / 4 days = 25 pages/day
Judy's reading rate: 54 pages / 3 days = 18 pages/day
Nancy's reading rate: 160 pages / 5 days = 32 pages/day
Hence , the descending order is Nancy > Barbara > Judy
To learn more about descending order click :
https://brainly.com/question/13174148
#SPJ1
A random sample of 4 homes for sale in NW Gainesville between 16000 and 20000 square feet had a mean of $156100 and a standard deviation of $13660. Construct a 95% confidence interval for the average home of this size.
Answers
Answer:
142713.2≤x≤169486.8
Step-by-step explanation:
Confidence interval is expressed according to the equation
CI = xbar± z•s/√n
xbar is the mean = $15610
z is the z-score at 95% CI = 1.96
s is the standard deviation = 13660
n is the sample size= 4
Substitute into the formula
CI = 156100±(1.96×13660/√4)
CI = 156100±(1.96×13660/2)
CI = 156100±(1.96×6830)
CI = 156100±(13386.8)
CI = (156100-13386.8, 156100-13386.8)
CI = (142,713.2, 169,486.8)
Hence the 95% confidence interval for the average home of this size is 142713.2≤x≤169486.8
Using the t-distribution, it is found that the 95% confidence interval for the average price of a home of this size is ($134,364, $177,836).
In this problem, we have the standard deviation for the sample, thus, the t-distribution is used.
The sample mean is \(\overline{x} = 156100\).The sample standard deviation is \(s = 13660\).Sample of 4 homes, thus \(n = 4\).The first step is finding the number of degrees of freedom, which is the sample size subtracted by 1, thus \(df = 4 - 1 = 3\).
Then, we find the critical value for a 95% confidence interval with 3 df, which looking at a t-table or using a calculator is given by t = 3.1824.
The margin of error is:
\(M = t\frac{s}{\sqrt{n}}\)
Thus:
\(M = 3.1824\frac{13660}{\sqrt{4}} = 21736\)
The confidence interval is:
\(\overline{x} \pm M\)
Then
\(\overline{x} - M = 156100 - 21736 = 134364\)
\(\overline{x} + M = 156100 + 21736 = 177836\)
The 95% confidence interval is ($134,364, $177,836).
A similar problem is given at https://brainly.com/question/15180581
What are the number whose absolute value is -8
Answers
Well, the only absolute value of -8 is 8.
Answer:
8
Step-by-step explanation:
Any absolute value of a negative, is the same number but in positive form.
Ex : I-6I = +6
Which of the following scenarios would generate outcomes and probabilities that are equivalent to identifying the sex of 3 successive children? flipping a fair coin 2
times flipping a fair coin 3 times
rolling a fair die 2 times
rolling a fair die 3 times
Answers
Answer: Flipping a coin 3 times
Step-by-step explanation:
Answer:
flipping a fair coin three times
Step-by-step explanation:
edg 2020-2021
How would you describe the relationship between the real zeros and x-intercepts of the function.
Answers
Answer:
real zeros and fake zerps
Step-by-step explanation:
1. ALUMMUNI PLC. Produces three models of tractors: Metakeb, Mewesson, Metekem Each unit of Metakeb, Mewesson and Metekem requires the following amounts of time in minumtes in each of the indicated departments.
Machining dep't
Inspection dep't
(in minutes)
(in minutes)
(in minutes)
Metakeb
1200
2400
600
Mewesson
1800
1200
3000
Metekem
3000
Assembly dep't
2400
1200
Suppose the total time available per month in machining, assembly and inspection departments are 1050, 1160 and 830 hours respectively.
Required:
Determine the number of units of each product to be produced in a month to use up all the available resources (use Gaussaian method)
Answers
The company should produce 235 units of Metakeb, 96 units of Mewesson, and 17 units of Metekem per month to use up all the available resources.
What is the Gaussian method?
The Gaussian method, also known as Gaussian elimination or row reduction, is a technique for solving systems of linear equations. It involves performing a sequence of operations on the rows of a matrix to transform it into an equivalent matrix that is in row echelon form or reduced row echelon form.
To use the Gaussian method, we need to set up a system of linear equations based on the given information. Let x, y, and z be the number of units of Metakeb, Mewesson, and Metekem produced per month, respectively. Then we have:
Machining department: 1200x + 1800y + 3000z = 1050(60)
Inspection department: 2400x + 1200y = 1160(60)
Assembly department: 600x + 3000y = 830(60)
Simplifying these equations, we get:
Machining department: 20x + 30y + 50z = 3150
Inspection department: 8x + 4y = 232
Assembly department: x + 5y = 139
Now we can use the Gaussian method to solve for x, y, and z:
Step 1: Write the augmented matrix:
| 20 30 50 | 3150 |
| 8 4 0 | 232 |
| 1 5 0 | 139 |
Step 2: Use row operations to get the matrix in row echelon form:
R2 → R2 - 4/5 R3
R1 → R1 - 20R3
| 0 -2 50 | 850 |
| 0 2 -4 | -28 |
| 1 5 0 | 139 |
R2→ -1/2 R2
R1 → R1 + R2
| 0 1 -25 | 407 |
| 0 1 -2 | 14 |
| 1 5 0 | 139 |
R1→ R1 - R2
| 0 0 -23 | 393 |
| 0 1 -2 | 14 |
| 1 5 0 | 139 |
R3→ R3 - 5R2
| 0 0 -23 | 393 |
| 0 1 -2 | 14 |
| 1 0 10 | 65 |
R1→ -1/23 R1
| 0 0 1 | -17 |
| 0 1 -2 | 14 |
| 1 0 10 | 65 |
R2 → R2 + 2R3
| 0 0 1 | -17 |
| 0 1 0 | 96 |
| 1 0 10 | 65 |
R3 → R3 - 10R1
| 0 0 1 | -17 |
| 0 1 0 | 96 |
| 1 0 0 | 235 |
Step 3: Read off the solution from the row echelon form:
z = -17
y = 96
x = 235
Therefore, the company should produce 235 units of Metakeb, 96 units of Mewesson, and 17 units of Metekem per month to use up all the available resources.
To know more about the gaussian method visit:
brainly.com/question/28537650
#SPJ1
Question 4 of 10
What is i86
O A. -1
B. 1
O c. i
O D. 1
Answers
Answer:
option c-i is the answer
The product of two negative integers is a negative integer.
Answers
Answer:
False. The product of two negative integers is a positive integer.
Given the two rectangles below. Find the area of the shaded region.

Answers
Answer:
The area of the shaded region is 36.
Step-by-step explanation:
First, let's find the area of the rectangle as a whole, which will be 5*10 = 50. How did we get 50? The right side is 5 (from 2+3), and the top is 10 (3+7). Multiplying those numbers together will give you the area.
Now, the problem asks to find the shaded region. Let's solve for the area of the non-shaded region: (7*2) = 14.
Now, we can subtract the whole rectangle area minus the non-shaded region to find the shaded region:
50 - 14 = 36
19. Suppose the function ƒ(t) = et describes the growth of a colony of bacteria, where t is hours. Find the number of bacteria present at 5 hours.

Answers
Answer:
To get the population of the bacteria at a time t, we just plug in the given value of t
so in this case, we will put 5 in the place of t
f(t) = \(e^{t}\)
f(5) = \(e^{5}\)
we know that the value of e is about 2.7. So the population of the bacteria after 5 hours will be 2.7 to the power 5
which will be equal to:
b) 148.413
note: using 2.7 in the calculation will give slightly different answer since it is an estimated value, i suggest using 'e' in the actual calculation
Identify whether each function is linear or exponential.
Function A:
Function C
Function D:
You have $200 in
a savings
account that
earns 1% annual
interest
b. Which function has the greatest growth factor? Justify your response.

Answers
Answer:
A)
Function A: Exponential
Function B: Linear
Function C: Exponential
Function D: Exponential
B) Function A
Step-by-step explanation:
Function A: This is exponential because- (1, 3)(2,9)(3,27)
It is not going up by the same number each time. However, it is multiplying by 3 each time which means it is exponential.
Function B: This is linear because- (1, 64)(1, 80)(1, 96)
It is going up by 16 each time, (a constant number) which means it is linear.
Function C: This is exponential because- there is a curve, linear is always a straight line. But, this has a curve which means it is exponential.
Function D: This is exponential because- It is increasing by a percentage and not a constant number. It is increasing by 1% which means it is exponential.
The function that has the greatest growth factor is Function A because, Function A multiplies by 3 each time. Function B is linear, exponential functions always pass linear functions despite how "steep" they are. Eventually, the exponential function will surpass it. Function C is also exponential but is not as "steep" as Function A. Function A multiplies by 3 each time but Function C increases less. Function D is also exponential, and for the same reasons as Function C, Function A has the greatest growth factor.
Anthony surveys a group of students at his school about whether they play a
sport. This table shows the results broken down by gender.
Boys
Girls
Total
Play a sport
95
76
171
Do not play a
sport
45
59
104
A. Yes, they are independent, because P(girl)
a sport) ~0.62
Are being a girl and playing a sport independent events? Why or why not?
B. Yes, they are independent, because P(girl)
a sport) -0.44
Total
C. No, they are not independent, because P(girl) 0.49 and
P(girl plays a sport) ~ 0.62.
140
135
275
0.49 and Pigirl | plays
0.49 and P(girl plays
D. No, they are not independent, because P(girl)-0.49 and
Pigirl plays a sport)~0.44.
Answers
Being a girl and playing a sport are C. No, they are not independent events, because P(girl) 0.49 and P(girl plays a sport) ~ 0.62.
Let's consider the probabilities:
P(girl) = (number of girls) / (total number of students) = 135 / 275 ≈ 0.49
P(girl plays a sport) = (number of girls playing a sport) / (total number of students) = 76 / 275 ≈ 0.276
If being a girl and playing a sport were independent events, the joint probability would be the product of the individual probabilities:
P(girl) × P(girl plays a sport) ≈ 0.49 × 0.276 ≈ 0.13524
However, the actual joint probability is different from the expected value:
P(girl, plays a sport) ≈ 76 / 275 ≈ 0.276
Since the joint probability does not match the product of the individual probabilities, we can conclude that being a girl and playing a sport are not independent events based on the given data.
Therefore, option C. No, they are not independent, because P(girl) 0.49 and P(girl plays a sport) ~ 0.62. is the correct answer.
For more questions on events
https://brainly.com/question/29782219
#SPJ8
3 3/4 ÷ 5 5/8
write in simplest form. Check by multiplying.
pls teach me how to answer it. I'll give brainliesnt if correct.
Answers
Step-by-step explanation:
3¾ divided by 5⅝4*3+3 = 15/4
8*5+5 = 45/8
15/4 * 8/45 =
2/3
Solve the quadratic equation by factoring 9x^2 -16 = 0
Answers
Answer: x= - 4/3 and x = 4/3
Step-by-step explanation:
(3x-4) times (3x+4) = 0
The function f(x) = -2(4)²+1 +140 represents the number of tokens a child has x hours after arriving at an arcade.
What is the practical domain and range of the function?
Enter your answer by filling in the boxes to correctly complete the statements. If necessary, round to the nearest hundredth.
The practical domain of the situation is ?
The practical range of the situation is ?
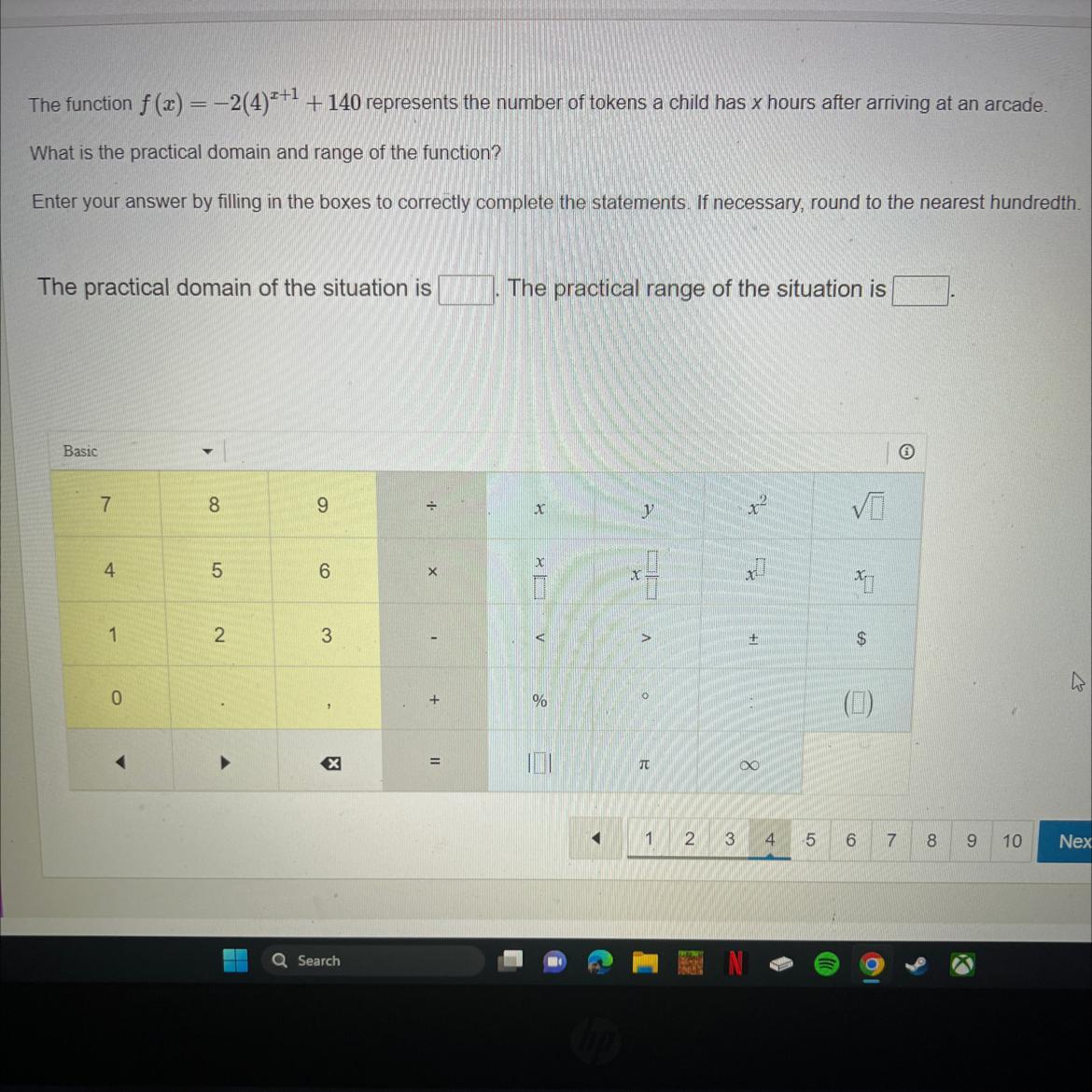
Answers
The practical domain of the situation is all real numbers, since there is no restriction on the number of hours the child can spend at the arcade.
The practical range of the situation is [1,140], since the minimum value of the function is 1 and the maximum value is 140.
help me about this integral

Answers
The gradient theorem applies here, because we can find a scalar function f for which ∇ f (or the gradient of f ) is equal to the underlying vector field:
\(\nabla f(x,y,z)=\langle2xy,x^2-z^2,-2yz\rangle\)
We have
\(\dfrac{\partial f}{\partial x}=2xy\implies f(x,y,z)=x^2y+g(y,z)\)
\(\dfrac{\partial f}{\partial y}=x^2-z^2=x^2+\dfrac{\partial g}{\partial y}\implies\dfrac{\partial g}{\partial y}=-z^2\implies g(y,z)=-yz^2+h(z)\)
\(\dfrac{\partial f}{\partial z}=-2yz=-2yz+\dfrac{\mathrm dh}{\mathrm dz}\implies\dfrac{\mathrm dh}{\mathrm dz}=0\implies h(z)=C\)
where C is an arbitrary constant.
So we found
\(f(x,y,z)=x^2y-yz^2+C\)
and by the gradient theorem,
\(\displaystyle\int_{(0,0,0)}^{(1,2,3)}\nabla f\cdot\langle\mathrm dx,\mathrm dy,\mathrm dz\rangle=f(1,2,3)-f(0,0,0)=\boxed{-16}\)