What fraction of the floats were not from a sports team? Write in simplest form.

Answers
Answer:
\(\frac{2}{3}\)
Step-by-step explanation:
Fraction of the floats that belongs to sports team = \(\frac{6}{18}\)
= \(\frac{1}{3}\)
Therefore, fraction of floats that were not from a sports team = 1 - fraction of floats that belongs to sports team
= 1 - \(\frac{1}{3}\)
= \(\frac{2}{3}\)
\(\frac{2}{3}\)rd fraction of Parade Float were not from a sports team.
Related Questions
The function f(x) is shown in this graph.
(0,2)
The function g(x) = -5x - 6. Compare the slopes.
A. The slope of f(x) is the same as the slope of g(x).
B. The slope of f(x) is undefined, and the slope of g(x) is negative.C. The slope of f(x) is greater than the slope of g(x).D. The slope of f(x) is less than the slope of g(x).

Answers
Answer:
D. The slope of f(x) is less than the slope of g(x).
Step-by-step explanation:
✔️Slope of f(x):
Using two points on the line, (0, 2) and (1, -1),
Slope (m) = change in y/change in x
Slope (m) = (-1 - 2)/(1 - 0) = -3/1 = -3
Slope of f(x) = -3
✔️Slope of g(x) = -5x - 6:
The slope of g(x) is -5.
Therefore f(x) has a lesser absolute slope value (3) compared to the absolute slope value of g(x) (5).
Thus, D. the slope of f(x) is less than the slope of g(x).
Divide 2.9 x 107 by 6.9 x 103 by using scientific notation. Round your answer to one decimal place in scientific notation with no spaces.
Answers
Step-by-step explanation:
Its answer should be 4.366117912↑-01
Carla asked students at a lunch table what their main course they liked. Out of these students, 28n liked pizza, 15 liked chicken nuggets, and 8 liked both. what is the probability that a randomly selected student will like pizza but not chicken nuggets?
Answers
The probability that a randomly selected student will like pizza but not chicken nuggets is (28n - 8)/(28n + 7), where 28n is the students who like pizza and 8 is students who like both pizza and chicken nuggets.
To find the probability that a randomly selected student will like pizza but not chicken nuggets.
Let P = the number of students who like pizza but not chicken nuggets
Then, P = the number of students who like pizza - the number of students who like both pizza and chicken nuggets
P = 28n - 8
So, the probability that a randomly selected student will like pizza but not chicken nuggets is:
P(Pizza but not nuggets) = P/(Total number of students)
We can find the total number of students who like either pizza or chicken nuggets by adding the number of students who like pizza and the number of students who like chicken nuggets, and then subtracting the number of students who like both:
Total number of students = 28n + 15 - 8 = 28n + 7
So, the probability that a randomly selected student will like pizza but not chicken nuggets is:
P(Pizza but not nuggets) = P/(Total number of students) = (28n - 8)/(28n + 7)
To learn more about probability please click on below link
https://brainly.com/question/16484393
#SPJ1
Jayda is older than her 12-year-old sister. Write an inequality for j, Jayda's age.
Answers
The inequality states that Jayda's age (j) is greater than 12 i.e., j > 12.
Let j represent Jayda's age.
Since Jayda is older than her 12-year-old sister, we can write the inequality:
j > 12
Thus, the inequality states that Jayda's age (j) is greater than 12.
Learn more about Inequality here:
https://brainly.com/question/20383699
#SPJ1
Please answer this correctly

Answers
Answer:
1/7
Step-by-step explanation:
The probability of picking an even number is 3/7.
Without putting the first card back, the probability of picking an even number again is 2/6.
\(3/7 \times 2/6\)
\(= 6/42\)
\(=1/7\)
y=15x+2
-15x+y=1
Is it one solution,no solution or infinite solution? Show work please :)
(50 points!!)
Answers
Answer:
Since slopes are same. and y intercept is different, the system has no solution.
Step-by-step explanation:
When dealing with linear equations, put the equation in slope intercept form,
\(y = mx + b\)
unless not asked to.
Equation 1 is in slope intercept form, but the second one isn't
\( - 15x + y = 1\)
Isolate y.
\(y = 15x + 1\)
So our equations is
\(y = 15x + 1\)
\(y = 15x + 2\)
Notice how the slope is the same and the y intercept is different.
This means s the system will never have a consistent system.
Why? The y intercept gives us the a distinct place for our linear equations.
If two places start in a different place, and have a constant slope, they will never intersect which thus forms a solution.
So the answer is no solution.
Answer:
No solutions.Step-by-step explanation:
Let's organize both equations.
y = 15x + 2 (Organized)-15x + y = 1=> y = 15x + 1 (Organized)We now know that the organized equations are y = 15x + 1 and y = 15x + 2
We can see that their slopes are same. However, it's y-intercepts are different. These equations form parallel lines which basically means that these equations have no solutions. Please check out my graph to learn more.

Which of the following is correct? Multiple Choice When the sample size increases, both α and β may decrease. Type II error can only occur when you reject H0. Type I error can only occur if you fail to reject H0. The level of significance is the probability of Type II error.
Answers
Answer:
(A) When the sample size increases, both α and β may decrease.
Step-by-step explanation:
Which of the following is correct?
(A) This option is right.
When a sample's size increases, the values for alpha and beta may decrease; if and only if sample size is the denominator in the slope equation (in each case) and the numerator stays the same (that is, ceteris paribus; all other things being equal). The larger the denominator, the smaller the slope value for alpha and beta.
(B) This option is wrong
Type 2 error can only occur when you fail to reject a true H0
(C) This option is wrong
Type 1 error can only occur if or when you don't reject a false H0
(D) This option is wrong
The level of significance is the probability of a Type 1 error, not the probability of a Type 2 error.
A professor has learned that nine students in her class of 35 will cheat on the exam. She decides to focus her attention on ten randomly chosen students during the exam. a. What is the probability that she finds at least one of the students cheating
Answers
Answer:
\(\frac{73,331}{75,516}\approx 97.11\%\)
Step-by-step explanation:
The probability that she will find at least one student cheating is equal to the probability that she finds no students cheating subtracted from 1.
Each time she randomly chooses a student the probability she will catch a cheater is equal to the number of cheaters divided by the number of students.
Therefore, for the first student she chooses, there is a \(\frac{9}{35}\) chance that the student chosen is a cheater and therefore a \(\frac{26}{35}\) chance she does not catch a cheater. For the second student, there are only 34 students to choose from. If we stipulate that the first student chosen was not a cheater, then there is a \(\frac{9}{34}\) chance she will catch a cheater and a \(\frac{25}{34}\) chance she does not catch the cheater.
Therefore, the probability she does not catch a single cheater after randomly choosing ten students is equal to:
\(\frac{26}{35}\cdot \frac{25}{34}\cdot \frac{24}{33}\cdot \frac{23}{32}\cdot \frac{22}{31}\cdot \frac{21}{30}\cdot \frac{20}{29}\cdot \frac{19}{28}\cdot \frac{18}{27}\cdot \frac{17}{26}\)
Subtract this from one to get the probability she finds at least one of the students cheating after randomly selecting nine students. Let event A occur when the professor finds at least one student cheating after randomly selecting ten students from a group of 35 students.
\(P(A)=1-\frac{26}{35}\cdot \frac{25}{34}\cdot \frac{24}{33}\cdot \frac{23}{32}\cdot \frac{22}{31}\cdot \frac{21}{30}\cdot \frac{20}{29}\cdot \frac{19}{28}\cdot \frac{18}{27}\cdot \frac{17}{26},\\\\P(A)=1-\frac{2,185}{75,516},\\\\P(A)=\boxed{\frac{73,331}{75,516}}\approx 0.97106573441\approx \boxed{97.11\%}\)
Find the value of z. You must show work to receive full credit.

Answers
The value of z from the cyclic quadrilateral as described is; 173/22.
What is the value of z?Since the quadrilateral TUVW is a cyclic quadrilateral, it follows that the opposite angles of the quadrilateral are supplementary and hence, amount to 180.
On this note, 14z -7 +8z = 360
22z -7 = 180
22z = 180 -7
z = 173/22
Read more on cyclic quadrilateral;
https://brainly.com/question/10057464
#SPJ1
i need help can someone help me

Answers
The value of the side labelled x is equal to 3.8 to the nearest tenth using the trigonometric ratio of sine.
What is trigonometric ratios?The trigonometric ratios is concerned with the relationship of an angle of a right-angled triangle to ratios of two side lengths.
The basic trigonometric ratios includes;
sine, cosine and tangent.
Considering the sine of angle 41°
sin 41° = 2.5/x {opposite/hypotenuse}
x = 2.5/sin 41° {cross multiplication}
x = 3.8106
Therefore, the value of the side labelled x is equal to 3.8 to the nearest tenth using the trigonometric ratio of sine.
Read more about trigonometric ratios here: https://brainly.com/question/3457795
#SPJ1
can someone help me with this

Answers
Step-by-step explanation:
1. cd and dg
2. angle 2
3. angle gde
4. angle cdh
5. cde is st line
6.cdf = cdh+hdf = 42+117= 159
7. angle fde = 90-73=17
the question is 4 1/5 x 5/14
Answers
Answer:
3/2
Step-by-step explanation:
Simplify the following:
((4 + 1/5)×5)/14
((4 + 1/5)×5)/14 = ((4 + 1/5)×5)/14:
((4 + 1/5)×5)/14
Put 4 + 1/5 over the common denominator 5. 4 + 1/5 = (5×4)/5 + 1/5:
(((5×4)/5 + 1/5) 5)/14
5×4 = 20:
((20/5 + 1/5)×5)/14
20/5 + 1/5 = (20 + 1)/5:
(((20 + 1)/5)×5)/14
20 + 1 = 21:
(21/5×5)/14
21/5×5 = (21×5)/5:
((21×5)/5)/14
((21×5)/5)/14 = (21×5)/(5×14):
(21×5)/(5×14)
(21×5)/(5×14) = 5/5×21/14 = 21/14:
21/14
The gcd of 21 and 14 is 7, so 21/14 = (7×3)/(7×2) = 7/7×3/2 = 3/2:
Answer: 3/2
Will give 80 points!
Method of Travel to School
Walk/Bike Bus Car Row totals
Under age 15 60 165
Age 15 and above 65 195
Column totals 152 110 98 360
What percentage of students under age 15 travel to school by car? Round to the nearest whole percent.
11%
18%
41%
Answers
Answer:
There are about 80 students age 15 and above take a car to school.
Step-by-step explanation:
1. For all the columns the total has been given.
2. Bus is taken as 60 as walk/bike has been given 65 under age 15.
3. 195 row total Age 15 and above has been provided and updated.
4. Walk/Bike 152, 65 is already given Age 15 and above difference is 87.
5. Bus 60 under age 15 is already given total 110 difference is 50.
6. Age 15 and above 65,50,195 (Total) is already given row difference is 80.
7. Car is Age 15 and above is 80 and Total column is 98 difference is 18.
8. Age 15 and above take car is 80.

Answer:
its 41%
Step-by-step explanation:
i took the test
A relative frequency table is made from data in a frequency table.What is the value of k in the relative frequency table? Round the answer to the nearest percent. 2% 11% 20% 33%
Answers
Sir where is the table.
Solve the inequality (3+2x)-4>9 Express the solution in set notation.
Answers
Answer:x > 15
Step-by-step explanation:
simplify both sides of the inequality
2x + 9 > 39
subtract 9 from both sides
2x + 9 - 9 > 39 -9
2x > 30
divide both sides by 2
2x/2 > 30/2
x > 15
Brainliest please
8. Dylan has 35 coins in his pocket. All of them are either pennies or quarters, and
they total $4.43. How many of each coin does he have?
Answers
Because 17*0.25=4.25 and 18*0.01=0.18.
4.25+0.18=4.43 also 17+18=35
Solve for the unknown. q- 5/6=1 5/6
Answers
Answer:
q=8/3
Step-by-step explanation:
First, add 5/6 to both sides to get rid of -5/6 to get q=16/6 then simplify to q=8/3.
Answer:
\(q=2\frac{2}{3}\)
Step-by-step explanation:
The given equation consists of a fraction and a mixed number.
First, convert the mixed number into an improper fraction by multiplying the whole number by the denominator of the fraction, adding this to the numerator of the fraction, and placing the answer over the denominator:
\(q-\dfrac{5}{6}=1 \frac{5}{6}\)
\(q-\dfrac{5}{6}=\dfrac{1 \cdot 6+5}{6}\)
\(q-\dfrac{5}{6}=\dfrac{11}{6}\)
Now, add 5/6 to both sides of the equation to isolate q:
\(q-\dfrac{5}{6}+\dfrac{5}{6}=\dfrac{11}{6}+\dfrac{5}{6}\)
\(q=\dfrac{11}{6}+\dfrac{5}{6}\)
As the fractions have the same denominator, we can carry out the addition by simply adding the numerators:
\(q=\dfrac{11+5}{6}\)
\(q=\dfrac{16}{6}\)
Reduce the improper fraction to its simplest form by dividing the numerator and denominator by the greatest common factor (GCF).
The GCF of 16 and 6 is 2, therefore:
\(q=\dfrac{16\div 2}{6 \div 2}\)
\(q=\dfrac{8}{3}\)
Finally, convert the improper fraction into a mixed number by dividing the numerator by the denominator:
\(q=2 \; \textsf{remainder}\;2\)
The mixed number answer is the whole number and the remainder divided by the denominator:
\(q=2\frac{2}{3}\)
e
B
0
14. The table shows the number of inches of
rain over five months. What would be an
appropriate display of the data? Explain.
(Lesson 2)
Month
Number
of Inches
of Rain
Jan. Feb. Mar.
1.5
2.2
3.6
Apr.
5.3
May
4.8

Answers
The graph of the given function is attached.
Given is a function for the rainfall in 5 months in inches.
We need to display the data,
So, as we can see that the data is not showing any proportion or pattern,
So, it can be displayed as a line chart.
Hence the chart is attached for the function.
Learn more about line chart click;
https://brainly.com/question/29359235
#SPJ1

Workout to the simplest:
\( \int \: {x}^{2} ln( {x}^{3} ) dx\)
Answers
Answer:
\(\rm \displaystyle \ln(x) { {x}^{3} } - \frac{ {x}^{3} }{3} + \rm C\)
Step-by-step explanation:
we would like to integrate the following integration
\( \displaystyle \int {x}^{2} \ln( {x}^{3} ) dx\)
before doing so we can use logarithm exponent rule in order to get rid of the exponent of ln(x³)
\( \displaystyle \int 3 {x}^{2} \ln( {x}^{} ) dx\)
now notice that the integrand is in the mutilation of two different functions thus we can use integration by parts given by
\( \rm\displaystyle \int u \cdot \: vdx = u \int vdx - \int u' \bigg( \int vdx \bigg)dx\)
where u' can be defined by the differentiation of u
first we need to choose our u and v in that case we'll choose u which comes first in the guideline ILATE which full from is Inverse trig, Logarithm, Algebraic expression, Trigonometry, Exponent.
since Logarithms come first our
\( \displaystyle u = \ln(x) \quad \text{and} \quad v = {3x}^{2} \)
and u' is \(\frac{1}{x}\)
altogether substitute:
\( \rm \displaystyle \ln(x) \int 3{x}^{2} dx - \int \frac{1}{x} \left( \int 3 {x}^{2} dx \right)dx\)
use exponent integration rule to integrate exponent:
\( \rm \displaystyle \ln(x) \int 3{x}^{2} dx - \int \frac{1}{x} \left( 3\frac{ {x}^{3} }{3} \right)dx\)
once again exponent integration rule:
\( \rm \displaystyle \ln(x) 3\frac{ {x}^{3} }{3} - \int \frac{1}{x} \left( 3\frac{ {x}^{3} }{3} \right)dx\)
simplify integrand:
\( \rm \displaystyle \ln(x) 3\frac{ {x}^{3} }{3} - \int \frac{ 3{x}^{3} }{3x} dx\)
use law of exponent to simplify exponent:
\( \rm \displaystyle \ln(x) \frac{ 3{x}^{3} }{3} - \int \frac{ 3\cancel{ {x}^{3}} }{3 \cancel{x}} dx\)
\( \rm \displaystyle \ln(x) \frac{ 3{x}^{3} }{3} - \int \frac{ 3{x}^{3} }{3} dx\)
use constant integration rule to get rid of constant:
\(\rm \displaystyle \ln(x) \frac{3 {x}^{3} }{3} - 1 \int {x}^{2}dx\)
use exponent integration rule:
\(\rm \displaystyle \ln(x) \frac{3 {x}^{3} }{3} - \frac{ {x}^{3} }{3} \)
\(\rm \displaystyle \ln(x) { {x}^{3} } - \frac{ {x}^{3} }{3} \)
and finally we of course have to add the constant of integration:
\(\rm \displaystyle \ln(x) { {x}^{3} } - \frac{ {x}^{3} }{3} + \rm C\)
and we are done!
Express in set builder notation the set of numbers that is indicated on the number line

Answers
The numbers indicated on the number line are:
\(-3,-2,-1,0,1,2,3,4\)The given numbers are all integers.
Therefore, the set of the given numbers expressed in set builder notation is as follows:
\(\lbrace x|-3\leq x\leq4\text{ and }x\in\text{ Integers}\rbrace\){x| -3 ≤ x ≤ 4 and x ∈ Integers}
Please help!! I'll give 50 points
Solve the system of equations.
2x + 9y = 6
-7x - 8y = -21
Answers
Answer: y=0 and x=3
Step 1: Solve for x in 2x+9y=6.
\(2x+9y=6\)
\(2x=6-9y\) (Subtract 9y from both sides)
\(x=3 - 4.5y\)( Divide both sides by 2)
Step 2: Replace x with 3-4.5y
\(-7x - 8y = -21\\-7(3-4.5y) - 8y = -21\\\)
Step 3: Solve for y
\((-21)+31.5y-8y=(-21)\) (By looking at this, we can determine that y=0)
Step 4: Replace y with 0
\(2x+9y=6\\2x+9(0)=6\\2x=6\\\)
\(x=3\) (Divide both sides 2)
Therefore, y=0 and x=3
Answer: y=0 and x=3
Step-by-step explanation:
yo yo buddy i got yo bro yo buddy i

Answers
Answer: \(=1\frac{111}{125}\)
Step-by-step explanation:
\(=1+0.888\)
\(=1+\frac{111}{125}\)
\(=1\frac{111}{125}\)
yuhhhhhhhhhhhhhhhhhhhhhhhhhhhhhh
What’s the mean of 46,57,66,63,49,52,61,68
Answers
Answer:
Step-byHow do I calculate the mean?
The mean can be calculated only for numeric variables, no matter if they are discrete or continuous. It's obtained by simply dividing the sum of all values in a data set by the number of value
-step explanation:
46+57+66+63+49+52+61+68= 462/8 the total number of observation
the answer 57
the answer 57
Write an equation that represents the perimeter of the rectangle. The width of a rectangle is 9 less than one-third it's width, when the perimeter is 45.
Answers
Answer:
The equation that represents the perimeter of the rectangle is:
\(\text{Perimeter} = \frac{2}{3} \times [4l-27]\)
Step-by-step explanation:
The perimeter of a rectangle is given by the formula:
Perimeter = 2 × [l + w]
It is provided that the width of a rectangle is 9 less than one-third it's length.
That is:
\(w = \frac{1}{3}l-9\)
The perimeter is given as 45.
The equation that represents the perimeter of the rectangle is:
\(\text{Perimeter} = 2 \times [l + \frac{1}{3}l-9]\\\\\text{Perimeter} = 2 \times [\frac{3l+l-27}{3}]\\\\\text{Perimeter} = 2 \times [\frac{4l-27}{3}]\\\\\text{Perimeter} = \frac{2}{3} \times [4l-27]\)
Thus, the equation that represents the perimeter of the rectangle is:
\(\text{Perimeter} = \frac{2}{3} \times [4l-27]\)
name the angle relationship.the choices are a. vertical b. corresponding c. alternate interior d. linear pair

Answers
Solution
For this case we can conclude that angle 2 and angle 1 are:
b. corresponding
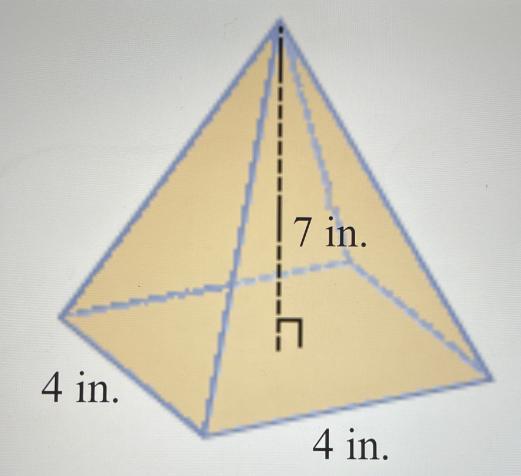
find the volume of the square pyramid. type an integer or decimal. round final answer to nearest tenth as needed.

Answers
Answer:
Explanation:
Given:
To find:
The volume of the square pyramid
The volume(V) of a square pyramid can be determined using the below formula;
\(V=a^2\frac{h}{3}\)where a = length of the side of the square base = 4 in
h = height of the pryramid = 7 in
So if we substitute the above values into the formula and solve for V, we'll have;
\(\begin{gathered} V=4^2\frac{7}{3} \\ =16*\frac{7}{3} \\ =37.3\text{ in}^3 \end{gathered}\)So the volume of the square pyramid is 37.3 in^3
3/8 + 1/8 - 1/6 + 1/4 =
Answers
1/2+1/4=3/4 since denominator is 4 and numerator is (2*1)+(1*1)=3
3/4-1/6=7/12 since denominator is 12 and numerator is (3*3)-(2*1)=7
Final answer is 7/12
HELP ASAP! (VERY EASY)
Which of the following is the fourth vertex needed to create a rectangle with vertices located at (5, 6), (9, 6), and (5, 3)?
(5, –6)
(5, –3)
(9, –6)
(9, 3)
Answers
The fourth vertex such that it forms a right angle with two adjacent vertices the correct answer is \((9, 3)\) . Thus, option D is correct.
What is the adjacent vertices?To create a rectangle, we need to find the fourth vertex such that it forms a right angle with two adjacent vertices. We can use the distance formula to determine the length of each side of the triangle formed by the three given vertices:
The distance between \((5, 6)\) and \((9, 6)\) is \(4\) units.
The distance between \((5, 6)\) and \((5, 3)\) is \(3\) units.
The distance between \((9, 6)\) and \((5, 3)\) is \(5\) units.
Since the two sides with length 4 units are adjacent and form a right angle, we know that the fourth vertex must be located 3 units below (9, 6) or 3 units above (5, 3). Therefore, the fourth vertex can be either (9, 3) or (5, 9).
However, only \((9, 3)\) forms a rectangle with the three given vertices, as it is also 5 units away from \((5, 6)\) and \(4\) units away from (9, 6), forming a right angle with both.
Therefore, the correct answer is \((9, 3)\).
Learn more about vertices here:
https://brainly.com/question/30116773
#SPJ1
How many shipments had at least 10 broken tiles but less than 20 broken tiles ?

Answers
Answer:
5 shipments had at least 10 broken tiles but less than 20 broken tiles.
I need help with this!

Answers
The length AC in the kite is 8.7 cm.
How to find the side AC in the kite?A kite is a quadrilateral that has two pairs of consecutive equal sides and
perpendicular diagonals. Therefore, let's find the length AC in the kite.
Hence, using Pythagoras's theorem, let's find CE.
Therefore,
7² - 4² = CE²
CE = √49 - 16
CE = √33
CE = √33
Let's find AE as follows:
5²- 4² = AE²
AE = √25 - 16
AE = √9
AE = 3 units
Therefore,
AC = √33 + 3
AC = 5.74456264654 + 3
AC = 8.74456264654
AC = 8.7 units
learn more on kite here: https://brainly.com/question/27975644
#SPJ9