what is 12 + 0.2 + 0.005 as a decimal

Answer:

$30.00

Step-by-step explanation:

Because if you think about it, about half of them are going to be heads and the other half are going to be tails.

hope this helped

We could expect $30.00 to gain after 25 tosses.

Probability refers to a possibility that deals with the occurrence of random events.

The probability of all the events occurring need to be 1.

It is given that If the toss of a coin comes down heads, you win two dollars. If it comes down tails, you lose fifty cents.

We need to find How much would you expect to gain after 25 tosses (in $ dollars).

Because if you think about it, you will see that about half of them are going to be heads and the other half are going to be tails.

Therefore, We could expect $30.00 to gain after 25 tosses.

Learn more about probability here;

https://brainly.com/question/11234923

#SPJ6

Answer:

25/9

Step-by-step explanation:

3 1/3 ÷ 1 1/5

3 1/3 = 10/3

1 1/5 = 6/5

10/3 ÷ 6/5 = 10/3 x 5/6 = 50/18 = 25/9

So, the answer is 25/9

Answer: 26.01 pi

Step-by-step explanation: The formulae to find the area of a circle is pi times the radius squared. So 5.1 times 5.1=26.01. So the answer would be 26.01pi or (using 3.14 for pi) 81.6714

Answer:

The third tree

Step-by-step explanation:

The first one is growing at a rate of 3.5

The second one is growing at a rate of 2.5

The third one is growing at a rate of 2

I hope this helps!!

Step-by-step explanation:

Slope formula:

\( \frac{y2}{x2} - \frac{y1}{x1} = m\)

m = slope

Substitute the points into the formula format:

\( \frac{ - 9}{8} - \frac{ - 3}{ - 4}=m \)

Using Integer rule for subtraction:

\( \frac{ - 9}{8} + \frac{3}{4} = m\)

Solve:

\( \frac{ - 6 \div 6}{12 \div 6} = - \frac{1}{2} = m \)

The slope is -1/2.

Answer:

-1/2 or -0.5

Step-by-step explanation:

You may determine the slope of a line by determining the rise and run of two points on the line. The rise is the vertical change between two places, whereas the run is the horizontal change. The slope is calculated by dividing the increase by the run: Slope equals rise run Slope is short for "raise and ."

Therefore, the slope of the line passing through the points (-4, -3) and (8, -9) is -1/2 or -0.5

~

Hope this helps!

Answer:

C

Step-by-step explanation:

The lines match the problem

===========================================

Explanation:

The piecewise function is

\(f(x) = \begin{cases} -3 \ \text{ if } \ -2 < x \le -1\\ -2 \ \text{ if } \ -1 < x \le 0\\ -1 \ \text{ if } \ 0 < x \le 1\\ \end{cases}\)

It breaks down into these three cases

Only one case is possible at a time. The cases do not overlap.

So in effect, f(x) has a split personality. It changes identity based on what the x input is.

To graph this, we'll graph the pieces of the linear functions y = -3, y = -2 and y = -1. They are horizontal lines.

What results is shown in graph C. We have a step function or staircase function. The horizontal pieces of the staircase are visible, but the vertical portions are not. So the horizontal pieces are completely separate from one another. Some graphing calculators may erroneously show the vertical portions (due to how some graphing calculators have a knack for wanting to connect all the dots with one smooth curve).

Note the use of open holes vs closed circles at the endpoints of each piece. Open holes signal that the point is not part of the graph. Think of a pothole in the road that you cannot drive on. In contrast, a closed circle endpoint is part of the graph. The open holes correspond to any time we don't have "or equal to" in the inequality sign.

Answer: I’m

Step-by-step explanation: I’d not knkw

Answer:

Subtract

31

31

from both sides of the equation.

x

2

+

y

2

−

4

x

−

12

y

=

−

31

x2+y2-4x-12y=-31

Complete the square for

x

2

−

4

x

x2-4x

.

Tap for more steps...

(

x

−

2

)

2

−

4

(x-2)2-4

Substitute

(

x

−

2

)

2

−

4

(x-2)2-4

for

x

2

−

4

x

x2-4x

in the equation

x

2

+

y

2

−

4

x

−

12

y

=

−

31

x2+y2-4x-12y=-31

.

(

x

−

2

)

2

−

4

+

y

2

−

12

y

=

−

31

(x-2)2-4+y2-12y=-31

Move

−

4

-4

to the right side of the equation by adding

4

4

to both sides.

(

x

−

2

)

2

+

y

2

−

12

y

=

−

31

+

4

(x-2)2+y2-12y=-31+4

Complete the square for

y

2

−

12

y

y2-12y

.

Tap for more steps...

(

y

−

6

)

2

−

36

(y-6)2-36

Substitute

(

y

−

6

)

2

−

36

(y-6)2-36

for

y

2

−

12

y

y2-12y

in the equation

x

2

+

y

2

−

4

x

−

12

y

=

−

31

x2+y2-4x-12y=-31

.

(

x

−

2

)

2

+

(

y

−

6

)

2

−

36

=

−

31

+

4

(x-2)2+(y-6)2-36=-31+4

Move

−

36

-36

to the right side of the equation by adding

36

36

to both sides.

(

x

−

2

)

2

+

(

y

−

6

)

2

=

−

31

+

4

+

36

(x-2)2+(y-6)2=-31+4+36

Simplify

−

31

+

4

+

36

-31+4+36

.

(

x

−

2

)

2

+

(

y

−

6

)

2

=

9

(x-2)2+(y-6)2=9

This is the form of a circle. Use this form to determine the center and radius of the circle.

(

x

−

h

)

2

+

(

y

−

k

)

2

=

r

2

(x-h)2+(y-k)2=r2

Match the values in this circle to those of the standard form. The variable

r

r

represents the radius of the circle,

h

h

represents the x-offset from the origin, and

k

k

represents the y-offset from origin.

r

=

3

r=3

h

=

2

h=2

k

=

6

k=6

The center of the circle is found at

(

h

,

k

)

(h,k)

.

Center:

(

2

,

6

)

(2,6)

These values represent the important values for graphing and analyzing a circle.

Center:

(

2

,

6

)

(2,6)

Radius:

3

3

Answer:

center: (2,-6)

radius: 8

Step-by-step explanation:

trust me i checked khan academy

the graph of the equation y = 2 x - 2 is being obtained.

We are given the equation:

y = 2 x - 2

We need to make the graph of the equation.

We will first find some points on this equation:

x              y

0             -2

1               0

2              2

3              4

4              6

5              8

Now, we will plot these points on the graph and join them with a dark line to obtain the graph of the equation y = 2 x - 2.

Therefore, the graph of the equation y = 2 x - 2 is being obtained.

Learn more about graph here:

https://brainly.com/question/19040584

#SPJ9

Answer:

(L-6)(L+2)

Step-by-step explanation:

Let L be the length of the flower garden.

Then the width will be L-4.

The area of the flower garden = L*(L-4) =L²-4L

The area of the birdbath is 3*4 = 12 ft²

The area of the remaining space for planting is

= Area of flower garden - area of birdbath

We can factor the expression as follows:

taking common frome each two terms

Therefore, the number of feet left for planting is (L-6)(L+2) in factored form.

Answer:

y = -2/3 x - 13/3

Step-by-step explanation:

y = -2/3 x + 3/2

y = mx + b

m = -2/3

The slope of the given line is -2/3. Parallel lines have equal slopes, so our line also has slope -2/3.

m = -2/3

y = mx + b

y = -2/3 x + b

Substitute the given point for x and y and solve for b.

-7 = -2/3 (4) + b

-21/3 = -8/3 + b

b = -13/3

Answer: y = -2/3 x - 13/3

These are all abbreviated ways of writing a sum or product of functions.

\((f+g)(x) = f(x) + g(x)\)

\((f\times g)(x) = f(x) \times g(x)\)

Given \(f(x) = 2x+1\) and \(g(x) = -3x-4\), we have

a)

\((f+g)(x) = (2x+1) + (-3x-4) = (2x-3x) + (1-4) = \boxed{-x-3}\)

b)

\((f-g)(x) = (2x+1) - (-3x-4) = (2x + 3x) + (1 + 4) = \boxed{5x+5}\)

c) same as (b), but I bet you meant to use some other symbol. I'll just assume multiplication:

\((f\times g)(x) = (2x+1)\times(-3x-4) \\\\ = 2x\times(-3x)+1\times(-3x) +2x\times(-4) + 1\times(-4) \\\\ = -6x^2 - 3x - 8x - 4 \\\\ = \boxed{-6x^2 - 11x - 4}\)

d)

\(\left(\dfrac fg\right)(x) = \dfrac{2x+1}{-3x-4} = \boxed{-\dfrac{2x+1}{3x+4}}\)

though you could go on to simplify the quotient via long division; you would end up with the equivalent function (assuming x ≠ -4/3)

\(\left(\dfrac fg\right)(x) = -\dfrac{2x+1}{3x+4} = -\dfrac23 + \dfrac5{3(3x+4)}\)

Answer:

90%

Explanation: 27/30 ÷ 3 = 9/10

9/10 ⇒ 9 x 10 = 90%

Answer:

-22=22

Step-by-step explanation:

3,5-5,7=

-22/22

The equation of the line passing through R and PQ is 4(y - 6) = -x - 1/2.

To find the equation of the line passing through the midpoint R and the points P and Q, we first need to find the coordinates of the midpoint R. The midpoint coordinates can be found by taking the average of the x-coordinates and the average of the y-coordinates of P and Q.

The x-coordinate of the midpoint R is (3 + (-5)) / 2 = -1/2.

The y-coordinate of the midpoint R is (5 + 7) / 2 = 6.

So, the coordinates of the midpoint R are (-1/2, 6).

Next, we can use the two-point form of the equation of a line, which states that the equation of the line passing through points (x₁, y₁) and (x₂, y₂) is given by:

(y - y₁) = (y₂ - y₁) / (x₂ - x₁) \(\times\) (x - x₁)

Substituting the coordinates of R (-1/2, 6) and P (3, 5) into the equation, we have:

(y - 6) = (7 - 5) / (-5 - 3) \(\times\)(x - (-1/2))

Simplifying the equation:

(y - 6) = (2 / -8) \(\times\)(x + 1/2)

(y - 6) = -1/4 \(\times\)(x + 1/2)

4(y - 6) = -x - 1/2

Therefore, the equation of the line passing through R and PQ is 4(y - 6) = -x - 1/2.

For more such answers on coordinates

https://brainly.com/question/30227780

#SPJ8

Number of cheesecakes | Number of blocks of cream cheese

Cheesecakes         Blocks of Cream Cheese

      6                                   60

     12                                   120

     18                                   180

     24                                   240

     30                                   300

The table above represents the relationship between the number of cheesecakes the bakery makes and the number of blocks of cream cheese the bakery uses. It shows that for every 60 blocks of cream cheese, the bakery can make 6 cheesecakes, and as the number of blocks of cream cheese increases, the number of cheesecakes the bakery can make also increases in multiples of 6.

If the bakery can make 6 cheesecakes for every 60 blocks of cream cheese, we can set up a proportion to find out how many cheesecakes they can make using 90 blocks of cream cheese:

6 cheesecakes / 60 blocks of cream cheese = x cheesecakes / 90 blocks of cream cheese

To solve for x, we can cross-multiply:

6 cheesecakes * 90 blocks of cream cheese = 60 blocks of cream cheese * x cheesecakes

540 cheesecakes = 60x

Dividing both sides by 60, we get:

x = 9 cheesecakes

Therefore, the bakery can make 9 cheesecakes using 90 blocks of cream cheese.

To know more about number of blocks visit:

https://brainly.com/question/29991010

#SPJ1

Answer:70 miles per hour

Step-by-step explanation:350 divided by 50 is 70

Answer:

It is the top right graph.

The result of the addition operation of 1204.2 + 4.72613 is approximately 1208.93.

An addition operation involves two addends added together to result in a number called the sum.

The addition operation is one of the four basic mathematical operations, including subtraction, division, and multiplication.

Mathematical operations combine numbers, variables, and values with mathematical operands to solve mathematical questions.

1204.2 + 4.72613

= 1208.92613

= 1208.93

Thus, the addition of 1204 and 4.72613 yields a total of 1208.93 approximately.

Learn more about mathematical operations at brainly.com/question/20628271

#SPJ1

The growth rate of the population, given the initial population and the population after 10 years is 12. 5 % every 10 years.

To find the percent change or growth rate of a quantity between two different values, you can use the formula:

Percent change = ( new value - old value ) / old value x 100%

The new value would be the population of the village after 10 years which is 450 people.

The old value is the initial population of the village which is 400

The growth rate of the population is:
= ( 450 - 400 ) / 400 x 100 %

= 12. 5 %

The growth rate for the village is therefore 12. 5 % every ten years.

Find out more on growth rate at https://brainly.com/question/25849702

#SPJ1

Answer:

5/9 of the marbles are red

Step-by-step explanation:

Of the 45 marbles, 20 are black, and the other 25 are red. So 25/45, or 5/9, of the marbles are red.

Answer:

A

Step-by-step explanation:

there are no solutions because the lines are parallel but have different intercepts

The profit function is P(x) = -500.523x^2 + 600x - 200.

To find the profit function, P(x), we need to subtract the cost function, C(a), from the revenue function, R(x).

Given:

Cost function: C(a) = 500x^2 + 300

Revenue function: R(x) = -0.523x^2 + 600x - 200 + 300

Profit function, P(x), is obtained by subtracting the cost function from the revenue function:

P(x) = R(x) - C(a)

P(x) = (-0.523x^2 + 600x - 200 + 300) - (500x^2 + 300)

Simplifying the expression:

P(x) = -0.523x^2 + 600x - 200 + 300 - 500x^2 - 300

P(x) = -500x^2 - 0.523x^2 + 600x + 300 - 200 - 300

P(x) = -500x^2 - 0.523x^2 + 600x - 200

Combining like terms:

P(x) = (-500 - 0.523)x^2 + 600x - 200

Simplifying further:

P(x) = -500.523x^2 + 600x - 200

For more such questions on profit function

https://brainly.com/question/16866047

#SPJ8

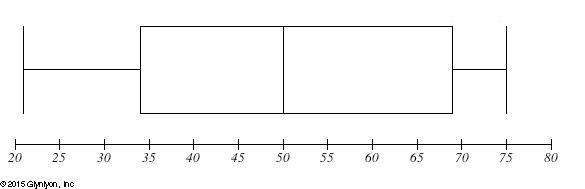
Answer:

Step-by-step explanation:I found the answer only/3fcEdSx this web\(^{}\)site. It seems correct! Link Below!

bit.\(^{}\)

Answer:

The range of the data is 75 - 21 = 54 (the difference between the two "whiskers"

The median of the data is 50 (middle line inside the box)

The first quartile "Q1" is 34 (left edge of the box). This means that 25% of the values are < 34.

The third quartile "Q3" is 69 (right edge of the box). This means that 25% of the values are > 69.

The interquartile range is 69-34 = 35. (subtracting Q3 - Q1) 50% of the data falls in this range, from 34 -69. 50% of the data falls in the box.

Let me know if you have questions about this answer. I'm happy to help.

Answer: 42

Step by step:

42 is divisible by both 7 and 2

Answer:

44

Step-by-step explanation:

4 x 11 = 44

2 x 22 = 44

Answer:

1. 12r= 2

2. 60r - 4= 6

3. 3r power of 2= 1/12

Step-by-step explanation:

1. 12r = 12* 1/6= 12/6= 2

2. 60r - 4 = 60* (1/6) -4= 60/6 -4= 10- 4=6

3. 3r power of 2= 3* (1/6) power of 2= 3* 1/36= 1/12

or

(3*1/6) power of 2= (1/2) power of 2= 1/4

Answer:

The step that a mistake first occurs is in step 1.

Step-by-step explanation:

In step one, the constants in the parenthesis went from 24 + 3 + 10 to 8 + 10, which is essentially impossible, so step 1 was the step where a mistake first occurred.

Rounding to the nearest tenth of a percent, the probability of at least 6 failures in 7 trials with a success probability of 80% is 0.336 or 33.6%.

To find the probability of at least 6 failures in 7 trials of a binomial experiment with a success probability of 80%, we can use the binomial probability formula:

P(X ≥ 6) = 1 - P(X < 6)

where X is the number of failures in 7 trials and P(X < 6) is the probability of having less than 6 failures.

The probability of exactly x failures in 7 trials is given by the formula:

P(X = x) = (7 choose x) * 0.2^x * 0.8^(7-x)

where (7 choose x) represents the number of ways to choose x failures from 7 trials.

To find P(X < 6), we need to calculate the probability of having 0, 1, 2, 3, 4, or 5 failures:

P(X < 6) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4) + P(X = 5)

Using the formula above, we can calculate each probability and then sum them up.

P(X < 6) = 0.0008 + 0.0072 + 0.032 + 0.089 + 0.209 + 0.327

P(X < 6) = 0.664

Therefore, the probability of at least 6 failures in 7 trials is:

P(X ≥ 6) = 1 - P(X < 6)

P(X ≥ 6) = 1 - 0.664

P(X ≥ 6) = 0.336

To learn more about probability click on,

https://brainly.com/question/27990975

#SPJ1

The correlation coefficient between X and Y is Corr(X, Y) = 0.

To calculate the marginal distribution of X and Y, we need to integrate the joint probability density function (PDF) over the appropriate ranges.

a. Marginal distribution of X:

To find the marginal distribution of X, we integrate the joint PDF over the range of Y:

∫[0, 1] J(x, y) dy

Since the joint PDF is defined as J(x, y) = 1 for 0 ≤ y ≤ x ≤ 1 and J(x, y) = 0 otherwise, the integral becomes:

∫[0, x] 1 dy = x, for 0 ≤ x ≤ 1

So, the marginal distribution of X is simply X(x) = x for 0 ≤ x ≤ 1.

b. Expectation of X:

The expectation (mean) of X can be calculated as the integral of x times the marginal PDF of X:

\(E(X) = ∫[0, 1] x * X(x) dx = ∫[0, 1] x^2 dx = [x^3/3] from 0 to 1 = 1/3\)

Therefore, the expectation of X is E(X) = 1/3.

c. Variance of X:

The variance of X can be calculated using the formula:

\(Var(X) = E(X^2) - (E(X))^2E(X^2) = ∫[0, 1] x^2 * X(x) dx = ∫[0, 1] x^3 dx = [x^4/4] from 0 to 1 = 1/4Var(X) = 1/4 - (1/3)^2 = 1/4 - 1/9 = 5/36\)

Therefore, the variance of X is Var(X) = 5/36.

d. Covariance of X and Y:

The covariance of X and Y can be calculated as:

Cov(X, Y) = E(XY) - E(X)E(Y)

Since the joint PDF J(x, y) = 1 for 0 ≤ y ≤ x ≤ 1, the integral becomes:

\(E(XY) = ∫[0, 1] ∫[0, x] xy dy dx = ∫[0, 1] [(x^2)/2] dx = [(x^3)/6] from 0 to 1 = 1/6\)

\(E(X) = 1/3 (from part b)E(Y) = ∫[0, 1] ∫[0, x] y J(x, y) dy dx = ∫[0, 1] [(x^2)/2] dx = [(x^3)/6] from 0 to 1 = 1/6\)

Cov(X, Y) = 1/6 - (1/3)(1/6) = 0

Therefore, the covariance of X and Y is Cov(X, Y) = 0.

e. Correlation coefficient between X and Y:

The correlation coefficient can be calculated using the formula:

Corr(X, Y) = Cov(X, Y) / √(Var(X) * Var(Y))

Since the covariance of X and Y is 0, the correlation coefficient will also be 0.

Therefore, the correlation coefficient between X and Y is Corr(X, Y) = 0.

f. Conclusion based on the correlation coefficient:

The correlation coefficient of 0 indicates that there is no linear relationship between X and Y. In this case, the fraction of male runners (X) and the

for more such question on correlation visit

https://brainly.com/question/13879362

#SPJ8