What is 1.8 rounded to the nearest tenth
Answers
Answer: 1.8 rounded to the nearest tenth will remain as 1.8 because 0.8 is 8 tenths
Answer:
Step-by-step explanation:
11.3
Related Questions
Suppose it is desired to estimate the average time a customer spends in Dollar Tree to within 5 minutes at 99% reliability. It is estimated that the standard deviation of the times is 15 minutes. How large a sample should be taken to get the desired interval?
Answers
Answer:
Im not sure how to explain this but text me so i can fully explain it to where you understand
Step-by-step explanation:
Helpppppppppppppp:))))

Answers
Given:
Principal value = $1500
Rate of interest = 7% per annum compounded daily
Time = 2 years.
To find:
The amount after 2 years.
Solution:
Formula for amount:
\(A=P\left(1+\dfrac{r}{n}\right)^{nt}\)
Where, P is principal, r is the rate of interest in decimals, n is the number of time interest compounded in an year and t is the number of years.
We know that 1 year is equal to 365 days and the interest compounded daily. So, n=365.
Substituting \(P=1500,\ r=0.07,\ n=365,\ t=2\) in the above formula, we get
\(A=1500\left(1+\dfrac{0.07}{365}\right)^{365(2)}\)
\(A=1500\left(\dfrac{365+0.07}{365}\right)^{730}\)
\(A=1500\left(\dfrac{365.07}{365}\right)^{730}\)
Using calculator, we get
\(A\approx 1725.39\)
The amount after two years is $1,725.39. Therefore, the correct option is (c).
Find the value of x. Write your answer in simplest form.

Answers
Answer:
\(x = \frac{9}{ \sqrt{2} } = \frac{9 \sqrt{2} }{2} \)
Find a set of four integers such that their order and the order of their absolute valúes are the same
Answers
The set of 4 integers are is given by the equation A = { 1 , 2 , 3 , 4 }
What is an Equation?Equations are mathematical statements with two algebraic expressions flanking the equals (=) sign on either side.
It demonstrates the equality of the relationship between the expressions printed on the left and right sides.
Coefficients, variables, operators, constants, terms, expressions, and the equal to sign are some of the components of an equation. The "=" sign and terms on both sides must always be present when writing an equation.
Given data ,
Let the set of 4 integers be represented as set A
Now , the equation will be
Let the first number be 1
The absolute value of 1 is | 1 | = 1
Let the second number be 2
The absolute value of 2 is | 2 | = 2
Let the third number be 3
The absolute value of 3 is | 3 | = 3
Let the fourth number be 4
The absolute value of 4 is | 4 | = 4
And , | 1 | < | 2 | < | 3 | < | 4 |
Hence , the set of integers are { 1 , 2 , 3 , 4 }
To learn more about equations click :
https://brainly.com/question/13458566
#SPJ1
Pls help quick………… Math

Answers
what is square root of 64?
Answers
Answer:
8
Step-by-step explanation:
8*8=64
O
X
y
X
y
X
y
X
y
0
2
0
0
-1
0
1
0
5
2
113
1
2
2
8
4
WIN
3
3
4
11
2.5 -2.5-7.5 -12.5
6
W/W
5
6
Select all table’s that represent proportional relationship between x and y
Answers
All tables that represent proportional relationship between x and y are:
B. table B.
E. table E.
What is a proportional relationship?In Mathematics and Geometry, a proportional relationship is a type of relationship that produces equivalent ratios and it can be modeled or represented by the following mathematical equation:
y = kx
Where:
y represents the x-variable.x represents the y-variable.k is the constant of proportionality.Next, we would determine the constant of proportionality (k) by using various data points as follows:
Constant of proportionality, k = y/x
Constant of proportionality, k = (20 - 15)/(10 - 5) = (5 - 4)/(1 - 0)
Constant of proportionality, k = 1.
Therefore, the required linear equation is given by;
y = kx
y = x
Read more on proportional relationship here: brainly.com/question/28350476
#SPJ1
Missing information:
The question is incomplete and the complete question is shown in the attached picture.

determine the inclination of the following straight line
1. y=x+3 2) 3x-2y = 6
Answers
The inclination of the line represented by the equation y = x + 3 is 1, and the inclination of the line represented by the equation 3x - 2y = 6 is 3/2.
To determine the inclination (or slope) of a straight line, we can examine the coefficients of the variables x and y in the equation of the line.
The inclination represents the ratio of how much y changes with respect to x.
Equation: y = x + 3
In this equation, the coefficient of x is 1, which means that for every increase of 1 in x, y also increases by 1.
This indicates that the inclination of the line is positive, meaning it slopes upwards as x increases.
Since the coefficient of x is 1, the inclination can be expressed as 1/1 or simply 1.
Equation: 3x - 2y = 6
To determine the inclination, we need to rearrange the equation in slope-intercept form (y = mx + b), where m represents the slope.
First, isolate y:
-2y = -3x + 6
Divide the entire equation by -2 to solve for y:
y = (3/2)x - 3
Now we can observe that the coefficient of x is 3/2.
This indicates that for every increase of 1 in x, y increases by 3/2. Therefore, the inclination of this line is positive, indicating an upward slope.
The inclination can be expressed as 3/2.
For similar question on inclination.
https://brainly.com/question/29723347
#SPJ11
In the figure below, two secants are drawn to a circle from exterior point V.
Suppose that VZ=30, VW=45, and VX=22.5. Find XY.
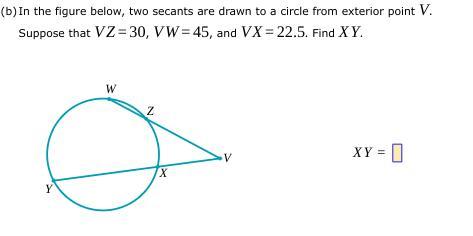
Answers
The value of secant XY is 37.5 units.
How to find the value of secant XY?The Secant-Secant Theorem states that "if two secant segments which share an endpoint outside of the circle, the product of one secant segment and its external segment is equal to the product of the other secant segment and its external segment".
Using the theorem above, we can say:
VZ * VW = VX * VY
30 * 45 = 22.5 * VY
22.5VY = 1350
VY = 1350/22.5
VY = 60 units
Since VY = VX + XY. We have:
60 = 22.5 + XY
XY = 60 - 22.5
XY = 37.5 units
Learn more about Secant-Secant Theorem on:
https://brainly.com/question/30242636
#SPJ1
I need Help please!!!

Answers
Step-by-step explanation:
it seems you solved the tricky part yourself already.
just to be sure, let's do the first derivative here again.
the easiest way would be for me to simply multiply the functional expression out and then do a simple derivative action ...
f(t) = (t² + 6t + 7)(3t² + 3) = 3t⁴ + 3t² + 18t³ + 18t + 21t² + 21 =
= 3t⁴ + 18t³ + 24t² + 18t + 21
f'(t) = 12t³ + 54t² + 48t + 18
and now comes the simple part (what was your problem here, don't you know how functions work ? then you are in a completely wrong class doing derivatives; for that you need to understand what functions are, and how they work). we calculate the function result of f'(2).
we simply put the input number (2) at every place of the input variable (t).
so,
f'(2) = 12×2³ + 54×2² + 48×2 + 18 = 96 + 216 + 96 + 18 =
= 426
(4x-10) x (3x²)
Find the area of the rectangle
Answers
If the length of the rectangle be (3x+2) units and width (4x+10)units then the area of the rectangle be \($x=-\frac{2}{3}, x=-\frac{5}{2}$$\).
How to find the area of rectangle?The region enclosed by an object's shape is referred to as the area. The area of the shape is the area that the figure or any other two-dimensional geometric shape occupies in a plane.
A rectangle's sides determine its area. In essence, the length and breadth of the rectangle multiplied together gives the area of the rectangle.
Let the length of the rectangle be (3x + 2) units and width of the rectangle be (4x + 10)units.
Area of rectangle = length × breadth
= (3x +2) × (4x +10)
simplifying the above equation, we get
= (3x) × (4x +10) + 2(4x +10)
= 12x² + 30x +8x +20
12x² + 38x + 20 = 0
simplifying the above equation, we get
By using quadratic equation, then
\($x_{1,2}=\frac{-38 \pm \sqrt{38^2-4 \cdot 12 \cdot 20}}{2 \cdot 12}$$\)
simplifying the above equation, we get
\($$\begin{gathered}x_{1,2}=\frac{-38 \pm 22}{2 \cdot 12}\end{gathered}$$\)
Separate the solutions, we get
\($$\begin{aligned}& x_1=\frac{-38+22}{2 \cdot 12}, x_2=\frac{-38-22}{2 \cdot 12} \\& x=\frac{-38+22}{2 \cdot 12}:-\frac{2}{3} \\& x=\frac{-38-22}{2 \cdot 12}:-\frac{5}{2}\end{aligned}$$\)
The solutions to the quadratic equation are:
\($x=-\frac{2}{3}, x=-\frac{5}{2}$$\)
The complete question is:
Find the area of rectangle with length (3x+2) units and width (4x+10)units.
To learn more about area refer to:
https://brainly.com/question/2607596
#SPJ1
Which expression correctly represents “eight times the difference of four and a number”? 8 (n minus 4) 8 (4 minus n) 8 (n) minus 4 8 (4) minus n
Answers
Answer:
8(4 - n)
Step-by-step explanation:
Which expression correctly represents “eight times the difference of four and a number”? 8 (n minus 4) 8 (4 minus n) 8 (n) minus 4 8 (4) minus n
Do it one piece at a time.
“eight times the difference of four and a number”: n
“eight times the difference of four and a number”: 4 - n
“eight times the difference of four and a number”: 8(4 - n)
Answer:
the answer is b
Step-by-step explanation:
Find a and b using the factor theorem.
\(f(x)=x^3+ax^2+bx-12\) has factor \((x-1), (x+1)\)
Answers
The values of a and b using the factor theorem for the polynomial f(x), we set f(1) and f(-1) equal to zero. Solving the resulting system of equations, we find that a = 12 and b = -1.
To find the values of a and b using the factor theorem, we need to use the given factors (x - 1) and (x + 1) and the fact that they are roots of the polynomial f(x).
The factor theorem states that if (x - c) is a factor of a polynomial, then f(c) = 0. Therefore, we can set x = 1 and x = -1 in the polynomial f(x) to get two equations.
First, let's substitute x = 1 into f(x):
f(1) = (1)^3 + a(1)^2 + b(1) - 12
f(1) = 1 + a + b - 12
Next, let's substitute x = -1 into f(x):
f(-1) = (-1)^3 + a(-1)^2 + b(-1) - 12
f(-1) = -1 + a - b - 12
Since (x - 1) and (x + 1) are factors, f(1) and f(-1) must equal zero. Therefore, we can set the two equations equal to zero and solve for a and b:
1 + a + b - 12 = 0
-1 + a - b - 12 = 0
Rearraning the equations, we have:
a + b = 11
a - b = 13
Now, we can solve this system of equations. Adding the two equations, we get:
2a = 24
a = 12
Substituting the value of a into one of the equations, we find:
12 - b = 13
b = -1
Therefore, the values of a and b are 12 and -1 respectively.
For more such questions on polynomial
https://brainly.com/question/1496352
#SPJ8
Hello random community i have a question to ask what is 7/8 - 3/4
Answers
Answer: 1/8
Step-by-step explanation:
First make the bottom half the same:
3/4*2/2=6/8
We don’t need to change the first portion since they have a common factor
7/8-6/8=1/8
c) I use the 4 triangles to make a trapezium. What is the area of the trapezium?
Answers
Answer:
1/2=10
Step-by-step explanation:
it depends upon the area of the triwngle
what are the coordinates of the point that corresponds to -5pi/4 on the unit circle
Answers
The coordinates of the point that corresponds to -5π/4 on the unit circle is (-1/√2, 1/√2).
Given that,
We have to find the coordinates of the point that corresponds to -5π/4 on the unit circle.
We know that any point on the unit circle can be defined as,
(cos θ, sin θ)
where θ is the angle formed with the X axis.
-5π/4 will be the point the corresponds to -225°.
Cos(-5π/4) = cos (5π/4)
= cos (π + π/4)
= -cos (π/4)
= -1/√2
sin (-5π/4) = -sin (5π/4)
= -sin (π + π/4)
= sin (π/4)
= 1/√2
Hence the coordinate of the unit circle is (-1/√2, 1/√2).
Learn more about Unit Circle here :
https://brainly.com/question/8676507
#SPJ1
PLEASE HELP
The table of values represents an exponential function.
What is the y-coordinate of -3f(x-1) when x = 0
Enter your answer in the box.
SEE PHOTO

Answers
The y-coordinate of -3f(x-1) when x = 0 is -63
What is the y-coordinate of -3f(x-1) when x = 0From the question, we have the following parameters that can be used in our computation:
The table of values
So, we have
-3f(x - 1)
When x = 0, we have
y = -3f(0 - 1)
This gives
y = -3f(-1)
From the table, we have
y = -3 * 21
Evaluate
y = -63
Hence, the y-coordinate is -63
Read more about exponential function at
https://brainly.com/question/2456547
#SPJ1
what is 999.09344471 rounded to the nearest square kilometer?
Answers
The nearest kilometers to 999.09344471 km is 1000 km.
Given value is 999.09344471 Km.
We have to calculate the round off value to the nearest kilometers. we know that after the decimal if the value of tenth place is 5 or bigger than 5 then we add 1 to the tens place digit, this is the fundamental rule of rounding off.
Now on following this rule from the very right hand side up to the tenth place digit we come to the conclusion that only the value after the decimal (934) is to be rounded off which is (900).
So 999.09344471 km is finally becomes 999.900 km after rounding of to nearest hundredth value.
Again rounding off 999.900 km to nearest km so it becomes 1000 km.
The nearest kilometers to 999.09344471 km is 1000 km.
For more details on round off follow the link:
brainly.com/question/1093198
Use implicit differentiation to find an equation of the tangent line to the curve at the given points. (x2 + y2)2 = 3x2y − y3;
(a) (0, −1),
(b) (−1/2, 1/2)
Answers
Answer:
a.\(y+1=0\)
b.\(2x+4y=1\)
Step-by-step explanation:
We are given that
\((x^2+y^2)^2=3x^2y-y^3\)
a.(0,-1)
Differentiate w.r.t x
\(2(x^2+y^2)(2x+2yy')=6xy+3x^2y'-3y^2y'\).....(1)
Substitute x=0 and y=-1 in equation (1)
\(2(0+1)(-2y')=-3y'\)
\(-4y'+3y'=0\)
\(-y'=0\)
\(y'=0\)
\(m=y'=0\)
Point-slope form:
\(y-y_0=m(x-x_0)\)
Using the formula
\(y+1=0\)
This is required equation of tangent line to the given curve at point (0,-1).
b.(-1/2,1/2)
Substitute the value in equation (1)
\(2(1/4+1/4)(-1+y')=6(-1/2)(1/2)+3(1/4)y'-3(1/4)y'\)
\(2(2/4)(-1+y')=-3/2+3/4y'-3/4y'\)
\(-1+y'=-3/2\)
\(y'=-3/2+1=\frac{-3+2}{2}=-\frac{1}{2}\)
\(m=y'=-1/2\)
Again using point-slope formula
\(y-1/2=-1/2(x+1/2)\)
\(\frac{2y-1}{2}=-\frac{1}{4}(2x+1)\)
\(2y-1=-\frac{1}{2}(2x+1)\)
\(4y-2=-2x-1\)
\(2x+4y=2-1\)
\(2x+4y=1\)
A bank manager wants to encourage new customers to open accounts with principals of at least $. He decides to make a poster advertising a simple interest rate of %. What must the principal be if the bank manager also wants to advertise that one can earn $ the first month? Can the poster correctly say, "Open an account of $ and earn at least $ interest in 1 month!"? Can the poster correctly say, "Open an account of $ and earn at least $ interest in !"?
Answers
The principal must have a value of $2,500. if the bank manager also wants to advertise that one can earn $10 the first month.
Hence, with a principal of $3,350, it is possible for the poster to correctly say the statement, as the needed principal is less than $3,350.
How to obtain the necessary principal?As the problem states, simple interest is used, meaning that there is a single compounding per period.
The equation that gives the interest accrued after t years is given as follows:
I(t) = Prt.
The parameters of the interest equation are given as follows:
P is the value of the initial deposit.r is the interest rate, as a decimal.The values of the measures in this problem are given as follows:
I(1/12) = 10.t = 1/12.r = 0.048.Hence the principal is obtained solving the equation as follows:
10 = P x 1/12 x 0.048
0.004P = 10
P = 10/0.004
P = $2,500.
Missing InformationThe problem is of:
"A bank manager wants to encourage new customers to open accounts with principals of at least $3,500. He decides to make a poster advertising a simple interest rate of 4.8%. What must the principal be if the bank manager also wants to advertise that one can earn $10 the first month? Can the poster correctly say, "Open an account of $3,500 and earn at least $10 interest in 1 month!"?"
More can be learned about simple interest at https://brainly.com/question/20690803
#SPJ1
2 3/4 of 500grams in step by step calculator
Answers
Answer:
To calculate 2 3/4 of 500 grams, follow these steps:
1. Convert the mixed number to an improper fraction:
2 3/4 = (2 x 4 + 3)/4 = 11/4
2. Multiply the improper fraction by 500:
11/4 x 500 = (11 x 500)/4 = 2,750/4
3. Simplify the fraction by dividing the numerator and denominator by their greatest common factor, which is 2:
2,750/4 = (2 x 1,375)/(2 x 2) = 1,375/2
Therefore, 2 3/4 of 500 grams is equal to 1,375/2 grams or 687.5 grams.
Step-by-step explanation:
what is the area of the regular polygon shown below?

Answers
Because the apothem will always be half of the length of one side. The length of one side is 28 in.
The formula for the area is:
Area = (number of sides × length of one side × apothem)/2
Working out:
A = (7 times 28 times 14) divided by 2 = 1372 in. squared
Hope this helps!
Please give Brainliest!
Find the unit rate (constant of proportionality) of the distance traveled.
Number of hours
0.25 1.5 2.5 3
Distance traveled (km) 3 18 30 36
Answers
Answer:
12.
Step-by-step explanation:
if to re-write the given condition, then
\(\frac{3}{0.25} =\frac{18}{1.5} =\frac{30}{2.5} =\frac{36}{3} ;\)
it is clear, the required constant is 12 (12 per hour).
ppppppppppppppppppppppppppppppppppppiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiipppppppppppppppppppppppppppppppppppppppppppppppeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeemmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeee
Answers
NEED ANWSER ASAP PLS
a horizontal translation only
a horizontal translation and a 180° rotation
a horizontal translation and a glide reflection
a horizontal translation and a reflection across a vertical line

Answers
The transformations that map the strip pattern onto itself is a horizontal translation, a reflection across a vertical line, a reflection across a horizontal line, a glide reflection, and a 180°. Option A is the correct option.
Here, we have,
the conditions for mapping the strip transformation pattern onto itself:
The strip pattern can be mapped onto itself in two different ways.
The first way is to translate the strip pattern horizontally and then rotate it by 180° degrees.
The second way is to reflect the strip pattern across a vertical line.
Hence, the transformations that map the strip pattern onto itself can be achieved through a horizontal translation, a reflection across a vertical line, a reflection across a horizontal line, a glide reflection, and a 180°.
Learn more about transformations map on
brainly.com/question/7721186
#SPJ1
complete question:
Which transformations map the strip pattern onto itself?
a horizontal translation, a reflection across a vertical line, a reflection across a horizontal line, a glide reflection, and a 180°
a horizontal translation only
a horizontal translation, a reflection across a horizontal line, and a glide reflection only
a horizontal translation and a 180° rotation only
A basketball player averages 12,5 points per game. There are 24 games in a season. At this rate, how many points
would the player score in an entire season?
In the entire season, the basketball player would score
points.
✓ Done
Intro
15 of 15
Answers
Answer:
12.5 x 24=300
Step-by-step explanation:
The overhead reach distances of adult females are normally distributed with a mean of 197.5 cm197.5 cm and a standard deviation of 8.3 cm8.3 cm. a. Find the probability that an individual distance is greater than 210.90210.90 cm. b. Find the probability that the mean for 1515 randomly selected distances is greater than 196.00 cm.196.00 cm. c. Why can the normal distribution be used in part (b), even though the sample size does not exceed 30?
Answers
Answer:
a) 5.37% probability that an individual distance is greater than 210.9 cm
b) 75.80% probability that the mean for 15 randomly selected distances is greater than 196.00 cm.
c) Because the underlying distribution is normal. We only have to verify the sample size if the underlying population is not normal.
Step-by-step explanation:
To solve this question, we need to understand the normal probability distribution and the central limit theorem.
Normal probability distribution
Problems of normally distributed samples are solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the zscore of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
Central Limit Theorem
The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean \(\mu\) and standard deviation \(\sigma\), the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean \(\mu\) and standard deviation \(s = \frac{\sigma}{\sqrt{n}}\).
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
In this question, we have that:
\(\mu = 197.5, \sigma = 8.3\)
a. Find the probability that an individual distance is greater than 210.9 cm
This is 1 subtracted by the pvalue of Z when X = 210.9. So
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{210.9 - 197.5}{8.3}\)
\(Z = 1.61\)
\(Z = 1.61\) has a pvalue of 0.9463.
1 - 0.9463 = 0.0537
5.37% probability that an individual distance is greater than 210.9 cm.
b. Find the probability that the mean for 15 randomly selected distances is greater than 196.00 cm.
Now \(n = 15, s = \frac{8.3}{\sqrt{15}} = 2.14\)
This probability is 1 subtracted by the pvalue of Z when X = 196. Then
\(Z = \frac{X - \mu}{\sigma}\)
By the Central Limit Theorem
\(Z = \frac{X - \mu}{s}\)
\(Z = \frac{196 - 197.5}{2.14}\)
\(Z = -0.7\)
\(Z = -0.7\) has a pvalue of 0.2420.
1 - 0.2420 = 0.7580
75.80% probability that the mean for 15 randomly selected distances is greater than 196.00 cm.
c. Why can the normal distribution be used in part (b), even though the sample size does not exceed 30?
The underlying distribution(overhead reach distances of adult females) is normal, which means that the sample size requirement(being at least 30) does not apply.
Which expression is equivalent to 5(4x + 12) + 3x + 2?
A. 85x
B. 23x + 62
C. 23x + 14
D. 20x + 60
Answers
\(\boxed{\sf B.\,23x + 62}.\)
Step-by-step explanation:Let's simplify this expression1. Write the expression.\(\sf 5(4x + 12) + 3x + 2\)
2. Aplly the distributive property of multiplication to solve the parenthesis (check the attached image).\(\sf (5)(4x)+(5)(12) + 3x + 2\\ \\20x+60 + 3x + 2\)
3. Add up the like terms.\(\sf 20x+ 3x + 2+60 \\ \\\boxed{\sf 23x + 62} \Longrightarrow Final\,answer.\)
-------------------------------------------------------------------------------------------------------
Solving equations is a process that involves a lot mathematical simplification. That's why I suggest you take a look at these answers to learn more about simplifying:
brainly.com/question/30596312
brainly.com/question/28282032
brainly.com/question/28306861
brainly.com/question/28285756
brainly.com/question/28306307
brainly.com/question/30015231
brainly.com/question/29888440
brainly.com/question/31757124

Help Asap
One tube of paint covers 1,400 square inches of ramp. Based on this, how many tubes of paint will be needed to paint the ramp
My answer from the answer above is 3,672 sq in.
Answers
Answer:
3
Step-by-step explanation:
The number of tubes can be found from an inequality that relates the number of square inches that can be painted to the number of square inches that must be painted.
Let t represent the number of tubes.
1400t ≥ 3672 . . . . . the number of tubes that will paint at least 3672 in²
t > 2.623 . . . . . divide by 1400
If only whole numbers of tubes are available, then ...
3 tubes are needed to paint the ramp.
Answer:
Step-by-step explanation:
The number of tubes can be found from an inequality that relates the number of square inches that can be painted to the number of square inches that must be painted.
Let t represent the number of tubes.
1400t ≥ 3672 . . . . . the number of tubes that will paint at least 3672 in²
t > 2.623 . . . . . divide by 1400
If only whole numbers of tubes a
prove that -
\( \sin(3x) + \sin(2x) - \sin(x) = 4 \sin(x ) \cos( \frac{x}{2} ) \cos( \frac{3x}{2} ) \\ \)
thankyou ~
kindly move the screen to see the complete question ~
Answers
Let x = 2y. Then we want to show
sin(6y) + sin(4y) - sin(2y) = 4 sin(2y) cos(y) cos(3y)
Recall the angle sum identities,
sin(x ± y) = sin(x) cos(y) ± cos(x) sin(y)
cos(x ± y) = cos(x) cos(y) ∓ sin(x) sin(y)
which lets us write
sin(6y) = sin(4y + 2y) = sin(4y) cos(2y) + cos(4y) sin(2y)
sin(4y) = sin(2y + 2y) = 2 sin(2y) cos(2y)
cos(4y) = cos(2y + 2y) = cos²(2y) - sin²(2y)
Ultimately, we use these identities to rewrite the left side as
sin(6y) + sin(4y) - sin(2y)
= 2 (sin(4y) cos(2y) + cos(4y) sin(2y)) + 2 sin(2y) cos(2y) - sin(2y)
= 2 sin(2y) cos²(2y) + (cos²(2y) - sin²(2y)) sin(2y) + 2 sin(2y) cos(2y) - sin(2y)
Notice the underlined common factor of sin(2y). If we remove this from both sides of the identity we want to prove, then it remains to show that
2 cos²(2y) + (cos²(2y) - sin²(2y)) + 2 cos(2y) - 1 = 4 cos(y) cos(3y)
or
3 cos²(2y) - sin²(2y) + 2 cos(2y) - 1 = 4 cos(y) cos(3y)
Recall the Pythagorean identity,
cos²(x) + sin²(x) = 1
which lets us write
3 cos²(2y) - sin²(2y) + 2 cos(2y) - 1
= 3 cos²(2y) - (1 - cos²(2y)) + 2 cos(2y) - 1
= 4 cos²(2y) + 2 cos(2y) - 2
= 2 (2 cos²(2y) + cos(2y) - 1)
= 2 (2 cos(2y) - 1) (cos(2y) + 1)
Recall the half-angle identity for cosine,
cos²(x/2) = 1/2 (1 + cos(x))
which means
cos(2y) + 1 = 2 • 1/2 (1 + cos(2y)) = 2 cos²(y)
and so
2 (2 cos(2y) - 1) (cos(2y) + 1)
= 4 (2 cos(2y) - 1) cos²(y)
= 4 cos(y) (2 cos(2y) - 1) cos(y)
Now notice the underlined factor of 4 cos(y), which also appears in the right side of the identity we want to prove. Eliminate this term and all that's left is to show that
(2 cos(2y) - 1) cos(y) = cos(3y)
which follows from a combination of the identities I mentioned above:
(2 cos(2y) - 1) cos(y)
= 2 cos(2y) cos(y) - cos(y)
= 2 • 1/2 (cos(2y + y) + cos(2y - y)) - cos(y)
= (cos(3y) + cos(y)) - cos(y)
= cos(3y)
as required.
Trigonometric identities involve equations that use the trigonometric functions that are true for all variables in the equation
The identity is given as:
\(\sin(3x) + \sin(2x) - \sin(x) = 4\sin(x)\cos(\frac x2)\cos(\frac{3x}{2})\)
Let x = 2y.
So, we have:
\(\sin(6y) + \sin(4y) - \sin(2y) = 4\sin(2y)\cos(y)\cos(3y)\)
Expand
\(\sin(4y + 2y) + \sin(2y + 2y) - \sin(2y) = 4\sin(2y)\cos(y)\cos(3y)\)
Expand the identities using the angle sum identities,
\(\sin(4y)\cos(2y) + \cos(4y)\sin(2y) + 2\sin(2y)\cos(2y) - \sin(2y) = 4\sin(2y)\cos(y)\cos(3y)\)
Expand cos(4y) and sin(4y)
\(2\sin(2y)\cos^2(2y) + [\cos^2(2y) - \sin^2(2y)]\sin(2y) + 2\sin(2y)\cos(2y) - \sin(2y) = 4\sin(2y)\cos(y)\cos(3y)\)
Factor out sin(2y)
\(\sin(2y)[2\cos^2(2y) + \cos^2(2y) - \sin^2(2y) + 2\cos(2y) - 1] = 4\sin(2y)\cos(y)\cos(3y)\)
Evaluate the like terms
\(\sin(2y)[3\cos^2(2y) - \sin^2(2y) + 2\cos(2y) - 1] = 4\sin(2y)\cos(y)\cos(3y)\)
Substitute
\(\sin^2(2y) = 1 - \cos^2(2y)\)
\(\sin(2y)[3\cos^2(2y) - 1 + \cos^2(2y) + 2\cos(2y) - 1] = 4\sin(2y)\cos(y)\cos(3y)\)
Evaluate the like terms
\(\sin(2y)[4\cos^2(2y) - 1 + 2\cos(2y) - 1] = 4\sin(2y)\cos(y)\cos(3y)\)
\(\sin(2y)[4\cos^2(2y) + 2\cos(2y) - 2] = 4\sin(2y)\cos(y)\cos(3y)\)
Factor out 2
\(2\sin(2y)[2\cos^2(2y) + \cos(2y) - 1] = 4\sin(2y)\cos(y)\cos(3y)\)
Expand
\(2\sin(2y)[2\cos^2(2y) +2\cos(2y) - \cos(2y) - 1] = 4\sin(2y)\cos(y)\cos(3y)\)
Factorize
\(2\sin(2y)[2\cos(2y)( \cos(2y) + 1) -1( \cos(2y) + 1)] = 4\sin(2y)\cos(y)\cos(3y)\)
Factor out cos(2y) + 1
\(2\sin(2y)[( 2\cos(2y) - 1)( \cos(2y) + 1)] = 4\sin(2y)\cos(y)\cos(3y)\)
By half identity, we have:
\(\cos\²(\frac x2) = \frac 12 (1 + \cos(x))\)
Multiply both sides by 2
\(2\cos\²(\frac x2) = (1 + \cos(x))\)
Replace x with 2y
\(2\cos\²(y) = 1 + \cos(2y)\)
So, we have:
\(2\sin(2y)[( 2\cos(2y) - 1)( 2\cos^2(y))] = 4\sin(2y)\cos(y)\cos(3y)\)
\(4\sin(2y)(2 \cos(2y) - 1)(\cos^2(y)) = 4\sin(2y)\cos(y)\cos(3y)\)
Factor out cos(y)
\(4\sin(2y)(\cos(y)(2 \cos(2y) - 1)(\cos(y)) = 4\sin(2y)\cos(y)\cos(3y)\)
Expand
\(4\sin(2y)(\cos(y)(2 \cos(2y)\cos(y) - \cos(y)) = 4\sin(2y)\cos(y)\cos(3y)\)
Using the half identity, we have:
\(4\sin(2y)(\cos(y)(2 * \frac 12 *\cos(2y + y) + \cos(2y - y) - \cos(y)) = 4\sin(2y)\cos(y)\cos(3y)\)
\(4\sin(2y)(\cos(y)(\cos(3y) + \cos(y) - \cos(y)) = 4\sin(2y)\cos(y)\cos(3y)\)
\(4\sin(2y)\cos(y)\cos(3y) = 4\sin(2y)\cos(y)\cos(3y)\)
Recall that:
x = 2y
So, we have:
\(4\sin(x)\cos(\frac x2)\cos(\frac {3x}2) = 4\sin(x)\cos(\frac x2)\cos(\frac {3x}2)\)
Both sides of the equations are the same.
Hence, the identity \(\sin(3x) + \sin(2x) - \sin(x) = 4\sin(x)\cos(\frac x2)\cos(\frac{3x}{2})\) has been proved
Read more about trigonometry identity at:
https://brainly.com/question/7331447