what is 4 multiplied by 4

a) The value of z corresponding to an area of 0.1210 can be found using statistical tables or a statistical calculator.

b) Similarly, the value of z corresponding to an area of 0.9898 can be obtained using statistical tables or a statistical calculator.

c) To find the value of z at the 45th percentile, we can use the standard normal distribution table or a statistical calculator.

a) To find the value of z corresponding to an area of 0.1210, you can use a standard normal distribution table or a statistical calculator. By looking up the area of 0.1210 in the table, you can determine the corresponding z-value. For example, if you find that the z-value for an area of 0.1210 is -1.15, then -1.15 is the value of z corresponding to the given area.

b) Similarly, to find the value of z corresponding to an area of 0.9898, you can refer to a standard normal distribution table or use a statistical calculator. Find the z-value that corresponds to the area of 0.9898. For instance, if the z-value for an area of 0.9898 is 2.32, then 2.32 is the value of z corresponding to the given area.

c) To find the value of z at the 45th percentile, you can use a standard normal distribution table or a statistical calculator. The 45th percentile corresponds to an area of 0.4500. By finding the z-value for an area of 0.4500, you can determine the value of z at the 45th percentile. For example, if the z-value for an area of 0.4500 is 0.125, then 0.125 is the value of z at the 45th percentile.

To learn more about  area Click Here:  brainly.com/question/22469440

#SPJ11

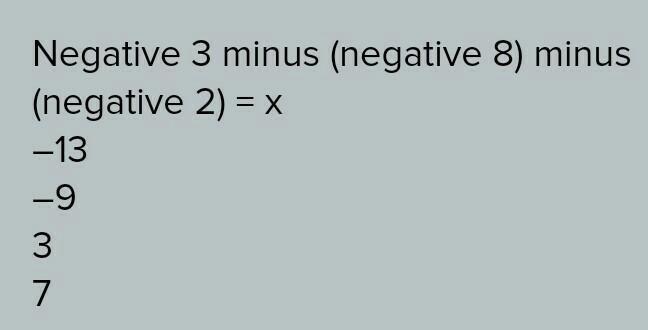
Answer:

6 cans of paint.

Step-by-step explanation:

3/4 of a can of paint is enough to paint 1/8 of his wall. He needs to paint 1 wall. So, what does 1/8 have to be multiplied to equal 1? 8.

1/8*8=1

This means that Jason needs 3/4*8=6 cans of paint to paint the entire wall.

Answer:

3 wholes 2/5

I hope this helps you!

On solving the provided question, we can say that in the quadrilateral BD = 11, BC = 8, DC = 8 and perimeter of ABCD is = 38

A quadrilateral is a four-sided polygon in geometry that has four edges and four corners. The word is a derivative of the Latin words quadri and latus (meaning "side"). Having four sides, four vertices, and four corners, a rectangle is a two-dimensional form. Concave and convex come in primarily two varieties. Additionally, there are several subclasses of convex quadrilaterals, including trapezoids, parallelograms, rectangles, rhombuses, and squares. Four straight sides make up a rectangle, which is a two-dimensional form. There are several different types of quadrilaterals, including parallelograms, trapezoids, rectangles, kites, squares, and rhombuses.

in the quadrilateral

BD = 11 ( equal angle have equal sides)

BC = 8

DC = 8

perimeter of ABCD is = 38

To know more about quadrilateral visit:

https://brainly.com/question/29934291

#SPJ1

Answer:

0.4 x 10^-1

Step-by-step explanation:

4 x 10^0

=> 4

=> 0.4 x 10^-1

Answer:

Graphing the equation we have;

Explanation:

Given the equation;

the slope of the line can be derived by expressing the equation in slope-intercept form;

So, the slope and y-intercept are;

to graph the equation, let us find the x-intercept;

Graphing the equation we have;

Other points on the graph includes;

Answer:

f(x) = (x - 2)² + 2

Step-by-step explanation:

The vertex form of the quadratic function is:

f(x) = a(x - h)² + k

where:

(h, k) = vertex

The axis of symmetry is the imaginary vertical line where x = h

a = determines whether the graph opens up or down, and how wide or narrow the graph will be.

h = determines the horizontal translation of the parabola.

k = determines the vertical translation of the graph.

Given the vertex occurring at point (2, 2), along with one of the points on the graph, (4, 6):

Substitute these values into the vertex form of the quadratic function:

f(x) = a(x - h)² + k

6 = a(4 - 2)² + 2

6 = a(2)² + 2

6 = 4a + 2

Subtract 2 from both sides:

6 - 2 = 4a + 2 - 2

4 = 4a

Divide both sides by 4:

4/4 = 4a/4

1 = a

Therefore, the quadratic function in vertex form is: f(x) = (x - 2)² + 2

\({\dashrightarrow\sf{5x + 3 = \dfrac{4}{3} \bigg(1 + x \bigg)}}\)

\({\dashrightarrow\sf{3 \bigg(5x + 3 \bigg)= 4\bigg(1 + x \bigg)}}\)

\({\dashrightarrow\sf{\bigg(5x \times 3 + 3 \times 3 \bigg)= \bigg(1 \times 4 + x \times 4 \bigg)}}\)

\({\dashrightarrow\sf{\bigg(15x + 9 \bigg)= \bigg(4 + 4x\bigg)}}\)

\({\dashrightarrow\sf{15x - 4x =4 - 9 }}\)

\({\dashrightarrow\sf{11x =4 - 9 }}\)

\({\dashrightarrow\sf{11x = - 5 }}\)

\({\dashrightarrow\sf{x = - \dfrac{5}{11}}}\)

\(\bigstar{\underline{\boxed{\sf{\red{x = - \dfrac{5}{11}}}}}}\)

∴ The value of x is -5/11.

\(\begin{gathered}\end{gathered}\)

\({\dashrightarrow\sf{5x + 3 = \dfrac{4}{3} \bigg(1 + x \bigg)}}\)

\({\dashrightarrow\sf{ \bigg(\left\{5 \times - \dfrac{5}{11} \right\} + 3 \bigg)= \dfrac{4}{3} \bigg(1 + \left\{ - \dfrac{5}{10}\right\}\bigg)}}\)

\({\dashrightarrow\sf{ \bigg(\left\{- \dfrac{25}{11} \right\} + 3 \bigg)= \dfrac{4}{3} \bigg(1 + \left\{ - \dfrac{5}{11}\right\}\bigg)}}\)

\({\dashrightarrow\sf{ \bigg( \dfrac{ - ( 25 )+ (3 \times 11)}{11} \bigg)= \dfrac{4}{3} \bigg( \dfrac{(1 \times 11) - (5 \times 1)}{11}\bigg)}}\)

\({\dashrightarrow\sf{ \bigg( \dfrac{ - 25+ 33}{11} \bigg)= \dfrac{4}{3} \bigg( \dfrac{11 - 5}{11}\bigg)}}\)

\({\dashrightarrow\sf{ \bigg( \dfrac{8}{11} \bigg)= \dfrac{4}{3} \bigg( \dfrac{6}{11}\bigg)}}\)

\({\dashrightarrow\sf{ \bigg( \dfrac{8}{11} \bigg)= \bigg(\dfrac{4}{3} \times \dfrac{6}{11}\bigg)}}\)

\({\dashrightarrow\sf{ \bigg( \dfrac{8}{11} \bigg)= \bigg(\dfrac{4 \times 6}{3 \times 11}\bigg)}}\)

\({\dashrightarrow\sf{ \bigg( \dfrac{8}{11} \bigg)= \bigg(\dfrac{24}{33}\bigg)}}\)

\({\dashrightarrow\sf{ \bigg( \dfrac{8}{11} \bigg)= \bigg(\cancel{\dfrac{24}{33}}\bigg)}}\)

\({\dashrightarrow\sf{ \bigg( \dfrac{8}{11} \bigg)= \bigg({\dfrac{8}{11}}\bigg)}}\)

\(\bigstar{\underline{\boxed{\sf{\red{LHS = RHS}}}}}\)

∴ Hence Verified !

Answer:

\(x = - \frac{5}{11} \\ \)

Step-by-step explanation:

\(5x + 3 = \frac{4}{3} (1 + x) \\ 5x + 3 = \frac{4}{3} + \frac{4x}{3} \\ 5x - \frac{4x}{3} = \frac{4}{3} - 3 \\ \frac{3(5x) - 4x}{3} = \frac{4 - 3(3)}{3} \\ \frac{15x - 4x}{3} = \frac{4 - 9}{3} \\ \frac{11x}{3} = - \frac{5}{3} \\ 11x = - \frac{5}{3} \times 3 \\ 11x = - 5 \\ x = - \frac{5}{11} \\ \)

Answer:So for an isosceles right triangle with side length a , the hypotenuse has a length of a√2 . Similarly, if the hypotenuse of an isosceles right triangle has length of a , the legs have a length of a√2ora√22 each

Step-by-step explanation:

An isosceles triangle is a special triangle due to the values of its angles. These triangles are referred to as triangles and their side lengths follow a specific pattern that states that one can calculate the length of the legs of an isoceles triangle by dividing the length of the hypotenuse by the square root of 2.

FOR EXAMPLE What is the length of the legs of an isosceles right triangle if the hypotenuse is 8 units?

2 Answers By Expert Tutors. For an isoceles right trangle, the legs each have length x and the hypotenuse has length x √2. Therefore, since the hypotenuse has length 8√2, the legs must each be of length 8.

The completed two column table in the question showing that the measure of the angle m∠GKB = 120° can be presented as follows;

Statement \({}\)                                                Reason

\(\overline{AB}\) || \(\overline{EF}\)         \({}\)                                          Given

m∠ELJ = 120°

m∠ELJ + m∠ELK = 180°     \({}\)                        Linear pair Postulate

m∠BKL + m∠GKB = 180°   \({}\)                        Linear pair Postulate

m∠ELJ + m∠ELK = mBKL + m∠GKB  \({}\)      Transitive property

∠ELK ≅ ∠BKL                         \({}\)                   1. Alternate Interior Angles

m∠ELK = m∠BKL \({}\)                                      2. Definition of congruent angles

m∠ELJ + m∠ELK = m∠ELK + m∠GKB\({}\)      Substitution property

m∠ELJ = m∠GKB\({}\)                                      Subtraction property

m∠GKB = m∠ELJ \({}\)                                     Symmetric property

m∠GKB = 120° \({}\)                                          Substitution

An angle is the figure formed at the point of intersection of two rays that have the same starting point. The parts of an angle includes; The vertex, which is the point of intersection of the rays, and the sides or arms of the angle, which are the two rays forming the angle.

The details of the the statements that completes the above table used to prove the measure of the angle m∠GKB = 120° are as follows;

Alternate interior angles theorem

The alternate interior angles theorem states that the alternate interior angle formed by the two parallel lines and their shared transversal are congruent.

Definition of congruent angles

Congruent angles are angles that have the same measure.

Learn more alternate interior angles here: https://brainly.com/question/20344743

#SPJ4

Answer:

0.20

Step-by-step explanation:

Answer:

Step-by-step explanation:In geometry, pairs of angles can relate to each other in several ways. Some examples are complementary angles, supplementary angles, vertical angles, alternate interior angles, alternate exterior angles, corresponding angles and adjacent angles.

The answer of the given question based on the function is ,  the domain of f(g(x)) is all real numbers except x = 1.

A function, in mathematics, is a relationship or mapping between a set of inputs, called the domain, and a set of outputs, called the codomain or range. It assigns a unique output value to each input value.

Functions are often denoted by a symbol, such as f, and written as f(x), where x represents the input variable.

Here are some key aspects of functions:

Domain: The domain of a function is the set of all possible input values for which the function is defined. It specifies the valid inputs for the function.

Codomain/Range: The codomain or range of a function is the set of all possible output values that the function can produce.

Function Notation: Functions are typically represented using functional notation, such as f(x), where the function name (f) is followed by the input variable (x).

Mapping: A function can be seen as a mapping that relates each input value to a unique output value.

It describes how elements of the domain are transformed or associated with elements of the range.

To find the domain of the composition f(g(x)), we need to consider the domains of both f(x) and g(x).

The function f(x) = (x - 9) / (1) is defined for all real numbers except x = 1, since division by zero is undefined.

The function g(x) = (x⁴ + 5) after performing the given transformations: shift upward 10 units and shift 83 units to the right can be written as g(x) = (x - 83)⁴ + 15.

Now, we need to find the domain of f(g(x)). Since both f(x) and g(x) are defined for all real numbers except x = 1, the domain of the composition f(g(x)) is also all real numbers except x = 1.

Therefore, the domain of f(g(x)) is all real numbers except x = 1.

To know more about Function visit:

https://brainly.in/question/222093

#SPJ11

The factored form of the polynomial P(x) = x³ + 2x² + 4x + 8 is P(x) = (x + 1)(x² + x + 7). The quadratic factor x^2 + x + 7 cannot be further factored into linear factors with real coefficients.

To factor the polynomial P(x) = x³ + 2x² + 4x + 8, we can look for potential roots by applying synthetic division or by using synthetic substitution. In this case, we can start by trying small integer values as possible roots, such as ±1, ±2, ±4, and ±8, using the Rational Root Theorem.

By synthetic substitution, we find that -1 is a root of the polynomial. Dividing P(x) by (x + 1) using long division or synthetic division, we get:

P(x) = (x + 1)(x² + x + 7)

Now, we need to factor the quadratic expression x² + x + 7. However, upon factoring this quadratic expression, we find that it cannot be factored further into linear factors with real coefficients. Therefore, the factored form of P(x) is:

P(x) = (x + 1)(x² + x + 7)

Please note that the quadratic factor x² + x + 7 does not have any real roots. Therefore, the complete factored form of P(x) is as given above.

To know more about polynomial refer here:

https://brainly.com/question/11536910#

#SPJ11

please make me as brainliest

Answer:

A

Step-by-step explanation:

Answer:

To find the perimeter of a polygon, we add up the lengths of all the sides. In this case, we have a quadrilateral with sides of length y+8, y+7, y+7, and y+8.

Perimeter = (y+8) + (y+7) + (y+7) + (y+8)

Simplifying by combining like terms, we get:

Perimeter = 4y + 30

Therefore, the perimeter of the quadrilateral is 4y + 30.

Answer:

4y + 30

Step-by-step explanation:

To find:-

Answer:-

Perimeter is simply the sum of all sides of any figure. Since here it is a quadrilateral, perimeter would be the sum of all four sides of it .

The four sides given to us are , y+7 , y+8 , y+7 and y+8. We can add them to find out the perimeter as ,

Perimeter = y+7 + y+8 + y+7 + y+8

Perimeter = 4y + 30

Hence the perimeter of the given figure is 4y+30 .

Answer:

49th term = 225

Step-by-step explanation:

The following sequence: -15, -10, -5, 0, -5... is an example of an arithmetic progression.

An arithmetic progression or AP for short, is a sequence in which the difference between successive terms is constant. This difference is known as the common difference, and can be found by subtracting a term by its preceding term.

The general formula, for the nth term of an arithmetic progression, is thus:

Tn = a + (n - 1)d, where a = first term, and d = common difference.

In the sequence: -15, -10, -5, 0, 5...,

a = -15, and d = -10--15 = 5

T49 = -15 + (49 - 1)5 = 225

∴ 49th term = 225

The probability that Blaine earns more than $10,100 in 50 days is approximately:

P(X > $10,100) ≈ 1 - 0.7136 ≈ 0.2864 or 28.64%.

To calculate the probability that Blaine earns more than $10,100 after 50 days, we need to use the Central Limit Theorem, assuming that Blaine's daily earnings follow a normal distribution.

The Central Limit Theorem states that the sum or average of a large number of independent and identically distributed random variables tends to follow a normal distribution, regardless of the shape of the original distribution.

Given that Blaine's average earnings per day is $200 with a standard deviation of $25, we can calculate the mean and standard deviation for the sum of his earnings over 50 days:

Mean of 50-day earnings = 50 * $200 = $10,000

Standard deviation of 50-day earnings = √(50) * $25 ≈ $176.78

Now, we want to find the probability that Blaine earns more than $10,100 in 50 days. We can convert this into a standard normal distribution by standardizing the value using the z-score formula:

z = (x - μ) / σ

Where:

x is the value we want to standardize (in this case, $10,100)

μ is the mean of the distribution (in this case, $10,000)

σ is the standard deviation of the distribution (in this case, approximately $176.78)

z = ($10,100 - $10,000) / $176.78 ≈ 0.564

Next, we can use a standard normal distribution table or a calculator to find the probability associated with the z-score of 0.564. The probability of earning more than $10,100 can be calculated as:

P(X > $10,100) = 1 - P(X ≤ $10,100)

= 1 - P(Z ≤ 0.564)

Using a standard normal distribution table or a calculator, we can find that P(Z ≤ 0.564) is approximately 0.7136.

Therefore, the probability that Blaine earns more than $10,100 in 50 days is approximately:

P(X > $10,100) ≈ 1 - 0.7136 ≈ 0.2864 or 28.64%.

To know more about probability refer here:

https://brainly.com/question/32004014

#SPJ11

The expression is simplified to give 2(9x + 2√3x - 5)

First, we need to know that surds are mathematical forms that can no longer be simplified to smaller forms

From the information given, we have that;

(2√3x - 2)(3√3x + 5)

expand the bracket, we get;

6√9x² + 5(2√3x) - 6√3x - 10

Find the square root factor

6(3x)  + 10√3x - 6√3x - 10

collect the like terms, we have;

18x + 4√3x - 10

Factorize the expression, we have;

2(9x + 2√3x - 5)

Learn more about surds at: https://brainly.com/question/840021

#SPJ1

We estimate that f(125) is approximately 52. Based on the given information, we can use the linear approximation method to estimate f(125).

Since we know f(130) = 67 and f′(130) = 3, we can create the linear approximation function:
L(x) = f(130) + f′(130) * (x - 130)
Now we can estimate f(125) using L(x):
L(125) = 67 + 3 * (125 - 130)
L(125) = 67 - 15 = 52
So, the estimated value of f(125) is approximately 52.

To estimate f(125), we can use the linear approximation formula:
f(125) ≈ f(130) + f′(130) * (125 - 130)
Substituting in the given values, we get:
f(125) ≈ 67 + 3 * (-5) = 52
Therefore, we estimate that f(125) is approximately 52.

Learn more about linear here: brainly.com/question/26139696

#SPJ11

Answer:

1,320 ways

Step-by-step explanation:

Only one person can win first, second and third place. The total number of placers is 12 times 11 times 10.

12 × 11 × 10 = 1320

The probability that a randomly selected person is married is 0.2464 or 24.64%.

To find the probability that a randomly selected person is married, we need to consider the proportion of married individuals among cat owners and non-cat owners, as well as the proportion of the population that falls into each category. Let's denote the event "being a cat owner" as A and the event "being married" as B. We are given the following probabilities: P(A) = 48% = 0.48 (proportion of the population that owns a cat); P(B|A) = 39% = 0.39 (proportion of cat owners who are married); P(B|A') = 11% = 0.11 (proportion of non-cat owners who are married). We can use the law of total probability to calculate the probability of being married: P(B) = P(B|A) * P(A) + P(B|A') * P(A'). P(A') represents the complement of event A, which is the event of not being a cat owner.

Since the complement of owning a cat is not owning a cat, P(A') is equal to 1 - P(A). Substituting the given values: P(B) = 0.39 * 0.48 + 0.11 * (1 - 0.48) = 0.1872 + 0.0592 = 0.2464. Therefore, the probability that a randomly selected person is married is 0.2464 or 24.64%.

To learn more about  probability click here: brainly.com/question/31828911

#SPJ11

No, the line x=1-2t, y=2+5t, z=-3t is not parallel to the plane 2x+y-z=8 as their dot product is not zero.

To determine if the line x = 1 - 2t, y = 2 + 5t, z = -3t is parallel to the plane 2x + y - z = 8, we can find the direction vector of the line and check if it is orthogonal to the normal vector of the plane.

The direction vector of the line is given by the coefficients of t in each component, which is (-2, 5, -3).

The normal vector of the plane is given by the coefficients of x, y, and z in the plane's equation, which is (2, 1, -1).

To check if the direction vector is orthogonal to the normal vector, we can take their dot product and see if it is zero:

(-2, 5, -3) * (2, 1, -1) = -4 + 5 + 3 = 4

Since the dot product is not zero, the direction vector of the line and the normal vector of the plane are not orthogonal, which means the line is not parallel to the plane.

The line x = 1 - 2t, y = 2 + 5t, and z = -3t is not parallel to the plane 2x + y - z = 8, hence the answer is no.

Learn more about dot product here:

https://brainly.com/question/29097076

#SPJ4

8000 pounds is required to produce 200 lb of refined sugar

It takes 200 lb of sugar cane to produce 5 lb of refined sugar

For 1 lb of sugar cane, the number of refined sugar that will be produced is

200= 5

x= 1

cross multiply

5x= 200

x= 200/5

x= 40

The number of pounds of sugar cane required to produce 200 lb of refined sugar is

= 40 × 200

= 8,000

Hence 8000 pounds of sugar cane is required to produce 200 lb of refined sugars

Read more on pounds here

https://brainly.com/question/22851115

#SPJ1

We need to determine a few characteristics of the following linear equation:

The first step we need to take is to isolate the "y" variable on the left side.

Now we need to analyze this function and provide the necessary characteristics.

First is the Domain. The Domain of a function is the group of all numbers that can be used as an input (x), in this case the Domain is the whole Real group.

Second is the Range, which is the group of numbers that can be the output of the function (y), for this case we also have the whole Real group as Range.

Then we need to find the "Zero". Which is the value at which the function crosses the x-axis, to calculate it we must make "y=0" and solve for x.

The zero is equal to 12.

The slope of the function is the number multiplying "x", in this case it is -1/2.

The slope is negative, decrescent.

To find the value of f(8), we need to replace x by 8 and solve for y.

The value of f(8) = 2.

To determine the value of x where f(x) is equal to 5, we need to replace f(x) by 5 and solve for x.

The value of x for which f(x) is equal to 5, is 2.

Now we need to graph the equation, for that we have to use two of the points we found before, we will use (8, 2) and (2,5). We need to mark these points at the coordinate plane and draw a line between them:

Answer:

Step-by-step explanation:

39.06

(x+1) & (x-5) are the factors of given equation.

The given Equation is,

x3- \(3x^{3}\) - 9

Here, If we substitute x =5, in the given equation, then we find

     (5)3 - 3(5)3 - 9*5 -5 = 0

x-5 is factor of given equation to find another factor dividing given equation by x-5

    we will get =(x2+2x+1) after dividing the equation by x - 5

Hence x3- \(3x^{3}\) - 9 =(x2+2x+1) (x-5)

                            =(x+2)2 (x-5)

To learn more about Equation click the link

brainly.com/question/29657983

#SPJ4