What is 6 meters in inches? (solution)
Answers
Answer:
6 meters =
236.22 inches
Answer:
6meters=236.2inches
Step-by-step explanation:
Hope this helps! :)
Related Questions
NEED HELP!
what makes this equation true ?
4 = 36 ÷

Answers
Answer:
it would be 144
Answer:
9
Step-by-step explanation:
A shipping container will be used to transport several 120-kilogram crates across the country by rail. The greatest weight that can be loaded into the container is 27500 kilograms. Other shipments weighing 12400 kilograms have already been loaded into the container. Which inequality can be used to determine x, the greatest number of
120-kilogram crates that can be loaded onto the shipping container?
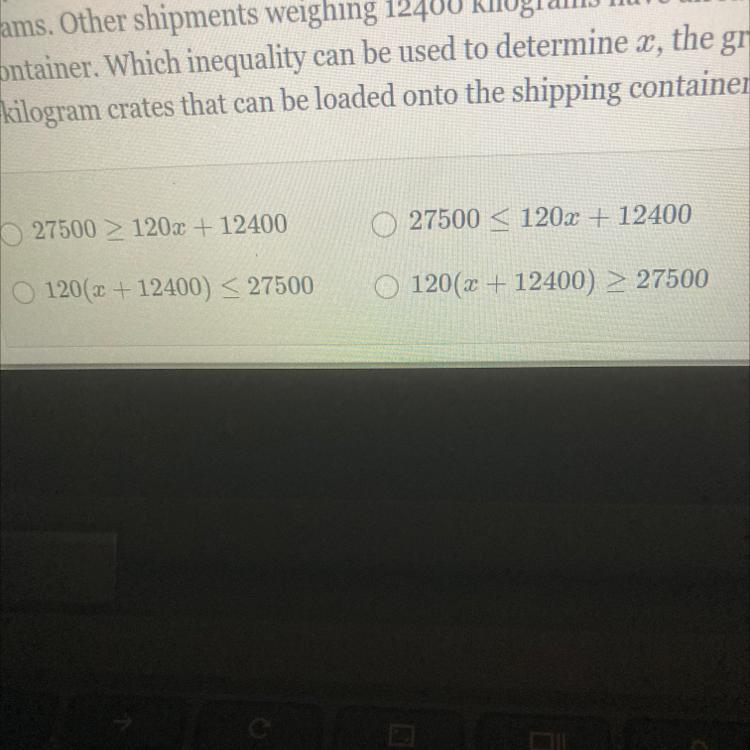
Answers
Inequality can be used to determine x, the greatest number of 120-kilogram crates that can be loaded onto the shipping container is 8000 + 120C <= 27500
What is inequality?An inequality is a relationship that allows us to contrast two or more mathematical expressions.
Knowing that;
Each carton weighs 120 kg.
The container's maximum weight when loaded is 27500 kg.
Weight of the container as it is currently loaded: 8000 kg
Now that we have merged, we have;
Solution
because 8000 grams have already been loaded kilograms
into the container
each crate weighs 120 kilograms.
so 8000 + 120C <= 27500
To learn more about inequality refer to:
https://brainly.com/question/28862943
#SPJ1
Which of the following statements is/are TRUE? Select all that apply.
Split gateways must have exactly two incoming and at least one outgoing sequence flows.
Intermediate events must have at least one incoming and one outgoing sequence flow.
A message flow must connect (an activity or message event of) one pool with (an activity or message event of) a different pool.
Only intermediate catching boundary events can be attached to an activity's border.
Answers
1. True 2. True 3. True 4. False
1. Split gateways must have exactly two incoming and at least one outgoing sequence flows: True.
Split gateways, also known as XOR gateways, are used to create exclusive decision points in a process flow. They require exactly two incoming sequence flows, representing the different paths leading to the decision point. Additionally, there must be at least one outgoing sequence flow, indicating the possible outcomes of the decision.
This ensures that the process flow can continue along one of the paths based on the conditions specified in the gateway.
2. Intermediate events must have at least one incoming and one outgoing sequence flow: True.
Intermediate events occur within the flow of a process and can trigger specific actions or conditions. They must have at least one incoming sequence flow, indicating the event's dependency on a preceding activity or event. Similarly, they must have at least one outgoing sequence flow, showing the subsequent flow of the process after the event occurs.
This ensures that the intermediate event has a clear cause and effect relationship with the surrounding activities.
3. A message flow must connect one pool with a different pool: True.
Message flows represent the exchange of information between pools in a BPMN (Business Process Model and Notation) diagram. Pools typically represent different participants or organizations involved in a process. A message flow connects an activity or message event of one pool to an activity or message event of a different pool, indicating communication or data exchange between them.
This ensures that the process flow accurately represents the interaction between various participants.
4. Only intermediate catching boundary events can be attached to an activity's border: False.
Both intermediate catching and throwing boundary events can be attached to an activity's border. Intermediate catching boundary events are triggered when certain conditions are met during the execution of the activity. They interrupt the normal flow and allow for additional actions to be performed.
On the other hand, intermediate throwing boundary events initiate an external interrupt and can be used to signal an error or exception. Both types of boundary events can enhance the flexibility and exception handling capabilities of an activity.
In summary, the true statements are:
- Split gateways must have exactly two incoming and at least one outgoing sequence flows.
- Intermediate events must have at least one incoming and one outgoing sequence flow.
- A message flow must connect one pool with a different pool.
Learn more about BPMN (Business Process Model and Notation),here
https://brainly.com/question/28465193
#SPJ11
Use the distribution property to rewrite the expression. Then evaluate.
-3(2x-6)
Answers
Answer: -6x+18
Step-by-step explanation:
-3(2x-6)=
-3*2x-(-3*6)= ==> During distribution
-6x-(-18)=-6x+18 ==> After distribution property
Find the perimeter of composite figures

Answers
Answer: 15 ft
Step-by-step explanation:
You basically add all the sides:
3 + 3 + 3 + 3 +3 = 15 ft
And if you have to add 12 ft then the answer should be 27 ft in total.
I hope this helped!
If You Have NO EXPLANATION Don't ANSWER

Answers
Answer:
B. A = 1/2(7)h
Step-by-step explanation:
Formula for area of triangle = 1/2 x base x height
H is the height of the triangle.
7cm is identified as the base of the triangle.
1/2(7)h is also the same thing as 1/2 x 7 x h basically.
Answer:
B
Step-by-step explanation:
The area (A) of a triangle is calculated as
A = \(\frac{1}{2}\) bh ( b is the base and h the perpendicular height )
Here b = 7 and h = h , then
A = \(\frac{1}{2}\) (7) h → B
if i get 20 dollars every 2 weeks for 3 months how much will i have
Answers
Answer:
120
Step-by-step explanation:
3 mons = 12 weeks
$20 every 2 weeks, so average $10 / week
so 12*10 = 120
A jar containing 17 coins (pennies, dimes and quarters) has a total value of $2.06. If you remove 5 pennies, 5 dimes and 5 quarters from the jar, which coins will remain in the jar?
Answers
5 dimes= .50
5 quarters= $1.25
Add those together and get:
1.80
Subtract 1.80 from 2.06
And you’ll get:
.26
Meaning there is a quarter and a penny left.
5 dimes equal $0.50
5 quarters equal $1.25
In total that is $1.80
If you take that away from $2.06 you get $0.26.
You have 2 coins left so you have one quarter and one penny.
What’s next in the sequence
1/3, 7/15, 3/5, 11/15…
Answers
Answer:
The next number in the sequence is 17/15.
Step-by-step explanation:
Factorize the following by splitting the middle term:-
(a) 3x^2 +11x+30
Answers
Answer:
See explanation
Question has been corrected
Step-by-step explanation:
Given:
3x² + 11x + 30
To factorise, multiply the coefficient of x² by 30
= 3 * 30
= 90
Find two numbers that have a product of 90 and a sum of 11
** There are no such two numbers, therefore the question can't be solved using factorization
Correcting the error in the question:
x² + 11x + 30
To factorise, multiply the coefficient of x² by 30
= 1 * 30
= 30
Find two numbers that have a product of 30 and a sum of 11
6 and 5
6 + 5 = 11
6 * 5 = 30
x² + 11x + 30
= x² + 6x + 5x + 30
= x(x + 6) + 5(x + 6)
= (x + 6) (x + 5)
A man walks 10 miles in x hours. How far does he walk in one hour?
Which expression represents this?
10 + x miles
10x miles
miles
Answers
Answer:
10/x represents how far he walks in one hour
Step-by-step explanation:
A quadratic function, f(x) = x2 + bx + 9, is such that there is only one real root. Which of the following are possible values of b?
I. b = 2
II. b = 6
III. b = -6
IV. b = -2
A. I, II, III, and IV
B. I and IV only
C. II and III only
D. I only
Answers
Answer:
C
Step-by-step explanation:
Remember that we can use the discriminant to determine the amount of roots that a quadratic function has.
If the determinant equals 0, then we only have one real root.
Our function is given by:
\(f(x)=x^2+bx+9\)
Then the discriminant will be:
\(\Delta = b^2-4(1)(9)=b^2-36\)
We only have one real root, thus our discriminant must be 0:
\(0=b^2-36\)
Solve for b:
\(b^2=36\)
Thus:
\(b=\pm 6\)
The answer is both II and III.
The final answer, then, is C.
What is the point-slope form of a line that has a slope of 5 and passes through the point 3/4 )? Y 3 5 x 4 )]?
Answers
The point-slope form of the line is y - (3/4) = 5(x - (3/4)).
The point-slope form of a line is written as y - y1 = m(x - x1), where m is the slope of the line and (x1, y1) is a point on the line. To find the point-slope form of a line that has a slope of 5 and passes through the point (3/4, 3/4), we can plug in the values for the slope and the point into the point-slope formula. This gives us y - (3/4) = 5(x - (3/4)). This is the point-slope form of the line.
Learn more about Point-Slope Form here:
https://brainly.com/question/24907633
#SPJ4
set up the integral for the volume of the solid of revolution rotating region between y = sqrt(x) and y = x around x=2
Answers
Plug these into the washer method formula and integrate over the interval [0, 1]:
V =\(\pi * \int[ (2 - x)^2 - (2 - \sqrt(x))^2 ] dx \ from\ x = 0\ to\ x = 1\)
To set up the integral for the volume of the solid of revolution formed by rotating the region between y = sqrt(x) and y = x around the line x = 2, we will use the washer method. The washer method formula for the volume is given by:
V = pi * ∫\([R^2(x) - r^2(x)] dx\)
where V is the volume, R(x) is the outer radius, r(x) is the inner radius, and the integral is taken over the interval where the two functions intersect. In this case, we need to find the interval of intersection first:
\(\sqrt(x) = x\\x = x^2\\x^2 - x = 0\\x(x - 1) = 0\)
So, x = 0 and x = 1 are the points of intersection. Now, we need to find R(x) and r(x) as the distances from the line x = 2 to the respective curves:
R(x) = 2 - x (distance from x = 2 to y = x)
r(x) = 2 - sqrt(x) (distance from x = 2 to y = sqrt(x))
Now, plug these into the washer method formula and integrate over the interval [0, 1]:
V =\(\pi * \int[ (2 - x)^2 - (2 - \sqrt(x))^2 ] dx \ from\ x = 0\ to\ x = 1\)
learn more about washer method
https://brainly.com/question/30637777
#SPJ11
if disposable income is 4,000, consumption is 3,500, government purchases is 1,000, and taxes minus transfers are 800, national saving is equal to: a. 300 b. 500 c. 700 d. 1,000
Answers
The disposable income is 4,000, consumption is 3,500, government purchases is 1,000, and taxes minus transfers are 800, national saving is equal to. Therefore, S = 4,000 - 3,500 - 1,000 = 500.Hence, option b is correct.
National savings (S) can be calculated as: S = Y - C - G, where Y is income, C is consumption, and G is government purchases.
To determine S, we must first calculate Y.Y = C + I + G + NX, where I is investment, and NX is net exports.
The formula for calculating national savings is as follows: National savings (S) = Y - C - G
The following is a numerical representation of the above data:Y = C + I + G + NX = 3,500 + I + 1,000 + NX
Disposable income is 4,000, while taxes minus transfers are 800. Therefore, Y + TR - T = C + S.
Now, let's compute this value.
Substitute the given values in the equation4,000 + TR - 800 - T = 3,500 + S600 - T = S + 3500 - 1000S = 500
Substitute the value of S in the formula:S = Y - C - G
Therefore, S = 4,000 - 3,500 - 1,000 = 500Hence, option b is correct.
Learn more about equation here:
https://brainly.com/question/29657983
#SPJ11
What is the Interior angle of a 30gon?
Answers
Answer:
168°
Step-by-step explanation:
please help me solve this

Answers
Answer:
i actually don't know
Step-by-step explanation:
factor this polynomial completely\(10 {x}^{2} - 11x + 3\)
Answers
Given:
There are given the equation:
\(10x^2-11x+3=0\)Explanation:
According to the question:
we need to find the factor of the given equation:
So,
From the equation:
\(\begin{gathered} 10x^{2}-11x+3=0 \\ 10x^2-6x-5x+3=0 \\ (2x-1)(5x-3)=0 \end{gathered}\)Final answer:
Hence, the factor of the given equation is shown below:
\((2x-1)(5x-3)=0\)find the first four terms of the taylor series for the function 2x about the point a=1. (your answers should include the variable x when appropriate.)
Answers
The first four terms of the Taylor series for the function (2x) about the point (a=1) are (2x + 2x - 2).
What are the initial terms of the Taylor series expansion for (2x) centered at (a=1)?To find the first four terms of the Taylor series for the function (2x) about the point (a = 1), we can use the general formula for the Taylor series expansion:
\(\[f(x) = f(a) + f'(a)(x-a) + \frac{f''(a)}{2!}(x-a)^2 + \frac{f'''(a)}{3!}(x-a)^3 + \ldots\]\)
Let's calculate the first four terms:
Starting with the first term, we substitute
\(\(f(a) = f(1) = 2(1) = 2x\)\)
For the second term, we differentiate (2x) with respect to (x) to get (2), and multiply it by (x-1) to obtain (2(x-1)=2x-2).
\(\(f'(a) = \frac{d}{dx}(2x) = 2\)\)
\(\(f'(a)(x-a) = 2(x-1) = 2x - 2\)\)
Third term: \(\(f''(a) = \frac{d^2}{dx^2}(2x) = 0\)\)
Since the second derivative is zero, the third term is zero.
Fourth term:\(\(f'''(a) = \frac{d^3}{dx^3}(2x) = 0\)\)
Similarly, the fourth term is also zero.
Therefore, the first four terms of the Taylor series for the function (2x) about the point (a = 1) are:
(2x + 2x - 2)
Learn more about taylor series
brainly.com/question/31140778
#SPJ11
The side lengths of a 45-45-90 triangle are in the ratio 1 : 1 : SR2 what is tan 45?
SR= square root
Answers
Answer:
Step-by-step explanation:
tan 45=1/1=1
Tan Theta is one of the trigonometric ratios which is equal to opposite / Adjacent in a triangle, the value of tan45 is 1.
What is the 45-45-90 triangle?The 45-45-90 triangle is also an isosceles triangle, which means its two legs are equal in length.
Tan Theta is one of the trigonometric ratios which is equal to opposite / Adjacent in a triangle.
The side lengths of a 45-45-90 triangle are in the ratio 1: 1: \(\sqrt{2}\).
The value of tan45 is given by the following formula;
\(\rm Tan 45 = \dfrac{Perpendicular}{Base}\\\\Tan45=\dfrac{1}{1}\\\\Tan45=1\)
Hence, the value of tan45 is 1.
Learn more about trigonometry here;
https://brainly.com/question/17016719
#SPJ2
Suppose you draw one card, put it back (and re-shuffle), and then draw another. What is the probability that the cards are of different suits
Answers
The probability that the two cards drawn are of different suits is approximately 0.3744 or 37.44%.
The probability that the first card drawn is of a particular suit (say hearts) is 13/52, because there are 13 hearts in the deck. The probability that the second card drawn is of a different suit (say diamonds) is 39/52, because there are 13 cards in each of the three remaining suits.
So, the probability that the first card is a heart and the second card is a diamond is (13/52) × (39/52) = 507/2704.
Similarly, the probability that the first card is a diamond and the second card is a heart is also (13/52) × (39/52) = 507/2704.
The probability that the two cards are of different suits is the sum of these two probabilities:
(507/2704) + (507/2704) = 1014/2704 ≈ 0.3744
for such more question on probability
https://brainly.com/question/13604758
#SPJ11
Question
Assuming you are drawing from a standard deck of 52 cards with 13 cards in each of the 4 suits (hearts, diamonds, clubs, and spades), the probability that the two cards drawn are of different suits can be calculated as follows:
Answer.::::::::::::::::::::::::

Answers
Answer:
C
Step-by-step explanation:
Answer:
C) There are infinitely many solutions since -5=-5 is a true statement.
Step-by-step explanation:
It took Ruthene 1/4 an hour to run 2 mi. What was her average speed?
Answers
Answer:
8
Step-by-step explanation:
Answer:
8mph
Step-by-step explanation:
Because it took Ruthene 1/4 of an hour or 15 minutes to run two miles, if she were to run for an entire hour she would go 4 times as far, or 8 miles. This means that Ruthene had an average speed of 8mph.
Using graph paper, determine the line described by the given point and slope. Click to show the correct graph below. (0,6) and -1
Answers
Answer:
Can't tell
Step-by-step explanation:
Hear me out. There is no graph hear, so I can't answer. Just letting you know
what quality characteristics can be considered and what control
chart do you suggest for each quality ?characteristic
Answers
The quality characteristics to consider vary depending on the industry and product, and the appropriate control chart for each characteristic also differs.
When evaluating the quality of a product or process, it is important to identify the relevant quality characteristics that need to be monitored. The choice of quality characteristics depends on the nature of the industry and the specific product being manufactured.
For example, in the automotive industry, quality characteristics could include factors like engine performance, safety features, and fuel efficiency. On the other hand, in the food industry, quality characteristics might involve factors such as taste, freshness, and nutritional content.
Once the quality characteristics have been identified, control charts can be employed to monitor and maintain the desired quality levels. Control charts are statistical tools that help detect variations and trends in data over time. Different types of control charts are available, each suited for different types of quality characteristics.
For continuous variables, such as measurements or dimensions, the X-bar and R charts are commonly used. The X-bar chart tracks the average value of a characteristic, while the R chart monitors the range or variation within subgroups. These charts are useful for identifying any shifts or changes in the central tendency or dispersion of the characteristic being measured.
For attribute data, such as the presence or absence of a particular feature, the p-chart or c-chart can be utilized. The p-chart monitors the proportion of nonconforming items in a sample, while the c-chart tracks the count of defects per unit. These control charts help in assessing the stability of the process and identifying any unusual or non-random patterns in the data.
Learn more about control charts
brainly.com/question/32392066
#SPJ11
A model ship is built to a scale of 1:400. If the actual length of the ship is
45 m, the length of the model will be cm. (DO NOT put CM in your
answer, only put an exact number without rounding) *
Answers
Answer:
11.25
Step-by-step explanation:
Hero, we are interested in knowing the length of the model of the ship in cm
Now the ratio of the model to the actual is 1:400
let the length of the model be x
This means that;
1:400 = x: 45
1/400 = x/45
45 * 1 = 400 * x
x = 45/400
x = 0.1125
if we convert this to centimeters, we know that 100 cm equals 1 meter
so 0.1125 m will be 0.1125 * 100 = 11.25
subtract ( – 8r–2)–( – 5r–9)
Answers
Answer:\(-3r+7\)
Step-by-step explanation:
given the equation
\((-8r-2)-(-5r-9)\)
Distribute the negative
\(-8r-2+5r+9\)
Combine like terms
\((-8r+5r)+(-2+9)\)
\((-3r)+(7)=\)
\(-3r+7\)
Hope this helps!
Which of these represents the solution to 3x2+14=−37 ?
Answers
Answer:
± x = i sqrt(17) or x = -i sqrt(17)
Step-by-step explanation:
Solve for x:
3 x^2 + 14 = -37
Subtract 14 from both sides:
3 x^2 = -51
Divide both sides by 3:
x^2 = -17
Take the square root of both sides:
Answer: x = i sqrt(17) or x = -i sqrt(17)
Use the remainder theorem to find P(−3) for P(x)=x 4
+3x 3
−2x−6. Specifically, give the quotient and the remainder for the associated division and the value of P(−3). Quotient =□ Remainder = P(−3)=
Answers
The given polynomial is P(x)=x^4-2x-6. We need to find P(-3) using the remainder theorem and give the quotient, remainder, and P(-3) value = 81.
Given, P(x)=x^4-2x-6
The remainder theorem states that if P(x) is divided by x-a, the remainder is P(a).
Hence, to find P(-3), we divide P(x) by x+3 using the long division method as shown below:
```
x^3 - 3x^2 + 7x - 21
x+3) x^4 - 2x - 6
x^4 + 3x^3
_____________
- 3x^3 - 2x
- 3x^3 - 9x^2
_______________
9x^2 - 2x
9x^2 + 27x
___________
-29x - 6
-29x - 87
_______
81
```
Therefore, the quotient is x^3-3x^2+7x-21, the remainder is 81, and P(-3) = 81.
Hence, the quotient, remainder, and P(-3) value are obtained.
To know more about remainder theorem refer here:
https://brainly.com/question/23007119
#SPJ11
9. If a garden pea has 14 chromosomes before meiosis, how many
chromosomes would exist in each nucleus after meiosis 2? *
O a. 7
O b. 14
O c. 28
O d. 56
Answers
During meiosis, the number of chromosomes in each nucleus is reduced by half. Meiosis consists of two divisions: meiosis I and meiosis II. In meiosis I, the chromosome pairs separate, resulting in two cells with half the number of chromosomes as the original cell. I
n meiosis II, each of these cells further divides, resulting in a total of four cells.
Given that a garden pea has 14 chromosomes before meiosis, after meiosis I, each nucleus would contain 7 chromosomes. Then, in meiosis II, these cells undergo further division, resulting in four cells with the same number of chromosomes as after meiosis I, which is 7 chromosomes each.
Therefore, the answer is (a) 7 chromosomes.
To learn more about meiosis: -brainly.com/question/29383386
#SPJ11