What is 6+4 3/4+(-2.5)= explain your answer
Answers
The value of 6+4 3/4 +(-2.5) is 3 3/10
What is PEDMAS?PEDMAS is an acronym that shows the correct order of operations in mathematical problems. The full meaning of PEDMAS is ;
Parentheses
Exponents
Division
Multiplication
Addition
Subtraction
This order is followed when solving mathematical problems.
Solving 6+4 3/4 +(-2.5)
= 6+ 19/4 - 5/2
= ( 24+19-10)/4
= 33/10
= 3 3/10
Therefore the value of 6+4 3/4 +(-2.5) is 3 3/10
learn more about PEDMAS from
https://brainly.com/question/11421179
#SPJ1
Related Questions
If o=12, find the sample size to estimate the mean with an error of +4 and 95 percent confidence (rounded to the next higher integer).
Multiple Choice
75
35
58
113
URGENT
Answers
We need to round up to the next higher integer, the sample size required to estimate the mean with an error of +4 and 95 Percent confidence is 170.
To find the sample size to estimate the mean with an error of +4 and 95 percent confidence, we need to use the formula:
n = [(z*sigma)/E]^2
Where:
n = sample size
z = z-score for 95% confidence level (which is 1.96)
sigma = standard deviation (unknown in this case)
E = maximum allowable error (which is +4 in this case)
We are given that o=12, which is the population standard deviation. Since we do not have any information about the sample standard deviation, we can use the population standard deviation as an estimate. Therefore, we can substitute o=12 in the above formula to get:
n = [(1.96*12)/4]^2
n = 169.64
Since we need to round up to the next higher integer, the sample size required to estimate the mean with an error of +4 and 95 percent confidence is 170.
To Learn More About Percent
https://brainly.com/question/24877689
SPJ11
For each of the finite geometric series given below, indicate the number of terms in the sum and find the sum. For the value of the sum, enter an expression that gives the exact value, rather than entering an approximation.
3 (0.5)^{5} + 3 (0.5)^{6} + 3 (0.5)^{7} + \cdots + 3 (0.5)^{13}
(1) Number of terms
(2) Value of Sum
Answers
Answer:
Number of term N = 9
Value of Sum = 0.186
Step-by-step explanation:
From the given information:
Number of term N = \(3 (0.5)^{5} + 3 (0.5)^{6} + 3 (0.5)^{7} + \cdots + 3 (0.5)^{13}\)
Number of term N = \(3 (0.5)^{5} + 3 (0.5)^{6} + 3 (0.5)^{7} +3 (0.5)^{8}+3 (0.5)^{9} +3 (0.5)^{10} +3 (0.5)^{11}+3 (0.5)^{12}+ 3 (0.5)^{13}\)
Number of term N = 9
The Value of the sum can be determined by using the expression for geometric series:
\(\sum \limits ^n_{k=m}ar^k =\dfrac{a(r^m-r^{n+1})}{1-r}\)
here;
m = 5
n = 9
r = 0.5
Then:
\(\sum \limits ^n_{k=m}ar^k =\dfrac{3(0.5^5-0.5^{9+1})}{1-0.5}\)
\(\sum \limits ^n_{k=m}ar^k =\dfrac{3(0.03125-0.5^{10})}{0.5}\)
\(\sum \limits ^n_{k=m}ar^k =\dfrac{(0.09375-9.765625*10^{-4})}{0.5}\)
\(\sum \limits ^n_{k=m}ar^k =0.186\)
For the given the geometric series, 3·0.5⁵ + 3·0.5⁶ + 3·0.5⁷ + ...+ 3·(0.5)¹³,
the responses are;
(1) The number of terms are 9
(2) The value of the sum is approximately 0.374
How can the geometric series be evaluated?The given geometric series is presented as follows;
3·0.5⁵ + 3·0.5⁶ + 3·0.5⁷ + ...+ 3·(0.5)¹³
(1) The number of terms in the series = 13 - 4 = 9
Therefore;
The number of terms in the series = 9 terms(2) The value of the sum can be found as follows;
The common ratio, r = 0.5
The sum of the first n terms of a geometric progression is presented as follows;
\(S_n = \mathbf{\dfrac{a \cdot (r^n - 1)}{r - 1}}\)
The sum of the first 4 terms are therefore;
\(S_4 = \dfrac{3 \times (0.5^4 - 1)}{0.5 - 1} = \mathbf{ 5.625}\)
The sum of the first 13 terms is found as follows;
\(S_{13} = \dfrac{3 \times (0.5^{13} - 1)}{0.5 - 1} = \mathbf{ \dfrac{24573}{4096}}\)
Which gives;
The sum of the 5th to the 13th term = S₁₃ - S₄
Therefore;
\(The \ sum \ of \ the \ 5th \ to \ the \ 13th \ term =\dfrac{24573}{4096} - \dfrac{45}{3} = \dfrac{1533}{4096} \approx \mathbf{0.374}\)
The value of the sum of the terms of the series is approximately 0.374Learn more about geometric series here:
https://brainly.com/question/12471913
On average, Nathaniel drinks
4/5 of a 10-ounce glass of water in
2 2/5
hours. How many glasses of water does he drink in one hour? Enter your answer as a whole number, proper fraction, or mixed number in simplest form.
Answers
Nathaniel drinks 3 glasses of water in one hour.
To find out how many glasses of water Nathaniel drinks in one hour, we need to calculate his drinking rate per hour.
In 2 2/5 hours, Nathaniel drinks 4/5 of a 10-ounce glass of water.
Let's convert the mixed number of hours to an improper fraction:
\(2\frac{2}{5} = \frac{(5 \times2 + 2)}{5}\)
\(=\frac{12}{5}\)
Now, we can set up a proportion to find his drinking rate per hour.
We know that \(\frac{12}{5}\) hours corresponds to \(\frac{4}{5}\) of a glass of water.
Let's assign "x" as the number of glasses he drinks in one hour.
The proportion is then
\(\frac{(\frac{12}{5} hours) }{(x glasses) } =\frac{(\frac{4}{5} glass)}{(1 hour)}\)
Cross-multiplying gives us
\((\frac{12}{5} )\times1=\frac{4}{5}\times(x)\)
Simplifying, we get
\(\frac{12}{5} =\frac{4}{5}\times x\)
Dividing both sides by \(\frac{4}{5}\), we find x:
\(x=\frac{(\frac{12}{5} )}{\frac{4}{5} }\)
\(x=\frac{12}{4}\)
\(x = 3.\)
Therefore, Nathaniel drinks 3 glasses of water in one hour.
For such more such question on glasses
https://brainly.com/question/11980886
#SPJ8
simple ratio of 13km to 3km
Answers
The simple ratio of 13 km to 3 km as required to be determined in the task content is; 13 : 3.
What is the simple ratio of 13km to 3km?It follows from the task content that the simple ratio of 13 km to 3 km is to be determined as required.
On this note, we have that;
13 km to 3 km.
which results to;
13 : 3
However, since 13 and 3 have no common factors except 1; it follows that the result as a simple ratio is; 13 : 3.
Read more on simple ratio;
https://brainly.com/question/29272642
#SPJ1
Which of the numbers below correctly describes 25 A?
Answers
The required number below correctly describes 25 A is 0.025 KA. Option A is correct.
What is a unit of measurement?Unit of measurement is defined as every entity having its measures in dimensions, weight, and time. Such as for length we have a meter, for liquid we have liters, and so on.
Here,
25 A is the unit of current,
Now,
This unit can be further written as,
25 A = 25 × KA / 1000 = 0.025 KA
The required number below correctly describes 25 A is 0.025 KA. Option A is correct.
Learn more about measurement here:
brainly.com/question/12629581
#SPJ1
Complete question-
which of the numbers below correctly describes 25 A? a) .025 KA, b) .25KA, c) 25,000 uA, d) 2500 mA
PLEASE HELP. I NEED TO GET THIS RIGHT

Answers
Ciro is right
Gerard is wrong
Gunther is also wrong
Equal expression:
1 - 2(40x - 12)
6 math books weigh 24 pounds. How much does 18 math books weigh?
Answers
Answer:
72 pounds
Step-by-step explanation:
6/24=18/x
cross multiply
Answer:
5 book because divide weight 24 for 1 and you go multiplication for 2 3 4 5 6
Step-by-step expl.klanation:
Need some help on questions 7&8

Answers
The missing angles of the triangles using law of cosines are:
7) x = 52.41°
8) x = 117.82°
How to use Law of cosine?The Law of Cosines (also called the Cosine Rule) says that:
c² = a² + b² − 2ab cos(C). It helps us solve some triangles.
7) Using cosine rule, we can find the angle x. Thus:
20² = 18² + 25² - 2(25 * 18) * cos x
400 = 324 + 625 - 900 cos x
900 cos x = 549
cos x = 549/900
cos x = 0.61
x = cos⁻¹(0.61)
x = 52.41°
8) Using cosine rule, we can find the angle x. Thus:
15² = 12² + 5² - 2(12 * 5) * cos x
225 = 169 - 120 cos x
56 = -120 cos x
cos x = -56/120
cos x = -0.4667
x = 117.82°
Read more about Law of cosine at: https://brainly.com/question/4372174
#SPJ1
What is the volume of this pyramid?
Enter your answer in the box.

Answers
Answer:
9576
Step-by-step explanation:
Area of the triangle × height
(1/2×28×19)×36
A quadratic function
y=f(x) is plotted on a graph and the vertex of the resulting parabola is (3,5). What is the vertex of the function defined as g(x)=f(x)−3
Answers
Since g(x) is a transformation of f(x) and the "-3" is outside the f(x) notation, the transformation will effect the y-values of the points on the graph of f(x).
What will subtracting 3 from every y-value of every point on the graph of f(x) do to the graph?
And more specifically, what will that do to the vertex that was at the point (3,5)?
Answer:
(-3, 2)
Step-by-step explanation:
reflect over the y axis, and then shift down 3 units.
whats the value of 2 over 21 minus 1 over 3
Answers
Answer:
2/21-1/3=2-7/21=-5/21
Answer this correctly I’ll give u brainalist + 10 points

Answers
Answer:
c
Step-by-step explanation:
Answer:
C. II and III
Step-by-step explanation:
Vertical angles are all start across from each other.
So:
∠3 and ∠6 are across from each other
∠2 and ∠5 are across from each other
∠1 and ∠4 are across from each other
The only option with at least two of the true statements above is C.
An insurance policy sells for $1000. Based on past data, an average of 1 in 50 policyholders will file a $20,000 claim, an average of 1 in 200 policyholders will file a $30,000 claim, and an average of 1 in 400 policyholders will file a $60,000 claim. a. Find the expected value (to the company) per policy sold.
Answers
The expected value (to the company) per policy sold is $630 and the expected profit is $6,300,000.
Expected valuea. Expected value of the claim:
Expected value=20,000 (1/200)+30,000(1/200)+60,000(1/500)
Expected value=100+150+120
Expected value=370
Expected value of the company profit:
Expected value=1,000-370
Expected value=630
b. If the company sells 10,000 policies the expected profit is:
Expected profit=10,000×630
Expected profit=$6,300,000
Therefore the expected value (to the company) per policy sold is $630 and the expected profit is $6,300,000.
Learn more about expected value here:https://brainly.com/question/24305645
#SPJ1
The complete question is:
An insurance policy sells for $1000. Based on past data, an average of 1 in 50 policyholders will file a $20,000 claim, an average of 1 in 200 policyholders will file a $30,000 claim, and an average of 1 in 400 policyholders will file a $60,000 claim.
a. Find the expected value (to the company) per policy sold.
b. If the company sells 10,000 policies, what is the expected total profit or loss for the company?
The following table shows the number of classes that each teacher in the math department at Wilburton High School teaches. Find the median number of classes.

Answers
Answer:
4 classes
Step-by-step explanation:
4+3+5+9+3+4=28
28/6=4.6
A regular octagon has a side of approximately 6.2 cm and an apothem of approximately 7.5 cm.Find the area of the octagon.
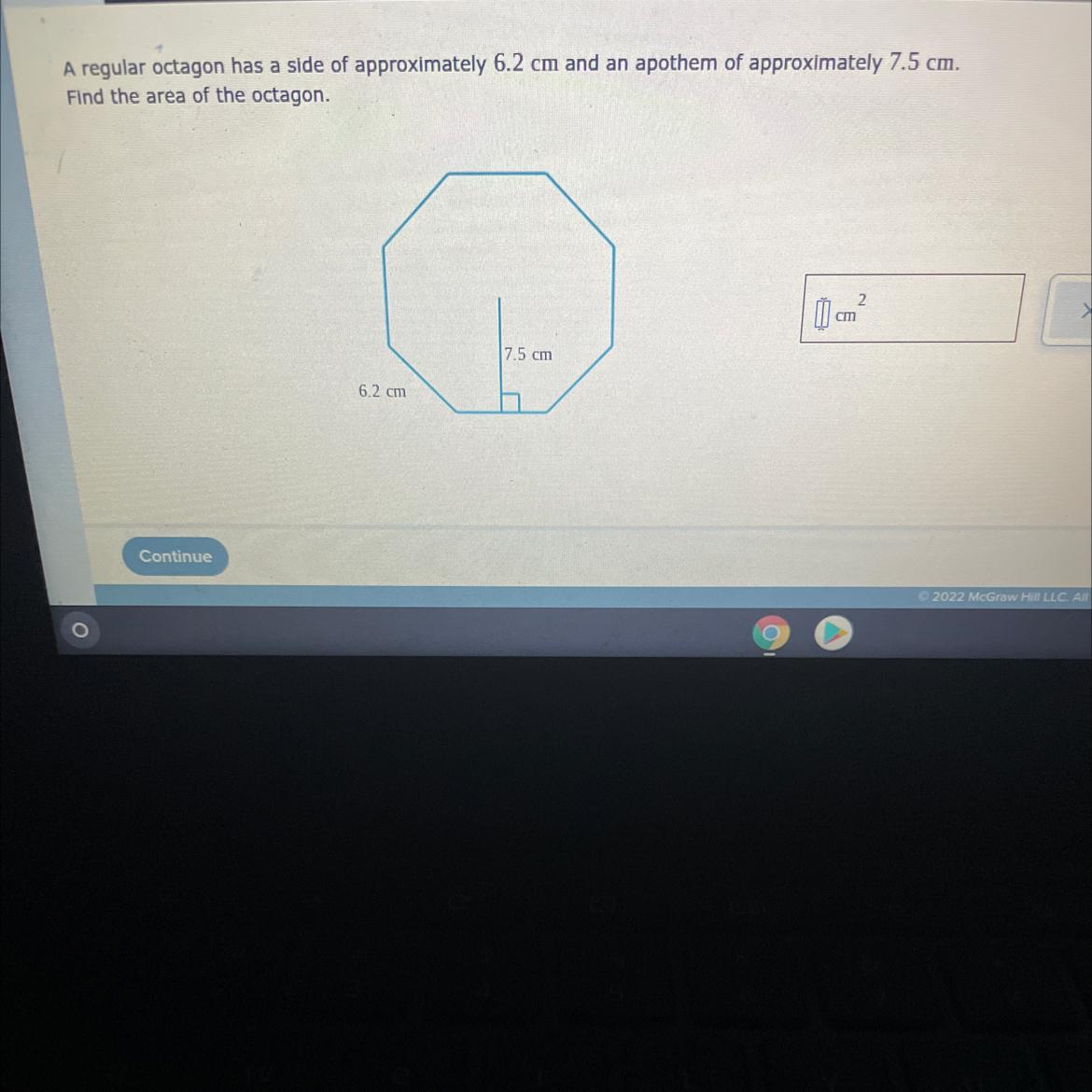
Answers
Given:
The side of a regular octagon = 6.2 cm
The apothem of a regular octagon = 7.5 cm
To find- the area of the octagon.
Explanation-
We know that octagon is divided into 8 small triangles.
The area of one triangle is computed below.
\(\begin{gathered} Area=\frac{1}{2}\times base\times height \\ Area=\frac{1}{2}\times6.2\times7.5 \\ Area=3.1\times7.5 \\ Area=23.25cm^2 \end{gathered}\)Thus, the area of the octagon will be
\(\begin{gathered} =8\times23.25 \\ =186cm^2 \end{gathered}\)The answer is 186cm^2.
Shadows. If a tree casts a 35-foot shadow at the same
time as a man 6 feet tall casts a 5-foot shadow, how tall is
the tree? [Section 9.5]
Answers
Please help and show how you found the answer step by step.
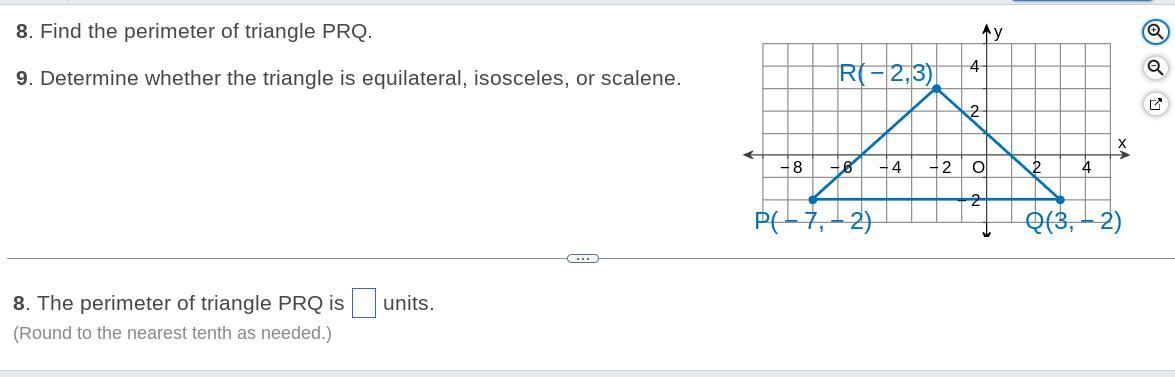
Answers
According to the information, the perimeter of the triangle is ≈ 31.18
How to calculate the perimeter of the triangle?To find the distance between two points, we can use the distance formula:
distance = sqrt((x2 - x1)^2 + (y2 - y1)^2)
Let's label the coordinates as follows:
Point 1: (-2, 3)
Point 2: (3, -2)
Now we can substitute these values into the distance formula:
distance = sqrt((3 - (-2))^2 + (-2 - 3)^2)
distance = sqrt((5)^2 + (-5)^2)
distance = sqrt(25 + 25)
distance = sqrt(50)
distance ≈ 7.07
Therefore, the distance from (-2, 3) to (3, -2) is approximately 7.07 units.
To find the perimeter of the triangle, we need to find the length of all three sides of the triangle and then add them up.
Using the distance formula, we can find the length of the sides:
Side 1: (-2,3) to (3,-2)
d = √[(3 - (-2))^2 + (-2 - 3)^2]
= √[5^2 + (-5)^2]
= √50
= 5√2
Side 2: (3,-2) to (-7,-2)
d = √[(-7 - 3)^2 + (-2 - (-2))^2]
= √[(-10)^2 + 0^2]
= 10
Side 3: (-7,-2) to (-2,3)
d = √[(-2 - (-7))^2 + (3 - (-2))^2]
= √[5^2 + 5^2]
= 5√2
Therefore, the perimeter of the triangle is:
5√2 + 10 + 5√2 = 15√2 + 10 ≈ 31.18 (rounded to two decimal places)
An two of the three sides are equal, so it is an isosceles triangle.
Lean more about isosceles triangle in: https://brainly.com/question/2456591
#SPJ1
Chandler decided to go cliff jumping into the lake at his cottage. He started on the cliff at 32 ft above sea level. He jumped for 40 feet! How far below sea level did Chandler end up?
Answers
Chandler ended up 8 feet below sea level. The negative sign indicates that his final position is below sea level. This means that he has descended further into the lake compared to the starting point on the cliff.
Chandler started on the cliff at 32 feet above sea level. When he jumped for 40 feet, we need to determine the final position in relation to sea level.
Since Chandler jumped down, the distance below sea level will be calculated as a negative value. To find how far below sea level Chandler ended up, we subtract the jump distance (40 feet) from the starting height (32 feet above sea level):
32 feet - 40 feet = -8 feet
It's important to note that negative values are used here to represent the direction and magnitude of Chandler's descent relative to sea level
For more such questions on feet
https://brainly.com/question/30403118
#SPJ8
Answer:
-8 feet
Step-by-step explanation:
As the CAPS document outlines, the Content Specification and Content Clarification for Patterns, Functions, and Algebra shows sequenced mathematics content topics and a content area spread. In the Intermediate Phase, select one topic and report on the topic sequence and content area spread. Your report should demonstrate mathematics concepts and procedures’ hierarchical and logical progression.
Answers
Answer:
Step-by-step explanation:
In the Intermediate Phase of mathematics education, one topic that demonstrates a hierarchical and logical progression in patterns, functions, and algebra is the concept of "Linear Equations."
The topic of Linear Equations in the Intermediate Phase builds upon the foundation laid in earlier grades and serves as a stepping stone towards more advanced algebraic concepts. Here is an overview of the topic sequence and content area spread for Linear Equations:
Introduction to Variables and Expressions:
Students are introduced to the concept of variables and expressions, learning to represent unknown quantities using letters or symbols. They understand the difference between constants and variables and learn to evaluate expressions.
Solving One-Step Equations:
Students learn how to solve simple one-step equations involving addition, subtraction, multiplication, and division. They develop the skills to isolate the variable and find its value.
Solving Two-Step Equations:
Building upon the previous knowledge, students progress to solving two-step equations. They learn to perform multiple operations to isolate the variable and find its value.
Writing and Graphing Linear Equations:
Students explore the relationship between variables and learn to write linear equations in slope-intercept form (y = mx + b). They understand the meaning of slope and y-intercept and how they relate to the graph of a line.
Systems of Linear Equations:
Students are introduced to the concept of systems of linear equations, where multiple equations are solved simultaneously. They learn various methods such as substitution, elimination, and graphing to find the solution to the system.
Word Problems and Applications:
Students apply their understanding of linear equations to solve real-life word problems and situations. They learn to translate verbal descriptions into algebraic equations and solve them to find the unknown quantities.
The content area spread for Linear Equations includes concepts such as variables, expressions, equations, operations, graphing, slope, y-intercept, systems, and real-world applications. The progression from simple one-step equations to more complex systems of equations reflects a logical sequence that builds upon prior knowledge and skills.
By following this hierarchical progression, students develop a solid foundation in algebraic thinking and problem-solving skills. They learn to apply mathematical concepts and procedures in a systematic and logical manner, paving the way for further exploration of patterns, functions, and advanced algebraic topics in later phases of mathematics education.
Which expression is equivalent to cos 150°?
three choices are:
A. cos 30°
B. cos 330°
C. cos (-30°)
D. cos (-210°)
Answers
We know
\(\boxed{\sf cos(180-\Theta)=-cos\Theta}\)
Now
\(\\ \sf{:}\!\!\implies cos150\)
\(\\ \sf{:}\!\!\implies cos(180-30)\)
\(\\ \sf{:}\!\!\implies -cos30\)
or
\(\\ \sf{:}\!\!\implies cos(-30°)\)
Option C
*I am greater than 80
*I am less than 90
*I am an even number
*My digits (of the mystery number) add up to 12
What’s my number
Answers
Answer:
Step-by-step explanation:
84?
8+4 is 12, and 84 is greater than 80, and less than 90
Answer:
84
Step-by-step explanation:
Find A and B if the graph of Ax + By = 12 passes through (2, 1) and is parallel to the graph of 2x − 7y = 3.
HELLPPPPPP
Answers
Answer:
A=-2 and B=7
Equation is -2x+7y=3
Step-by-step explanation:
A line can be represented by the equation y = 3x - 7.a. What is the slope? b. What are the coordinates of the y-intercept?
Answers
We will have the following:
From the expression:
\(y=3x-7\)From this, we can see that:
a. The slope is 3.
b. The coordinates of the y-intercept (0, -7).
100 POINTS BRAINLIEST AND THANKS!!!!

Answers
Answer:
1. $19,282.025
2.$3698
Step-by-step explanation:
1.
In order to calculate this, we can use the following formula:
\(\boxed{\bold{FV = PV(1 + \frac{r}{n})^{nt}}}\)
Where:
FV = Future Value PV = Present Value r = Annual interest rate n = Number of times interest is compounded per year t = Number of yearsIn this case, the following values would be used:
FV = ?PV = $3,294 r = 15%=0.15 n = 4t = 12Plugging these values into the formula, we get:
\(FV = 3,294(1 + \frac{0.15}{4})^{4*12}\)
= $19,282.025
2
In order to calculate this, we can use the following formula:
\(\boxed{\bold{FV = PVe^{rt}}}\)
Where:
FV = Future Value PV = Present Value r = Annual interest rate t = Number of yearsIn this case, the following values would be used:
FV = ?PV = $2,580r = 3%=0.03t = 12value of e= 2.7183Plugging these values into the formula, we get:
\(FV = 2,580e^{0.03*12}\)
= $3,697.99=$3698
Watch help video
The point A is plotted on the coordinate grid below. Plot the point A', the reflection
of A over the x-axis.
Click on the graph to plot a point. Click a point to delete it.
5
3
N
A
T
3
2
1
2
A
3
5
Answers
Answer:
The answer is point A' (3, -2).
A car is traveling at a rate of 108 kilometers per hour. What is the cars rate in meters per second? How many meters will the car travel in 20 seconds?
Answers
Answer:
\(\frac{30meters}{second}\)
600meters
Step-by-step explanation:
Use conversion factors that represent 1. You can cross cancel wods just like numbers.
\(\frac{108km}{1hour}\) · \(\frac{1hour}{60 minutes}\) · \(\frac{1minute}{60seconds}\) ·\(\frac{1000meters}{1 km}\)
\(\frac{108000meters}{3600seconds}\)
\(\frac{30meters}{second}\)
\(\frac{30meters}{second}\) ·\(\frac{20seconds}{1}\)
600 meters
Helping in the name of Jesus.
2. Determine the cost to cover the top of the fire pit with a piece of sheet metal that costs $25 per square foot. (6 points)
3. Determine the cost to lay down pebbel in the seating area one bag of pebbels covers 5 ft² and costs $8.99

Answers
39
I put that and got it right :)
On June 8, 1992, a crop circle with an 18-meter radius was found in a wheat field near Szekesfehervar, 43 miles southwest of Budapest. Find its circumference. Use 3.14 for pi.
Answers
Answer:
C = 113.04 mStep-by-step explanation:
circumference of a circle = 2πr
where
radius (r) = 18m
π = 3.14
plugin values into the formula
C = 2 (3.14) 18
C = 113.04 m
What is the difference between Independent and dependent events?
Choose the correct answer below.
O A Two events are independent when the occurrence of one event does not affect the probability of the occurrence of the other event. Two events are dependent when the occurrence of one event affects the probability
of the occurrence of the other event.
OB. Two events are independent if only one of the two events can occur. Two events are dependent if they can occur at the same time.
OC. Two events are independent when the occurrence of one event affects the probability of the occurrence of the other event. Two events are dependent when the occurrence of one event does not affect the probability
of the occurrence of the other event
OD. Two events are independent if they can occur at the same time. Two events are dependent if only one of the two events can occur.
Answers
Answer: A
Step-by-step explanation:
It is the definition of independent and dependent events
Which statement about x2 + 10x = 11 is true?
Answers
Equations are statements that have equal values, when compared
The true statement about \(x^2 + 10x = 11\) are x = 1 and x = -11
How to determine the true statementThe equation is given as:
\(x^2 + 10x = 11\)
Rewrite as:
\(x^2 + 10x - 11 = 0\)
Expand
\(x^2 + 11x - x - 11 = 0\)
Factorize
\(x(x + 11) -1( x + 11) = 0\)
Factor out x + 11
\((x -1)(x + 11) = 0\)
Solve for x
x = 1 or x = -11
Hence, the true statement about \(x^2 + 10x = 11\) are x = 1 and x = -11
Read more about equations at:
https://brainly.com/question/1214333