what is 6.85 times 2 times 10?
Answers
Answer:
137
Step-by-step explanation:
:)
Related Questions
how many integers between 100 and 999, inclusive, have the property that some permutation of its digits is a multiple of 11 between 100 and 999? for example, both 121 and 211 have this property. (2017amc10a problem 25)
Answers
226 integers are present between 100 and 999, inclusive, and have the property that some permutation of its digits is a multiple of 11 between 100 and 999.
Here, we have,
The problem statement is to find the number of multiples of 11 between 100 and 999 inclusive, where some multiples may have digits repeated twice and some may not.
To solve this problem, we can first count the number of multiples of 11 between 100 and 999 inclusive, which is 81.
Some of these multiples may have digits repeated twice, and each of these can be arranged in 3 permutations.
Other multiples of 11 have no repeated digits, and each of these can be arranged in 6 permutations.
However, we must account for the fact that switching the hundreds and units digits of these multiples also yields a multiple of 11, so we must divide by 2, giving us 3 permutations for each of these multiples.
Thus, we have a total of 81 × 3 = 243 permutations.
However, we have overcounted because some multiples of 11 have 0 as a digit.
Since 0 cannot be the digit of the hundreds place, we must subtract a permutation for each of these multiples.
There are 9 such multiples (110, 220, 330, ..., 990), yielding 9 extra permutations.
Additionally, there are 8 multiples (209, 308, 407, ..., 902) that also have 0 as a digit, yielding 8 more permutations.
Therefore, we must subtract these 17 extra permutations from the total of 243, giving us 226 permutations in total.
Learn more about permutations on
brainly.com/question/30649574
#SPJ12
need help pleaseeeeeeeee

Answers
The equation of the line of best fit is ŷ = 0.06x + 2.57
How to determine the equation of the line of best fitFrom the question, we have the following parameters that can be used in our computation:
Years Since 2000 0 1 2 3 4 5 6 7 8 9
Average Cost ($) 2.59 2.81 2.65 2.67 2.88 2.70 2.85 2.88 3.17 3.24
Next, we enter the above values in a graphing tool;
The calculation summary are as follows
Sum of X = 45Sum of Y = 28.44Mean X = 4.5Mean Y = 2.844Sum of squares (SSX) = 82.5Sum of products (SP) = 4.94The regression equation is represented as
ŷ = bx + a
Where
b = SP/SSX = 4.94/82.5 = 0.06
a = MY - bMX = 2.84 - (0.06*4.5) = 2.57
So, we have
ŷ = 0.06x + 2.57
Hence, the equation of the line of best fit is ŷ = 0.06x + 2.57
Read more about line of best fit at
https://brainly.com/question/30668844
#SPJ1
Solve the equation:
7x − 2 = 26
Answers
Answer:
\( \large \boxed{x = 4}\)
Step-by-step explanation:
Goal
Solve for x-term.Given
Equation\(7x - 2 = 26\)
Step 1
Isolate x by adding 2 to both sides.\(7x - 2 + 2 = 26 + 2 \\ 7x + 0 = 28 \\ 7x = 28 \\ x = \frac{28}{7} \\ x = 4\)
Step 2 (Optional)
We check the answer by substituting x = 4 in the equation.\(7x - 2 = 26 \\ 7(4) - 2 = 26 \\ 28 - 2 = 26 \\ 26 = 26\)
The equation is true for x = 4. Hence, the solution is x = 4.
1 If 2x+2 = 32, then x =
Answers
PLEASE HELP!!!!!!!!!!!!!!!!!!!!!!!!!
Which of the following is a solution to the equation x3=149 ?
A
x=723
B
x=732
C
x=7−23
23
D
x=7−32
E
This equation has no solution
Answers
Answer:
x=5.301459
You have to find the cube root of 149 to isolate the variable.
Answer:
E
Step-by-step explanation:
The graph of y = x is shown on the grid below.y412+A++-4-2++++ 22 4-2-44Which of the following is the graph of y = x + 1?

Answers
Recall that the graph of h(x+n) is the graph of h(x) translated n units to the left, therefore, the graph of
\(y=\sqrt[]{x+1}\)is the graph of
\(y=\sqrt[]{x}\)translated 1 unit to the left.
Answer:

Question 2 of 21
What is the solution to the system of equations graphed below?
O
A. (6,0)
OB. (0,6)
O C. (1,5)
D. (0, 3)

Answers
The solution to the system of equations graphed below is (1, 5)
Solution to system of equationThe given graph shows 2 lines intersecting at a point (x, y). This point of intersection is equivalent to the solution to the graphed function.
Tracing the points to the x and y-axis on the plane respectively will give the coordinate point (1, 5)
Hence the solution to the system of equations graphed below is (1, 5)
Learn more on system of equation here: https://brainly.com/question/25976025
#SPJ1
there is a single sequence of integers $a 2$, $a 3$, $a 4$, $a 5$, $a 6$, $a 7$ such that \[\frac{5}{7}
Answers
The given equation is$\frac{5}{7}=\frac{a_2}{a_3}\times \frac{a_4}{a_5}\times \frac{a_6}{a_7}$Now, let us take $a_2=5$ and $a_4=1$. Thus, we get, $\frac{5}{7}=\frac{5}{a_3}\times \frac{1}{a_5}\times \frac{a_6}{a_7}$To simplify, we get, $\frac{5a_5a_6}{7a_3a_7}=1$
Hence\(, $5a_5a_6=7a_3a_7$Now, let us take $a_5=7$, $a_6=1$, $a_3=5$ and $a_7=1$.\)Putting the values, we get, $5\times7\times1=7\times5\times1$.Thus,\($a_2=5$, $a_3=5$, $a_4=1$, $a_5=7$, $a_6=1$ and $a_7=1$\) satisfies the given equation $\frac{5}{7}=\frac{a_2}{a_3}\times \frac{a_4}{a_5}\times \frac{a_6}{a_7}$.
Therefore, there is a single sequence of integers \($a_2$, $a_3$, $a_4$, $a_5$, $a_6$, $a_7$\)such that $\frac{5}{7}=\frac{a_2}{a_3}\times \frac{a_4}{a_5}\times \frac{a_6}{a_7}$ and the values are: \($a_2=5$, $a_3=5$, $a_4=1$, $a_5=7$, $a_6=1$ and $a_7=1$.\)
To know more about integers visit:
https://brainly.com/question/24057012
#SPJ11
please help like waaa everywhere it comes up that its impossible

Answers
Answer:
Step-by-step explanation:
If we subtract 7 from both sides, we get -2 on the right. This is not possible, since absolute values are always 0 or greater.
Proving the Parallelogram Diagram Theorem
Given: ABCD is a Parallelogram. Diagonals AC,BD intersect at E.
Prove AE = CE and BE =DE
THE AWNSWERS ARE IN THE PICTURE FROM 4 DOWN SOME POSTED A PICTURE WITH THE 4 UP HERE TO HELP :)

Answers
Answer:
Did you learn about equal rectangles? we can prove AEB and CED are equal, which results in what we need to prove here
AE = CE and BE = DE. This can be proved with the help of the properties of congruent triangles.
What is a parallelogram?'A parallelogram is a special kind of quadrilateral that is formed by parallel lines. The angle between the adjacent sides of a parallelogram may vary but the opposite sides need to be parallel for it to be a parallelogram. A quadrilateral will be a parallelogram if its opposite sides are parallel and congruent.'
According to the given problem,
ABCD is a parallelogram.
We know,
BC ║ AD and BC ≅ AD
From, the properties of a parallelogram,
∠CBD = ∠ADB
∠BCA = ∠DAC
We know, two lines are parallel and alternate interior angles of the parallelogram are equal.
Also, Δ BEC ≅ ΔAED (Angle-Side-Angle)
Therefore, AE ≅ CE ( The properties of congruent triangles )
BE ≅ DE ( The properties of congruent triangles )
Hence, we can conclude, in the parallelogram ABCD, AE = CE and BE = DE from the properties of congruent triangles.
Learn more about parallelogram here: https://brainly.com/question/11220936
#SPJ2
Question content area top
Part 1
Find the length x to the nearest whole number.
43°
22°
507
x
Question content area bottom
Part 1
x≈ enter your response here
(Round to the nearest whole number as needed.)
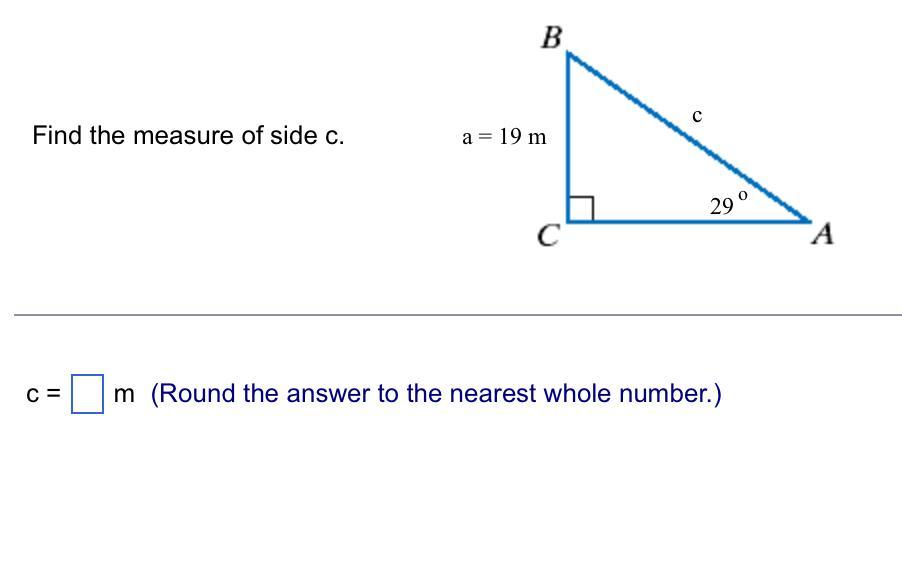
Answers
In the given triangle, the measure of side c is approximately 39 m
Trigonometry: Calculating the measure of side c in the triangleFrom the question, we are to calculate the measure of side c in the given triangle.
To determine the measure of side c, we will use SOH CAH TOA
sin (angle) = Opposite / Hypotenuse
cos (angle) = Adjacent / Hypotenuse
tan (angle) = Opposite / Adjacent
In the given diagram,
Angle = 29°
Opposite = 19 m
Hypotenuse = c
Thus
sin (29°) = 19 / c
0.4848 = 19 / c
c = 19 / 0.4848
c = 39.1914
c ≈ 39 m
Hence,
The measure of c is 39 m
Learn more on Trigonometry here:
https://brainly.com/question/31387901
#SPJ1
find the area of the kite below. A= blank

Answers
The area of the kite is 168 square units.
Area of kite
The general form of area of a kite is calculated by half the product of the lengths of its diagonals.
Then the formula to determine the area of a kite is:
Area = ½ × (d)1 × (d)2.
where (d)1 and (d)2 are long and short diagonals of a kite.
Given,
Here we have the diagram of the kite with side values.
Now, we have to find the area of the kite.
In order to find the area of the kite,
We have to identify the diagonals of the kite,
Here the values of the diagonals are 12 and 13.
Then the area of the kite is calculated as,
=> A = 1/2 x 24 x 14
=> A = 12 x 14
=> A = 168
Therefore the area of the kite is 168 square units.
To know more about Area of Kite here.
https://brainly.com/question/15640807
#SPJ1
Ellora wants to accumulate $150000.00 in an RRSP by making annual contributions of $5000.00 at the beginning of each year. If interest is 5.5% compounded quarterly, calculate how long she has to make contributions.
a. 18.202125
b. 18.676765
c. 17.455483
d. 17.585794
e. 18.076686
Answers
Option A is the correct answer. Ellora wants to accumulate 150,000 in an RRSP by making annual contributions of 5,000 at the beginning of each year. If interest is 5.5% compounded quarterly, calculate how long she has to make contributions.
First, we have to find the interest rate per quarter, which will be
\(5.5% / 4\)= 1.375%.
The formula for the future value of an annuity is:
\(FV = (C * [(1 + r)^n - 1] / r)\),
For Ellora, \(FV = $150,000, C = $5,000, and r = 1.375%.\)
Substituting these values into the formula gives:
\(150,000 = 5,000 * [(1 + 0.01375)^n - 1] / 0.01375\)
Simplifying this equation gives:
\(30 = [(1.01375)^n - 1]\)
We can solve this using logarithms:
\(ln 30 = ln [(1.01375)^n - 1]\)
\(ln 30 = n * ln 1.01375 - ln 1.01375e^(ln 30) / e^(-ln 1.01375) = n18.202125 = n\)
Therefore, it will take Ellora 18.202125 years to accumulate 150,000 in her RRSP through \($5,000\)annual contributions made at the beginning of each year with interest of \(5.5%\) compounded quarterly.
To know more about compounded quarterly visit:-
https://brainly.com/question/29021564
#SPJ11
Find the exact coordinates of the point at which the following curve is steepest: y = 50/1+ 6e^-2t for greaterthanorequalto 0
Answers
Since the exponential function is always positive, there is no solution for e^(-2t) = -1/6. This means that the derivative is never equal to zero, and there is no point of maximum steepness for this curve.
To find the point at which the curve is steepest, we need to find the maximum value of the derivative of the function. Let's start by finding the derivative of the given function:
y = 50 / (1 + 6e^(-2t))
To find the derivative, we can use the quotient rule:
y' = [50(0) - (1 + 6e^(-2t))(-12e^(-2t))]/(1 + 6e^(-2t))^2
Simplifying this expression, we get:
y' = (72e^(-2t))/(1 + 6e^(-2t))^2
To find the maximum point, we need to find the value of t for which the derivative is equal to 0. Setting y' = 0 and solving for t, we have:
(72e^(-2t))/(1 + 6e^(-2t))^2 = 0
Since the numerator cannot be zero, we focus on the denominator:
(1 + 6e^(-2t))^2 = 0
Taking the square root of both sides, we get:
1 + 6e^(-2t) = 0
Solving for e^(-2t), we have:
e^(-2t) = -1/6
Learn more about exponential function visit:
brainly.com/question/28596571
#SPJ11
What is 2000+400-300=
Answers
Answer:
2100
Step-by-step explanation:
2000+400= 2400
2400-300= 2100
Sin Cos Tan questions
1. If cosA= 21/29, what is the perimeter of the triangle
2. If sinA-10/26, what is the perimeter of the triangle?
3. If tanA=15/8, what is the perimeter of the triangle?
4. If cosA-12/37, what is the perimeter of the triangle?
5. If tanA-12/16, what is the perimeter of the triangle?

Answers
The perimeter of a triangle is the sum of all its sides.
What is triangle?Triangles is a 3×3 cited only going with three angles and three side it is one of the most basic fundamental safe in the geometry and is used in many different area of 10 science triangle are also after used in the architecture art in other area of the designing triangle came in many other different form.
To find the perimeter, we must first calculate the lengths of the sides of the triangle. To do this, we must use the properties of trigonometric functions.
In the first question, cos A = \(\frac{21}{29}\). Using the law of cosines, we know that \(a^{2}\) = \(b^{2}\) + \(c^{2}\) - 2bc cos A. Thus, the length of side a can be found by substituting the given values and solving for a.
In the second question, sin A = \(\frac{10}{26}\). Using the law of sines, we know that \(\frac{a}{sin A}\) = \(\frac{b}{sin B}\) = \(\frac{c}{sin C}\). Thus, the length of side a can be found by substituting the given values and solving for a.
In the third question, tan A = \(\frac{15}{8}\). Using the law of tangents, we know that \(\frac{a}{tan A}\) = \(\frac{b}{tan B}\) = \(\frac{c}{tan C}\). Thus, the length of side a can be found by substituting the given values and solving for a.
In the fourth question, cos A = \(\frac{12}{37}\). Using the law of cosines, we know that \(a^{2}\) = \(b^{2}\) + \(c^{2}\) - 2bc cos A. Thus, the length of side a can be found by substituting the given values and solving for a.
In the fifth question, tan A = \(\frac{12}{16}\). Using the law of tangents, we know that \(\frac{a}{tan A}\) = \(\frac{b}{tan B}\) = \(\frac{c}{tan C}\). Thus, the length of side a can be found by substituting the given values and solving for a.
Once we have the lengths of all sides, we can then calculate the perimeter of the triangle by simply adding all the side lengths together. Therefore, the perimeter of the triangle can be found by using the properties of trigonometric functions to calculate the lengths of the sides, and then adding all the side lengths together.
To know more about triangle click-
brainly.com/question/17335144
#SPJ1
Given y = 3x + 1 State the quadrants in which this graph is in. (Use the numbers 1-4)
Answers
Answer:
1, 2 and 3 (I, II and III)
Step-by-step explanation:
Since the slope is positive (3) in the equation y = 3x + 1, it means that the graph has a positive slope, meaning the line slopes up from left to right.
The y intercept is 1
the x intercept is:
0 = 3x + 1
x = 1/3
Therefore, the graph of y = 3x + 1 lies in quadrants I, II and III. Graph the equation to prove this.
Choose the function represented by the data a polynomial function is represented by the data in the table . 0 1 2 4 f(x) = x ^ 3 - x ^ 2 - 24; f(x) = (x ^ 3)/4 + 2x ^ 2 - 24; f(x); - 24 -14 3/3 * 3/4 24 - 21 3/4; f(x) = - 2 1/4 * x ^ 2 + 24; f(x) = 3/4 * x ^ 2 - 3x + 24
Answers
This is because the values of f(x) in the table match the corresponding values obtained by evaluating the polynomial function for the given input values of the function represented by the data a polynomial function is represented by the data is f(x) = x^3 - x^2 - 24.
A polynomial is an expression with more than two algebraic terms, especially the sum of several terms that contain different powers of the same variable. A polynomial function is a function that includes a polynomial expression with an independent variable (x) that can only take on integer values because of its discrete nature.
Choose the function represented by the data: The polynomial function represented by the data is f(x) = x^3 - x^2 - 24.
A table representing the function f(x) = x^3 - x^2 - 24 is shown below:
x | f(x)
0 | -24
1 | -14
2 | 0
4 | 40
Therefore, the function represented by the data is f(x) = x^3 - x^2 - 24.
The provided table displays the values of the function f(x) for different input values of x. By substituting the corresponding values of x into the function, we can observe the corresponding output values. This allows us to identify the pattern and equation that represents the function.
In this case, the table shows that when x is 0, the value of f(x) is -24. When x is 1, f(x) is -14. When x is 2, f(x) is 0. And when x is 4, f(x) is 40.
Based on these data points, we can conclude that the function represented by the data is f(x) = x^3 - x^2 - 24.
Learn more about polynomial function :
brainly.com/question/30474881
#SPJ11
We find that Option 2, f(x) = \((x^3)/4 + 2x^2 - 24\), matches the data given in the table.
Based on the data given in the table, we need to determine the polynomial function that represents the data.
To do this, we can compare the values of f(x) in the table with the given options for the polynomial functions. We are looking for a function that matches the given data points.
Let's evaluate each option using the x-values from the table:
Option 1: f(x) = \(x^3 - x^2 - 24\)
For x = 0,\(f(0) = 0^3 - 0^2 - 24 = -24\) (matches the data)
For x = 1, \(f(1) = 1^3 - 1^2 - 24 = -24 - 1 - 24 = -49\) (does not match the data)
For x = 2,\(f(2) = 2^3 - 2^2 - 24 = 8 - 4 - 24 = -20\) (does not match the data)
Option 2: \(f(x) = (x^3)/4 + 2x^2 - 24\)
For x = 0,\(f(0) = (0^3)/4 + 2(0^2) - 24 = 0 - 0 - 24 = -24\) (matches the data)
For x = 1,\(f(1) = (1^3)/4 + 2(1^2) - 24 = 1/4 + 2 - 24 = -20.75\)(does not match the data)
For x = 2, \(f(2) = (2^3)/4 + 2(2^2) - 24 = 8/4 + 8 - 24 = -14\)(matches the data)
Option 3: f(x) = -24 - 14(3/3)(3/4)
Simplifying, f(x) = -24 - 14(1)(3/4) = -24 - 14(3/4) = -24 - 10.5 = -34.5 (does not match the data)
Option 4: \(f(x) = -2 1/4 * x^2 + 24\)
For x = 0, \(f(0) = -2 1/4 * 0^2 + 24 = 24\) (does not match the data)
For x = 1,\(f(1) = -2 1/4 * 1^2 + 24 = -2 1/4 + 24 = 21.75\) (does not match the data)
For x = 2,\(f(2) = -2 1/4 * 2^2 + 24 = -2 1/4 * 4 + 24 = -9 + 24 = 15\) (does not match the data)
Option 5: \(f(x) = 3/4 * x^2 - 3x + 24\)
For x = 0, \(f(0) = 3/4 * 0^2 - 3(0) + 24 = 24\) (does not match the data)
For x = 1, \(f(1) = 3/4 * 1^2 - 3(1) + 24 = 3/4 - 3 + 24 = 21.75\) (does not match the data)
For x = 2,\(f(2) = 3/4 * 2^2 - 3(2) + 24 = 3/4 * 4 - 6 + 24 = 3 - 6 + 24 = 21\)(matches the data)
Learn more about polynomial function from the given link:
https://brainly.com/question/1496352
#SPJ11
2. 1
—. —
3 - 2
Think carefully???
Answers
Answer:
my head hurts now -.-
Step-by-step explanation:
If h = 3.5u, what is the value of h when u = 17?
Give any decimal answers to 1 d.p.
Answers
Put u=17
h=3.5(17)h=51+8.5h=59.5Answer:
59.5.
Step-by-step explanation:
h = 3.5u
When u = 17,
h = 3.5*17
= 59.5
Given that €1 =£0.72 a) how much is €410 b) what is the £ to € exchange rate ?
Answers
Answer:
As per the given statement: €1 = £0.72Find how much is €410 in £.then;€410 = = £295.2Hence, £295.2 much is €410.to find, the exchange rate of £ to €:€1 = £0.72Divide both sides by 0.72 we get;£1 = €1.38
I really need help on this please

Answers
Answer:
x = 6
Step-by-step explanation:
You use trig to find the hypotenuse of the first triangle. 4^2 + 3^2 = c^2. Then you get c = 5. SInce 10 is 2 times greater than 5 you multiply 3 by 2 and get 6. Hope that helps.
What is the value of X in the equation X - 1/2= 3 1/6
A. X=2 2/3
B. X = 3 2/3
C. X =4 1/6
D. X=6 1/3
Answers
Answer:
3 2/3
Step-by-step explanation:
\(x-\frac{1}{2} = 3 \frac{1}{6}\)
\(x-\frac{1}{2} = \frac{19}{6} \\x = \frac{19}{6} + \frac{3}{6} \\x = \frac{22}{6} \\x = 3 \frac{2}{3}\)
By what factor is Triangle 1 reduced to form Triangle 2?

Answers
\(▪▪▪▪▪▪▪▪▪▪▪▪▪ {\huge\mathfrak{Answer}}▪▪▪▪▪▪▪▪▪▪▪▪▪▪\)
The required scale factor is :
\(0.75\)Simplify. 2 × (3 – 1) + 3
Answers
100PTS BRAINLIEST! (only if you get them correct!!)


Answers
Answer:
A and F
Step-by-step explanation:
Jeremy goes on a bike ride for 45 minutes per day during the summer. At the end of the summer, he has rode his bike for 2,475 minutes. How many days did he ride his bike? He rode days.
Answers
Answer:
55 days
Step-by-step explanation:
1 day = 45 minutes
=> x days = 2475 ÷ 45
=> x days = 55 days
Therefore, he had rode 55 days in the whole summer.
Using a scale of 1 centimeter = 5 meters, what are the actual dimensions of the swimming pool?
Answers
The pool's new size will be 10 by 5 centimetres, where 1 centimetre equals 5 metres.
What are the swimming pool's exact measurements?An object can be resized by scaling. It can be to make the thing bigger or smaller.
assuming a rectangular pool with dimensions of 50 by 25 metres
Drawing the pool at scale, with 1 cm equaling 5 metres, as follows:
1 cm = 5m .... 1
For the length;
L = 50 m ..... 2
Divide expressions 1 and 2 together;
1/L = 5/50
5L = 50
L = 50/5
L = 10 cm
For the width:
Original width = 25 meters
Get the new width
1/W = 5/25
5W = 25
W = 25/5
W = 5 cm
This demonstrates that the pool's new size will be 10 cm by 5 cm.
To know more about dimensions, visit:
https://brainly.com/question/11187894
#SPJ1
The complete question and image of rectangular pool attached below,


The following statement contains an error. Choose the statement that best explains the error.
"The correlation between shoe size and height is 0.87 inches"
A. Correlation requires that both the variables be categorical
B. When stating the correlation coefficient, one must state whether it is a positive or negative relationship
C. This statement does not tell us whether or not shoe size is correlated with height
D. When reporting correlation, one does not report units because correlation has no units
E. There is no error in this statement
Answers
The error in the statement will be When reporting correlation, one does not report units because correlation has no units that is option D is correct.
The correct statement would be "The correlation between shoe size and height is 0.87." The correlation coefficient is a measure of the strength and direction of a linear relationship between two variables. It ranges from -1 to 1, with -1 indicating a strong negative relationship, 0 indicating no relationship, and 1 indicating a strong positive relationship. The correlation coefficient does not have units because it is a standardized measure of the relationship between the variables. If there is a unit given in any correlation statement then it means that the statement is a wrong statement or it has an error.
Learn more about Correlation at:
brainly.com/question/4219149
#SPJ4
Which of the following formulas which of the following formulas defines an arithmetic sequence?
a) tn = 5 + 14
b) tn= 5n² + 14
c) tn= 5n(n+14)
d) tn= 5n + 14
Answers
The correct formula that defines an arithmetic sequence is option d) tn = 5n + 14.
An arithmetic sequence is a sequence of numbers in which the difference between consecutive terms remains constant. In other words, each term can be obtained by adding a fixed value (the common difference) to the previous term.
In option a) tn = 5 + 14, the term does not depend on the value of n and does not exhibit a constant difference between terms. Therefore, it does not represent an arithmetic sequence.
Option b) tn = 5n² + 14 represents a quadratic sequence, where the difference between consecutive terms increases with each term. It does not represent an arithmetic sequence.
Option c) tn = 5n(n+14) represents a sequence with a varying difference, as it depends on the value of n. It does not represent an arithmetic sequence.
Option d) tn = 5n + 14 represents an arithmetic sequence, where each term is obtained by adding a constant value of 5 to the previous term. The common difference between consecutive terms is 5, making it the correct formula for an arithmetic sequence.
To more on Progression:
https://brainly.com/question/30442577
#SPJ8