what is 7/9 divided by 1/2?
Answers
Solve the quotient
\(\frac{\frac{7}{9}}{\frac{1}{2}}=\frac{7\cdot2}{9\cdot1}=\frac{14}{9}\)Related Questions
In the graph above, what's the distance between (0, 2) and (5, 2)?
Answers
Answer:
where is the graph
Step-by-step explanation:
Answer:
The distance is 5
Step-by-step explanation:
use the following function rule to find f (3).
f (x) = -5(2) ^x
f (3)=
Answers
Step-by-step explanation:
Substitute f(3) into the function:
\(f(3) = - 5(2)^{3} \)
Include exponent:
\(f(3) = - 5(8)\)
Multiply:
\(f(3) = - 40\)
In a study investigating the effect of car speed on accident severity, the vehicle speed at impact was recorded for 5,000 fatal accidents. For these accidents, the mean speed was 46 mph and the standard deviation was 13 mph. A histogram revealed that the vehicle speed distribution was mound shaped and approximately symmetric. (Use the Empirical Rule.) (a) Approximately what percentage of vehicle speeds were between 33 and 59 mph
Answers
Answer:
68%
Step-by-step explanation:
Given that:
Mean speed (m) = 46
Standard deviation (s) = 13
Approximately what percentage of vehicle speeds were between 33 and 59 mph
Obtain the Zscore for P(Z < x) for both values and subtract :
For x = 33
Zscore :
Z = (x - m) / s
Z = (33 - 46) / 13 = - 1
p(Z < - 1) = 0.15866 ( Z probability calculator)
For x = 59
Zscore :
Z = (x - m) / s
Z = (59 - 46) / 13 = 1
p(Z < 1) = 0.84134 ( Z probability calculator)
Hence, 0.84134 - 0.15866 = 0.68268 = 0.68
0.68 * 100% = 68%
Given tan theta =9, use trigonometric identities to find the exact value of each of the following:_______
a) sec sqr Theta
b) Cot theta
c) cot (pie/2-Theta)
d) csc sqr theta
Answers
Answer:
\((a)\ \sec^2(\theta) = 82\)
\((b)\ \cot(\theta) = \frac{1}{9}\)
\((c)\ \cot(\frac{\pi}{2} - \theta) = 9\)
\((d)\ \csc^2(\theta) = \frac{82}{81}\)
Step-by-step explanation:
Given
\(\tan(\theta) = 9\)
Required
Solve (a) to (d)
Using tan formula, we have:
\(\tan(\theta) = \frac{Opposite}{Adjacent}\)
This gives:
\(\frac{Opposite}{Adjacent} = 9\)
Rewrite as:
\(\frac{Opposite}{Adjacent} = \frac{9}{1}\)
Using a unit ratio;
\(Opposite = 9; Adjacent = 1\)
Using Pythagoras theorem, we have:
\(Hypotenuse^2 = Opposite^2 + Adjacent^2\)
\(Hypotenuse^2 = 9^2 + 1^2\)
\(Hypotenuse^2 = 81 + 1\)
\(Hypotenuse^2 = 82\)
Take square roots of both sides
\(Hypotenuse =\sqrt{82}\)
So, we have:
\(Opposite = 9; Adjacent = 1\)
\(Hypotenuse =\sqrt{82}\)
Solving (a):
\(\sec^2(\theta)\)
This is calculated as:
\(\sec^2(\theta) = (\sec(\theta))^2\)
\(\sec^2(\theta) = (\frac{1}{\cos(\theta)})^2\)
Where:
\(\cos(\theta) = \frac{Adjacent}{Hypotenuse}\)
\(\cos(\theta) = \frac{1}{\sqrt{82}}\)
So:
\(\sec^2(\theta) = (\frac{1}{\cos(\theta)})^2\)
\(\sec^2(\theta) = (\frac{1}{\frac{1}{\sqrt{82}}})^2\)
\(\sec^2(\theta) = (\sqrt{82})^2\)
\(\sec^2(\theta) = 82\)
Solving (b):
\(\cot(\theta)\)
This is calculated as:
\(\cot(\theta) = \frac{1}{\tan(\theta)}\)
Where:
\(\tan(\theta) = 9\) ---- given
So:
\(\cot(\theta) = \frac{1}{\tan(\theta)}\)
\(\cot(\theta) = \frac{1}{9}\)
Solving (c):
\(\cot(\frac{\pi}{2} - \theta)\)
In trigonometry:
\(\cot(\frac{\pi}{2} - \theta) = \tan(\theta)\)
Hence:
\(\cot(\frac{\pi}{2} - \theta) = 9\)
Solving (d):
\(\csc^2(\theta)\)
This is calculated as:
\(\csc^2(\theta) = (\csc(\theta))^2\)
\(\csc^2(\theta) = (\frac{1}{\sin(\theta)})^2\)
Where:
\(\sin(\theta) = \frac{Opposite}{Hypotenuse}\)
\(\sin(\theta) = \frac{9}{\sqrt{82}}\)
So:
\(\csc^2(\theta) = (\frac{1}{\frac{9}{\sqrt{82}}})^2\)
\(\csc^2(\theta) = (\frac{\sqrt{82}}{9})^2\)
\(\csc^2(\theta) = \frac{82}{81}\)
Write a linear function for the graph, and state and interpret the slope and y-intercept for the given scenario:
Bamboo grows very quickly. Use the information in the graph to write an equation that models the height (y) at time (x).
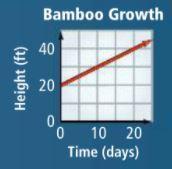
Answers
The linear function for the given graph is y = x + 20.
What is a linear function?
A straight line on the coordinate plane is represented by a linear function. It has one independent variable and one dependent variable. For slope (m) and y-intercept (b) form, the equation is given by:
y = mx + b
From the graph,
The coordinates of the given graph are (0,20) and (20,40)
Then, slope (m) = (40-20)/(20-0) = 20/20 = 1
and y-intercept (b) = 20
So, the equation will be y = 1x + 20
Hence, the linear function for the given graph is y = x + 20.
To learn more about a linear function
https://brainly.com/question/29213103
#SPJ1
Suppose 35.45% of small businesses experience cash flow problems in their first 5 years. A consultant takes a random sample of 530 businesses that have been opened for 5 years or less. What is the probability that between 34.2% and 39.03% of the businesses have experienced cash flow problems?
1) 0.6838
2) 20.3738
3) 0.3162
4) - 11.6695
5) 1.2313
Answers
Answer:
1) 0.6838
Step-by-step explanation:
To solve this question, we need to understand the normal probability distribution and the central limit theorem.
Normal Probability Distribution
Problems of normal distributions can be solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the z-score of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
Central Limit Theorem
The Central Limit Theorem establishes that, for a normally distributed random variable X, with mean \(\mu\) and standard deviation \(\sigma\), the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean \(\mu\) and standard deviation \(s = \frac{\sigma}{\sqrt{n}}\).
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
For a proportion p in a sample of size n, the sampling distribution of the sample proportion will be approximately normal with mean \(\mu = p\) and standard deviation \(s = \sqrt{\frac{p(1-p)}{n}}\)
35.45% of small businesses experience cash flow problems in their first 5 years.
This means that \(p = 0.3545\)
Sample of 530 businesses
This means that \(n = 530\)
Mean and standard deviation:
\(\mu = p = 0.3545\)
\(s = \sqrt{\frac{p(1-p)}{n}} = \sqrt{\frac{0.3545(1-0.3545)}{530}} = 0.0208\)
What is the probability that between 34.2% and 39.03% of the businesses have experienced cash flow problems?
This is the p-value of Z when X = 0.3903 subtracted by the p-value of Z when X = 0.342.
X = 0.3903
\(Z = \frac{X - \mu}{\sigma}\)
By the Central Limit Theorem
\(Z = \frac{X - \mu}{s}\)
\(Z = \frac{0.3903 - 0.3545}{0.0208}\)
\(Z = 1.72\)
\(Z = 1.72\) has a p-value of 0.9573
X = 0.342
\(Z = \frac{X - \mu}{s}\)
\(Z = \frac{0.342 - 0.3545}{0.0208}\)
\(Z = -0.6\)
\(Z = -0.6\) has a p-value of 0.27425
0.9573 - 0.2743 = 0.683
With a little bit of rounding, 0.6838, so option 1) is the answer.
Given that cosθ=817 and sinθ=−1517 . What is the value of tanθ?
Answers
Answer:
tan∅ = -1517/817
Step-by-step explanation:
tan∅ = sin∅/cos∅
Answer:
Step-by-step explanation:

Mr. hodges wants to build a fence
Answers
Answer:
96 feet
Step-by-step explanation: took quiz pls mark brainliest
Susan read 40 pages of a novel in 80 minutes. How long will it take her to read 210 pages of the novel?
Answers
Answer: It will take Susan 420 minutes to read 210 pages of her novel.
A rectangular shaped park contains two gardens of multi-colored roses. Sidewalks enclose the whole park and each of the gardens. What is the total
length of the sidewalks that surround these two gardens?
30 meters
20 meters
24 meters
20 meters
A.
134 meters
B
148 meters
C.
94 meters
х
D
144 meters

Answers
Answer:I say that would be 94
Step-by-step explanation:
because if you add all up it equals 94
How do you make a decimal into a fraction?
Answers
Answer:
Step 1: Write down the decimal divided by 1, like this: decimal 1.
Step 2: Multiply both top and bottom by 10 for every number after the decimal point. (For example, if there are two numbers after the decimal point, then use 100, if there are three then use 1000, etc.)
Step 3: Simplify (or reduce) the fraction.
Define associative property
Answers
Answer:
the way in which factors are grouped in a multiplication problem does not change the product.
Step-by-step explanation:
For his birthday, Zack and three of his friends went to a movie. They each got a ticket for $8.00 and the same snack from the concession stand. If Zack’s mom paid $48 for the group’s tickets and snacks, how much did each snack cost? The equation 4( s +8) = 48 represents the situation when s represents the cost, in dollars, of one snack.
Answers
Answer:
Which number is IRRATIONAL? A) √12 B) √36 C) √64 D) √144
Step-by-step explanation:
At a gas station, 50% of the customers use regular gas, 30% use mid-grade gas and 20% use premium gas. Of those customers using regular gas, only 30% fill their tanks. Of those customers using mid-grade gas, 60% fill their tanks, whereas of those using premium, 50% fill their tanks. What is the probability that the next customer will request mid-grade gas and fill the tank
Answers
Answer:
The probability that the next customer will request mid-grade gas and fill the tank is 0.1800
Step-by-step explanation:
In order to calculate the probability that the next customer will request mid-grade gas and fill the tank we would have to make the following calculation:
probability that the next customer will request mid-grade gas and fill the tank= percentage of the people using mid-grade gas* percentage of the people using mid-grade gas that fill their tanks
probability that the next customer will request mid-grade gas and fill the tank= 30%*60%
probability that the next customer will request mid-grade gas and fill the tank= 0.1800
The probability that the next customer will request mid-grade gas and fill the tank is 0.1800
ILL GIVE BRAINLY What is the surface area of the cube?
Drag and drop the correct surface area to match the cube.

Answers
Answer:
Below
Step-by-step explanation:
A cube has SIX sides of equal area
each side has area = L x W and L and W are the same = 4.5 m
so: Area = six X ( 4.5 X 4.5) = 6 * 4.5 * 4.5 = 121.5 m^2
Answer:
Hope the picture will help you...

can someone help me with this

Answers
Answer:
no clue
Step-by-step explanation:
a
Identify the x-intercept and y-intercept of the line 2x - 4y = - 12.
O The x-intercept is (-6,0) and the y-intercept is (0, 3).
O The x-intercept is (0, -6) and the y-intercept is (3,0).
O The x-intercept is (2,0) and the y-intercept is (0. - 4).
O The x-intercept is (0, 3) and the y-intercept is (-6,0).
Answers
The x-intercept of the given line is (-6,0) and y-intercept of the given line is (0,3)
To find the x-intercept:
x-intercept can be found by taking y = 0
The given equation is
2x - 4y = -12
Let us take y = 0, then
2x - 4(0) = -12
2x - 0 = -12
2x = -12
x = -12/2
x = -6
Therefore the x-intercept of the given line is (-6,0)
To find the y-intercept:
Similarly, y-intercept can be found by taking x = 0
The given equation is
2x - 4y = -12
Take x = 0, then
2(0) - 4y = -12
-4y = -12
4y = 12
y = 12/4
y = 3
Therefore, y-intercept of the given line is (0,3)
The x-intercept of the given line is (-6,0) and y-intercept of the given line is (0,3)
Learn more about the intercept in
https://brainly.com/question/14180189
#SPJ9
Enter an equation of the form y= mx for the line that passes through the
origin and has slope 13.

Answers
Answer:
y = 13x
Step-by-step explanation:
gradient = 13
x = 0
y = 0
\(\frac{Δy}{Δx}\)
so \(\frac{y - 0}{x - 0}\) = 13
cross multiply and you get
y = 13x
Select any to represent a and use it to complete the puzzle on the left.
Pls, help.

Answers
Please find attached the completed equation puzzle with the number 8 representing a, created with MS Word.
What is an equation?An equation is an expression of equivalence of the two expressions, quantities and or numbers, which are joined by the '=' sign.
The puzzle can be completed using both variables and values that satisfies equations created in the puzzle as follows;
Let a = 8, starting from top left of the puzzle, we get;
3·a + 4 = 3 × 8 + 4 = 28
The vertical column in the top middle with 28 at the top, indicates that we get the following equation;
28 + 4·a = 28 + 4 × 8 = 60
The row that crosses the middle of the vertical row above indicates that we get;
4·a + 4·a - 3·a = 5·a
The value, 3·a, obtained above is evaluated as; 3·a = 3 × 8 = 24
The vertical column with 6·a is evaluated as follows;
4·a + x = 6·a + a = 7·a
x = 7·a - 4·a = 3·a
x = 3·a
Therefore, we get; 4·a + 3·a = 6·a + a = 7·a
The values left blank are evaluated as follows;
a + 6·a - 3·a = 4·a
2·a + 4·a = 6·a
a + 6·a = 7·a
60 - 2·a = y - 5·a
y = 60 - 2·a + 5·a = 60 + 3·a = 60 + 3 × 8 = 84
84 - 5·a = 84 - 5 × 8 = 44
2·a + 4·a = 6·a
a + 6·a = 7·a
Please find attached the values obtained from the above evaluation of the puzzle, inputed in a similar puzzle created with MS Word.
Learn more on writing equations here: https://brainly.com/question/10892974
#SPJ1

i need help with this problem

Answers
Step-by-step explanation:
Pythagoras theorem
16²=7²+a²
a²=16²-7²
a²= 256 -49
a²=207
a=√207
a=14.38
a≈14.4 in. (approx)
Answer:
Step-by-step explanation:
As it is a right angle triangle, we can use Pythagorean theorem to find a
base² + altitude² = hypotenuse²
7² + a² = 16²
49 + a² = 256
a² = 256 - 49
a² = 207
a = √207
a = 14.4 in
You have $9.30 plus 6 percent of tax what is the total costs
Answers
Answer:
$ 9.86
Step-by-step explanation:
Tax = 6% of 9.30
= 0.06 * 9.30
= $ 0.558
Total costs = 9.30 + 0.558
= 9.858
= $ 9.86
algebra domain and range please help

Answers
Answer:
Option 2.
Step-by-step explanation:
Find the domain by finding where the function is defined. The range is the set of values that correspond with the domain.
Domain: \((- \infty} ,0)\) ∪ \((0, \infty} )\)
Range: \((- \infty} ,0)\)∪\((0, \infty} )\)
The radius of a circle is 11ft. Find its area in terms of pi
Answers
Answer: A≈380.13ft²
Step-by-step explanation:
5/12x6/15=30/180
How do I simplify?
Answers
Answer:
0.167
Step-by-step explanation:
if you divide 30/180 it will get you a decimal of 0.166666667 but if you were to divide 180 by 30 you will get 6
technecaly your answer would be 0.166666667 but you only take the first number in the decimal which is 0.1 then take six 0.16 then add the 7 0.167
that should end up being your answer if i did the math right
Answer:
Step-by-step explanation:
5/12 * 6/15 =30/180
1/6=1/6
which is true, Right-hand side is equal to left-hand side
Solve the equation x squared +6x+1=0
Answers
The solutions to the equation x² + 6x + 1 = 0 are x = -3 + 2√(2) or x = -3 - 2√(2)
What is a quadratic equation?
A quadratic equation is a second-degree polynomial equation of the form ax² + bx + c = 0 where a, b, and c are constants, and x is the variable. The solutions can be found using the quadratic formula x = (-b ± √(b² - 4ac)) / (2a) or by factoring the quadratic expression into two linear factors.
To solve the quadratic equation x² + 6x + 1 = 0, we can use the quadratic formula:
x = (-b ± √(b² - 4ac)) / (2a)
where a, b, and c are the coefficients of the quadratic equation. Substituting the values from our equation, we get:
x = (-6 ± √(6²- 4(1)(1))) / (2(1))
Simplifying inside the square root, we get:
x = (-6 ± √(32)) / 2
We can simplify the square root further by factoring out a 4:
x = (-6 ± 4√(2)) / 2
Simplifying the fraction, we get:
x = -3 ± 2√(2)
Therefore, the solutions to the equation x² + 6x + 1 = 0 are:
x = -3 + 2√(2) or x = -3 - 2√(2)
To know more about quadratic equations visit:
brainly.com/question/30098550
#SPJ1
1/5 ÷9 in it's simplest form9÷ 1/5 in it's simplest form
Answers
1/5 ÷9
= 1/5 * 1/9
= 1/45
9÷ 1/5
= 9*5/1
= 45
Zach filled 581 one-liter bottles with apple cider. He distributed the bottles to 4 stores. Each store received the same number of bottles. How many liter bottles did each of the stores receive? Were there any bottles left over?
a. 145 liter bottles (There were 2 bottles remaining)
b. 142 liter bottles (There were 2 bottles remaining)
c. 145 liter bottles (There was 1 bottle remaining)
Answers
Answer:
a. 145 liter bottles (There were 2 bottles remaining)
Step-by-step explanation:
From this question, the total number of bottles that Zach had to fill with apple cider is 581.
He has to distribute these bottles to 4 stores after filling
The question says each store received same number of bottles.
To get the number of bottles received by each store, we divide 581 by 4
= 581 / 4
= 145.25
Therefore each store gets 145 bottles each and there would be a remainder of 2 bottles
How many flowers, spaced every 6 inches, are needed to surround a circular garden with a 20-foot radius?
Answers
NEED ANSWER ASAP!!
How much water should be added to 18 mL of 15% alcohol solution to reduce the concentration to 9%?
Answers

1. The demand of calculators when its price per unit is Rs 1200,is Rs 4000. When the price increases to Rs 1500, only 3000 calculators are demanded. a.Find the demand equation in the form of p = f(Q)
b.Obtain the number of calculations demanded when the price per unit calculators is Rs 1650
c. If 4500 calculations are demanded, what should be the price per unit of calculator?
Answers
a) the demand equation in the form of p = f(Q) is p = -10/3Q + 14533.33
b) when the price per unit of calculators is Rs 1650, approximately 3865 calculators are demanded.
c) when 4500 calculators are demanded, the price per unit should be approximately Rs 3010.
To find the demand equation in the form of p = f(Q), we need to determine the relationship between the price per unit (p) and the quantity demanded (Q) based on the given information.
Let's use the two data points provided:
Point 1: Price (p1) = Rs 1200, Quantity (Q1) = 4000
Point 2: Price (p2) = Rs 1500, Quantity (Q2) = 3000
First, we calculate the slope of the demand equation using the formula:
Slope = (Q2 - Q1) / (p2 - p1)
Substituting the values, we get:
Slope = (3000 - 4000) / (1500 - 1200) = -1000 / 300 = -10/3
Next, we use one of the data points and the slope to find the y-intercept (b). Let's use Point 1:
p1 = Rs 1200, Q1 = 4000
Using the equation of a straight line (y = mx + b), we can rearrange it to solve for b:
b = y - mx
b = 1200 - (-10/3)(4000) = 1200 + 40000/3 = 1200 + 13333.33 = 14533.33
Therefore, the demand equation in the form of p = f(Q) is:
p = -10/3Q + 14533.33
To find the number of calculators demanded (Q) when the price per unit is Rs 1650, we can rearrange the equation and solve for Q:
1650 = -10/3Q + 14533.33
-10/3Q = 1650 - 14533.33
-10/3Q = -12883.33
Q = (-12883.33) / (-10/3)
Q = 12883.33 * 3/10
Q ≈ 3865
Therefore, when the price per unit of calculators is Rs 1650, approximately 3865 calculators are demanded.
Now, let's determine the price per unit (p) when 4500 calculators are demanded. We rearrange the equation and solve for p:
4500 = -10/3Q + 14533.33
-10/3Q = 4500 - 14533.33
-10/3Q = -10033.33
Q = (-10033.33) / (-10/3)
Q = 10033.33 * 3/10
Q ≈ 3010
Therefore, when 4500 calculators are demanded, the price per unit should be approximately Rs 3010.
By using the slope-intercept form of a linear equation and the given data points, we can determine the demand equation and solve for various scenarios, including finding quantities demanded at specific prices and determining the appropriate price for a given quantity demanded.
Know more about quantity here:
https://brainly.com/question/13270106
#SPJ11