What is negative four equals x divided by five plus six
Answers
Step-by-step explanation:
Negative four
-4
Equal to x
-4=x
Divided by five
-4=x/5
Plus six
-4=x/5 +6
Interpretation in the picture above
Solution
Multiply through with 5
5×-4=5×x/5 + 5×6 as shown in the second picture
-20=x+30
Collect like terms
-20-30=x
-50=x or x=-50


Related Questions
Test the series for convergence or divergence.
5/6 - 5/8 + 5/10 - 5/12 + 5/14 - . . .
Answers
We can observe that the series is an alternating series, where the terms alternate in sign. Therefore, we can use the Alternating Series Test to determine convergence or divergence. The Alternating Series Test states that if a series alternates in sign, and the absolute value of each term in the series decreases and approaches zero, then the series converges.
In this case, the absolute value of each term is 5/6, 5/8, 5/10, etc. We can see that the denominators are increasing by 2 each time, so the absolute value of each term is decreasing and approaching zero. Therefore, we can apply the Alternating Series Test.
The Alternating Series Test also states that we must check if the limit of the absolute value of the terms is zero. We have:
lim (n→∞) 5/(2n) = 0
Since the limit of the absolute value of the terms is zero, and the series alternates in sign and the absolute value of each term decreases, the series converges.
To know more about alternating series visit:
https://brainly.com/question/30400869
#SPJ11
In a particular region, 6% of the population is thought to have a certain disease. A standard diagnostic test has been found to correctly identify 91% of the people who have the disease. However, the test also incorrectly diagnoses 8% of those who do not have the disease as having the disease (in other words, the person does not have the disease but the test tells them that they do). A randomly selected person in the region is tested for the disease. (a) What is the probability the test comes back positive
Answers
Answer:
The positive predictive value ≈ 30.012%
Step-by-step explanation:
(a) The given percentage of the people in the region that have the disease, P(D) = 6% = 0.06
The percentage people correctly identified as having the disease by the standard diagnostic test = 91%
The percentage of people incorrectly identified as having the disease by the standard diagnostic test, P(T + |H) = 8%
Therefore, the sensitivity of the test, P(T + |D) = 0.91
The specificity of the test, P(T - |H) = 1 - 0.08 = 0.92
Therefore, the probability that a person is healthy, P(H) = 1 - 0.06 = 0.94
Therefore, in a population of 1,000 people, 60 people have the disease, with a sensitivity of 91%, the test will correctly pic 0.91×66 = 60.06 people correctly with the disease and 0.91 × 940 = 855.4 people without the disease
The number of non-diseased that test positive by the test is 0.08 × 1000 = 80 people which are false positives
Therefore, the number of diseased diagnosed as negative is 0.08 × 60 = 4.8
Therefore, we have;
\(\begin{array}{cccc}&Deseased&Non-diseased& Diseased + Non-diseased\\Test \ +ve&60.06&80& 140.06\\Test \ -ve&4.8&855.4&\end{array}\)
The positive predictive value = Diseased +ve/(Diseased +ve + Non-diseased +ve)
\(The \ positive \ predictive \ value = \dfrac{Diseased +ve}{Diseased +ve + Non-diseased +ve} \times 100\)
Therefore;
The positive predictive value = 60.06/(60.06 + 140.06) × 100 ≈ 30.012%
Find the component form of the vector that translates P(-3,6) to P'(-4,8) .
Answers
Vector is the quantity that has magnitude as well as direction. The component form of the vector that translates P(-3,6) to P'(-4,8) is -i + 2j.
What is vector?A vector quantity has both magnitude and direction. It is added using parallelogram law of addition.
The sum of two vector quantities is always a vector quantity.
The sum of two vector quantities can vary from their scalar difference to their scalar addition.
The given points are P(-3,6) to P'(-4,8) .
The vector component form of two points (x₁,y₁) and (x₂,y₂) is given by ,
(x₂-x₁)i + (y₂-y₁)j
Therefore, The vector component form of given points are,
(-4-(-3))i + (8-6)j
-i + 2j.
Hence "The component form of the vector that translates P(-3,6) to P'(-4,8) -i + 2j.
To learn more about vectors click on the following link
https://brainly.com/question/13322477
#SPJ1
Maria left at 2:00 P.M. for the beach and arrived at 6:00 P.M. If she drove 203 miles to the beach, what was her average speed per hour?
Answers
Answer:
50.75 speed per hour
Step-by-step explanation:
pls mark brainliest
Answer:
60 miles per hour.
Step-by-step explanation:
First, how many hours did Maria drive? ----------> 4 hours
Second, how do we find miles per hour? rate=distance divided by time
We are trying to find the rate, so we must divide 203/4. What does that equal?
203/4 equals 50.75. She drove almost 60 miles per hour.
The vertex form of the equation of a parabola is y = = 6(x-2)²-8.
What is the standard form of the equation?
A. y = 12x2 - 6x + 8
B. y = 6x2 - - 24x + 16
c. y = 6x2 - 4x + 4
O D. y = 12x2 - 12x + 16
Answers
Answer:
B. y = 6x^2 - 24x + 16.
Step-by-step explanation:
y = 6(x - 2)^2 - 8
y = 6(x^2 -4x + 4) - 8
y = 6x^2 - 24x + 24 - 8
y = 6x^2 - 24x + 16.
can someone answer this question really quick
Simplify the expression by combining like terms.
3.6x+5.9−2.2−1.7x
Enter your answer as an expression, like this: 42x+53
Answers
Answer:
\(1.9x+3.7\)
Step-by-step explanation:
\(3.6x-1.7x+5.9-2.2=1.9x+3.7\)
Help please, I really need help please

Answers
Answer:
-70
Step-by-step explanation:
As shown in the picture, you can use the formula:
1st term + common difference(desired term -1)
From what is given, we can see that the first term is -2. We are looking for the 18th term, so 18 is our desired term. Lastly, to find the common difference, we can subtract a the term before a certain term from it:
common difference = -6 - (-2) = -4
Now, we can substitute what we have:
-2 + (-4)(18 - 1)
-2 - 4(17)
-2 - 68
-70
in a random sample of 38 restaurants it was found that the mean number of employees was 12.6 with a standard deviation of 2.4 employees. find the critical value used to test the claim that the mean number of restaurant employees is less than 15 at the 1% significance level.
Answers
Critical value used to test the claim that the mean number of restaurant employees is less than 15 at the 1% significance level is - 2.431
What is standard Deviation ?The square root of the variance is used to calculate the standard deviation, a statistic that gauges a dataset's dispersion from its mean. The variation from the mean of each data point is used to determine the standard deviation, which is equal to the square root of variance.
What is mean ?It is basically the average of the given numbers.
The given data is
Sample Size = n = 38
Sample mean = X = 12.6
Sample Standard deviation = S = 2.4
= n - 1 = 38 - 1 = 37
μ₀ = μ ≥ 15
μ₁ = μ < 15 ( left tailed )
d = 0.01
Hence, Critical value = - 2,431
To learn more about Statistics, Visit :
https://brainly.com/question/29342780
#SPJ4
Write the equation of a line that is
1
parallel to the line y =1/2
X-3 and passes
through the point (4, 6)?
Answers
Answer:
y = 1/2x + 4
Step-by-step explanation:
If it's parallel, then the slope will remain the same.
To find the y-intercept, you have to plug the coordinates into the equation.
y = 1/2x + b
6 = 1/2 (4) + b
6 = 2 + b
4 = b
The blue group has 5 students, and each student in that group brought 6 folders. the green group has 6 students, and each student in that group brought 8 folders. how many pencils did they have altogether?
Answers
To find the total number of pencils the blue and green groups have altogether, the blue and green groups altogether have 78 pencils.
The blue group has 5 students, and each student brought 6 folders. Assuming each folder contains one pencil, the total number of pencils brought by the blue group is:
Blue group pencils = 5 students * 6 folders per student = 30 pencils
The green group has 6 students, and each student brought 8 folders. Following the same assumption, the total number of pencils brought by the green group is:
Green group pencils = 6 students * 8 folders per student = 48 pencils
To find the total number of pencils, we add the number of pencils from each group:
Total pencils = Blue group pencils + Green group pencils
Total pencils = 30 pencils + 48 pencils
Total pencils = 78 pencils
Therefore, the blue and green groups altogether have 78 pencils.
To learn more about pencils visit:
brainly.com/question/9991800
#SPJ11
If M is a midpoint of segment AB and AM=3x+1, if AB=20 cm what is the value of x?
Answers
Answer:
x = 3
Step-by-step explanation:
AB is the line segment and is 20 cm
Since M is the midpoint, AM = MB = 20/2 = 10
3x + 1 = 10
==> 3x = 10- 1 = 9
==> x = 9/3 = 3
Answer:
AB=20 then AM =10
now,
\(3x + 1 = 10 \\ 3x = 10 - 1 \\ 3x = 9 \\ x = 3 \)
I only got one answer for this one I don't think I'm right.
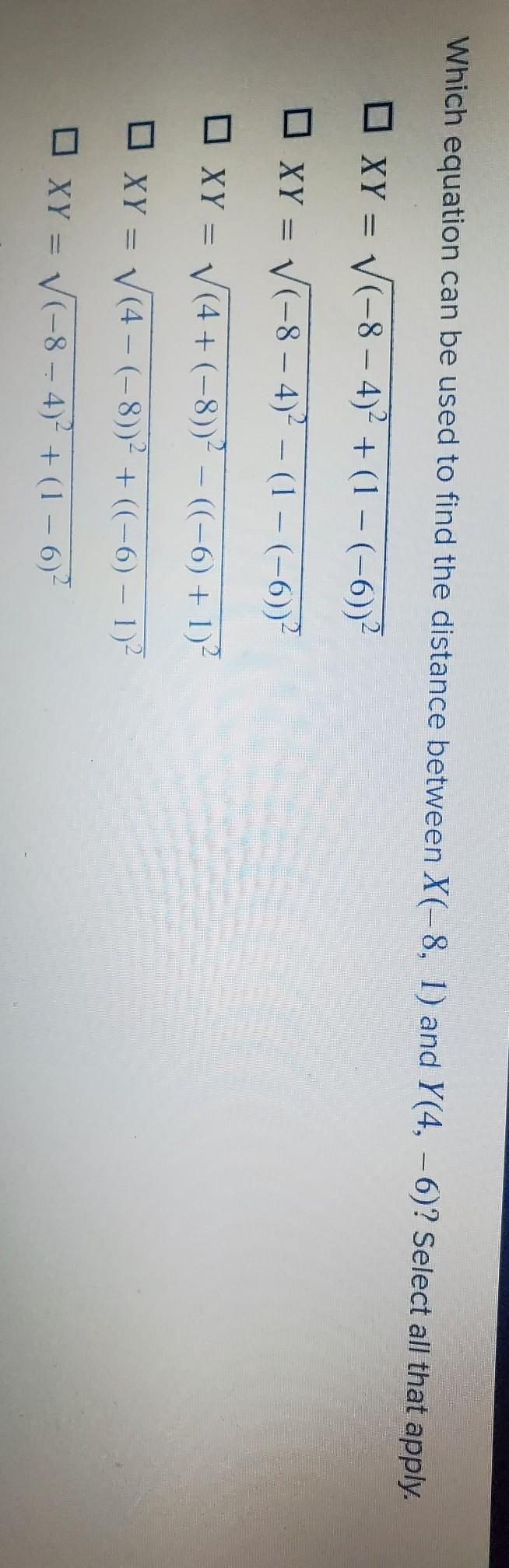
Answers
To find distance between 2 points apply Pithagoras theorem
X^2 + Y^2 = R ^ 2 for a rectangular triangle
X represents the difference between coordinates x and x'
Y represents the difference between coordinates y and y'
now find this values ( x - x') and ( y - y')
they are. (-8 -4) and ( 1 -(-6))
looking a the picture the first two options corresponds to this numbers. BUT theres a difference between them,
in the first one theres a + sign
in the 2nd one theres a - sign
the true answer is first, because Pithagoras theorem have a + sign .

correct 19784065 to 2 significant figures
Answers
Answer: 20 000 000
(the first value is two because the one after the second one (9) is greater than 5 therefore you should add 1 to the the number in front)
2.2.5a (Part 1): For the graph below, what is the x-intercept? *
-4 -2
2
-2
-4
y
2
4
0 points
X
Answers
An x-intercept is the point where the line of a graph passes through the x-axis. Thus, you should look for this point on the given graph.
What is a graph?A graph can be defined as a type of chart that is used for the graphical representation of data on both the horizontal and vertical lines of a Cartesian coordinate i.e x-axis and y-axis.
In Mathematics, x-intercept refers to the point where the line of a graph passes through the x-axis as shown in the image attached below. Since the graph wasn't provided for this question, you should look for the point where the line passes or crosses through the x-axis.
Read more on x-intercept here: https://brainly.com/question/354683
#SPJ1
• write each answer in simplest form.
1. 1/6 +2/6
2. 2/5 - 1/5
Answers
Answer:
1. 1/2
2. 1/5
Step-by-step explanation:
I used a calculator!
Answer:
1.3/6 or 1/2
2.1/5
Step-by-step explanation:
Just write that out, thats all the steps there is, 3/6 simplifies to 1/2 because they're equivalent
4. Ayla purchased two pairs of jeans for $30.50 and a shirt for $20.75. She paid with a one hundred dollar bill
How much change will Ayla get back?
851.25
$48.75
$81.75
$18.25
Answers
Answer:
i believe its $48.75
Step-by-step explanation:
I didn't know if each pair of jean was 30.50 each. I just did 30.50 + 20.75 to get 51. 25. Then i subtracted that from 100, 100- 51.25, to get 48.75
You may need to use the appropriate appendix table or technology to answer this question. The following results are for independent random samples taken from two populations. Sample 1 Sample 2 n1 = 20 n2 = 30 x1 = 22.8 x2 = 20.1 s1 = 2.2 s2 = 4.6 (a) What is the point estimate of the difference between the two population means? (Use x1 − x2. ) 2.7 (b) What is the degrees of freedom for the t distribution? (Round your answer down to the nearest integer.) (c) At 95% confidence, what is the margin of error? (Round your answer to one decimal place.) (d) What is the 95% confidence interval for the difference between the two population means? (Use x1 − x2. Round your answers to one decimal place.)
Answers
a). The difference between the two population means is estimated at a location to be 2.7.
b). 49 different possible outcomes make up the t distribution. The margin of error at 95% confidence is 1.7.
c). The range of the difference between the two population means' 95% confidence interval is (0.0, 5.4).
d). The (0.0, 5.4) represents the 95% confidence interval for the difference among the two population means.
What is standard deviations?The variability or spread in a set of data is commonly measured by the standard deviation. The deviation between the values in the data set and the mean, or average, value, is measured. A low standard deviation, for instance, denotes a tendency for data values to be close to the mean, whereas a high standard deviation denotes a larger range of data values.
Using the equation \(x_1-x_2\), we can determine the point estimate of the difference between the two population means. In this instance, we calculate the point estimate as 2.7 by taking the mean of Sample
\(1(x_1=22.8)\) and deducting it from the mean of Sample \(2(x_2=20.1)\).
With the use of the equation \(df=n_1+n_2-2\), it is possible to determine the degrees of freedom for the t distribution. In this instance, the degrees of freedom are 49 because \(n_1\) = 20 and \(n_2\) = 30.
We must apply the formula to determine the margin of error at 95% confidence \(ME=t*\sqrt[s]{n}\).
The sample standard deviation (s) is equal to the average of \(s_1\) and \(s_2\) (3.4), the t value with 95% confidence is 1.67, and n is equal to the
average of \(n_1\) and \(n_2\) (25). When these values are entered into the formula, we get \(ME=1.67*\sqrt[3.4]{25}=1.7\).
Finally, we apply the procedure to determine the 95% confidence interval for the difference between the two population means \(CI=x_1-x_2+/-ME\).
The confidence interval's bottom limit in this instance is \(x_1-x_2-ME2.7-1.7=0.0\) and the upper limit is \(x_1+x_2+ME=2.7+1.7=5.4\).
As a result, the (0.0, 5.4) represents the 95% confidence interval for the difference among the two population means.
To know more about standard deviations click-
brainly.com/question/475676
#SPJ1
Find the perimeter. Simplify your answer.
6W+7
8w-4
3w+9

Answers
(3w + 9) + (6w + 7) + (8w - 4) =
= 3w + 9 + 6w + 7 + 8w - 4 =
= 3w + 6w + 8w + 9 + 7 - 4 = 17w + 12
12/-3 Enter your answer as a number, like this: 42
Answers
Answer:
-4
Step-by-step explanation:
12/-3=-4
66 in =___ft in fraction form
Answers
Answer:66/12
Step-by-step explanation:
12 inches is one foot, so 66/12, also 66/12=5.5 feet
FIND THE ERROR Armando and Niran want to draw a trapezoid that has a height of 4 units and an area of 18 square units. Armando says that only one trapezoid will meet the criteria. Niran disagrees and thinks that she can draw several different trapezoids with a height of 4 units and an area of 18 square units. Who is correct? Explain your reasoning.
Answers
Answer:
Niran is correct.
Step-by-step explanation:
The area of a trapezoid is h(a + b)/2 where h is the height and a and b are the lengths of the opposite parallel sides.
Using the given values:
Area = 18 = 4(a + b)/2
---> 2(a + b) = 18
---> a + b = 9
Now there are many values we can assign to a and b so that they sum to 9 ( for exampl 3 and 6, 4 and 5, 1 and 8)
so Niran is correct.
Jenny went for a drive in her new car. She drove for 198.4 miles at a speed of 62 miles per hour. For how many hours did she drive?
Answers
The number of hours that Jenny drove in her new car is 3.2 hours
How to calculate the number of hours that Jenny drove in her car?
The speed is 62 miles
The distance is 198.4 miles
The number of hours can be calculated as follows
speed= distance/time
62= 198.4/x
cross multiply both sides
62x= 198.4
x= 198.4/62
x= 3.2
Hence the number of hours that Jenny drove is 3.2 hours
Read more on hours here
https://brainly.com/question/29141103
#SPJ1
A fishing boat travels along the east coast of the united states and encounters the gulf stream current. it travels 23 mi north with the current in 1 hour . it travels 30 mi south against the current in 2 hours . find the speed of the current and the speed of the boat in still water.
Answers
The speed of the boat in still water is 19 mph, and the speed of the current is 4 mph.
Let's assume the speed of the boat in still water is denoted by "B" (in mph) and the speed of the current is denoted by "C" (in mph).
When the boat is traveling north with the current, its effective speed is the sum of the speed of the boat and the speed of the current, so we can set up the equation:
(B + C) = 23/1
Similarly, when the boat is traveling south against the current, its effective speed is the difference between the speed of the boat and the speed of the current, so we have:
(B - C) = 30/2
Simplifying these equations, we get:
B + C = 23 (Equation 1)
B - C = 15 (Equation 2)
Now we can solve these equations simultaneously to find the values of B and C.
Adding Equation 1 and Equation 2, we get:
2B = 38
Dividing both sides by 2, we find:
B = 19 mph
Substituting the value of B into Equation 1, we can solve for C:
19 + C = 23
C = 23 - 19
C = 4 mph
Therefore, the speed of the boat in still water is 19 mph, and the speed of the current is 4 mph.
Learn more about speed here
https://brainly.com/question/553636
#SPJ11
combine like terms 3.26d+9.75d−2.65
Answers
3.26d + 9.75d − 2.65 = 13.01d - 2.65
3.25d +9.75d =13
So our answer is 13-2.65 because we cannot combine 2.65 because they are not like terms
Find the equation of the line through point (−5,5) and perpendicular to y=59x−4
Answers
Answer:
Step-by-step explanation:

Help ASAP ILL GIVE 10 POITNS TO ANYONE THAT WILL HELP

Answers

512 - 18 / 3
512 - 6
answer: 506
Can someone help me with this pleaseee…….

Answers
The sides of the quadrilateral arranged from longest to shortest are CD, AB, DA, and BC.
We have,
To arrange the length of the sides of the quadrilateral from longest to shortest, we need to calculate the length of each side of the quadrilateral using the distance formula:
Distance Formula:
If (x1, y1) and (x2, y2) are two points in a plane, then the distance between them is given by:
d = √((x2 - x1)² + (y2 - y1)²)
Using the distance formula, we can calculate the length of each side of the quadrilateral as follows:
AB = √((4 - (-5))² + (5 - 5)²) = 9
BC = √((2 - 4)² + (0 - 5)²) = √(29)
CD = √((-5 - 2)² + (-2 - 0)²) = √(74)
DA = √((-5 - (-5))² + (5 - (-2))²) = 7
Therefore,
The sides of the quadrilateral arranged from longest to shortest are CD, AB, DA, and BC.
Learn more about quadrilaterals here:
https://brainly.com/question/29934440
#SPJ1
what is r 156 ÷ r = 26
Answers
Answer:
r=6
Step-by-step explanation:
156/r=26
All terms are shifted to the left:
156/r-(26)=0
We divide every term by the denominator.
-26*r+156=0
All the numbers and variables are added together.
-26r+156=0
All terms containing r are shifted to the left, and all other terms are shifted to the right.
-26r=-156
r=-156/-26
r=6
What is the quotient of 0.8449 ÷ 0.71?
Answers
Answer:
1.19
Step-by-step explanation:
1) Shift the decimals of both 0.8449 and 0.71 to the right by 2 decimal places. (This is needed to convert 0.71 to 71, since long division must divide by a whole number.)
84.49 ÷ 71
2) Use the algorithm method.
1 . 1 9
7 1 | 8 4 . 4 9
7 1 .
1 3 . 4
7 . 1
6 . 3 9
6 . 3 9
3) Therefore, 0.8449 ÷ 0.71 = 1.19.
1.19
How do you find the third side of an inequality of a triangle?
Answers
To find the third side of an inequality of a triangle, you must first use the Triangle Inequality Theorem.
This theorem states that for any triangle, the sum of any two sides of the triangle must be greater than the third side. This means that in order to find the length of the third side, you must subtract the sum of the two known sides from the smaller of the two sides, then the length of the third side will be equal to the difference between these two numbers. For example, if two sides of a triangle have lengths of 4 and 3, the third side must be greater than 1 (4 + 3 = 7 and 4 - 3 = 1). Therefore, the length of the third side must be greater than 1.
Learn more about Triangle Inequality Theorem here:
https://brainly.com/question/1163433
#SPJ4