what is the answer to 6x+9=2x-7
Answers
Answer:
x= -4
Step-by-step explanation:
Answer:
x=-4
Step-by-step explanation:
6x-2x=-7-9
4x=-16
x=-16/4
x=-4
Related Questions
Aisha needs $10,000 in 5 years. How much does she need to deposit today into an account earning 2% a year in order to reach her goal? (Enter the amount POSITIVE, even if the calculator gives you a negative number, for "money leaving the pocket".)
Answers
Aisha needs to deposit $8,665.48 today to reach her goal of $10,000 in 5 years.
How to determineWhen it comes to depositing an amount in an account to achieve a particular goal in the future, the concept of present value comes into play.
Present value is the value of a future sum of money or cash flow given a specified rate of return in today's terms. In other words, it is the value of the money we deposit today that will be worth in the future.
The formula to calculate present value is given by:
Present Value = Future Value / (1 + r)ⁿ
Where r is the annual interest rate, and n is the number of years.Using this formula, we can calculate the amount Aisha needs to deposit today to achieve her goal of $10,000 in 5 years.
Assuming an annual interest rate of 2%, we have:
Present Value = $10,000 / (1 + 0.02)⁵
Present Value = $8,665.48
Learn more about deposit at
https://brainly.com/question/29454677
#SPJ11
The velocity of a particle. P. moving along the x-axis is given by the differentiable function v, where (t) is measured in meters per hour and r is measured in hours. V() is a continuous and decreasing function Selected values of v(f) are shown in the table above. Particle P is at the t= 30 at time t = 0. T(hours) 0 2 4 7 10 V(t) (meters/hour) 20.3 14.4 10 7.3 5 (a) Use a Right Riemann sum with the four subintervals indicated by the data in the table to approximate the displacement of the particle between 0 hr to 10 hr. What is the estimated position of particle Pat t=10? Indicate units of measure. (b) Does the approximation in part (a) overestimate or underestimate the displacement? Explain your reasoning (c) A second particle, Q. also moves along the x-axis so that its velocity for O<=T<= 10 is given by VQ(t) = 35✓t cos( 0.06t^2) meters per hour. Find the time interval during which the velocity of particle vo(t) is at least 60 meters per hour. Find the distance traveled by particle Q during the interval when the velocity of particle Q is at least 40 meters per hour. (d) At time t = 0, particle Q is at position x = -90. Using the result from part (a) and the function vo(t) from part (c), approximate the distance between particles P and Q at time t = 10.
Answers
The velocity of a particle. P. moving along the x-axis is given by the differentiable function v, where (t) is measured is given by:
A differential function v gives the velocity of a particle P travelling down the x-axis, where v(t) is measured in metres per hour and t is measured in hours. v(t) is a declining function that is continuous. The table below shows several examples of v(t) values.
T [hours] 0 2 4 7 10
v(t) [meters/hour] 20.3 14.4 10 7.3 5
a) We know that the particle's displacement is the area under the curve v(t). We can calculate the particle's displacement by integrating v(t). Because v(t) is a monotonous (constantly declining) differentiable function, it is also Riemann Integrable. There are now five non-uniform subdivisions:
Partition t0 t1 t2 t3 t4
T [hours] 0 2 4 7 10
v(t) [meters/hour] 20.3 14.4 10 7.3 5
Using Right Riemann sum to approximate the displacement of particle between 0 hr and 10 hr is given by:
\(\sum_{n=1}^{4}v(t_n)\Delta t_n=v(t_1)(t_1-t_0)+v(t_2)(t_2-t_1)+v(t_3)(t_3-t_2)+v(t_4)(t_4-t_3) \\=(14.4)(2)+(10)(2)+(7.3)(3)+(5)(3) \\=28.8+20+21.9+15 \\=85.7\)
Therefore, the total displacement between 0 hr and 10 hr is is 85.7 meters.
The estimated position of particle P at time t = 10 hour is 115.7 (= 30 +85.7) meters.
b) Because the function v(t) is decreasing and we are estimating the integral using the Right Riemann sum, the approximation in part(a) underestimates the displacement.
c) A second particle Q also moves along the x-axis so that its velocity is given by :
\(V_Q(t)=35\sqrt{t}\cos(0.06t^2)\text{ meters per hour for }0\leq t\leq 10.\)
Hence, the time interval during which the velocity of a particle is atleast 60 meters per hour is [9.404, 10].
Now, the time periods during which a particle's velocity is at least 40 metres per hour are [1.321,4.006] and [9.218, 10]. The distance travelled by the particle Q when its velocity is at least 40 metres per hour is then calculated. :
\(\int_{1.321}^{4.006}v_Q(t)dt+\int_{9.218}^{10}v_Q(t)dt\\\\=\int_{1.321}^{4.006}35\sqrt{t}\cos(0.06t^2)dt+\int_{9.218}^{10}35\sqrt{t}\cos(0.06t^2)dt\)
d) At time t = 0, particle Q is is at position x = -90.
We know that P is at xp = 115.7 meters.
Now, The position of Q at t = 10 hr is xq:
\(x_q=-90+\int_{0}^{10}v_Q(t)dt=-90+\int_{0}^{10}35\sqrt{t}\cos(0.06t^2)dt\)
And the distance between Q and P is given by :
\(|x_p-x_q|=|115.7-(-90+\int_{0}^{10}35\sqrt{t}\cos(0.06t^2)dt)|\)
\(\\=|205.7-\int_{0}^{10}35\sqrt{t}\cos(0.06t^2)dt|\)
Learn more about Velocity particle question:
https://brainly.com/question/14879436
#SPJ4


mina 15. a car gets $12$ miles per gallon uphill and $24$ miles per gallon downhill. if the car goes to the top of pike's peak and back ($48$ miles uphill followed by $48$ miles downhill), what is the car's gas mileage, in miles per gallon, for the entire trip?
Answers
If the car goes to the top of spike's peak and back, the mileage of the car is 16 miles per gallon
The mileage of car in uphill = 12 miles per gallon
The mileage of car in downhill = 24 miles per gallon
The total distance traveled in up hill = 48 miles
The number of gallon of gas used = 48/12
= 4 gallon
The total distance traveled in down hill = 48 miles
The number of gallon of gas used = 48 / 24
= 2 gallon
Total distance traveled = 48 + 48
= 96 miles
Total number of gallons of gas = 4 + 2
= 6 gallon
The mileage = Total distance / The number of gallon
= 96 / 6
= 16 miles per gallon
Therefore, the mileage of the car is 16 miles per gallon
Learn more about mileage here
brainly.com/question/3124860
#SPJ4
This table contains equivalent ratios between x and y
——————-
x
1
3
7
——————-
y
5
15
25
35
Answers
The missing values in the table that contains the equivalent ratios between X and Y would be = 5
What is an equivalent ratio?An equivalent ratio is defined as the constant that exists between two different numbers when compared.
The figures in the table is as follows:
X= 1 3 ? 7
y = 5 15 25 35
If X = 1 when y = 5, X= ? when y= 25
That is;
1 =5
?= 25
? = 25/5 = 5
Learn more about ratio here:
https://brainly.com/question/29145263
#SPJ1
Subtract using a number line.
−2.9−(−0.6)
Plot the minuend and the difference on the number line. if you answer it can you put it on the number line please because i get the answers right but i put them in the wrong place
Answers
Answer: -2.7 and -2.3 are your answers
on the number line: 2 dots behind -2.5 and 2 dots forward
The difference between the numbers -2.9 and -0.6 is -2.3 after using the number line.
What is a number line?It is defined as the representation of the numbers on a straight line that goes infinitely on both sides.
It is given that:
As we can see in the number line:
If we take the difference between these two numbers
From the number line:
= −2.9−(−0.6)
= -2.9 + 0.6
= -2.3
The arithmetic operation can be defined as the operation in which we do the addition of numbers, subtraction, multiplication, and division. It has a basic four operators that is +, -, ×, and ÷.
After using the arithmetic operation concept:
The difference between the numbers:
= −2.9−(−0.6)
= -2.9 + 0.6
= -2.3
Thus, the difference between the numbers -2.9 and -0.6 is -2.3 after using the number line.
Learn more about the number line here:
brainly.com/question/13189025
#SPJ2

The second sail has one side of length 22 feet and another of length 2 feet. Determine the range of possible lengths of the third side of the sail.
Answers
Answer:
20 < L < 24
Step-by-step explanation:
We know that in any given triangle, the length of two sides is always greater than the length of the third side.
Since the sail is a triangle having length of one side as 22 feet and the length of another side as 2 feet, and let L be the length of the third side.
It follows from our triangle rule of sides above that
22 + 2 > L (1)
22 + L > 2 (2)and
L + 2 > 22 (3)
It follows that from (1)
22 + 2 > L
⇒ 24 > L (4)
It follows that from (2)
22 + L > 2
⇒ L > 2 - 22
⇒ L > - 44 (5) and
It follows that from (3)
L + 2 > 22
⇒ L > 22 - 2
⇒ L > 20 (6)
Since from (5) and (6),
L > -44 and L > 20
and 20 > -44 ⇒ L > 20
⇒ 20 < L (7)
From (4) 24 > L ⇒ L < 24 (8)
Combining (7) and (8), we have
20 < L < 24
So, the possible range of values of the third side are 20 < L < 24
Find the gradients of lines a and b

Answers
Answer:
Line A = y = 8x – 6
Line B = y = -4x + 8
Step-by-step explanation:
please help and answer the following proof! WIll give brainliest

Answers
The proof for UX || VW is shown below.
What is Mid point Theorem?According to the midpoint theorem, "The line segment in a triangle joining the midpoint of any two of the triangle's sides is said to be parallel to its third side and is also half the length of the third side."
Given:
As, TUX and TVW are similar.
So, the ratio of their corresponding sides are equal.
So, TU/ TV = UX/ VW = TX / TW = 1/2 {TU/ TV = 1/2}
By using mid point Theorem
UX = 1/2 VW
Then, UX || VW.
Learn more about Mid- point theorem here:
https://brainly.com/question/13677972
#SPJ1
Make the following conversion. 4mm = _____ cm 0.04 0.4 40 400
Answers
Answer:
0.4 cm
Step-by-step explanation:
10 mm = 1 cm thus 4mm / 10 = 0.4 cm
The radius of a circle is 21 m. Find its area to the nearest whole number.
Answers
Answer: A≈1385.44m²
Step-by-step explanation:
A=πr2=π·212≈1385.44236m²
21 x 21 = 441
441 x pi = 1385.44
Área = 1385.44
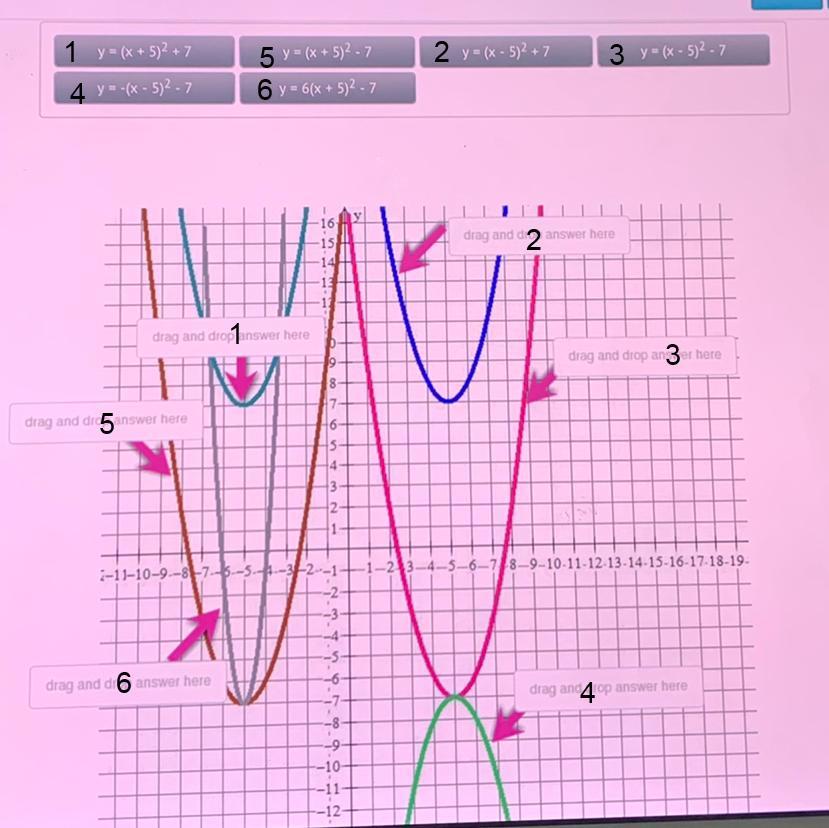
in the some important for of the image below about , some have more details available when you click on them Drag and drop each corresponding area it identities in the image

Answers
Vertex Form of a quadratic equation
A quadratic equation has the vertex form:
\(y=a(x-h)^2+k\)Where (h,k) is the vertex of the parabola and a is the leading coefficient.
If a is positive, the parabola is concave up, if a is negative, the parabola is concave down.
We'll identify each graph with a number so we can relate them with their corresponding equation.
Graph 1. Has the vertex at (-5,7) and opens up. The equation of this parabola (for a=1) is:
\(y=(x+5)^2+7\)Graph 2 has the vertex at (5,7) and opens up. The equation is:
\(y=(x-5)^2+7\)Graph 3 has the vertex at (5,-7) and opens up. The equation is
\(y=(x-5)^2-7\)Graph 4 has the vertex at (5,-7) and opens down. The equation is
\(y=-(x-5)^2-7\)Graph 5 has the vertex at (-5,-7) and opens up. The equation is
\(y=(x+5)^2-7\)Finally, graph 6 has the same vertex as graph 5 and opens up also, but it grows much faster than that one. The difference is that the leading factor is greater than one. This corresponds to the equation
\(y=6(x+5)^2-7\)The image below shows the correspondence between the graphs and their equations labeled with numbers.
How tall is a building that casts a 20 foot shadow if the angle of elevation from the ground to the top of the building is 43∘ ?
Answers
To determine the height of the building, we can use trigonometry. In this case, we can use the tangent function, which relates the angle of elevation to the height and shadow of the object.
The tangent of an angle is equal to the ratio of the opposite side to the adjacent side. In this scenario:
tan(angle of elevation) = height of building / shadow length
We are given the angle of elevation (43 degrees) and the length of the shadow (20 feet). Let's substitute these values into the equation:
tan(43 degrees) = height of building / 20 feet
To find the height of the building, we need to isolate it on one side of the equation. We can do this by multiplying both sides of the equation by 20 feet:
20 feet * tan(43 degrees) = height of building
Now we can calculate the height of the building using a calculator:
Height of building = 20 feet * tan(43 degrees) ≈ 20 feet * 0.9205 ≈ 18.41 feet
Therefore, the height of the building that casts a 20-foot shadow with an angle of elevation of 43 degrees is approximately 18.41 feet.
Learn more about probability here
brainly.com/question/13604758
#SPJ11
add: 8x^2+7xy-6y^2, 4x^2-3xy+2y^2 and -4x^2+xy-y^2
Answers
Answer:
8x² - 5y² + 5xy
Step-by-step explanation:
8x² + 7xy - 6y² + 4x² - 3xy + 2y² - 4x² + xy - y² = (8x² + 4x² -4x²) + (-6y² + 2y² - y²) + (7xy - 3xy + xy) = 8x² - 5y² + 5xy
The area of a rectangular room is 750 square feet. The width of the room is 5 feet less than the length of the room. Which equations can be used to solve for y, the length of the room? Select three options. y(y + 5) = 750 y2 – 5y = 750 750 – y(y – 5) = 0 y(y – 5) + 750 = 0 (y + 25)(y – 30) = 0
Answers
y2 – 5y = 750
750 – y(y – 5) = 0
(y + 25)(y – 30) = 0
consider the first two terms of this sequence 1/16, -3/16 Determine the 63rd term if this is an arithmetic sequence. Write your answer as a reduced improper fraction. Determine the 63rd term if this is a geometric sequence. Write your answer in scientific notation.
Answers
The 63rd term is \(-\frac{247}{16}\) if it is an arithmetic sequence.
The 63rd term is \(2.385\times 10^{28}\) if it is an geometric sequence.
An arithmetic sequence has the characteristic that the difference between two consecutive elements is the same, that is to say:
\(a_{i+1}-a_{i} = r\) (1)
The expression that represents the elements of the arithmetic sequence is presented below:
\(a(n) = a_{1} + r\cdot (n-1)\) (2)
Where:
\(n\) - Index of the element of the sequence.\(r\) - Increase rate.\(a_{1}\) - First element of the arithmetic sequence.If we know that \(a_{1} = \frac{1}{16}\), \(a_{2} = -\frac{3}{16}\) and \(n = 63\), then the 63rd term of the arithmetic sequence:
\(r = -\frac{3}{16}-\frac{1}{16}\)
\(r = -\frac{1}{4}\)
\(a(63) = \frac{1}{16}-\frac{1}{4}\cdot (63-1)\)
\(a(63) = -\frac{247}{16}\)
The 63rd term is \(-\frac{247}{16}\) if it is an arithmetic sequence.
An geometric sequence has the characteristic that the ratio between two consecutive elements is the same, that is to say:
\(\frac{a_{i+1}}{a_{i}} = r\) (3)
The expression that represents the elements of the geometric sequence is presented below:
\(a(n) = a_{1}\cdot r^{n-1}\) (4)
Where:
\(n\) - Index of the element of the sequence.\(r\) - Increase rate.\(a_{1}\) - First element of the arithmetic sequence.If we know that \(a_{1} = \frac{1}{16}\), \(a_{2} = -\frac{3}{16}\) and \(n = 63\), then the 63rd term of the arithmetic sequence:
\(r = \frac{-\frac{3}{16} }{\frac{1}{16} }\)
\(r = -3\)
\(a (63) = \left(\frac{1}{16} \right)\cdot (-3)^{63-1}\)
\(a(63) = 2.385\times 10^{28}\)
The 63rd term is \(2.385\times 10^{28}\) if it is an geometric sequence.
We kindly invite to see this question on geometric sequence: https://brainly.com/question/11266123
When a scientist conducted a genetics experiments with peas, one sample of offspring consisted of 943 peas, with 715 of them having red flowers. If we assume, as the scientist did, that under these circumstances, there is a 3/4 probability that a pea will have a red flower, we would expect that 707.25 (or about 707) of the peas would have red flowers, so the result of 715 peas with red flowers is more than expected.
a. If the scientist's assumed probability is correct, find the probability of getting 715 or more peas with red flowers.
b. Is 715 peas with red flowers significantly high?
c. What do these results suggest about the scientist's assumption that 3/4 of peas will have red flowers?
Answers
Using the normal approximation to the binomial distribution, it is found that:
a) 0.454 = 45.4% probability of getting 715 or more peas with red flowers.
b) Since Z < 2, 715 peas with red flowers is not significantly high.
c) Since 715 peas with red flowers is not a significantly high result, we cannot conclude that the scientist's assumption is wrong.
For each pea, there are only two possible outcomes. Either they have a red flower, or they do not. The probability of a pea having a red flower is independent of any other pea, which means that the binomial distribution is used to solve this question.
Binomial distribution:Probability of x successes on n trials, with p probability.
Normal distribution:The z-score of a measure X in a normal distribution with mean and standard deviation is given by:
\(z=\frac{X-mean}{standard deviation}\)
If Z > 2, the result is considered significantly high.
In this problem:
943 peas, thus, n=943
3/4 probability of being red, thus . p=\(\frac{3}{4} =0.75\)
Applying the approximation:
mean = np= 943x0.75 = 707.25
standard deviation = \(\sqrt{np(1-p)} = \sqrt{707.25*0.25} = 13.297\)
a):
Using continuity correction, this probability is
P(X\(\geq\)715-0.5)=P(X\(\geq\)714.5), which is 1 subtracted by the p-value of Z when X = 714.5.
Then:
\(Z=\frac{X-mean}{standard deviation} \\\\Z=\frac{714.5-707.25}{13.297} \\\\Z=0.5452\)
now , 1- 0.5452=0.454
0.454= 45.4% probability of getting 715 or more peas with red flowers.
b):
Since Z < 2, 715 peas with red flowers is not significantly high.
c):
Since 715 peas with red flowers is not a significantly high result, we cannot conclude that the scientist's assumption is wrong.
Learn more about binomial distribution, visit:
brainly.com/question/25212369
#SPJ1
5x - 4y = -10
y = 2x - 5
2 =
y =

Answers
Answer:
x=10
y=15
Step-by-step explanation:
Since we know y in terms of x, we can use substitution and say instead of-
5x-4y=-10
5x-4(2x-5)=-10
5x-8x+20=-10
-3x=-30
x=10
Substitute x into the equation-
y=2x-5
y=2(10)-5
y=20-5=15.
If an orthocenter lies inside of a triangle, then the triangle must be
isosceles.
obtuse.
right.
acute.
Answers
Answer:
acuteStep-by-step explanation:
Remember :the orthocenter of a triangle is the point of concurrency of the 3 altitudes.
\(\large \text{If an orthocenter lies inside of a triangle, then the triangle must be}\ :\\\\\large isosceles. \\\\\large obtuse. \\\\\large right. \\\\\large acute \checkmark\)
If an orthocenter lies inside of a triangle, then the triangle must be acute.
What is Triangle?A triangle is a three-sided polygon that consists of three edges and three vertices.
Orthocenter of a triangle is the intersection of any two of three altitudes of a triangle.
The third altitude usually pass through the point of the first two altitudes.
When the orthocenter lies inside a triangle, the angles formed by the intersection of the three altitudes is less than 90 degrees.
An acute triangle is a type of triangle whose angles are less than 90 degrees.
Hence, If an orthocenter lies inside of a triangle, then the triangle must be acute.
To learn more on Triangles click:
https://brainly.com/question/2773823
#SPJ7
find the area of the region that lies inside the first curve and outside the second curve. r = 5 − 5 sin(), r = 5
Answers
The area of the region is (25/4)π + 50 square units.
How to find the area of the region that lies inside the first curve and outside the second curve?The given equations are in polar coordinates. The first curve is defined by the equation r = 5 − 5 sin(θ) and the second curve is defined by the equation r = 5.
To find the area of the region that lies inside the first curve and outside the second curve, we need to integrate the area of small sectors between two consecutive values of θ, from the starting value of θ to the ending value of θ.
The starting value of θ is 0, and the ending value of θ is π.
The area of a small sector with an angle of dθ is approximately equal to (1/2) r² dθ. Therefore, the area of the region can be calculated as follows:
Area = 1/2 ∫[0,π] (r1²- r2²) dθ, where r1 = 5 − 5 sin(θ) and r2 = 5.Area = 1/2 ∫[0,π] [(5 − 5 sin(θ))² - 5^2] dθArea = 1/2 ∫[0,π] [25 - 50 sin(θ) + 25 sin²(θ) - 25] dθArea = 1/2 ∫[0,π] [25 sin²(θ) - 50 sin(θ)] dθArea = 1/2 [25/2 (θ - sin(θ) cos(θ)) - 50 cos(θ)] [0,π]Area = 1/2 [(25/2 (π - 0)) - (25/2 (0 - 0)) - 50(-1 - 1)]Area = 1/2 [(25/2 π) + 100]Area = (25/4) π + 50Therefore, the area of the region that lies inside the first curve and outside the second curve is (25/4) π + 50 square units.
Learn more about area of the region
brainly.com/question/28334840
#SPJ11
f(x+h)-f(x)/h difference quotient h for the function given below. f(x) = -8x +9 simplified expression involving and h, if necessary. For example, if you found that the difference quotient was - you would enter x + h. de your answer below:
Answers
Therefore, the answer is -8. The simplified expression involving h is -8. The difference quotient is the formula used in calculus to compute the derivative of a function.
The given function is f(x) = -8x +9.The difference quotient h for the given function is calculated as follows: f(x+h)-f(x) / hf(x+h) = -8(x+h) + 9 = -8x - 8h + 9f(x) = -8x + 9
So, the numerator is given by: f (x+h) - f(x) = [-8 ( x+h) + 9] - [-8x + 9]= -8x - 8h + 9 + 8x - 9= -8h
On substituting the numerator and denominator values in the given equation we have:(-8h) / h= -8
Therefore, the answer is -8.
The simplified expression involving h is -8. The difference quotient is the formula used in calculus to compute the derivative of a function.
The quotient formula is used to calculate the average rate of change in a function, with h representing the change in the input variable x.
The difference quotient formula is also used to calculate the slope of a curve at a given point.
To know more about Expression visit :
https://brainly.com/question/28172855
#SPJ11
. Determine the instantaneous rate of change at x=−1. b. Determine the average rate of change on the interval −1≤x≤2
Answers
a.) The instantaneous rate of change at x = -1 for the function f(x) = 2x² - 3x + 1 is -7.
b.) The average rate of change on the interval [-1, 2] for the function f(x) = 2x² - 3x + 1 is -4/3.
a)
Instantaneous rate of change of a function can be defined as the rate of change of a function at a particular point.
It is also called the derivative of a function.
The instantaneous rate of change at x = -1 is given by:
f'(-1) = (d/dx) f(x)|x=-1
Given the function f(x) = 2x² - 3x + 1,
Using the power rule of differentiation, we get
f'(x) = d/dx (2x² - 3x + 1) = 4x - 3 At x = -1,
we have f'(-1) = 4(-1) - 3 = -7
Therefore, the instantaneous rate of change at x = -1 is -7.
b)
The average rate of change of a function over a given interval [a, b] is the ratio of the change in y-values (Δy) to the change in x-values (Δx) over the interval. It is given by:
(f(b) - f(a))/(b - a)
For the function f(x) = 2x² - 3x + 1,
evaluate (f(2) - f(-1))/(2 - (-1)) = (8 - 12)/(3) = -4/3
Therefore, the average rate of change on the interval [-1, 2] is -4/3.
To know more about instantaneous rate of change visit:
https://brainly.com/question/30760748
#SPJ11
This is due like now!!!! Please help!!!
Look at the graph:
What is the slope?
Simplify your answer and write it as a proper fraction, improper fraction, or integer.

Answers
Which pair of quantities is LEAST likely to be directly proportional?.
Answers
Answer:
Hours worked and money earned
Distance and time when speed is constant
Area and side length of a square
Total cost and the number of hats purchased
Step-by-step explanation:
18. Which prize is worth more? Explain your
reasoning
a prize on March 31, if the amount is
tripled each day, beginning with $3 on
March 1
• a prize after 50 years, if $1 million is
added each day
Answers
The highest prize will be that of 50 years of duration, while it will generate $ 18,262,500,000 compared to $ 3,221,225,472 of the one-month duration.
To determine which prize is worth more enter a prize on March 31, if the amount is tripled each day, beginning with $ 3 on March 1; and a prize after 50 years, if $ 1 million is added each day, the following calculations must be performed:
50 x 365.25 = 18,262.5 18,262.5 x 1,000,000 = X X = 18,262,500,000
3 x 2 ^ 30 = X 3 x 1,073,741,824 = X X = 3,221,225,472
Therefore, the highest prize will be that of 50 years of duration, while it will generate $ 18,262,500,000 compared to $ 3,221,225,472 of the one-month duration.
Learn more in https://brainly.com/question/1349797
a) A)-(-8)-(-9)
b) 9+(-6)+(7)
c) -2-3-5
d) 10-(-7)-(-8)
e) -(3)+(-8)+(1)
f) (-4)-(-6)+(-5)
por favor me urgen
Answers
Answer: what is the question
Step-by-step explanation:
When President Kimball challenged regional representatives as well as other Church members to prepare themselves for missionary service by learning the languages of the world, what language did Russell and Dantzel Nelson immediately start studying
Answers
Russell and Dantzel Nelson immediately started studying Mandarin Chinese.
This information is specific to Russell and Dantzel Nelson and their personal response to President Kimball's challenge. It is not mentioned in the question why they chose Mandarin Chinese specifically, but it can be assumed that they had their own reasons for selecting that language. It is worth noting that Mandarin Chinese is one of the most widely spoken languages in the world, and learning it would have been beneficial for missionary work in areas where Mandarin is spoken. Russell M. Nelson, who later became the President of The Church of Jesus Christ of Latter-day Saints, had significant international experience and worked extensively with various cultures and interest, further emphasizing the importance of language learning for missionary service.
Learn more about interest here:
https://brainly.com/question/30955042
#SPJ11
PLEASE HELP ME ITS URGENT!!!!
A rectangular garden has a walkway around it. The area of the garden is 4(5.5x + 1.5). The combined
area of the garden and the walkway is 4.5(8x + 4). Find the area of the walkway around the garden as
the sum of two terms.
CD
The area of the walkway around the garden is 1
(Simplify your answer. Use integers or decimals for any numbers in the expression.)
Answers
We're given:
Area (garden) = 4(5.5x + 1.5)Area (garden + walkway) = 4.5(8x + 4)To find the area of the garden alone, we can subtract the area of the garden from the combined area of the garden and walkway:
\(4.5(8x + 4)-4(5.5x + 1.5)\)
Open up the parentheses:
\(= 36x +18 -22x - 6\)
Combine like terms:
\(= 36x +18 -22x - 6\\= 14x +18 - 6\\= 14x +12\)
AnswerThe area of the walkway around the garden is 14x + 12.
WILL GIVE BRAINLIEST
The Coriolis Effect shows us that when moving from the equator towards the poles, the air is __________.
Question 1 options:
moving faster than the ground below it.
standing still.
moving at the same speed.
moving slower than the ground below it.
Answers
Answer:
answer A
Step-by-step explanation:
Option C is correct, the Coriolis Effect shows us that when moving from the equator towards the poles, the air is moving at the same speed.
What is Speed?Speed is the time rate at which an object is moving along a path,
The Coriolis Effect causes moving objects, including air, to be deflected to the right in the Northern Hemisphere and to the left in the Southern Hemisphere.
As air moves from the equator towards the poles, it experiences a change in latitude, which causes it to be deflected.
This deflection results in the formation of high-pressure and low pressure systems that move weather patterns around the globe.
The speed of the air is affected by a number of factors, including temperature, pressure, and the Coriolis Effect.
However, the Coriolis Effect does not directly affect the speed of the air as it moves from the equator towards the poles.
Therefore, the Coriolis Effect shows us that when moving from the equator towards the poles, the air is moving at the same speed.
To learn more on Speed click:
https://brainly.com/question/28224010
#SPJ2
Paula Pidcoe is doing her budget. She discovers that the average miscellaneous expense is $65.00 with a standard deviation of $18.00. What percent of her expenses in this category would she expect to fall between $54.20 and $86.60?
The z for $54.20 = -
The percent of area associated with $54.20 =
%
The z for $86.60 =
The percent of area associated with $86.60 =
%
Adding the two together, the percent of his expenses between $54.20 and $86.60 is
%
Answers
Using the normal distribution, it is found that:
The percent of area associated with $54.20 is of: 27.43%.The percent of area associated with $86.60 is of: 88.49%.Adding the two together, the percent of his expenses between $54.20 and $86.60 is of: 61.06%.Normal Probability DistributionThe z-score of a measure X of a normally distributed variable with mean \(\mu\) and standard deviation \(\sigma\) is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The z-score measures how many standard deviations the measure is above or below the mean. Looking at the z-score table, the p-value associated with this z-score is found, which is the percentile of X.The mean and the standard deviation are given, respectively, by:
\(\mu = 65, \sigma = 18\)
We find the percentage for each measure(the p-value of Z when X = measure), then subtract them.
X = 86.6:
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{86.6 - 65}{18}\)
Z = 1.2
Z = 1.2 has a p-value of 0.8849 = 88.49%.
X = 54.2:
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{54.2 - 65}{18}\)
Z = -0.6
Z = -0.6 has a p-value of 0.2743 = 27.43%.
88.49 - 27.43 = 61.06%.
More can be learned about the normal distribution at https://brainly.com/question/24537145
#SPJ1
Calculate the slope of a line that passes through the points (3, -20) and (5, 8).
6
14
26
4
Answers
Answer:
14
Step-by-step explanation:
Use rise over run, (y2 - y1) / (x2 - x1)
Plug in the points:
(y2 - y1) / (x2 - x1)
(8 + 20) / (5 - 3)
28 / 2
= 14
So, the slope is 14.