what is the area of the parallelogram in square centimeters? show your work
Answers
The area of parallelogram is Base(B) × Height(H).
The quantity of square units that make up a polygon determines its area. Similar to a carpet or area rug, area is two dimensional.
A parallelogram is a four-sided structure made up of two parallel line pairs. The length of opposing sides and the magnitude of opposing angles are both equal. Multiply the base by the height to determine the area. The equation is:
A = B × H,
where B stands for base
H for height
A parallelogram must have a perpendicular base and height. A parallelogram's lateral sides aren't parallel to the base, though. As a result, the height is represented by a dotted line. Let's examine a few instances when the area of a parallelogram is involved.
To learn more about area of parallelogram from given link
https://brainly.com/question/10744696
#SPJ9
Related Questions
I do not know this answer
i need the u answer

Answers
Utility workers need to reach the roof of a 32 foot building by using an
extended ladder. The ladder can extend to 40 feet. What angle of elevation
do the workers need place the ladder so that the top reaches the building's
roof line?
Answers
The angle of elevation of the worker is 48.6°
What is angle of elevation?The angle of elevation is an angle that is formed between the horizontal line and the line of sight. If the line of sight is upward from the horizontal line, then the angle formed is an angle of elevation.
In this scenario, the ladder and the building will at an angle (phi).
The height of the building is the opposite to the angle and the slant height of the ladder is the hypotenuse.
Therefore:
Sin(phi) = opposite/hypotenuse
sin(phi) = 30/40
phi = sin^-1(0.75)
phi = 48.6°
Therefore for the ladder to reach the top of the building l, the angle of elevation must be 48.6°
learn more about angle of elevation from
https://brainly.com/question/88158
#SPJ1
Write 10 1/3 as an improper fraction
Answers
Answer:
31/3
Step-by-step explanation:
The 10 1/3 written as the improper fraction 31/3.
To convert the mixed number 10 1/3 into an improper fraction, follow these steps:
Multiply the whole number (10) by the denominator of the fraction (3):
10 × 3 = 30
Add the result from step 1 to the numerator of the fraction (1):
30 + 1 = 31
Place the result from step 2 over the original denominator (3) to form the improper fraction:
10 1/3 = 31/3
To know more about fraction here
https://brainly.com/question/10354322
#SPJ6
if a rivet passes through two sheets of metal, each 1/16 of an inch thick, and has a shank of 1/4 inch, what length should the rivet be?
Answers
The length of the rivet should be 3/8 inch to pass through the two sheets of metal.
To solve this problemWe must take into account the shank length as well as the thickness of the two metal sheets.
Assumed:
Each sheet of metal has a thickness of 1/16 inch14 inch for the shank lengthThe thickness of the two metal sheets and the shank length must be added to determine the overall length of the rivet:
Total length = 2 * (Thickness of sheet metal) + Shank length
Substituting the values:
Total length = 2 * (1/16 inch) + 1/4 inch
Calculating the values:
Total length = 1/8 inch + 1/4 inch
Total length = 1/8 inch + 2/8 inch
Total length = 3/8 inch
So, the length of the rivet should be 3/8 inch to pass through the two sheets of metal.
Learn more about Substituting here : brainly.com/question/26094713
#SPJ4
Kira is trying to drink more water and juice each day. The difference in the amount of water in a jug and the amount of juice in the bottle she is drinking from is 192 ounces. She has consumed a total of 42 ounces, which is StartFraction 3 Over 32 EndFraction of the bottle of juice and StartFraction 9 Over 64 EndFraction of the jug of water. Which system of equations can be used to determine the total number of ounces in the jug of water, x, and the total number of ounces in the bottle of juice, y? x minus y = 192 and StartFraction 9 Over 64 EndFraction x StartFraction 3 Over 32 EndFraction y = 42 x minus y = 192 and StartFraction 3 Over 32 EndFraction x StartFraction 9 Over 64 EndFraction y = 42 x y = 192 and StartFraction 9 Over 64 EndFraction x StartFraction 3 Over 32 EndFraction y = 42 x y = 192 and StartFraction 3 Over 32 EndFraction x StartFraction 9 Over 64 EndFraction y = 42.
Answers
Answer:
A. x-y=192 and 9/64x+3/32y=42
Step-by-step explanation:
i got it right dw
You split $2200 between two savings accounts. account a pays an annual interest rate of 5% and account b pays an annual interest rate of 3%. after one year, you have earned a total of $78.50 in interest. how much money did you invest in each account?
Answers
Answer:
$625 at 5%$1575 at 3%Step-by-step explanation:
Let x be the amount at 5%
Then 2200 - x is the amount at 3%
The total interest is:
0.05x + (2200 - x)*0.03 = 78.505x + (2200 - x)*3 = 78505x + 6600 - 3x = 78502x = 7850 - 66002x = 1250x = 625Find the amount at 3%:
2200 - 625 = 1575Find the optimal values of x and y using the graphical solution method: Min x + y subject to: x + y ≥ 7 5x + 2y ≥ 20 x ≥ 0, y ≥ 0.
Answers
The optimal values of x and y that minimize the objective-function x + y, subject to the given constraints, are x = 4 and y = 0.
We can find the corner points of the feasible region and evaluate the objective function at those points to determine the optimal solution.
Graph the constraints:
Start by graphing the inequalities:
x + y ≥ 7
5x + 2y ≥ 20
x ≥ 0
y ≥ 0
Plot the lines x + y = 7 and 5x + 2y = 20. To graph x + y = 7, plot two points that satisfy the equation, such as (0, 7) and (7, 0), and draw a line through them. To graph 5x + 2y = 20, plot two points such as (0, 10) and (4, 0), and draw a line through them.
Shade the region that satisfies the inequalities x ≥ 0 and y ≥ 0.
The feasible region will be the shaded region.
Identify the feasible region:
The feasible region is the shaded region where all the constraints are satisfied. In this case, the feasible region will be a polygon bounded by the lines x + y = 7, 5x + 2y = 20, x = 0, and y = 0.
Find the corner points:
Locate the intersection points of the lines and the axes within the feasible region. These are the corner points. In this case, we have the following corner points:
Intersection of x + y = 7 and x = 0: (0, 7)
Intersection of x + y = 7 and y = 0: (7, 0)
Intersection of 5x + 2y = 20 and x = 0: (0, 10)
Intersection of 5x + 2y = 20 and y = 0: (4, 0)
Evaluate the objective function:
Evaluate the objective function, which is x + y, at each corner point:
(0, 7): x + y = 0 + 7 = 7
(7, 0): x + y = 7 + 0 = 7
(0, 10): x + y = 0 + 10 = 10
(4, 0): x + y = 4 + 0 = 4
Determine the optimal solution:
The optimal solution is the corner point that minimizes the objective function (x + y). In this case, the optimal solution is (4, 0) because it has the smallest objective function value of 4.
Therefore, the optimal values of x and y that minimize the objective function x + y, subject to the given constraints, are x = 4 and y = 0.
Learn more about objective function from the given link
https://brainly.com/question/26100401
#SPJ11
The same front hit Pittsburgh the next morning. The temperature dropped by 8°F each hour from 5:00 a.M. To 9:00 a.M.. If the temperature at 9:00 a.M. Was -5°F what was the beginning temperature at 5:00 a.M.? There are different ways to solve a problem. Claire and Dan solved this problem differently. Dan said his method involved multiplication, while Claire said she did not use multiplication. Both students arrived at the correct answer. How is this possible? Explain. What answer did they both arrive at?
Answers
Answer:
The beginning temperature at 5:00 a.M was 27°F
The answer they both arrived at was 27°F
Step-by-step explanation:
From the question,
The temperature dropped by 8°F each hour from 5:00 a.M. To 9:00 a.M.
From 5:00 a.M to 9:00 a.M, there are 4 hours.
Hence, the temperature dropped by 8°F each hour for 4 hours.
Also, from the question
The temperature at 9:00 a.M. was -5°F,
To determine the beginning temperature at 5:00 a.M,
Let the beginning temperature be x
For Dan's method, his method involved multiplication, He could have done it this way:
Since the temperature dropped by 8°F each hour for 4 hours,
This means the temperature would have reduced by 4 × 8°F = 32°F
Now, we can write that
x - 32°F = -5°F
Then, x = -5°F + 32°F
x = 27°F
For Claire's method, she did not use multiplication, she could have done it step-wisely, reducing the temperature by 8°F every hour.
Since the temperature dropped by 8°F each hour from 5:00 a.M. To 9:00 a.M,
Let the beginning temperature be x
After 1 hour, that is at 6:00 a.M, the temperature will be x - 8°F
After 2 hours, that is at 7:00 a.M, the temperature will be x - 8°F - 8°F = x -16°F
After 3 hours, that is at 8:00 a.M, the temperature will be x -16°F - 8°F = x -24°F
After 4 hours, that is at 9:00 a.M, the temperature will be x -24°F - 8°F = x -32°F
From the question, the temperature at 9:00 a.M. was -5°F
Hence,
x -32°F = -5°F
Then,
x = -5°F + 32°F
x = 27°F
Hence, the answer they both arrived at was 27°F.
please help!
Megan has a bag with 8 red cubes, 3 yellow cubes, and 5 green cubes. What is the probability she will pick a red cube, keep it, and then pick another red cube?
Answers
Answer:
1st time: 50% chance or 8/16 chance
2nd time: 46% chance or 7/15
I can try again if its wrong
Answer:
7/30
Step-by-step explanation:
8/16 that she picks a red cube.
7/15 that she picks another red cube after keeping the first red cube.
multiply 8/16 (1/2) times 7/15 to get 7/30 as your final answer
determine whether the series is convergent or divergent. [infinity] k = 1 ke−k2
Answers
Answer:
Convergent
Step-by-step explanation:
One method to determine if \(\displaystyle \sum^\infty_{k=1}ke^{-k^2}\)is convergent or divergent is the Integral Test.
Suppose that the function we use is \(f(x)=xe^{-x^2}\). Over the interval \([1,\infty)\), the function is always positive and continuous, but we also need to make sure it is decreasing before we can proceed with the Integral Test.
The derivative of this function is \(f'(x) = e^{-x^2}(1-2x^2)\), so our critical points will be \(\displaystyle x=\pm\frac{1}{\sqrt{2}}\), but we can drop the negative critical point as we are starting at \(k=1\). Using some test points, we can see that the function increases on the interval \(\bigr[0,\frac{1}{\sqrt{2}}\bigr]\) and decreases on the interval \(\bigr[\frac{1}{\sqrt{2}},\infty\bigr)\). Since the function will eventually decrease, we can go ahead with the Integral Test:
\(\displaystyle \int_{{\,1}}^{{\,\infty }}{{x{{{e}}^{ - {x^2}}}\,dx}} & = \mathop {\lim }\limits_{t \to \infty } \int_{{\,1}}^{{\,t}}{{x{{{e}}^{ - {x^2}}}\,dx}}\hspace{0.5in}u = - {x^2}\\ & = \mathop {\lim }\limits_{t \to \infty } \left. {\left( { - \frac{1}{2}{{{e}}^{ - {x^2}}}} \right)} \right|_1^t\\ & = \mathop {\lim }\limits_{t \to \infty } \left( {-\frac{1}{2}{{e}}^{ - {t^2}}-\biggr(-\frac{1}{2e}\biggr)}} \right) = \frac{1}{2e}\)
Therefore, since the integral is convergent, the series must also be convergent by the Integral Test.
PLEASE ANSWER FAST I HAVE A TEST 100 POINTS
The graph shows the earning from a bake sale per item sold. Which equation represents the earnings from the bake sale?

Answers
Answer:
y = 5x
Step-by-step explanation:
Answer:
B, y= 5x
Step-by-step explanation:
If you look closely to the graph on the "bake sale items" side, when they sold 1 item they earned 5$. And when they sold 5 items they earned 25$. Which would mean every item they sold they get 5$ back which would make it B
what is the last answer and how do I graph player two? i don’t remember how to write an equation in vertex form


Answers
The graph of the player two's function g(t)=16(t-5)²+290 is given in the attachment. The baseball's maximum height is 290 ft. At 5 seconds the baseball was at its maximum height. After 9.25 second the baseball hit the ground.
What is function?A function is a mathematical device that converts one value to another in a predictable manner. We can think of it as a machine. You give the machine an input, it performs some calculations on it, and then returns another value - the result of the calculations.
The function's name is f. We can call it anything we want, but single letters are common. The input* value is referred to as x. Again, we could use anything, but x is common. What the function does with the input is shown to the right of the equals sign.
In this case, the function takes the input x, multiplies it by three, and returns the result.
Learn more about function
https://brainly.com/question/12431044
#SPJ1

Please help me i am struggling only do the left side

Answers
Answer:
1. Y = -1/4x + 1
3. Y = 2/5x + 1
5. Y = 4/5x + 5
7. Y = -x + 5
9. Y = -5/2x - 16
Step-by-step explanation:
Find the slope using the formula
Use the slope and one of the points to find the y-intercept
Once you know the value for m and the value for b, you can plug these into the slope-intercept form of a line (y = mx + b) to get the equation for the line.
A Bernoulli counting process has the following realization No-0, N-1, N2 = 1, N3 = 1, N4 = 2, Ns = 3, No = 3, N7 - 4, No = 4, N, - 5. a) What is the value of X6? b) What is the value of S;? c) What is the value of T2? d) If the success probability is p=0.2, What is P{N2=1, Ns=3, N7-4}?
Answers
Value of X6 = N6 - N5. From the given realization of the Bernoulli counting process, N5 = 3 and N6 - N5 = X6. Hence, X6 = N6 - N5 = 5 - 3 = 2. The value of S is the largest value of n for which Nn = 3. From the given realization of the Bernoulli counting process, N3 = 1, N4 = 2, N5 = 3, and N6 = 5. Hence, the value of S is 5.
The value of T2 is the time at which the second success occurs. From the given realization of the Bernoulli counting process, N2 = 1. Hence, the time at which the second success occurs is T2 = 2.d) P{N2=1, Ns=3, N7-4} = P{N2=1} × P{Ns-N2=2} × P{N7-Ns=1} × P{No=4}.Using the Bernoulli counting process, the probability of a success is p = 0.2 and the probability of a failure is q = 1 - p = 0.8. Therefore, P{N2=1} = pq, P{Ns-N2=2} = p²q, P{N7-Ns=1} = pq², and P{No=4} = p³.Thus, P{N2=1, Ns=3, N7-4} = (0.2)(0.8)(0.2²)(0.8)(0.2)(0.8²)(0.2³) = 0.0016384. A Bernoulli counting process is a stochastic process that consists of a sequence of independent and identically distributed random variables, where each random variable takes the value 1 or 0 with probability p and q = 1 - p, respectively. The Bernoulli counting process is often used to model the arrival times of events that occur randomly over time. The Bernoulli counting process has many applications in areas such as reliability theory, queueing theory, and inventory management.In this question, we are given the realization of a Bernoulli counting process, and we are asked to find various quantities associated with this process. We are first asked to find the value of X6, which is the number of successes that occur between times 5 and 6. We are then asked to find the value of S, which is the largest time at which three successes have occurred. We are also asked to find the value of T2, which is the time at which the second success occurs. Finally, we are asked to find the probability of a specific sequence of events occurring, given that the success probability is p = 0.2.To find the value of X6, we simply subtract the value of N5 from the value of N6. Similarly, to find the value of S, we look for the largest time at which Nn = 3. To find the value of T2, we look for the time at which N2 = 1. Finally, to find the probability of a specific sequence of events occurring, we use the probabilities of success and failure to calculate the probability of each event occurring, and then multiply these probabilities together. Thus, we have found the value of X6, the value of S, the value of T2, and the probability of a specific sequence of events occurring.
In conclusion, the Bernoulli counting process is a powerful tool for modeling the arrival times of events that occur randomly over time. By using the probabilities of success and failure, we can calculate various quantities associated with this process, such as the value of X6, the value of S, the value of T2, and the probability of a specific sequence of events occurring. The Bernoulli counting process has many applications in areas such as reliability theory, queueing theory, and inventory management.
To learn more about Bernoulli counting process visit:
brainly.com/question/24232842
#SPJ11
write the set b=1/10 1/100 1/1000 in set builder form
Answers
The set builder form of the set b = {1/10, 1/00, 1/1000} is b = {x | x = 1/10ⁿ, where n is a positive integer}
In mathematics, set builder notation is a concise way of describing a set using a rule or a formula.
Let's explore how we can use set builder notation to write the set b={1/10, 1/100, 1/1000}.
To begin, we need to identify the common property that these elements share. In this case, we can observe that each element is a rational number with a power of ten as the denominator. So, we can write the set b as follows:
b = {x | x = 1/10ⁿ, where n is a positive integer}
In this notation, the vertical bar represents "such that" and separates the description of the element from the rule that defines the set. The letter x is a variable that represents any element that satisfies the rule. We use the power of ten as a common property to describe the set b.
In this set builder form, we can see that b is a set of elements that can be expressed as 1/10 to the power of a positive integer. We can also use set builder notation to define other sets with different properties, such as sets of even numbers or sets of prime numbers.
To know more about set here.
https://brainly.com/question/28276299
#SPJ4
A rectangle has a length of 8.2 feet and a width of 3.5 feet. What is the area?
A
23.4 ft
B
11.7 ft
C
28.7 ft
D
4.7 ft
Answers
Answer:
C 28.7
Step-by-step explanation:
Remember this formula if you want to find the Area of rectangle = A = L X W
How do you answer this?!?!?!?!??!
Step A: Determine the volume of the following figure. Round to the nearest tenth.
Step B: Determine the surface area of the figure. Round to the nearest tenth.
Step C: In a short paragraph, explain in your own words your work for Steps A and B.

Answers
Answer:
use a calculator to find 3x3x7 for step one and for step 2 times 3x3 in a calculator
Step-by-step explanation:
(3+5)2-(2-4)÷2+5(3-4)
Answers
Answer: this is the answer
Step-by-step explanation:

Length = 9.8 cm
Width = 5.5 cm
Height = 4.3 cm
Volume?
Answers
Answer:
231.77
we have length as9.8cm
breadth as 5.5cm
height as 4.3cm
solution
we know that
volume =l*b*h
=9.8*5.5*4.3
=231.77
HELP PLEASE. I DONT KNOW IF ITS 30 OR 180

Answers
To see why, we can simplify √180 as follows:
√180 = √(36 × 5) (since 36 is a perfect square that can be factored out)
√180 = √36 × √5 (using the product rule of square roots)
√180 = 6√5
Therefore, 6√5 is equivalent to √180.
Answer:
Step-by-step explanation:
6\(\sqrt{5\\\)
\(\sqrt{5*36}\)
\(\sqrt{180}\)
If you think about it logically, how can you take 6 out? So there was a number 36 under the root, and because of that there is a possibility to take it out, because 6 squared is 36
Nathan Reynolds bought a car for $15,000. He made a down payment of $3,000. Nathan secured a loan for the balance of the purchase price at 8 percent interest for four years.
determine the monthly payment and total interest
Answers
Answer:
1) The monthly payment is approximately $292.96
2) The total interest is approximately $2,061.84
Step-by-step explanation:
1) The financing method Nathan Reynolds applied to buy the car is given as follows;
The purchase price of the car = $15,000
The down payment made for the car = $3,000
The
The interest on the loan he took for the balance of the purchase price, R = 8%
The number of years for which he took the loan, n = 4 years = 48 months
We have;
The balance of the purchase price = (The purchase price of the car) - (The down payment made for the car)
∴ The balance of the purchase price = $15,000 - $3,000 = $12,000
The balance of the purchase price = $12,000 = The loan Nathan secured
The monthly payment on a loan is given by the following formula
\(A = P \times \dfrac{r \cdot (1 + r)^n}{(1 + r)^n - 1}\)
Where;
A = The payment amount made monthly
P = The principal or loan amount = $12,000
r = The interest rate divided by 12 = R/12 = 8/12 = 2/3
n = The number of months the monthly payment will be made = 48 months
By plugging in the variable values, we get;
\(A = 12,000 \times \dfrac{\dfrac{2}{300} \times \left (1 + \dfrac{2}{300} \right ) ^{48}}{ \left (1 + \dfrac{2}{300} \right )^{48} - 1} = 292.955068099 \approx 292.96\)
Therefore, the payment amount made monthly, A ≈ $292.96
2) The total payment made in the 48 months = A × 48 = 292.955068099 × 48 ≈ 14,061.84
The total payment made in the 48 months ≈ $14,061.84
The total interest = (The total payment made in the 48 months) - (The loan amount)
∴ The total interest = $14,061.84 - $12,000 ≈ $2,061.84
APEX PRE CALC: For a ____ function, the domain is broken into pieces, with a different rule defining the function for each piece.

Answers
Answer:
Piecewise
Step-by-step explanation:
For a piecewise function, the domain is broken into pieces, with a different rule defining the function for each piece.
Piecewise functions are usually a function that equals two or more equations depending on the x or the domain.
Google piecewise functions to see examples.
I hope this helps!
Answer: Piecewise
Step-by-step explanation:
There will be breaks and jumps in the curve, particularly when a value would undefined. So the solution curve looks like disconnected pieces.
PLEASE HELP ME I AM GROUNDED AND NEED THIS FINISHED NOWWW
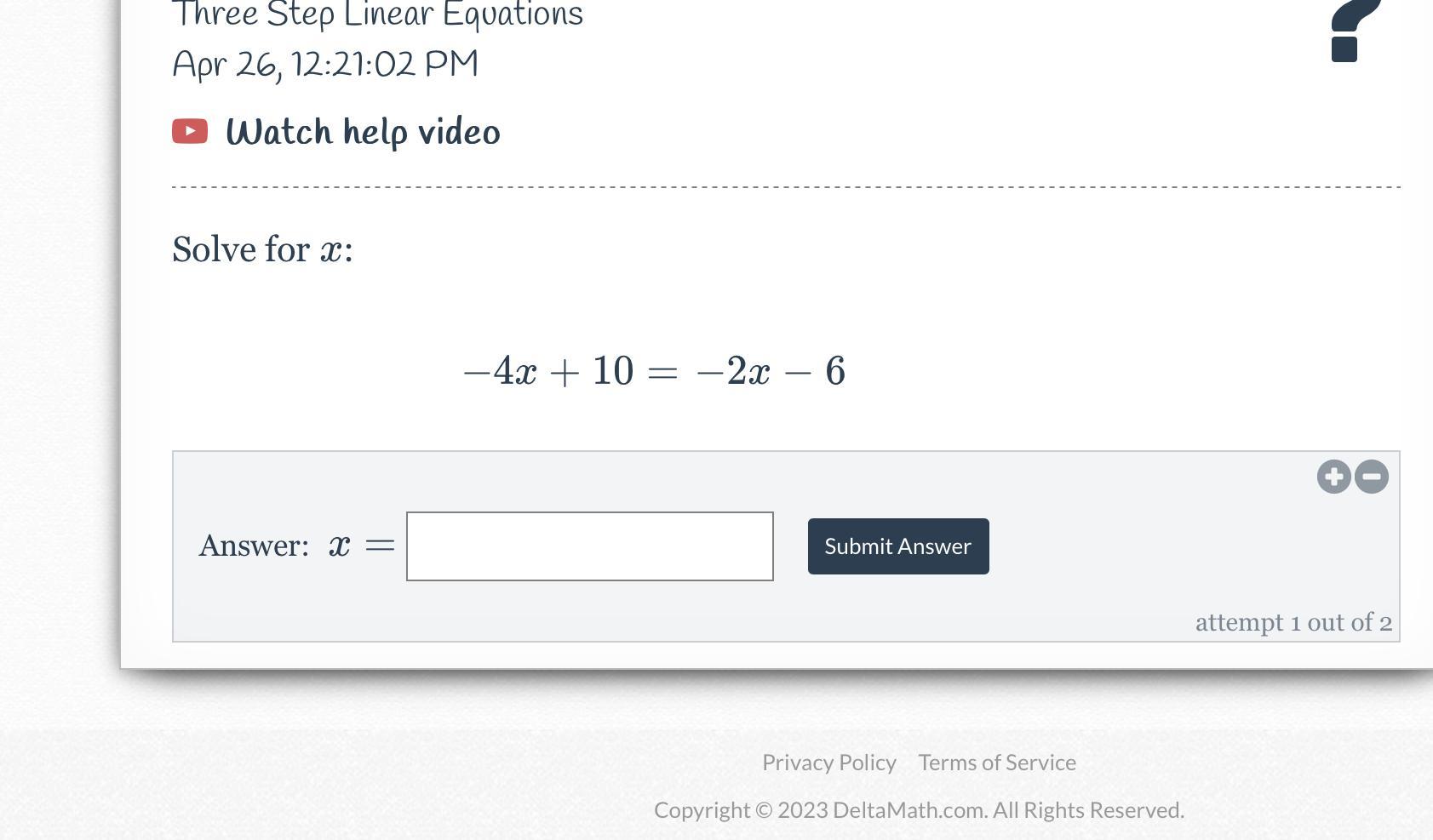
Answers
Answer:
x = 8
Step-by-step explanation:
-4x + 10 = -2x - 6
-4x + 2x = -6 - 10 (Calculate)
-2x = -16 (Divide both sides by -2)
x = 8
Have a nice day! :D
Answer:
x=8
Step-by-step explanation:
-4x+10=-2x-6 original equation
-4x+16=-2x add 6 both sides
16=2x add 4 both sides
x=8 divide 2 both sides
Given the points (-2, 0), (-1,0), (0, – 8), (2, 0), write the polynomial in factored form.
Answers
As per given by the question,
There are given that four point.
The point is,
\((-2,\text{ 0), (-1, 0), (0, -8), (2, 0)}\)Now,
From given point,
\((-2,\text{ 0), (-1, 0), (0, -8), (2, 0)}\)Then, the factor is,
\((x+2)(x+1)(x-2)\)Now, solve the above equation,
\((x+2)(x+1)(x-2)\)The factorial formd will be,
\(y=a\times(x+2)\times(x+1)\times(x-2)\)Now, find the value of "a" with the help of given point (0, -8).
So,
Puth the value of x =0, and y=-8 in above equation,
Then,
\(\begin{gathered} y=a\times(x+2)\times(x+1)\times(x-2) \\ -8=a\times(0+2)\times(0+1)\times(0-2) \\ -8=a(2)(1)(-2) \\ a=\frac{-8}{-4} \end{gathered}\)Then, a=2.
Now,
The value of a is 2.
And,
The polynomial in the factored form is,
\(y=2(x+2)(x+1)(x-2)\)Hence, the value of a is 2 and the polynomial in the factored form is,
\(y=2(x+2)(x+1)(x-2)_{}\)Nico earns $12.50 per hour as a math tutor. Show that the relationship between the amount he earns and the number of hours he tutors is a proportional relationship. What is the constant of proportionality (k). Then write the equation for the relationship.
Answers
Answer:
12.50k
Step-by-step explanation:
I came to this answer as k is the number of hours, and 12.50 is how much per hour.
Approximate the square root to the nearest integer.
37

Answers
Answer:
We know that 6² = 36 , which is very close to 37 . Thus square root of 37 will be very close to 6
How to solve this first order linear differential equation?
Answers
To find first-order linear differential equations solution, we have to derive the general form or representation of the solution.
With the help of the steps shown below, we can learn how to solve the first-order differential equation.
1. Reorder the terms in the given equation so that they have the form \($\frac{dy}{dx}+Py=Q\) where P and Q are constants or functions of the independent variable x only.
2. Integrate P (obtained in step 1) with respect to x and then put this integral as a power of e to determine the integrating factor.
\($e^{\int P d x}\) = IF
3. The linear first-order differential equation's two sides should be multiplied by the IF.
4. The L.H.S of the equation is always a derivative of \($y \times M(x)$\) i.e. L.H.S \($= \frac{d(y \times I . F)}{dx}\)
\($d(y \times I . F) d x=Q \times I . F$\)
5. In order to arrive at the solution, we simply integrate both sides with respect to x in the last step.
Therefore \(y \times I . F=\int Q \times I . F d x+C$,\)
where C is some arbitrary constant
Similarly, we can also solve the other form of linear first-order differential equation \($\frac{dy}{dx}+Py=Q\) using the same steps.
P and Q are y's functions in this manner. We determine the solution, which will be, by using the integrating factor (I.F), which is
\($(x) \times(I . F)=\int Q \times I . F d y+c$\)
Now, to get a better insight into the linear differential equation, let us try solving some questions. where C is some arbitrary constant.
For more questions on differential equation
https://brainly.com/question/12423682
#SPJ4
Find the slope of the line that passes through the given points.
(−3, 5), (0, −1)
.
.
please help
Answers
Answer:
m = − 2
Step-by-step explanation:
Answer:
0 Is the answer 0 - 1 / 0 - 3 = 0
simplify 2x
2
−2x−24
x
2
−5x−24
⋅
x
2
−10x+16
x
2
−4
÷
2x
2
−5x−12
12x+24
Answers
The expressions when simplified are
(a) 3x² - 7x - 48
(b) 2x² - 10x + 12
(c) 2x² + 7x + 12
How to simplify the expressionsFrom the question, we have the following parameters that can be used in our computation:
The expressions
To simplify the expressions, we collect the like terms and evaluate them
Using the above as a guide, we have the following equations
2x² −2x −24 + x² −5x −24 = 3x² - 7x - 48
x² − 10x + 16 + x² − 4 = 2x² - 10x + 12
2x² − 5x − 12 + 12x + 24 = 2x² + 7x + 12
Read more about expression at
https://brainly.com/question/32302948
#SPJ4
Question
Simplify
2x² −2x −24 + x² −5x −24
x² − 10x + 16 + x² − 4
2x² − 5x − 12 + 12x + 24
pls help me ASAP
ty

Answers
Step-by-step explanation:
D = b² - 4ac
#1D = 10² - 4 · 3 · 2
D = 100 - 24
D = 76
#2D = (-5)² - 4 · 1 · (-4)
D = 25 - (-16)
D = 26 + 16
D = 42
#3D = 7² - 4 · 1 · (-8)
D = 49 - (-32)
D = 49 + 32
D = 81
#4D = 0² - 4 · 1 · (-9)
D = 0 - (-36)
D = 36
#5D = (-6)² - 4 · 5 · 10
D = 36 - 200
D = - 164