Answers
Answer:
15 square meters
Step-by-step explanation:
when it says find the area you have to add all the lengths together
Related Questions
Select the mean, median, mode and range of the following list of values.1, 2, 4,7Averages3.5None36MeanMedianRangeMode
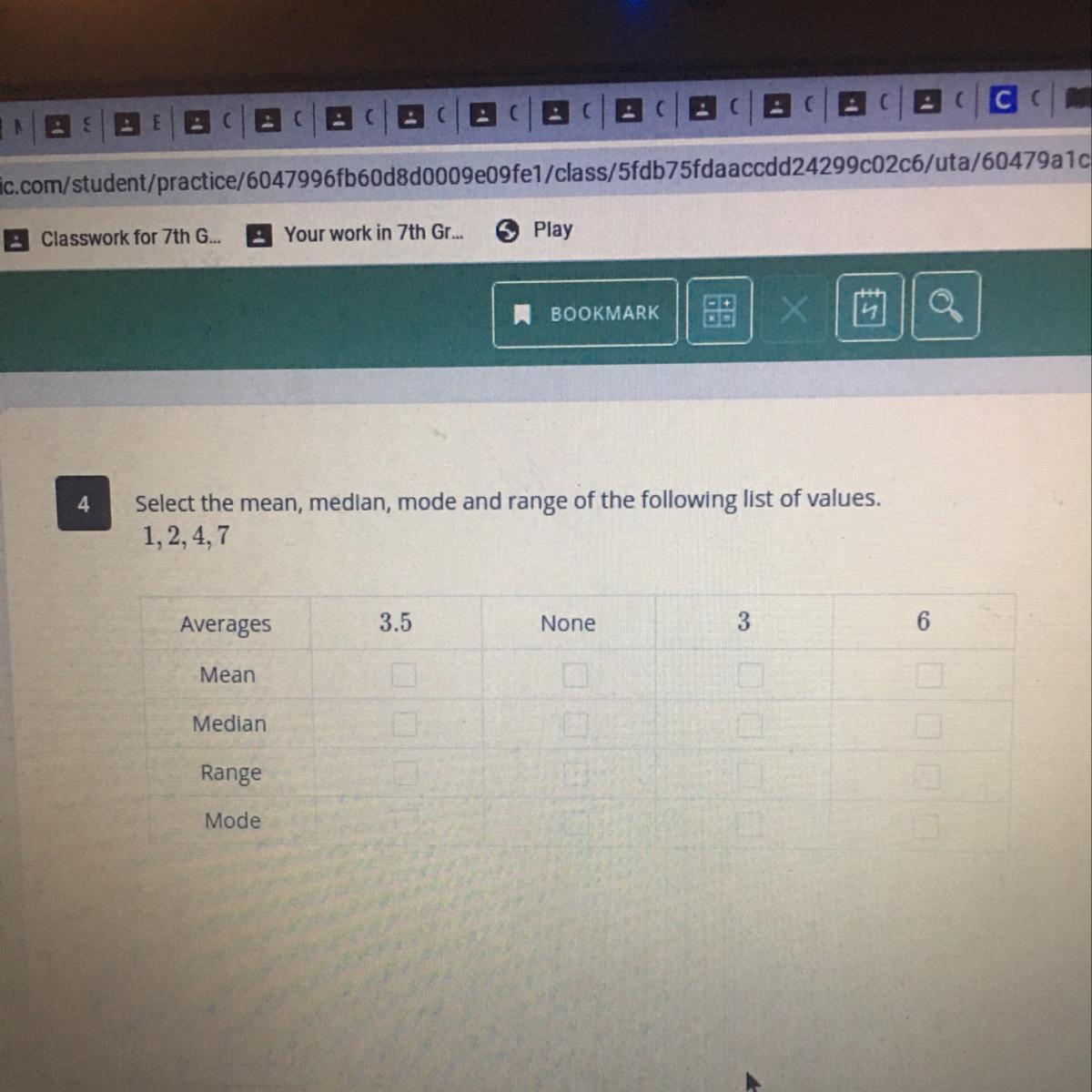
Answers
The data set is
1, 2, 4, 7
The answers are;
\(\begin{gathered} \text{Mean}=\frac{1+2+4+7}{4} \\ \text{Mean}=\frac{14}{4} \\ \text{Mean}=3.5 \end{gathered}\)\(\begin{gathered} \text{Median}=\frac{2+4}{2} \\ \text{Median}=\frac{6}{2} \\ \text{Median}=3 \end{gathered}\)The median in a case where the data set is an even number, then the median would take account of both middle values and then calculate addition of both and then divide by 2
The Mode is the most frequently occuring value in the data set. In this case, all observed data occur just once, and none of them occur more than once. Hence there is no Mode
\(\begin{gathered} \text{Range}=\text{Highest value-Lowest value} \\ Range=7-1 \\ \text{Range}=6 \end{gathered}\)Pete traveled 1,380 miles in two days. The first day, he traveled 1.5 times as far as he did the second day. How many miles did he drive on
Answers
He drove 828 miles on the first day.
An algebraic expression is the combination of numbers and variables in expressing and solving a particular mathematical question.
Let x = distance Pete traveled on the second day
If on the first day, he traveled 1.5 times as far as he did the second day, then
distance Pete traveled on the first day = 1.5x
If Pete traveled 1,380 miles in two days, the the sum of the distance he traveled in two days is equal to 1380.
x + 1.5x = 1380
Simplify the equation and solve for the value of x.
x + 1.5x = 1380
2.5x = 1380
x = 552
distance Pete traveled on the second day = 552 miles
distance Pete traveled on the first day = 1.5(552) = 828miles
Therefore, he drove 828 miles on the first day.
The problem seems incomplete. The question must be
"Pete traveled 1,380 miles in two days. The first day, he traveled 1.5 times as far as he did the second day. How many miles did he drive on the first day?"
Learn more about algebraic expression here: brainly.com/question/4344214
#SPJ4
ari thinks the perfect milkshake has 5 scoops of ice cream for every 3 spoonfuls of caramel. freeze zone makes batches of milkshakes with 10 scoops of ice cream and 7 spoonfuls of caramel. what will ari think about the amount of caramel in freeze zone's milkshakes?
Answers
Answer:
Step-by-step explanation:
Since we have been given that
Ari has 3 ounces of caramel for each 5 scoops of frozen yogurt .
Freeze Zone makes bunches of milkshakes with 6 ounces of caramel and 8 scoops of frozen yogurt.
As per Ari,
For each 5 scoops of frozen yogurt, he wants 3 ounces of caramel
For each 1 scoop of frozen yogurt, he wants
3 ounces of Caramel
For each 8 scoops of frozen yogurt, he wants
3/5 * 8 = 24/5= 4.8 ounces
In this way, Ari considers sum caramel is something else for ideal milkshake as there is just requirement for 4.8 ounces of caramel however Freeze Zone is utilizing 6 ounces of caramel.
Answer:
Step-by-step explanation:
5456
What is the solution to the system equation?
y=-5x+3
y=1
Answers
Answer:x= 2/5
Step-by-step explanation:
Can Someone answer this pleaseee
Matthew has a jar of 368 nickels and dimes he has been collecting. The total value of the coins is $28.40.Which system of linear equations and solution can be used to represent the number of nickels and dimes Matthew has in his collection?
A. n + d = 368 0.05n + 0.1d=28.4 168 nickels and 200 dimes
B. n + d = 368 0.01n + 0.05d=28.4 200 nickels and 168 dimes
C. n + d = 368 0.05n + 0.1d=28.4 200 nickels and 168 dimes
D. n + d = 368 0.1n + 0.05d=28.4 168 nickels and 200 dimes
Answers
Answer:
\(n + d = 368\)
\(0.05n + 0.10d = 28.40\)
Step-by-step explanation:
Given
\(Total = 368\)
\(Value = \$28.40\)
Required
Determine the linear equations to represent the scenario
Represent nickel with n and dimes with d
So, the total is:
\(n + d = 368\)
\(1\ nickel = \$0.05\)
\(1\ dime = \$0.10\)
So, the value is:
\(0.05n + 0.10d = 28.40\)
Hence, the linear equations are:
\(n + d = 368\)
\(0.05n + 0.10d = 28.40\)
The system of linear equations and solution can be used to represent the number of nickels and dimes Matthew has in his collection is n + d = 368 0.05n + 0.1d=28.4 168 nickels and 200 dimes.
Given that,
Matthew has a jar of 368 nickels and dimes he has been collecting. The total value of the coins is $28.40.Here we take n be nickles and d be dimes. Also, 1 nickel be = $0.05 and 1 dime be $0.10.Based on the above information, the calculation is as follows:
n + d = 368
So,
d = 368 - n
And,
0.05n + 0.10d = 28.40
0.05n + 0.10(368 - n) = 28.40
0.05n + 36.8 - 0.10n = 28.40
0.05n = 8.4
n = 168
So, d = 368 - 168
= 200
Therefore we can conclude that the correct option is A.
Learn more: brainly.com/question/16115373
Students are getting signatures for a petition to increase sports activities at the community center. The number of signatures they get each day is twice as many as the day before. The expressin 2 to the power of 6 represents the number of signatures thry got on thr sixth dsy. How many signatures did they grt on the first day?
Answers
The number of signatures they got on the first day is 2.
The problem can be solved mathematically by using the formula for geometric sequences, which is:
an = a1 × r^(n-1)
where:
an = the nth term in the sequence
a1 = the first term in the sequence
r = the common ratio between consecutive terms
n = the number of terms in the sequence
In this case, we know that the number of signatures they get each day is twice as many as the day before, which means that the common ratio is 2. We also know that the number of signatures they got on the sixth day is 2^6 = 64.
Using the formula for geometric sequences, we can solve for a1 by substituting the known values
64 = a1 × 2^(6-1)
64 = a1 × 2^5
a1 = 64 / 2^5
a1 = 2
Learn more about geometric sequence here
brainly.com/question/13008517
#SPJ4
Question 16 of 35
Henri earned $1030 a week last year. What was his yearly salary?
OA. $54,600
OB. $53,560
OC. $52,800
OD. $49,440
SUBMIT
Answers
Explanation: there are 52 weeks in a year, so 1030 x 52 = 53,560
Find the amount accumulated after
investing a principal P for t years at an
interest rate compounded annually.
P = $15,500
r = 9.5%
t = 12
Hint: A = P (1 + ) kt
A = $[?]
Round your answer to the nearest cent (hundredth).

Answers
The amount accumulated after investing a principal P for t years at an interest rate compounded annually is $46,057.58.
How to solve compound interest ?Compound interest is the interest you earn on interest. Compound interest is the interest calculated on the principal and the interest accumulated over the previous period.
Therefore, let's find the amount accumulated after investing a principal P for t years at an interest rate compounded annually.
\(A = p(1 + \frac{r}{n} )^{nt}\)
where
P = principalr = ratet = timen = number of timep = 15,500
r = 9.5%
t = 12
n = 1
\(A = 15500(1 + \frac{0.095}{1} )^{1(12)}\)
A = 15,500.00(1 + 0.095)¹²
A = $46,057.58
learn more on compound interest here: https://brainly.com/question/13803287
#SPJ1
$46,057.58, answer for acellus
I’m working on circumferences,area,diameter and radius of circles and I need help to find/calculate and how to use the methods
Answers
Answer:
Circumference of a circle is 2 pie r
Area of a circle is pie r^2
Diameter is 2radius, that is radii makes up a diameter
Radius of a circle is half of the diameter
Please mark as brainliest
Express the confidence interval 0.039
A. 0.259+0.22B. 0.22±0.5
C. 0.259+0.5
D. 0.259+0.44
Answers
The confidence interval is 0.039. This means that the value lies between the range of -0.039 and 0.039. Therefore, we can express the confidence interval as the mean plus or minus the margin of error.
This will give us a range in which the true population mean lies.Let's assume that the mean is 0.259. Then the lower limit of the range is given by:Lower limit = 0.259 - 0.039 = 0.22 And the upper limit of the range is given by:Upper limit = 0.259 + 0.039 = 0.298Therefore, the confidence interval is: 0.22 to 0.298Now we can see that option A is the correct answer: 0.259+0.22.
Learn more about confidence interval
https://brainly.com/question/32546207
#SPJ11
when a researcher rejects the null hypothesis, the difference is declared to be: select one: a. statistically significant. b. statistically insignificant. c. statistically unimportant. d. statistically strong.
Answers
Answer:
C
Step-by-step explanation:
what is the percent of games won if a team won 92 games and lost 58 games?
Answers
Answer:
I think this is it 61.33
Have a blessed day <333
Step-by-step explanation:
There is a function f(t) which is given by:
f(t) = sin(t/T) for 0 ≤ t ≤ 2πT and
f(t) = 0 for 2πT ≤ t
This function repeats periodically outside the interval [0,T] with period T (assuming that 2πT
a) what are the restrictions that would be expected for the Fourier coefficient a_j. Which Fourier coefficient is expected to be the largest?
b) Calculate the Fourier expansion , thus verifying the prediction .
Answers
a) The largest Fourier coefficient is a_1.
b) The final answer is:f(t) = (2/π) [sin(t/T) - (1/3) sin(3t/T) + (1/5) sin(5t/T) - ...]
a) Restrictions for Fourier coefficient a_j
The Fourier coefficients for odd functions are odd and for even functions, the Fourier coefficients are even. This function is odd, so a_0 is equal to zero. This is due to the function being odd about the origin. Hence, only odd coefficients exist.
For the given function f(t), f(t) is continuous, and hence a_0 is equal to 0. So, the restrictions on the Fourier coefficient a_j are:
For j even, a(j) = 0, For j odd, a(j) = (2/T)
= ∫[0,T] sin(t/T) sin(jπt/T) dt = (2/T)
= ∫[0,T] sin(t/T) sin(jt) dt.
The largest Fourier coefficient is the one with the highest value of j. Hence, for this function, the largest Fourier coefficient is a_1.
b) Calculating the Fourier expansion using the Fourier series
We know that the Fourier coefficients for odd functions are odd, and for even functions, the Fourier coefficients are even. This function is odd, so a_0 is equal to zero. Thus, the Fourier expansion of the given function is:
f(t) = Σ[1,∞] a_j sin(jt/T), where a_j = (2/T)
= ∫[0, T] sin(t/T) sin(jt) dt
= (2/T) ∫[0, T] sin(t/T) sin(jπt/T) dt,
since j is odd.
Now, let us evaluate the integral using integration by parts by assuming u = sin(t/T) and v' = sin(jπt/T).
Then we get the following: du = (1/T) cos(t/T) dt
dv' = (jπ/T) cos(jπt/T) dt
Integrating by parts, we have: a(j) = [2/T]
(uv)|_[0,T] - [2/T]
∫[0,T] u' v dt = [(2/T) (cos(Tjπ) - 1) sin(T/T) + jπ(2/T) ∫[0,T] cos(t/T) cos(jπt/T) dt]/jπ
Using the trigonometric identity, cos(A) cos(B) = 0.5 (cos(A-B) + cos(A+B)), we have:
a(j) = [(2/T) (cos(Tjπ) - 1) sin(T/T) + jπ(2/T) ∫[0, T] cos((jπ-Tπ)t/T)/2 + cos((jπ+Tπ)t/T)/2 dt]/jπ
= [(2/T) (cos(Tjπ) - 1) sin(T/T) + (2/T) sin(jπ)/2 + (2/T) sin(jπ)/2]/jπ,
since the integral is zero (because cos((jπ-Tπ)t/T) and cos((jπ+Tπ)t/T) are periodic with period 2T).
Thus, we get the following expression for a(j): a(j) = [(2/T) (cos(Tjπ) - 1) sin(T/T)]/jπ.
So, the Fourier series expansion of the given function is f(t) = Σ[1,∞] [(2/T) (cos(Tjπ) - 1) sin(T/T)] sin(jt/T) / jπ.
Hence, the final answer is:f(t) = (2/π) [sin(t/T) - (1/3) sin(3t/T) + (1/5) sin(5t/T) - ...]
To know more about Fourier expansion,
https://brainly.com/question/24108818
#SPJ11
write the first six cube if natural number
Answers
Answer:
1³ = 1
2³ = 8
3³ = 27
4³ = 64
5³ = 125
6³ = 216
Step-by-step explanation:
Answer:
The cube of first six natural numbers are
1, 8, 27, 65, 125, 216
Step-by-step explanation:
Natural Numbers are known as 1, 2, 3, 4, ..., ∞
Now,
For Cube of first six natural numbers
1³ = 1
2³ = 8
3³ = 27
4³ = 64
5³ = 125
6³ = 216
Thus, The cube of first six natural numbers are
1, 8, 27, 65, 125, 216
-TheUnknownScientist
Alisha is an author who receives a 15% royalty payment for every book sold my her publisher. Her book sells for $21.95 and the publisher sold 100,000 copies this year. How much did Alisha get paid ? (I’m just checking my answer) I got 329,250
Answers
3.2925 x 100,000 = 329 250
Therefore your answer is correct
Meghan sells handmade sweaters and hats at her store. Let A represent the event that a randomly selected customer buys hat, and let B
represent the event that a randomly selected customer buys a sweater.
What does the notation P(AJB) represent in terms of the context?
A the probability that a customer buys a hat or a sweater
B the probability that a customer buys both a hat and a sweater
C the probability that a customer buys a hat given that the customer has bought a sweater
D the probability that a customer buys a sweater given that the customer has bought hat
Answers
Answer:
Step-by-step explanation:
C the probability that a customer buys a hat given that the customer has bought a sweater.
Please come and help me with this! Best Answer get Brainliest!!!!! :D
Please number your responses to the questions as they are shown (1a, 1b)
a. Create a quadratic expression in standard form.
b. Rewrite the expression by completing the square. Explain your work using complete sentences.
Answers
Answer:
A = Solve 5x2 + 6x + 1 = 0
B= Coefficients are: a = 5, b = 6, c = 1
Quadratic Formula: x = −b ± √(b2 − 4ac)2a
Put in a, b and c: x = −6 ± √(62 − 4×5×1)2×5
Solve: x = −6 ± √(36 − 20)10
x = −6 ± √(16)10
x = −6 ± 410
x = −0.2 or −1
Answer: x = −0.2 or x = −1
Step-by-step explanation:
there you go
mrs. hansen asked eli to apply the distributive property to the expression, 2(7 3). which of the following should eli have not written?
A. 2(10)
B. 2(7) =2(3)
C. 2(3+7)
D. (7+3).2
Answers
Eli should not have written option D, (7+3).2, when applying the distributive property to the expression 2(7+3).
The distributive property states that when you multiply a number by a sum or difference inside parentheses, you need to multiply the number by each term inside the parentheses. In this case, Eli needs to multiply the number 2 by each term inside the parentheses (7 and 3). Let's analyze each option:
A. 2(10): Eli correctly applied the distributive property by multiplying 2 by 10, which is the result of adding 7 and 3.
B. 2(7) = 2(3): Eli correctly applied the distributive property by multiplying 2 by both 7 and 3 separately.
C. 2(3+7): Eli correctly applied the distributive property by multiplying 2 by the sum of 3 and 7.
D. (7+3).2: This expression does not apply the distributive property correctly. The parentheses indicate addition, not multiplication. Eli should have multiplied 2 by both 7 and 3, rather than adding them first.
Therefore, option D is the incorrect one, and Eli should not have written (7+3).2 when applying the distributive property to the given expression.
Learn more about distributive property here:
https://brainly.com/question/30321732
#SPJ11
What is the best description of the relation in Item 2?
O A
a function that is one-to-one
0
В.
a function that is many-to-one
o
C.
a function that is one-to-many
O
D.
a relation that is not a function
Help me please
Answers
please please please helpppp

Answers
Problem 2 A local girls soccer team decides to sell chocolate bars to raise some money for new uniforms. The girls are to receive 10% of all the sales they make. Once the bars arrive the girls see that they have to sell each bar for $2.50. They think this price is too high. Are the girls being altruistic or is there something else going on? (Assume the girls face a downward sloping demand curve).
Answers
The girls' reluctance to sell the chocolate bars at $2.50 per bar may not be purely altruistic but instead driven by their understanding of market demand and the potential impact of pricing on sales volume.
The girls' perception that the selling price of $2.50 per chocolate bar is too high may not necessarily indicate altruism but rather a response to market demand. When faced with a downward sloping demand curve, higher prices can lead to lower sales volume.
The girls' concern may be rooted in their understanding that a higher price could potentially deter potential buyers from purchasing the chocolate bars, resulting in lower overall sales and potentially lower earnings for themselves.
By considering the demand curve, the girls are likely taking into account the price elasticity of demand. Elastic demand implies that a change in price will have a relatively larger impact on the quantity demanded. If the girls perceive the demand for chocolate bars to be elastic, they might believe that a lower price would attract more customers and lead to increased sales volume.
Their concerns could also be motivated by their desire to achieve a balance between maximizing their sales and ensuring a reasonable profit margin. They might be aware that setting the price too high could lead to reduced demand and lower overall revenue, thereby limiting their earnings.
Learn more about volume here:
https://brainly.com/question/28058531
#SPJ11
A robot vacuum advertises that it can clean a 120-square-foot room in 1/2 an hour. How many square feet could the robot vacuum clean in 1 hour?
Answers
Answer: 240 square foot room
Step-by-step explanation: They ask for how many square feet in 1 hour which is double the 1/2 hour. So, just do 120x2=240 to get your answer! (Don’t forget to label ,square-feet,)
A can lid has a radius of 3 in.
What is the area of the can lid?
9π in2
3π in2
9 in2
3 in2
Answers
Answer:
9 * pi inches squared
Step-by-step explanation:
1 and 2 is all I need and you guys would help me from not getting beat

Answers
Answer:
1. -10
2. -11
Step-by-step explanation:
Let U = {a, b, c, d, e, f}, A = {d, e, f}, B = {c, e, f, and C = {b, c, d}. Find the following set. AU(BNC)
Answers
:A U (B ∩ C) is the set containing all elements that are in A or in both B and C (which is the intersection of B and C).
The given sets U = {a, b, c, d, e, f}, A = {d, e, f}, B = {c, e, f}, and C = {b, c, d}.We need to find AU(BNC).We first calculate B ∩ C, which is the intersection of B and C. We see thatB ∩ C = {c}Then, we need to take the union of A and B ∩ C. We see thatA U (B ∩ C) = {d, e, f, c}.Thus, the set AU(BNC) is equal to {d, e, f, c}.
Summary:We need to find AU(BNC).We first calculate B ∩ C, which is the intersection of B and C. We see that B ∩ C = {c}.Then, we need to take the union of A and B ∩ C. We see that A U (B ∩ C) = {d, e, f, c}.Thus, the set AU(BNC) is equal to {d, e, f, c}.
Learn more about sets click here:
https://brainly.com/question/13458417
#SPJ11
Activity 2: Identify Me
Direction: Determine whether each pair of triangles is congruent by SSS, SAS, ASAor AAS. If it is not possible to prove that they are congruent, wnte NOT POSSIBLE

Answers
Step-by-step explanation:
SSS axiomSAS axiomASA axiomASA axiomSAS axiomSSS axiomF (x) is a function

Answers
Answer:
True
Step-by-step explanation:
only one output for each input passes the vertical line test
Answer:
A
Step-by-step explanation:
For f(x) to be a function each value of x in the domain must map to exactly one unique value of y in the range.
This is the case here thus f(x) is a function
help asap i forgot to study

Answers
Answer: 2+n
Step-by-step explanation:
Tn=T1 + (n-1) d
3+(n-1)1
3+n-1
3-1+n
2+n
Given the definite integral (20-¹ -1 a. Use Trapezoid Rule with 4 equal subintervals to approximate the value ofthe map o b. Determine whether your answer in part a is an overestimate or an underestimate of he Type your final answer in the solution box below. For full or partial credit on this problem, be sure to show full detailed steps of your work suporty
Answers
Therefore, the approximate value of the definite integral using the Trapezoid Rule with 4 equal subintervals is 52.484375. In this case, the function 20 - x⁴ is concave down within the interval [-1, 2]. Therefore, the approximation using the Trapezoid Rule is likely to be an underestimate.
a. To approximate the definite integral using the Trapezoid Rule with 4 equal subintervals, we divide the interval [-1, 2] into 4 subintervals of equal width.
The width of each subinterval, Δx, is given by:
Δx = (b - a) / n
where b is the upper limit of integration, a is the lower limit of integration, and n is the number of subintervals.
In this case, a = -1, b = 2, and n = 4. Therefore:
Δx = (2 - (-1)) / 4 = 3 / 4 = 0.75
Next, we approximate the integral using the Trapezoid Rule formula:
(20 - x⁴) dx ≈ Δx / 2 × [f(a) + 2f(x₁) + 2f(x₂) + 2f(x₃) + f(b)]
where f(x) represents the function being integrated.
Substituting the values:
integration of [-1, 2] (20 - x⁴) dx ≈ 0.75 / 2 × [f(-1) + 2f(-0.25) + 2f(0.5) + 2f(1.25) + f(2)]
We evaluate the function at the given points:
f(-1) = 20 - (-1)⁴ = 20 - 1 = 19
f(-0.25) = 20 - (-0.25)⁴ = 20 - 0.00390625 = 19.99609375
f(0.5) = 20 - (0.5)⁴ = 20 - 0.0625 = 19.9375
f(1.25) = 20 - (1.25)⁴= 20 - 1.953125 = 18.046875
f(2) = 20 - (2)⁴ = 20 - 16 = 4
Now, we substitute these values into the formula:
integration of [-1, 2] (20 - x⁴) dx ≈ 0.75 / 2 × [19 + 2(19.99609375) + 2(19.9375) + 2(18.046875) + 4]
Calculating the expression:
integration of [-1, 2] (20 - x⁴) dx ≈ 0.75 / 2 × [19 + 2(19.99609375) + 2(19.9375) + 2(18.046875) + 4]
≈ 0.375 × [19 + 39.9921875 + 39.875 + 36.09375 + 4]
≈ 0.375 × [139.9609375]
≈ 52.484375
Therefore, the approximate value of the definite integral using the Trapezoid Rule with 4 equal subintervals is 52.484375.
b. To determine whether the approximation in part a is an overestimate or an underestimate, we need to compare it with the exact value of the integral.
However, we can observe that the Trapezoid Rule tends to overestimate the value of integrals when the function is concave up and underestimates when the function is concave down.
In this case, the function 20 - x⁴ is concave down within the interval [-1, 2]. Therefore, the approximation using the Trapezoid Rule is likely to be an underestimate.
To know more about Trapezoid Rule:
https://brainly.com/question/30425931
#SPJ4
How to prove Rank(AB)â¤min(Rank(A),Rank(B))Rank(AB)â¤min(Rank(A),Rank(B))?
Answers
To prove this \(Rank(AB)â¤min(Rank(A),Rank(B))Rank(AB)â¤min(Rank(A),Rank(B))\) , we use matrices.
If A and B are matrices, then to prove that Rank(AB) ≤ min(Rank(A), Rank(B)), the rank of the matrix is the maximum number of linearly independent rows or columns.
You can use the fact that there is Inside is a matrix.
Suppose A is an m-by-n matrix and B is an n-by-p matrix. In this case, product AB is an m-by-p matrix.
Let rA be the rank of A and rB be the rank of B.
First, note that the column space of AB is a subspace of the column space of A. This is because the columns of AB are linear combinations of the columns of A.
Thus, the column-space dimension of AB is at most equal to the column-space dimension of A equal to rA.
Similarly, the row space of AB is a subspace of the row space of B. This is because the rows of AB are linear combinations of the rows of B.
Therefore, the row-space dimension of AB is at most equal to the row-space dimension of B equal to rB.
Now consider the null space of AB. ABx = 0 if x is a vector in the null space of AB. This means that Bx is in A's null space.
Therefore, the dimension of the nullspace of AB is at least the dimension of the nullspace of A, and by the rank zeroness theorem, the dimension of the nullspace of A is n-rA.
Therefore, the dimension of the null space of AB is at least n - rA.
Similarly, consider the null space of B. ABx = 0 if x is a vector in the null space of B. This means that Ax is in the null space of AB.
Therefore, the dimension of the null space of B is at least the dimension of the null space of AB. By the rank nullity theorem, the dimension of the null space of AB is p − rB.
Therefore, the dimension of the null space of B is at least p − rB. Combining these inequalities gives:
Disabled (AB) ≥ n - rA
invalid (AB) ≥ p - rB
Adding these inequalities gives:
2nullity(AB) ≥ (n + p) - (rA + rB)
The rank zero theorem tells us that:
Invalid (AB) = n - Rank (AB) = p - Rank (AB)
So the above inequality can be rewritten as
2(Rank(AB)) ≤ (n + p) - (rA + rB)
Adding rA + rB on both sides gives:
2(Rank(AB)) + rA + rB ≤ n + p
Since rank(AB), rA, and rB are all non-negative integers,
2(Rank(AB)) ≤ n + p
Dividing both sides by 2 gives:
rank(AB) ≤ (n + p)/2
Both n and p are non-negative integers, so
(n + p)/2 ≤ min(n, p)
For this:
rank(AB) ≤ min(n, p) = min(rank(A), rank(B))
This completes the proof.
learn more about the rank nullity theorem
brainly.com/question/30023972
#SPJ4
